кипу
Археолози разгадаха мистериозната "Лента от дупки" в Перу, разкривайки древна счетоводна система

Животът
Едноклетъчните организми имат по-сложен ДНК епигенетичен код от многоклетъчния живот

Медицина
Учени създадоха изключително реалистичен дигитален мозък на мишка

Земята
COP30: Големи обещания, малък напредък

Човекът
Най-старото известно изображение на Сътворението е върху древна сребърна чаша

Технологии
Изкуствен интелект със скоростта на светлината? Вече е възможно

Космос
Мистерията се задълбочава - изолирана галактика образува звезди без видимо гориво

Животът
Пчелите имат усещане за време: Ново проучване разкрива шокиращо напреднал интелект на насекомите
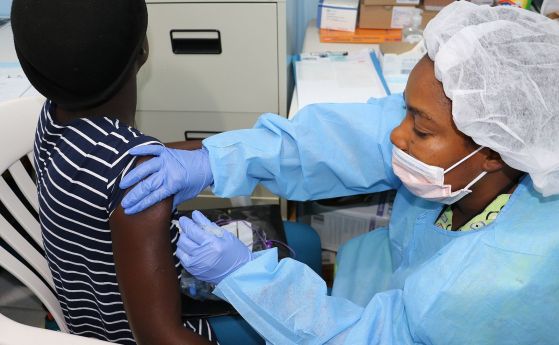
Здраве
Нова ваксина против малария дава надежда на майки и бебета в цяла Африка

Новини
Четири научни звена на БАН отварят врати за посетители

Земята
Китайски екип открива папрат, която произвежда редкоземни елементи

Животът
Нов универсален закон разкрива границите на растежа на живота

Животът
Вижте как рибата прилепало се движи на автостоп с гърбатите китове (3 видеа)

Космос
Три хиперскоростни звезди показват къде е свръхмасивната черна дупка на Големия Магеланов облак

Човекът
Нобеловата награда за икономика за 2025 г. е за обяснение на икономическия растеж, обусловен от иновациите

Космос
Засякоха първия радиосигнал от междузвездната комета 3I/ATLAS. Льоб отново каза:"извънземни!"

Космос
Да, вярно е: Вселената е била по-топла, отколкото е сега

Новини
Лекция "Нобеловите награди по физика за 2024" , водена от чл.-кор. Язаджиев и проф.Славова

Човекът
Древни геноми определят категорично два източника на индоевропейските езици

Човекът
Разбирането на съзнанието е спешно необходимо, предупреждават учени

Космос
Разширяването на Вселената сега се забавя, а не се ускорява

Космос
Секунда след Големия взрив са създадени черни дупки, бозонни звезди и звезди-канибали

Космос
Черните дупки със звездна обвивка могат да разрешат загадката на малките червени точки

Земята
COP30: Големи обещания, малък напредък

Космос
SpaceX изстреля мегаракетата Starship при успешен изпитателен полет (видео)

Животът
За първи път е регистриран вълк, използващ рибарска мрежа (видео)

Животът
Бруталната битка на шимпанзетата за територия води до бейби бум

Животът
Едноклетъчните организми имат по-сложен ДНК епигенетичен код от многоклетъчния живот

Животът
Пчелите имат усещане за време: Ново проучване разкрива шокиращо напреднал интелект на насекомите

Човекът
Трайни модели в езиците по света

Човекът
Най-старото известно изображение на Сътворението е върху древна сребърна чаша

Човекът
Как нашият аромат тайно сигнализира за социалния статус

Човекът
Математически изчезването на неандерталците се обяснява с генетично разреждане

Човекът
Археолози разгадаха мистериозната "Лента от дупки" в Перу, разкривайки древна счетоводна система

Медицина
Учени създадоха изключително реалистичен дигитален мозък на мишка

Медицина
Откриха молекула, която имитира ефекта на упражненията и забавя стареенето

Медицина
Защо пациентите с Алцхаймер забравят близките си и как може да бъде спряно това

Медицина
Медитацията пренастройва клетките на тялото според "еретично" проучване

Скептик
Южнокорейският пластир за регенериране на зъби е фалшива новина

Скептик
Загадъчни изчезващи обекти в небето, свързани с ядрени опити и НЛО (НАЯ)

Скептик
"Извънземните мумии" от Перу: Странните им пръстови отпечатъци пораждат нови съмнения

Скептик
Учени подлагат човешки клетки на огромни дози 5G - и нищо не се случва

Защо
Коя националност е най-древна?

Защо
Защо не можете да се задушите, като си задържате дъха?

Защо
Ако сме произлезли от маймуните, защо има още маймуни?

Защо
Защо домашните котки са по-малки в сравнение с големите котки?

Защо
Защо повечето бозайници имат 5 пръста?

Хумор
Мъск задължи астронавтите да се гримират като Ванс

Хумор
Стотици мечки са блокирали входа на парка Йелоустоун? Истина или лъжа?

Хумор
Научни факти, които може да ви съсипят Коледата