
„Квантовото вплитане е едно от най-изтънчените концепции в науката, но в основата му са прости принципи. Веднъж разбрано вплитането открива по-задълбочено разбиране на понятия като "множественост на световете" в квантовата теория”, пише във въведението на статията си за Quanta magazine Франк Вилчек (Frank Wilczek) - американски теоретичен физик, математик и лауреат на Нобелова награда, в момента професор по физика в Масачузетския технологичен институт.
Представяме ви неговите обяснения за едно от основните странни явления в квантовата механика, което като че ли и Айнщайн не бе разбрал.
Понятието квантово вплитане е обгърнато с очароваща мистерия и (по някакъв начин) е свързано с изискването на квантовата теория за необходимостта от "много светове".
И все пак, по същество това са научни идеи със земен смисъл и конкретни приложения. Бих искал да обясня понятията вплитане и набор от светове толкова просто и ясно, колкото ги разбирам аз.
I
Вплитането често се разглежда като уникално квантово-механично явление, но не е така. Всъщност, за начало, като по-разбираемо, макар и необичайно, ще разгледаме една проста неквантова (или "класическа") версия на вплитането. Това ни позволява да разкрием тънкостите на самото вплитане, отделно от другите странности на квантовата теория.
Вплитането възниква в ситуации, в които имаме частична информация за състоянието на две системи. Например, нашите системи могат да бъдат два обекта, които ще наречем „К-они” (c-ons). С "К" имам за цел да подскажа "класически", но ако искате да си представите нещо специфично и приятно в съзнанието си, може да мислите за нашите каони (както ще ги наричаме за благозвучие ние - бел. пр.) като за кексчета.
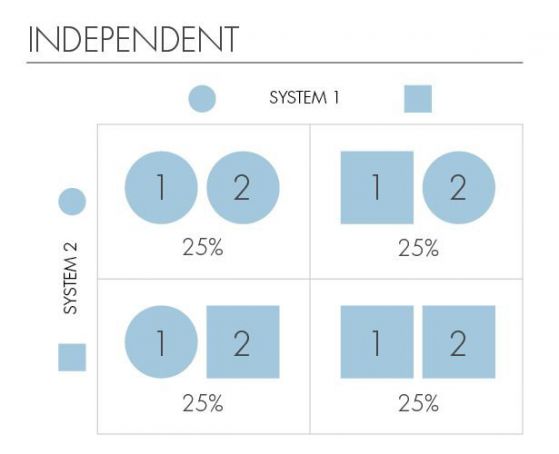
Нашите каони ще имат две форми, квадратни или кръгли, и тези форми ще показват техните възможни състояния. Четирите възможни смесени състояния на двата вида каони са: (квадрат, квадрат), (квадрат, кръг), (кръг, квадрат), (кръг, кръг). Таблицата показва вероятността системата да се намира в едно от четирите изброени състояния.
 Olena Shmahalo/Quanta Magazine
Olena Shmahalo/Quanta Magazine
Каоните са "независими", ако знанието за състоянието на единия от тях не ни дава информация за състоянието на другия. Първата таблица има това свойство. Ако първият каон (кекс) е квадрат, все още не знаем формата на втория. Обратно, формата на втория не ни казва нищо за формата на първия.
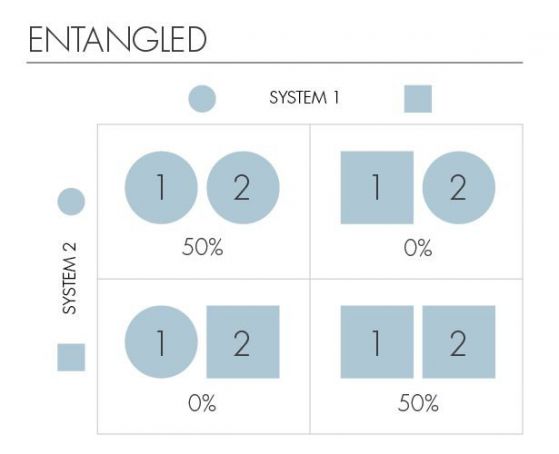
От друга страна, казват, че два каона са вплетени, ако информацията, да кажем, за единия от тях подобрява познанията ни за другия. Втората таблица ще ни покаже силно вплитане. В този случай, ако първият каон е кръг, ние ще знаем, че вторият каон също е кръгъл. И ако първият каон е квадрат, тогава вторият каон ще бъде също квадратен. Знаейки формата на единия, недвусмислено можем да определим формата на другия.
 Olena Shmahalo/Quanta Magazine
Olena Shmahalo/Quanta Magazine
Квантовата версия на вплитането е по същество същият феномен - т.е. липса на независимост. В квантовата теория състоянията се описват от математически обекти, наречени вълнови функции. Правилата, свързващи вълновите функции с физическите вероятности, въвеждат много интересни усложнения, както ще обсъдим, но основните понятия за вплетените системи, които демонстрирахме в класическия случай, остават същите.
Кексчетата не са квантови системи, разбира се, но вплитане между квантовите системи възниква по естествен начин - например, след сблъсъци на частици. На практика, невплетените (независими) състояния са по-скоро редки изключения, защото когато системите си взаимодействат, взаимодействието създава взаимовръзки между тях.
Да разгледаме например молекулите. Те се състоят от подсистеми, а именно електрони и ядра. Най-ниското енергийно състояние на молекулата, което се среща най-често, е силното вплетено състояние на нейните електрони и ядра, тъй като позициите на съставящите я частици никак не са независими. Когато ядрото се движи, електронът се движи с него.
Да се върнем към нашия пример. Ако обозначим с Φ■, Φ● вълновите функции, които описват системата 1 с нейните квадратни или кръгли състояния и ψ■, ψ● за вълновите функции, които описват системата 2 с нейните квадратни или кръгли състояния, тогава в нашия пример всички състояния могат да бъдат описани като:
Независими: Φ■ ψ■ + Φ■ ψ● + Φ● Ψ● + Φ● ψ■
Вплетени: Φ■ ψ■ + Φ● ψ●
Независимата версия може да бъде написана и като:
(Φ■ + Φ●) (ψ■ + ψ●)
Забележете, че в последния случай скобите ясно разделят независимите части на първата и втората системи.
Има много начини за създаване на вплетени състояния. Единият от тях е да се измери съставна система, която дава частична информация. Може например, че две системи са се „разбрали” да бъдат от една и съща форма, без същевременно да се знае коя форма са избрали. Тази концепция ще стане важна малко по-късно.
По-характерните последици от квантовото вплитане, като ефектите на Айнщайн-Подолски-Rosen (EPR) и Грийнбърг-Хорн-Зелингер (GHZ), възникват в резултат на взаимодействието с още една особеност на квантовата теория, наречена "принцип на допълнителността". За да обсъдим EPR и GHZ, нека първо да ви запозная с този принцип.
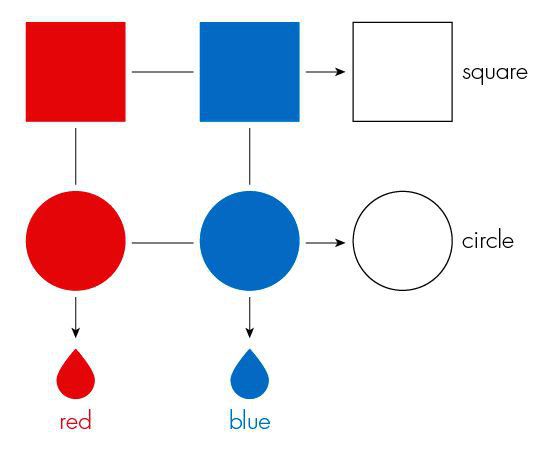
До този момент си представяхме, че каоните са в две форми (квадратни и кръгли). Сега си представете, че те са също могат да бъдат и в два цвята - червено и синьо. Разглеждайки класическата система, например, кексчетата, това допълнително свойство, ще означава, че каонът може да съществува в едно от четирите възможни състояния: червен квадрат, червен кръг, син квадрат и син кръг.
Но квантовите кексчета - кванткексчетата - или квантони (q-on) - се държат много по-различно. Фактът, че в някои ситуации даден квантон може да има различни форми и цветове, не означава непременно, че едновременно има и формата, и цвета. Всъщност, здравият смисъл, изискван от Айнщайн от физическата действителност, не съответства на експерименталните факти, които скоро ще видим.
Можем да измерим формата на квантона, но губим цялата информация за неговия цвят. Или можем да измерим цвета му, но губим информация за неговата форма. Според квантовата теория не можем едновременно да измерим и формата, и цвета. Никой не може да възприеме квантовата реалност в нейната пълнота, той трябва да вземете под внимание много различни и взаимно изключващи се картини, всяка от които дава своя собствена непълна представа за това, което се случва. Това е същността на принципа на допълнителността, такъв, какъвто бе формулиран от Нилс Бор.
В резултат на това, квантовата теория ни принуждава да бъдем внимателни при приписването на свойства на физическата реалност. За да избегнем противоречията, трябва да признаем, че:
- Няма свойство, ако не е измерено.
- Измерването е активен процес, който променя измерената система.
 Olena Shmahalo/Quanta Magazine
Olena Shmahalo/Quanta Magazine
II
Сега да опишем две популярни (класически), но не „класически” илюстрации на странностите на квантовата теория. И двете са проверени в строги експерименти (в реалните експерименти хората не измерват формите и цветовете на кексчета, а ъгловите моменти на електроните).
Алберт Айнщайн, Борис Подолски и Нейтън Розен (EPR) описват изненадващия ефект, който възниква, когато две квантови системи са вплетени. Ефектът EPR съчетава в специфична експериментално постижима форма квантовото вплитане с принципа на допълнителността.
EPR-двойката се състои от два квантона, всеки от които може да бъде измерен по форма или цвят (но не и двете едновременно). Да предположим, че имаме много такива двойки, те са еднакви и можем да изберем какви измервания ще направим на техните компоненти. Ако измерим формата на един от членовете на двойката EPR, вероятно ще получим квадрат или кръг. Ако измерим цвета, тогава с еднаква вероятност получаваме червено или синьо.
Интересните ефекти на EPR, смятани за парадоксални, възникват, когато правим измервания и на двата члена на двойката. Когато измерваме цвета на двата члена или тяхната форма, установяваме, че резултатите винаги съвпадат. Тоест, ако установим, че единият от тях е червен и след това измерим цвета на втория, откриваме, че е също червен - и т.н. От друга страна, ако измерим формата на единия и цвета на другия, не се наблюдава корелация. Тоест, ако първият е квадрат, тогава вторият с една и съща вероятност може да бъде син или червен.
Според квантовата теория ще получим същите резултати, дори ако двете системи са разделени от огромно разстояние и измерванията са направени почти едновременно. Изборът на типа измерване на едното място очевидно оказва влияние върху състоянието на системата на другото. Това "призрачно действие на разстояние", както го нарече Айнщайн, очевидно изисква предаване на информация - в нашия случай информацията за измерването - със скорост, надхвърляща скоростта на светлината.
Но дали е така? Докато аз не разбера какъв резултат имаш ти, не знам какво да очаквам за мен. Получавам полезна информация, когато разбера твоя резултат, а не когато ти измерваш. И всяко съобщение, съдържащо твоя резултат, трябва да бъде предадено по някакъв физически начин, по-бавно от скоростта на светлината.
Но ако вникнем още, парадоксът започва да се размива. Нека да разгледаме състоянието на втората система, ако измерването на първата даде червен цвят. Ако решим да измерим цвета на втория квантон, той ще бъде червен. Но съгласно принципа на допълнителността, ако решим да измерим формата му, когато е в "червено" състояние, ще имаме еднаква вероятност да получим квадрат или кръг. Следователно резултатът от EPR е логически предварително определен. Това е просто принципът на допълнителността в друга опаковка.

Няма парадокс във факта, че са свързани отдалечени събития. В края на краищата, ако сложим по една от много чифтове ръкавици в кутии и ги изпратим в различни краища на света, не е чудно, че поглеждайки в едната кутия, мога да определя за коя ръка е предназначена другата ръкавица. По същия начин във всички случаи корелацията на ЕРР двойките трябва да бъде фиксирана, когато са близо една до друга и така могат да издържат на последващото разделяне, сякаш имат памет. Странността на парадокса EPR не е в корелацията като такава, а във възможността за нейното запазване във вид на допълващи се форми.
III
Даниел Грийнбъргър (Daniel Greenberger), Майкъл Хорн (Michael Horne) и Антон Зелингър (Anton Zeilinger) откриват още един блестящ пример за квантово вплитане. Той включва три от нашите квантони, които са в специално подготвено вплетено състояние (GHZ-състояние). Разпределяме всеки един от тях на различни отдалечени експериментатори. Всеки от тях избира самостоятелно и случайно дали да измерва цвят или форма и записва резултата. Експериментът се повтаря многократно, но винаги трите квантона започват в състояние GHZ.
Всеки отделен експериментатор получава произволни резултати. При измерването на формата на квантона е еднакво вероятно да получи квадрат или кръг. Измерването на цвета на квантона е също толкова вероятно да даде червено или синьо. До тук всичко е както обикновенно.
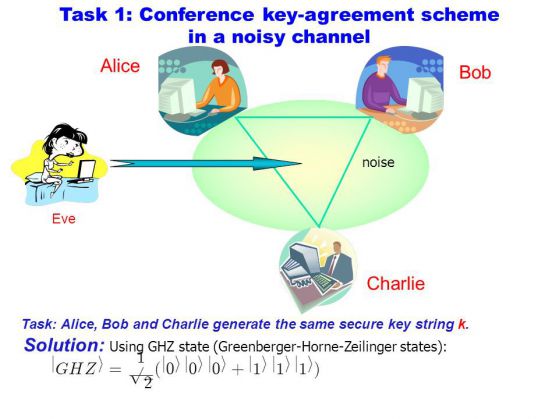
Но когато експериментаторите се събират и сравняват резултатите, анализът показва невероятен резултат. Да наречем тези с квадратна форма и червен цвят "добри", а тези с кръгчетата и син цвят - "зли". Експериментаторите установявяват, че ако двама от тях са решили да измерят формата, а трети - цвета, тогава 0 или 2 резултати от измерванията ще се получат "зли" (т.е., кръгли или сини). Но ако и тримата решат да измерят цвета, тогава 1 или 3 измервания се оказват зли. Това се прогнозира от квантовата механика, и точно това се случва.
Въпрос: Дали количеството на злото е четно или нечетно? В различни измервания се реализират и двете възможности. Трябва да изоставим този въпрос. Няма смисъл да се говори за количеството на злото в една система, без да се взема предвид как се измерва. И това води до противоречия.
Ефектът GHZ, както е описан от физика Сидни Колман (Sidney Coleman), е "шамар от квантовата механика". Той унищожава обичайното очакване, получено от нашия опит, че физическите системи имат предварително определени свойства, независимо от тяхното измерване. Ако това бе така, тогава балансът на доброто и злото нямаше да зависи от избора на типовете измервания. След като приемем съществуването на ефекта GHZ, няма да го забравим и ще се разшири начина ни на мислене.
IV
Досега обсъждахме как вплитането не ни позволява да присвоим уникални независими състояния на няколко квантона. Същата логика е приложима и за промените в един квантон, възникващи във времето.
Говорим за "вплетени истории" (вплитания във времето), когато на системата не може да се присвои определено състояние по което и да е време. Подобно на начина, по който се стига до конвенционалното вплитане, изключвайки някои възможности, можем да създаваме темпорални вплитения като извършваме измервания, събиращи частична информация за минали събития.
В най-простите истории на вплитане имаме един квантон, изучаван от нас в две различни времеви точки. Можем да си представим ситуация, в която установяваме, че формата на нашия квантон е веднъж квадратна, а после кръгла, като и двете ситуации остават възможни. Това е времева квантова аналогия с по-простите варианти на вплитане (в пространството - бел. пр.), описани по-горе.

С помощта на по-сложни споразумения (протокол), можем да добавим малко допълнителност в тази система, както и да дефинираме ситуации, които водят до свойството "множественост на световете" в квантовата теория. Нашият квантон може да се подготви в червено състояние, след което да се измери и да се получи в синьо състояние. И както в предишните примери, както не можем на квантон трайно да присвоим свойството цвят в интервала между две измерения, така той няма определена форма. Такива истории ни карат да осъзнаем по един ограничен, но напълно контролируем и точен начин интуицията, която лежи в основата на свойствената на квантовата механика множественост на световете картина. Едно определено състояние може да бъде разделено на две противоречащи си една на друга исторически траектории, които след това отново да се свържат.
Ървин Шрьодингер, основателят на квантовата теория, е скептичен относно истинността на тази картина, подчертавайки, че еволюцията на квантовите системи естествено води до състояния, чието измерване може да даде изключително различни резултати. Неговият мислен експеримент с "котката на Шрьодингер" постулира, както знаем, квантовата неопределеност, изведена на ниво влияние върху смъртността на котките. Преди измерването на котката не може да ѝ бъде приписано свойството живот (или смърт). И двете състояния - или нито едното от тях - съществуват заедно в други светове на възможности.
Езикът, който използваме в ежедневието си, е неподходящ, за да обясни квантовата допълнителност, тъй като тя липсва във всекидневния ни опит. Практически котките взаимодействат с околните въздушни молекули, както и с други предмети по съвсем различни начини, които зависят от това дали са живи или мъртви, така че на практика измерването се стартира автоматично, а котката остава стабилно в едно от двете състояния - жива (или мъртва). Но историята на вплитането описва квантони, които са Шрьодингерерови котета. Пълното им описание изисква да вземем предвид две взаимно изключващи се траектории на свойства.
Контролираната експериментална реализация на истории на вплитане (времево вплитане - бел. пр.) е деликатен въпрос, тъй като изисква събирането на частична информация за квантоните. Конвенционалните квантови измервания обикновено събират цялата информация наведнъж - например определят точната форма или точния цвят - вместо да получават частична информация. Но това може да се направи, макар и с изключителни технически трудности. По този начин можем да зададем определен математически и експериментален смисъл на концепцията за "множественост на световете" в квантовата теория и да демонстрираме нейната реалност.
Още по темата

Физика
Квантови странности в парадокса "кокошката или яйцето"

Физика
Физици счупиха квантов рекорд, като се впуснаха на ново призрачно ниво
Физика
На тази дата Нилс Бор завършва статията си, която полага началото на квантовата теория




















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Доколко съвместими са минерално-суровинният отрасъл и чистата околна среда?
Козон
Мистериозен череп на гръцки хоминин е датиран на поне 286 000 години
Peter Petrov
След многократни експлозии нов тест за мегаракетата на Мъск
поп Дръвчо
Гледайте за първи път на живо как новооткритият "междузвезден посетител" 3I/ATLAS се устремява към нас