

–Т—К–≤–µ–і–µ–љ–Є–µ
–®–Є—А–Њ–Ї–Њ—В–Њ –њ—А–Є–ї–Њ–ґ–µ–љ–Є–µ –љ–∞ –Љ–µ—В–Њ–і–Є—В–µ –љ–∞ —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ –Ј–∞–њ–Њ—З–љ–∞–ї–Њ —Б–ї–µ–і –Є–Ј–ї–Є–Ј–∞–љ–µ—В–Њ –љ–∞ –Ї–љ–Є–≥–∞—В–∞ –љ–∞ –µ–і–Є–љ –Њ—В —Б—К–Ј–і–∞—В–µ–ї–Є—В–µ –љ–∞ —В–∞–Ј–Є —В–µ–Њ—А–Є—П вАФ –†–µ–љ–µ –Ґ–Њ–Љ (Ren√© Thom), –Ї—К–і–µ—В–Њ —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ –±–Є–ї–∞ –њ—А–Є–ї–Њ–ґ–µ–љ–∞ –Ј–∞ –Є–Ј—Г—З–∞–≤–∞–љ–µ –љ–∞ –Љ–Њ—А—Д–Њ–≥–µ–љ–µ–Ј–∞—В–∞ (—Д–Њ—А–Љ–Њ–Њ–±—А–∞–Ј—Г–≤–∞–љ–µ—В–Њ) –≤ –±–Є–Њ–ї–Њ–≥–Є—П—В–∞.
Teo—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ —Б—В–∞–≤–∞ –њ–Њ–њ—Г–ї—П—А–љ–∞ –Њ—В 1970–≥, –Ї–Њ–≥–∞—В–Њ –≤ —Б–њ–Є—Б–∞–љ–Є–µ "–Э—О–Ј—Г–Є–Ї" —Б–µ —Б—К–Њ–±—Й–∞–≤–∞ –Ј–∞ –њ—А–µ–≤—А–∞—В–∞ –≤ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞, —Б—А–∞–≤–љ–Є–Љ —Б–∞–Љ–Њ —Б –Є–Ј–Њ–±—А–µ—В–µ–љ–Њ—В–Њ –Њ—В –Э—О—В–Њ–љ –і–Є—Д–µ—А–µ–љ—Ж–Є–∞–ї–љ–Њ –Є –Є–љ—В–µ–≥—А–∞–ї–љ–Њ —Б–Љ—П—В–∞–љ–µ. –Ґ–≤—К—А–і—П–ї–Њ —Б–µ, —З–µ –і–Њ–Ї–∞—В–Њ –љ—О—В–Њ–љ–Њ–≤—Б–Ї–∞—В–∞ —В–µ–Њ—А–Є—П –Є–Ј—Б–ї–µ–і–≤–∞ —Б–∞–Љ–Њ –њ–ї–∞–≤–љ–Є, –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Є –њ—А–Њ—Ж–µ—Б–Є, –љ–Њ–≤–∞—В–∞ –љ–∞—Г–Ї–∞-—Вeo—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ –і–∞–≤–∞ —Г–љ–Є–≤–µ—А—Б–∞–ї–µ–љ –Љ–µ—В–Њ–і –Ј–∞ –Є–Ј—Б–ї–µ–і–≤–∞–љ–µ –љ–∞ –≤—Б–Є—З–Ї–Є —Б–Ї–Њ–Ї–Њ–Њ–±—А–∞–Ј–љ–Є –њ—А–µ—Е–Њ–і–Є, —А–∞–Ј—А–Є–≤–Є –Є –≤–љ–µ–Ј–∞–њ–љ–Є –Ї–∞—З–µ—Б—В–≤–µ–љ–Є –Є–Ј–Љ–µ–љ–µ–љ–Є—П.
–Ш–Ј–≤–Њ–і–Є—В–µ –Њ—В —Вeo—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ –Ј–∞–њ–Њ—З–≤–∞—В –і–∞ —Б–µ –њ—А–Є–ї–∞–≥–∞—В –≤ —В–Њ–ї–Ї–Њ–≤–∞ —А–∞–Ј–љ–Њ–Њ–±—А–∞–Ј–љ–Є –Њ–±–µ–Ї—В–Є –Ї–∞—В–Њ –љ–∞–њ—А–Є–Љ–µ—А, –Є–Ј—Б–ї–µ–і–≤–∞–љ–Є—П –љ–∞ —Б—К—А–і–µ—З–љ–Є—П —А–Є—В—К–Љ, –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–∞ –Є —Д–Є–Ј–Є—З–µ—Б–Ї–∞ –Њ–њ—В–Є–Ї–∞, –Є–Ї–Њ–љ–Њ–Љ–Є–Ї–∞, —Е–Є–і—А–Њ–і–Є–љ–∞–Љ–Є–Ї–∞, –≥–µ–Њ–ї–Њ–≥–Є—П –Є —В–µ–Њ—А–Є—П –љ–∞ –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–Є—В–µ —З–∞—Б—В–Є—Ж–Є, –ї–Є–љ–≥–≤–Є—Б—В–Є–Ї–∞, –Љ–Њ–і–µ–ї–Є—А–∞–љ–µ –і–µ–є–љ–Њ—Б—В—В–∞ –љ–∞ –Љ–Њ–Ј—К–Ї–∞, —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –љ–∞ –њ–ї–∞–≤–∞—В–µ–ї–љ–Є —Б—К–і–Њ–≤–µ –Є –і–Њ—А–Є –±—Г–љ—В–Њ–≤–µ –љ–∞ –Ј–∞—В–≤–Њ—А–љ–Є—Ж–Є.
–Э–∞ —А–∞–Ј–≤–Є—В–Є–µ—В–Њ –љ–∞ –≤—Б—П–Ї–∞ –і–Є–љ–∞–Љ–Є—З–љ–∞ —Б–Є—Б—В–µ–Љ–∞ —Б–∞ –њ—А–Є—Б—К—Й–Є –±–Є—Д—Г—А–Ї–∞—Ж–Є–Є—В–µ(—А–∞–Ј–і–≤–Њ–µ–љ–Є–µ –љ–∞ –њ—К—В–Є—Й–∞—В–∞ –љ–∞ –µ–≤–Њ–ї—О—Ж–Є—П—В–∞) –Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ. –С–Є—Д—Г—А–Ї–∞—Ж–Є–Є—В–µ —Б–∞ –Є–љ—В–µ—А–µ—Б–љ–Є —Б —В–Њ–≤–∞, —З–µ –љ–µ —Б—К—Й–µ—Б—В–≤—Г–≤–∞—В –њ–Њ–µ–і–Є–љ–Є—З–љ–Њ - —В–µ –њ–Њ—А–∞–ґ–і–∞—В —Ж–Є–Ї–ї–Є, —В.–µ. –±–Є—Д—Г—А–Ї–∞—Ж–Є–Є –≤ –љ–Њ–≤–Њ —Д–∞–Ј–Њ–≤–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ.
–Ъ–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ —Б–∞ –љ–µ–Є–Ј–±–µ–ґ–љ–Є. –Я—А–Є —В–Њ–≤–∞, –∞–Ї–Њ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ –Њ—В –њ–Њ-–љ–Є—Б—К–Ї –њ–Њ—А—П–і—К–Ї –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Њ –Є–Љ–∞—В –≤–Є–і –љ–∞ –≥—К–љ–Ї–∞, —В–Њ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ –Њ—В –њ–Њ-–≤–Є—Б—И –њ–Њ—А—П–і—К–Ї —Б–∞ —Б –њ–Њ-—Б–ї–Њ–ґ–љ–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–∞ —Д–Њ—А–Љ–∞ - —В–µ –љ–∞–њ–Њ–Љ–љ—П—В —Б–Є–ї–љ–Њ —Б–Љ–∞—З–Ї–∞–љ–∞ —Е–∞—А—В–Є—П. –Р–Ї–Њ —Б–µ —А–∞–Ј—А–µ–ґ–∞—В –њ–Њ –≤—А–µ–Љ–µ –Є–Љ–∞—В –≤–Є–і –љ–∞ —Б–ї–Њ–ґ–µ–љ –Ї–≤–∞–Ј–Є–њ–µ—А–Є–Њ–і–Є—З–µ–љ –њ—А–Њ—Ж–µ—Б. –Т—К–њ—А–Њ—Б—К—В –µ, –Ї—К–і–µ –≤–Њ–і–Є —В–Њ–є. –°—К–≥–ї–∞—Б–љ–Њ —А–∞–±–Њ—В–∞—В–∞ –љ–∞ –Ь.–§–µ–є–≥–µ–љ–±–∞—Г–Љ, –≤–µ–і–љ—К–ґ –≤—К–Ј–љ–Є–Ї–љ–∞–ї–Є –≤ –љ–µ–ї–Є–љ–µ–є–љ–∞ —Б–Є—Б—В–µ–Љ–∞, –±–Є—Д—Г—А–Ї–∞—Ж–Є–Є—В–µ¬†–Є–Љ–∞—В —В–µ–љ–і–µ–љ—Ж–Є—П –љ–µ–Њ–≥—А–∞–љ–Є—З–µ–љ–Њ –і–∞ —А–∞—Б—В–∞—В, –і–Њ–Ї–∞—В–Њ –љ–µ –њ—А–Є–≤–µ–і–∞—В —Б–Є—Б—В–µ–Љ–∞—В–∞ –і–Њ —Б—К—Б—В–Њ—П–љ–Є–µ –љ–∞ –њ—К–ї–µ–љ —Е–∞–Њ—Б.
–Ф–∞ —Б–µ –Ј–∞–њ–Њ–Ј–љ–∞–µ–Љ —Б –љ—П–Ї–Њ–ї–Ї–Њ –Њ—Б–љ–Њ–≤–љ–Є –њ–Њ–љ—П—В–Є—П –Њ—В —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ:
–Р—Б–Є–Љ–њ—В–Њ—В–Є—З–љ–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В
–Р—Б–Є–Љ–њ—В–Њ—В–Є—З–љ–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –Є–Љ–∞—В —Б–Є—Б—В–µ–Љ–Є, –Ї–Њ–Є—В–Њ —Б–∞ –њ—А–Є–≤–ї–µ—З–µ–љ–Є –Њ—В –љ—П–Ї–∞–Ї–≤–Њ –њ—А–µ–і–њ–Њ—З–Є—В–∞–љ–Њ —Б—К—Б—В–Њ—П–љ–Є–µ: –њ–Њ–і–Њ–±–љ–Њ –љ–∞ —В–Њ–њ—З–µ, —В—К—А–Ї–∞–ї—П—Й–Њ —Б–µ –Ї—К–Љ –љ–∞–є-–љ–Є—Б–Ї–∞—В–∞ —В–Њ—З–Ї–∞ –≤ —З–∞—И–∞ –Є–ї–Є –≤—К–Ј—Б—В–∞–љ–Њ–≤—П–≤–∞–љ–µ—В–Њ –љ–∞ –Ї–∞–Ї—К–≤—В–Њ –Є –і–∞ –µ —Е–Њ–Љ–µ–Њ—Б—В–∞–Ј–Є—Б –Њ—В —Д–Є–Ј–Є–Њ–ї–Њ–≥–Є—З–µ—Б–Ї–Є—В–µ —Б–≤–Њ–є—Б—В–≤–∞ –њ–Њ–і–Њ–±–љ–Њ —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞—В–∞ –љ–∞ —В—П–ї–Њ—В–Њ.
–•–Њ–Љ–µ–Њ—Б—В–∞–Ј–Є—Б:
 ¬†–Ш–ї—О—Б—В—А–∞—Ж–Є—П:¬†Biology 466 ¬†–Ш–ї—О—Б—В—А–∞—Ж–Є—П:¬†Biology 466 |
–Ц–Є–≤–Њ—В–љ–Є—В–µ (–Є —А–∞—Б—В–µ–љ–Є—П—В–∞) –Є–Љ–∞—В –Љ–љ–Њ–≥–Њ —Д–Є–Ј–Є–Њ–ї–Њ–≥–Є—З–љ–Є –Љ–µ—Е–∞–љ–Є–Ј–Љ–Є, –Ї–Њ–Є—В–Њ —Б–∞ —Б –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї–љ–Њ –њ–Њ—Б—В–Њ—П–љ–љ–∞ —Б—В–Њ–є–љ–Њ—Б—В –Ї–∞—В–Њ —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞ –љ–∞ —В—П–ї–Њ—В–Њ, pH –љ–∞ –Ї—А—К–≤—В–∞ , –Ї–Њ–љ—Ж–µ–љ—В—А–∞—Ж–Є—П –љ–∞ —Б–Њ–ї—В–∞, –Є —В.–љ. |
–Ґ–µ—Е–љ–Є—П—В –Њ—Б–љ–Њ–≤–µ–љ –њ—А–Є–љ—Ж–Є–њ –љ–∞ —Д—Г–љ–Ї—Ж–Є–Њ–љ–Є—А–∞–љ–µ –µ, —З–µ –љ–∞ –Є–Ј–Љ–µ–љ–µ–љ–Є—П—В–∞ —Б–µ –њ—А–Њ—В–Є–≤–Њ–њ–Њ—Б—В–∞–≤—П—В –і–≤–Њ–є–Ї–∞ –Љ–µ—Е–∞–љ–Є–Ј–Љ–Є, –Ї–Њ–Є—В–Њ —Г–њ—А–∞–≤–ї—П–≤–∞—В –Є –±–∞–ї–∞–љ—Б–Є—А–∞—В –≤ –ґ–µ–ї–∞–љ–Є –≥—А–∞–љ–Є—Ж–Є –Є–Ј–Љ–µ–љ—П—Й–Є—В–µ —Б–µ —Д—Г–љ–Ї—Ж–Є–Є –њ–Њ–і–Њ–±–љ–Є –љ–∞ —В–µ–Љ–њ–µ—А–∞—В—Г—А–∞—В–∞.
–Р—В—А–∞–Ї—В–Њ—А–µ–љ –±–∞—Б–µ–є–љ:
| –Р—В—А–∞–Ї—В–Њ—А–µ–љ–Є—П—В –±–∞—Б–µ–є–љ –Є–Љ–∞ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ —Б–∞–Љ–Њ –Њ–≥—А–∞–љ–Є—З–µ–љ–∞ –Њ–±–ї–∞—Б—В –Њ—В —Б—В–Њ–є–љ–Њ—Б—В–Є –љ–∞ —Б—В–∞–±–Є–ї–љ–Є –њ—А–Њ–Љ–µ–љ–ї–Є–≤–Є, –Ї—К–Љ –Ї–Њ–Є—В–Њ —Б–Є—Б—В–µ–Љ–∞—В–∞ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –њ—А–Є–≤–ї–µ—З–µ–љ–∞ –Њ–±—А–∞—В–љ–Њ –≤ —Б–≤–Њ–µ—В–Њ –њ—А–µ–і–њ–Њ—З–Є—В–∞–љ–Њ —Б—К—Б—В–Њ—П–љ–Є–µ; —В–Њ–≤–∞ –µ –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ –љ–∞ –≥—А–∞–љ–Є—Ж–Є—В–µ –љ–∞ –і–Њ–ї–Є–љ–∞; –Ј–∞–і —Е—А–µ–±–µ—В–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ —Б–µ —Г–≤–ї–Є—З–∞ –≤ –і—А—Г–≥–Є –±–∞—Б–µ–є–љ–Є. –°–Љ—К—А—В—В–∞ –љ–∞—Б—В—К–њ–≤–∞, –Ї–Њ–≥–∞—В–Њ —Б–µ –Њ–Ї–∞–ґ–µ—В–µ –Ј–∞–і –њ—А–µ–і–µ–ї–Є—В–µ –љ–∞ —Е–Њ–Љ–µ–Њ—Б—В–∞—В–Є—З–љ–Є—В–µ –±–∞—Б–µ–є–љ–Є! | 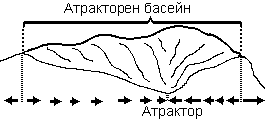 ¬†–Ш–ї—О—Б—В—А–∞—Ж–Є—П:¬†Biology 466 ¬†–Ш–ї—О—Б—В—А–∞—Ж–Є—П:¬†Biology 466 |
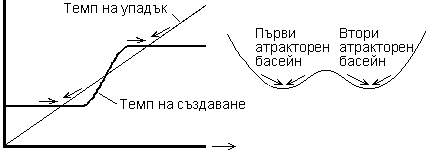
–°—В—А—Г–Ї—В—Г—А–љ–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В:–Ъ–Њ–≥–∞—В–Њ –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–љ–∞—В–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ —Б–µ –Ј–∞–і—К—А–ґ–∞ –і–∞–ґ–µ –∞–Ї–Њ –њ—А–Њ–Љ–µ–љ–Є—В–µ —Б–∞ —Б—К—Й–µ—Б—В–≤–µ–љ–Є, —В.–µ. —Б—К—Б—В–Њ—П–љ–Є–µ—В–Њ –љ–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –Є–Љ–∞ —В–Є–њ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –њ–Њ-–≤–Є—Б—И –њ–Њ—А—П–і—К–Ї. –Ф—Г–Љ–∞—В–∞ "—Б—В—А—Г–Ї—В—Г—А–µ–љ" —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞ –≤ —Б–Љ–Є—Б—К–ї –љ–∞ –њ—А–Є—Б—К—Й, –≤—А–Њ–і–µ–љ. |
 ¬†–Ш–ї—О—Б—В—А–∞—Ж–Є—П:¬†Biology 466
¬†–Ш–ї—О—Б—В—А–∞—Ж–Є—П:¬†Biology 466
–Ъ–∞—В–∞—Б—В—А–Њ—Д–Є—З–љ–∞ –≥—А—Г–њ–∞
–Ъ–∞—В–∞—Б—В—А–Њ—Д–∞—В–∞ —Б—В–∞–≤–∞ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ –≤–Є–љ–∞–≥–Є, –Ї–Њ–≥–∞—В–Њ –Є–Ј–Љ–µ–љ—П—В–µ —Г–њ—А–∞–≤–ї—П–≤–∞—Й–Є—В–µ –њ—А–Њ–Љ–µ–љ–ї–Є–≤–Є —В–∞–Ї–∞, —З–µ –≤ –Ї—А–∞–є–љ–∞ —Б–Љ–µ—В–Ї–∞ –±–∞—Б–µ–є–љ—К—В¬†–љ–∞ –∞—В—А–∞–Ї—В–Њ—А–∞ –љ–∞ —Б—В–∞—А–∞—В–∞ –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–љ–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –±—К–і–µ —Г–љ–Є—Й–Њ–ґ–µ–љ. –Ґ–Њ–≤–∞ –µ —Б—А–µ–і—Б—В–≤–Њ —Б–Є—Б—В–µ–Љ–∞—В–∞ –і–∞ –њ—А–µ—Б–Ї–Њ—З–Є –≤ –љ—П–Ї–∞–Ї–≤–Њ –љ–Њ–≤–Њ —Б—К—Б—В–Њ—П–љ–Є–µ. –°–Ї–Њ–Ї—К—В —Б–µ –љ–∞—А–Є—З–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–∞, –∞ –Ї–Њ–љ–Ї—А–µ—В–љ–Є—В–µ –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Є –≤–µ–ї–Є—З–Є–љ–Є, —Г–њ—А–∞–≤–ї—П–≤–∞—Й–Є –њ—А–Њ–Љ–µ–љ–ї–Є–≤–Є—В–µ –њ–Њ –≥—А–∞–љ–Є—Ж–∞—В–∞, –Ї—К–і–µ—В–Њ —Б–µ —А–∞–Ј–±–Є–≤–∞ –њ—А–µ–≥—А–∞–і–∞—В–∞¬†—Б–∞ –љ–∞—А–µ—З–µ–љ–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—З–љ–∞ –≥—А—Г–њ–∞ .
–°–µ–і–µ–Љ—В–µ –≤–Є–і–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є
–Ґ–µ–Њ—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –≤—Б—К—Й–љ–Њ—Б—В —В–µ–Њ—А–Є—П –љ–∞ —Б—В—А—Г–Ї—В—Г—А–љ–∞—В–∞ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –љ–∞ —Б–њ–µ—Ж–Є–∞–ї–µ–љ –Ї–ї–∞—Б –і–Є—Д–µ—А–µ–љ—Ж–Є–∞–ї–љ–Є —Г—А–∞–≤–љ–µ–љ–Є—П —Б –њ—А–Њ–Є–Ј–≤–Њ–ї–µ–љ –±—А–Њ–є —Д–∞–Ј–Њ–≤–Є –њ—А–Њ–Љ–µ–љ–ї–Є–≤–Є, –Ї–Њ–≥–∞—В–Њ –і—П—Б–љ–∞—В–∞ —З–∞—Б—В –љ–∞ —В–µ–Ј–Є —Г—А–∞–≤–љ–µ–љ–Є—П –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –њ—А–µ–і—Б—В–∞–≤–µ–љ–∞ –≤—К–≤ –≤–Є–і –љ–∞ –≥—А–∞–і–Є–µ–љ—В–љ–∞ —Б–Є—Б—В–µ–Љ–∞, —В. –µ. –Ї–∞—В–Њ –і–≤–Є–ґ–µ–љ–Є–µ –≤ –њ–Њ–ї–µ –љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–љ–Є —Б–Є–ї–Є —Б –њ–Њ—В–µ–љ—Ж–Є–∞–ї F:
–Я–∞—А–∞–Љ–µ—В—А–Є –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–∞—В–∞
–Ъ–ї—О—З –Ј–∞ —А–∞–Ј–±–Є—А–∞–љ–µ—В–Њ –љ–∞ —Вeo—А–Є—П—В–∞ –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ, –µ –µ–і–Є–љ –Њ—В —Б–µ–і–µ–Љ—В–µ –Љ–Њ–і–µ–ї–∞, –љ–∞—А–µ—З–µ–љ "–≤–Є—В–ї–Њ" –љ–∞ –£–Є—В–љ–Є. –Ґ–∞–Ј–Є –њ–Њ–≤—К—А—Е–љ–Њ—Б—В, –Њ–њ–Є—Б–≤–∞—Й–∞ —Б—К—Б—В–Њ—П–љ–Є–µ—В–Њ –љ–∞ –љ–µ–ї–Є–љ–µ–є–љ–Є —Б–Є—Б—В–µ–Љ–Є, –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –љ–µ—Й–Њ –Ї–∞—В–Њ –Ї–∞—А—В–∞, –Ї–Њ—П—В–Њ –њ–Њ–Ј–≤–Њ–ї—П–≤–∞ –і–∞ —Б–µ –Њ—А–Є–µ–љ—В–Є—А–∞–Љ–µ –≤ –њ–Њ–≤–µ–і–µ–љ–Є–µ—В–Њ –љ–∞ –Њ–±–µ–Ї—В–∞
|
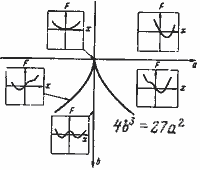
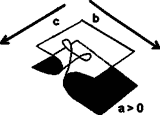
–Я–Њ–≤–µ–і–µ–љ–Є–µ—В–Њ –љ–∞ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–љ–∞—В–∞ —Д—Г–љ–Ї—Ж–Є—П: ¬†F (x, a, b) = x4/4 - bx2/2 –Ј–∞ —А–µ–∞–ї–љ–Є —Е –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В –Њ—В –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –∞ –Є b –µ –њ–Њ–Ї–∞–Ј–∞–љ–Њ –≤–і—П—Б–љ–Њ. –Р–Ї–Њ –Њ—В–ї–Њ–ґ–Є–Љ –≤ —В—А–Є–Љ–µ—А–љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –њ–Њ –≤–µ—А—В–Є–Ї–∞–ї–љ–∞—В–∞ –Њ—Б –њ–Њ–ї–Њ–ґ–µ–љ–Є–µ—В–Њ –љ–∞ —Е —А–µ–∞–ї–љ–Є—В–µ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Є —В–Њ—З–Ї–Є, –∞ –њ–Њ –і–≤–µ—В–µ –і—А—Г–≥–Є –Њ—Б–Є вАФ —Б—В–Њ–є–љ–Њ—Б—В–Є—В–µ –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –∞ –Є b, —Й–µ –њ–Њ–ї—Г—З–Є–Љ –і–Њ–ї–љ–∞—В–∞ –Ї–∞—А—В–Є–љ–Ї–∞. |
 |
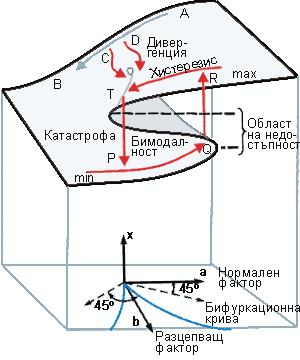 |
–Т —В–Њ—З–Ї–Є—В–µ –Њ—В –њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞, –Ї—К–і–µ—В–Њ –Є–Љ–∞ –≤–µ—А—В–Є–Ї–∞–ї–љ–∞ –і–Њ–њ–Є—А–∞—В–µ–ї–љ–∞, —З—А–µ–Ј –Њ–±—А–∞–Ј—Г–≤–∞–љ–µ –љ–∞ —В–Њ—З–Ї–Є –љ–∞ –њ—А–µ–≥—К–≤–∞–љ–µ —Б—В–∞–≤–∞ —Б–ї–Є–≤–∞–љ–µ –љ–∞ –і–≤–∞ —Б—В–∞—Ж–Є–Њ–љ–∞—А–љ–Є —А–µ–ґ–Є–Љ–∞, —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞—Й–Є –љ–∞ —В–µ—Е–љ–Є—П –Љ–Є–љ–Є–Љ—Г–Љ –Є –Љ–∞–Ї—Б–Є–Љ—Г–Љ F{x, –∞, b}. T—П—Е–љ–∞—В–∞ –њ—А–Њ–µ–Ї—Ж–Є—П –љ–∞ —А–∞–≤–љ–Є–љ–∞—В–∞ –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –∞, b –і–∞–≤–∞ –±–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ–∞—В–∞ –Ї—А–Є–≤–∞. –Я–∞—А–∞–Љ–µ—В—К—А—К—В –∞ —Б–µ –љ–∞—А–Є—З–∞ –љ–Њ—А–Љ–∞–ї–µ–љ —Д–∞–Ї—В–Њ—А, –њ–∞—А–∞–Љ–µ—В—К—А—К—В b вАФ —А–∞–Ј—Ж–µ–њ–≤–∞—Й —Д–∞–Ї—В–Њ—А, –Ј–∞—Й–Њ—В–Њ –њ—А–Є b>0 –њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞ –љ–∞ –њ–Њ–≤–µ–і–µ–љ–Є–µ —Б–µ —А–∞–Ј—Ж–µ–њ–≤–∞ –љ–∞ –і–≤–∞ –ї–Є—Б—В–∞. –Ю—Б–Є—В–µ (a ,b ), –Ј–∞–≤—К—А—В—П–љ–Є –љ–∞ 45¬∞ –≤ —А–∞–≤–љ–Є–љ–∞—В–∞ –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ, —Б–µ –љ–∞—А–Є—З–∞—В –Ї–Њ–љ—Д–ї–Є–Ї—В–љ–Є (–њ—Г–љ–Ї—В–Є—А–∞). –Ґ–∞–Ј–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–∞ –Є–Љ–∞ –њ–µ—В –Ї–∞—З–µ—Б—В–≤–µ–љ–Є –Њ—Б–Њ–±–µ–љ–Њ—Б—В–Є, –Ї–Њ–Є—В–Њ —И–Є—А–Њ–Ї–Њ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В –њ—А–Є –Љ–Њ–і–µ–ї–Є—А–∞–љ–µ –љ–∞ —А–∞–Ј–ї–Є—З–љ–Є —П–≤–ї–µ–љ–Є—П: |
- –С–Є–Љ–Њ–і–∞–ї–љ–Њ—Б—В. –Т –Њ–±–ї–∞—Б—В—В–∞, –ї–µ–ґ–∞—Й–∞ –≤—К—В—А–µ –≤ –±–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–∞—В–∞ –Ї—А–Є–≤–∞, —Б–Є—Б—В–µ–Љ–∞—В–∞ –њ—А–Є –µ–і–љ–Є –Є —Б—К—Й–Є —Б—В–Њ–є–љ–Њ—Б—В–Є –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –љ–∞–Љ–Є—А–∞ –≤ –і–≤–µ —А–∞–Ј–ї–Є—З–љ–Є —Б—К—Б—В–Њ—П–љ–Є—П (–Є–ї–Є –≤ –µ–і–љ–Њ—В–Њ, –Є–ї–Є –≤ –і—А—Г–≥–Њ—В–Њ).
- –Ю–±–ї–∞—Б—В –љ–∞ –љ–µ–і–Њ—Б—В—К–њ–љ–Њ—Б—В. –Э–∞ –Њ—Б—В–∞ –љ–∞ —Б—К—Б—В–Њ—П–љ–Є—П—В–∞ —Е —Б—К—Й–µ—Б—В–≤—Г–≤–∞ –Њ–±–ї–∞—Б—В, –≤—К—В—А–µ –≤ –Ї–Њ—П—В–Њ —Б–Є—Б—В–µ–Љ–∞—В–∞ –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –љ–∞–Љ–Є—А–∞ –њ—А–Є –љ–Є–Ї–∞–Ї–≤–Є –Ј–љ–∞—З–µ–љ–Є—П –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –≤—К—В—А–µ –≤ –±–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ–∞—В–∞ –Њ–±–ї–∞—Б—В.
- –Ъ–∞—В–∞—Б—В—А–Њ—Д–∞ (—А—П–Ј—К–Ї —Б–Ї–Њ–Ї). –Я—А–Є –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –µ –≤—К–Ј–Љ–Њ–ґ–µ–љ —А—П–Ј—К–Ї –њ—А–µ—Е–Њ–і –Њ—В –µ–і–љ–Њ —Б—К—Б—В–Њ—П–љ–Є–µ –≤ –і—А—Г–≥–Њ.
- –•–Є—Б—В–µ—А–µ–Ј–Є—Б. –†—П–Ј–Ї–Њ—В–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –≤ –њ–Њ–≤–µ–і–µ–љ–Є–µ—В–Њ –Ј–∞–≤–Є—Б–Є –Њ—В –њ—А–µ–і–Є—Б—В–Њ—А–Є—П—В–∞ –љ–∞ –њ—А–Њ—Ж–µ—Б–∞. –Э–∞–њ—А–Є–Љ–µ—А, –∞–Ї–Њ —Б—К—Б—В–Њ—П–љ–Є–µ—В–Њ –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Њ —Б–µ –Є–Ј–Љ–µ–љ—П –њ–Њ –Ї—А–Є–≤–∞—В–∞ PQ, —В–Њ —Б–Ї–Њ–Ї—К—В –Њ—В –і–Њ–ї–љ–Є—П –ї–Є—Б—В –љ–∞ –≥–Њ—А–љ–Є—П —Й–µ —Б—В–∞–љ–µ –Њ—В —В–Њ—З–Ї–∞ Q –≤ —В–Њ—З–Ї–∞ –†. –Р–Ї–Њ —В–Њ–≤–∞ —Б—К—Б—В–Њ—П–љ–Є–µ —Б–µ –Є–Ј–Љ–µ–љ—П –њ–Њ –Ї—А–Є–≤–∞—В–∞ RT,—В–Њ —Б–Ї–Њ–Ї—К—В –љ–∞ –і–Њ–ї–љ–Є—П –ї–Є—Б—В —Й–µ —Б—В–∞–љ–µ –љ–µ –≤ —В–Њ—З–Ї–∞ R, –∞ –≤ —В–Њ—З–Ї–∞ –Ґ.
- –Ф–Є–≤–µ—А–≥–µ–љ—Ж–Є—П. –Ф–≤–µ —Б–Є—Б—В–µ–Љ–Є, –Љ–∞–ї–Ї–Њ —А–∞–Ј–ї–Є—З–∞–≤–∞—Й–Є —Б–µ –њ–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ –≤ –љ–∞—З–∞–ї–Њ—В–Њ, –њ—А–Є –µ–і–љ–∞–Ї—К–≤ —Е–∞—А–∞–Ї—В–µ—А –љ–∞ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –Љ–Њ–≥–∞—В –і–∞ —Б–µ –Њ–Ї–∞–ґ–∞—В –≤ —А–µ–Ј—Г–ї—В–∞—В –љ–∞ –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ –≤ —Б—К—Б—В–Њ—П–љ–Є—П, –Љ–љ–Њ–≥–Њ —Б–Є–ї–љ–Њ —А–∞–Ј–ї–Є—З–љ–Є –њ–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ.
 
–Ь–∞—А—И—А—Г—В–Є –њ–Њ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—З–љ–∞—В–∞ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В
–Ь–∞—А—И—А—Г—В—К—В –њ–Њ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞ –љ–∞ —Б—К—Б—В–Њ—П–љ–Є–µ –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ –Љ–Њ–ґ–µ –і–∞ –Љ–Є–љ–µ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—З–љ–Є—П—В –њ—А–∞–≥ (–Њ—В P –і–Њ R) –Є–ї–Є –љ–µ (–Њ—В –Р –і–Њ B). –°–Є—Б—В–µ–Љ–∞—В–∞ –Љ–Њ–ґ–µ –і–∞ –љ–∞—Б—В—К–њ–Є —В–Њ—З–Ї–∞—В–∞ –љ–∞ –њ—А–µ—Б–Є—З–∞–љ–µ. (—В–Њ—З–Ї–∞—В–∞ –љ–∞ –±–Є—Д—Г—А–Ї–∞—Ж–Є—П), —Б–ї–µ–і –Ї–Њ–µ—В–Њ –і–∞ —Б–ї–µ–і–≤–∞ –≤—Б—П–Ї–∞ –Ї—А–Є–≤–∞ –љ–∞ –±–Є—Д—Г—А–Ї–∞—Ж–Є—П, —В.–µ. –і–∞ —Б–µ –і—К—А–ґ–Є –љ–µ–њ—А–µ–і—Б–Ї–∞–Ј—Г–µ–Љ–Њ. –Ф–≤–µ—В–µ —В–Њ—З–Ї–Є C –Є D, –Ї–Њ–Є—В–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –Љ–љ–Њ–≥–Њ –±–ї–Є–Ј–Ї–Є, –љ–Њ –њ–Њ—Б–ї–µ –Њ—В —В—П—Е —Б–Є—Б—В–µ–Љ–∞—В–∞ –і–∞ —Б–µ –Њ—В–Ї–ї–Њ–љ–Є –і—А–∞–Љ–∞—В–Є—З–љ–Њ –≤ —Б–≤–Њ–µ—В–Њ —А–∞–Ј–≤–Є—В–Є–µ (–Њ—В C –Ї—К–Љ P –Є –Њ—В D –Ї—К–Љ R). –°—К—Й–µ—Б—В–≤—Г–≤–∞—В –≤–µ—А–Њ—П—В–љ–Њ –Є –і—А—Г–≥–Є –Љ–∞—А—И—А—Г—В–Є, –љ—П–Ї–Њ–Є –Њ—В –≤–Ї–ї—О—З–≤–∞—Й–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—З–љ–Њ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞, –і—А—Г–≥–Є - –љ–µ. –°—К–і—К—А–ґ–∞—В–µ–ї–µ–љ —Б–Љ–Є—Б—К–ї —В–µ–Ј–Є –њ–∞—А–∞–Љ–µ—В—А–Є –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ –њ—А–Є–і–Њ–±–Є–≤–∞ –њ—А–Є –Њ–њ–Є—Б–∞–љ–Є–µ —З—А–µ–Ј —В–Њ–Ј–Є –Љ–Њ–і–µ–ї –Ї–∞—В–∞—Б—В—А–Њ—Д–∞ –љ–∞ —Б—К–Њ—В–≤–µ—В–µ–љ –Ї–Њ–љ–Ї—А–µ—В–µ–љ –њ—А–Њ—Ж–µ—Б.
- –њ—А–Є —П—Б–љ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є –љ–∞—З–∞–ї–љ–Є –њ–Њ–Ј–Є—Ж–Є–Є
|
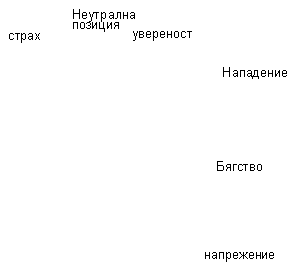 |
| –Э–∞–є-–Є–љ—В–µ—А–µ—Б–љ–Є—В–µ —Б—К–±–Є—В–Є—П —Б—В–∞–≤–∞—В –Ї–Њ–≥–∞—В–Њ –Њ–±–µ–Ї—В—К—В –љ–µ –Ј–∞–µ–Љ–∞ –љ—П–Ї–∞–Ї–≤–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П - –љ–µ –Є–Ј–њ–Є—В–≤–∞ –љ–Є—В–Њ —Г–≤–µ—А–µ–љ–Њ—Б—В, –љ–Є—В–Њ —Б—В—А–∞—Е. –Я—А–Є –љ–∞–≥–љ–µ—В—П–≤–∞–љ–µ –љ–∞ –љ–∞–њ—А–µ–ґ–µ–љ–Є–µ—В–Њ –Њ—В–љ–∞—З–∞–ї–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ—В–Њ –Њ—Б—В–∞–≤–∞ –Є–Ј–≤–µ—Б—В–љ–Њ –≤—А–µ–Љ–µ —Г—А–∞–≤–љ–Њ–≤–µ—Б–µ–љ–Њ - –љ–Є—В–Њ –љ–∞–њ–∞–і–µ–љ–Є–µ, –љ–Є—В–Њ –±—П–≥—Б—В–≤–Њ. –Ю–±–∞—З–µ –њ—А–Є –і–Њ—Б—В–Є–≥–∞–љ–µ –љ–∞ –љ—П–Ї–∞–Ї—К–≤ –Ї—А–Є—В–Є—З–µ–љ –Љ–Њ–Љ–µ–љ—В, —Б—К–≤—Б–µ–Љ –љ–µ–Ј–љ–∞—З–Є—В–µ–ї–љ–Њ —Б—К–±–Є—В–Є–µ –Љ–Њ–ґ–µ –і–∞ –≥–Њ —В–ї–∞—Б–љ–µ –Є–ї–Є –≤ –µ–і–љ–∞—В–∞ –Є–ї–Є –≤ –і—А—Г–≥–∞—В–∞ –Ї—А–∞–є–љ–Њ—Б—В. |
 
-–њ—А–Є –љ–∞—З–∞–ї–љ–∞ –љ–µ—Г—В—А–∞–ї–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П
|
 |
–Я–Њ–і–Њ–±–љ–Њ –љ–∞ —Б—В—К–ї–±, –Ї–Њ–є—В–Њ –њ—А–Є –Ї—А–Є—В–Є—З–љ–Њ –љ–∞—В–Њ–≤–∞—А–≤–∞–љ–µ –Є–Ј–≤–µ–і–љ—К–ґ —Б–µ –Є–Ј–Ї—К–ї—З–≤–∞ - –њ—А–Є –і–Њ—Б—В–∞ –Љ–∞–ї–Ї–Є, –љ–Њ —Б–≤–Њ–µ–≤—А–µ–Љ–µ–љ–љ–Є (–Љ–Њ–ґ–µ –±–Є –і–∞–ґ–µ –љ–µ–Њ—Б—К–Ј–љ–∞—В–Є —Г—Б–Є–ї–Є—П), ¬†—В–Њ–Ј–Є, –Ї–Њ–є—В–Њ –њ—К—А–≤–Є –њ–Њ—З—Г–≤—Б—В–≤–∞ –Љ–Њ–Љ–µ–љ—В–∞ (–Є–ї–Є, –љ–∞ –Ї–Њ–є—В–Њ –њ—А–Њ—Б—В–Њ –Љ—Г –њ—А–Њ–≤—К—А–≤–Є), —Й–µ –і–Њ—Б—В–Є–≥–љ–µ —Г—Б–њ–µ—Е –Є —Й–µ –Љ–Њ–ґ–µ –±—К—А–Ј–Њ –і–∞ –Є–Ј–Љ–µ—Б—В–Є –Ї–Њ–љ–Ї—Г—А–µ–љ—В–∞ —Б–Є –Њ—В –њ–∞–Ј–∞—А–∞. –Ґ–µ–ґ–Ї–Њ –љ–∞ –њ—А–µ–і–њ—А–Є–µ–Љ–∞—З–∞, –Ї–Њ–є—В–Њ –љ–µ —Б—К—Г–Љ–µ–µ –љ–∞–≤—А–µ–Љ–µ –і–∞ —А–∞–Ј–њ–Њ–Ј–љ–∞–µ –љ–∞–Ј—А—П–ї–∞—В–∞ –Њ–њ–∞—Б–љ–Њ—Б—В! –Ч–∞ –љ–µ–≥–Њ —Б—К–±–Є—В–Є—П—В–∞ —Й–µ –њ—А–Є–µ–Љ–∞—В —Д–Њ—А–Љ–∞ –љ–∞ –≤–љ–µ–Ј–∞–њ–љ–Њ –≤—А—К—Е–ї–Є—В–∞—Й–∞ –ї–∞–≤–Є–љ–∞ - –Є–Ј–≤–µ–і–љ—К–ґ, –Ј–∞—А–∞–і–Є –љ—П–Ї–∞–Ї–≤–∞ –і—А–µ–±–Њ–ї–Є—П, –Ј–∞ –Љ–Є–≥ —Й–µ —Б–µ –Њ–Ї–∞–ґ–µ –Ј–∞–і –±–Њ—А–і–∞ –љ–∞ –і–µ–ї–Њ–≤–Є—П –ґ–Є–≤–Њ—В –Ф—А—Г–≥–Є—П—В, "–Ї—К—Б–Љ–µ—В–ї–Є—П—В–∞", –љ–µ–Њ—З–∞–Ї–≤–∞–љ–Њ –Ј–∞ —Б–µ–±–µ —Б–Є, –≤—К–њ—А–µ–Ї–Є —З–µ –µ —А–∞–±–Њ—В–Є–ї —В–∞–Ї–∞, –Ї–∞–Ї—В–Њ –≤–Є–љ–∞–≥–Є, –Є –Є–Ј–≤–µ–і–љ—К–ґ –Ї–∞—В–Њ –Њ—В –љ–µ–±–µ—В–Њ - –љ–µ—З—Г–≤–∞–љ —Г—Б–њ–µ—Е! –Ь–∞–ї–Ї–Њ –Є–Ј–Љ–µ–љ–Є–ї –Њ–њ–∞–Ї–Њ–≤–Ї–∞—В–∞ –Є–ї–Є –і–∞–ї –љ–Њ–≤–∞ —А–µ–Ї–ї–∞–Љ–∞ - –Є —В–∞–Ї—К–≤ –љ–µ–Њ—З–∞–Ї–≤–∞–љ –Њ–≥—А–Њ–Љ–µ–љ –µ—Д–µ–Ї—В.
–Ъ–Њ–ї–Ї–Њ –±–Є—В–Ї–Є —Б–∞ –±–Є–ї–Є —А–µ—И–∞–≤–∞–љ–Є –Њ—В "—А–µ—И–Є—В–µ–ї–љ–∞—В–∞ –љ–∞–Љ–µ—Б–∞" –љ–∞ –љ—П–Ї–∞–Ї—К–≤ –Љ–∞–ї—К–Ї –Њ—В—А—П–і, –і–Њ—И—К–ї –Њ–±–∞—З–µ –љ–∞–≤—А–µ–Љ–µ! –Х—Б—В–µ—Б—В–≤–µ–љ–Њ, –µ–і–љ–∞ –ґ–µ–љ–∞ –љ–µ –Љ–Њ–ґ–µ —Б–њ–Њ–Ї–Њ–є–љ–Њ –і–∞ –≤—К–Ј–њ—А–Є–µ–Љ–µ –і—К–ї–≥–Њ —А–∞–≤–љ–Њ–і—Г—И–љ–Њ—В–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ –Њ—В —Б—В—А–∞–љ–∞ –љ–∞ –Љ—К–ґ–∞, —В–Њ–≤–∞ –Ј–∞—Б—П–≥–∞ –љ–µ–є–љ–Њ—В–Њ –і–Њ—Б—В–Њ–є–љ—Б—В–≤–Њ, –ї–Є—И–∞–≤–∞ —П –Њ—В –і—Г—И–µ–≤–љ–Њ —А–∞–≤–љ–Њ–≤–µ—Б–Є–µ –Є –Љ–Њ–ґ–µ –і–∞ —П –і–Њ–≤–µ–і–µ –і–Њ —В–Њ—З–Ї–∞—В–∞, –Ї–Њ–≥–∞—В–Њ –љ–µ—Г—В—А–∞–ї–љ–Њ—В–Њ –є –і–Њ—Б–µ–≥–∞ –Њ—В–љ–Њ—И–µ–љ–Є–µ –Ї—К–Љ –њ–∞—А—В–љ—М–Њ—А–∞ —Б—В–∞–≤–∞ –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ. –Ч–∞ –Љ—К–ґ–∞ –µ –Љ–љ–Њ–≥–Њ –≤–∞–ґ–љ–Њ –і–∞ —Е–≤–∞–љ–µ —В–Њ–Ј–Є –Љ–Њ–Љ–µ–љ—В –Є –і–∞–ґ–µ —Б—К–≤—Б–µ–Љ –Љ–∞–ї–Ї–∞ –њ—А–Њ—П–≤–∞ –љ–∞ –≤–љ–Є–Љ–∞–љ–Є–µ –Љ–Њ–ґ–µ –і–∞ —П –љ–∞–Ї–∞—А–∞ —Б—В—А–∞—Б—В–љ–Њ –і–∞ —Б–µ –≤–ї—О–±–Є, –≤ —Б—К—Й–Њ—В–Њ –≤—А–µ–Љ–µ - —Б—К–≤—Б–µ–Љ –Љ–∞–ї–Ї–Є –њ—А–Є—З–Є–љ–Є –Љ–Њ–≥–∞—В –і–∞ —П –љ–∞–њ—А–∞–≤—П—В –≤–∞—И –≤—А–∞–≥. –Р –ґ–µ–љ–Є—В–µ? –Ґ–µ, –љ–∞ —Б–≤–Њ–є —А–µ–і, –Њ–±–Є—З–∞—В –і–∞ –≤–Њ–і—П—В —Б–≤–Њ–Є—В–µ –њ–∞—А—В–љ—М–Њ—А–Є –њ–Њ –љ–∞–њ—А–µ—З–љ–Є—В–µ –Љ–∞—А—И—А—Г—В–Є –њ–Њ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—З–љ–∞—В–∞ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В. –°–њ–Њ–Љ–љ–µ—В–µ —Б–Є "–Ъ–∞—А–Љ–µ–љ" - –ґ–µ–љ–∞—В–∞ —В—Г –њ—А–Є–±–ї–Є–ґ–∞–≤–∞ –Ї—К–Љ –Љ—К–ґ–∞, —В—Г –љ–∞–і—Б–Љ–Є–≤–∞–є–Ї–Є –Љ—Г —Б–µ –≥–Њ –њ—А–Њ–≥–Њ–љ–≤–∞, –Є –Њ—В–љ–Њ–≤–Њ - —Б—К—Й–Є—П —Ж–Є–Ї—К–ї. –•–≤—К—А–ї—П –љ–µ—Й–∞—Б—В–љ–Є–Ї–∞ –Њ—В —Б—К—Б—В–Њ—П–љ–Є–µ –љ–∞ –њ–ї–∞–Љ–µ–љ–љ–∞ –ї—О–±–Њ–≤ –≤ –Њ—В—З–∞—П–љ–∞ –љ–µ–љ–∞–≤–Є—Б—В –Є –Њ–±—А–∞—В–љ–Њ. –Ш —В–∞–Ї–∞, –і–Њ–Ї–∞—В–Њ –љ–µ –≥–Њ –і–Њ–Ї–∞—А–∞ –і–Њ –Є–Ј—Б—В—К–њ–ї–µ–љ–Є–µ (–Є –њ—А–µ—Б—В—К–њ–ї–µ–љ–Є–µ).
-–њ—А–Є –љ–∞–њ—А–µ—З–µ–љ –Љ–∞—А—И—А—Г—В
|
 |
–Ь–љ–Њ–≥–Њ –≤–∞–ґ–µ–љ –Љ–Њ–Љ–µ–љ—В –µ —Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В—В–∞ –љ–∞ –љ–∞—И–Є—В–µ –њ—А–µ–і—Б—В–∞–≤–Є. –Р–Ї–Њ —З–Њ–≤–µ–Ї –µ –≤–µ—З–µ –Ј–∞–µ–ї –∞–Ї—В–Є–≤–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П, —В–Њ –љ–µ —Й–µ –±—К–і–µ –Є–Ј–≤–µ–і–µ–љ –Њ—В –љ–µ—П, –і–∞–ґ–µ –њ—А–Є –≤—К–Ј–љ–Є–Ї–љ–∞–ї –ї–µ–Ї —Б—В—А–∞—Е –њ—А–µ–і –і–µ–є—Б—В–≤–Є—В–µ–ї–љ–∞—В–∞ —Б–ї–Њ–ґ–љ–Њ—Б—В –љ–∞ –њ—А–Њ–±–ї–µ–Љ–∞. –Ю–±–∞—З–µ, –∞–Ї–Њ —Г–≤–µ—А–µ–љ–Њ—Б—В—В–∞ –Љ—Г –≤ —Б–≤–Њ–Є—В–µ —Б–Є–ї–Є –љ–∞–Љ–∞–ї–µ–µ –і–Њ –Њ–њ–∞—Б–µ–љ –њ—А–µ–і–µ–ї, —В–Њ–є —А—П–Ј–Ї–Њ —Й–µ —Б–Љ–µ–љ–Є –Љ–Њ–і–µ–ї–∞ —Б–Є –љ–∞ –њ–Њ–≤–µ–і–µ–љ–Є—П: –љ–∞–њ–∞–і–∞—Й–Є—П —Б–µ –Њ–±—А—К—Й–∞ –≤ –±—П–≥—Б—В–≤–Њ, –∞—В–∞–Ї—Г–≤–∞—Й–Є—П—В —Й–µ –Ј–∞–µ–Љ–µ –Њ—В–±—А–∞–љ–Є—В–µ–ї–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П. –°–µ–≥–∞ - –Њ–±—А–∞—В–љ–Њ, –і–∞–ґ–µ –њ–Њ—П–≤–Є–ї–∞ —Б–µ —Г–≤–µ—А–µ–љ–Њ—Б—В –≤ —Б–≤–Њ–Є—В–µ —Б–Є–ї–Є –љ–µ –њ–Њ–Ј–≤–Њ–ї—П–≤–∞ –љ–∞ —З–Њ–≤–µ–Ї–∞ –і–∞ –Є–Ј–ї–µ–Ј–µ –Њ—В –њ–∞—Б–Є–≤–љ–Њ—В–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ. –Ч–∞—В–Њ–≤–∞ –µ —В–Њ–ї–Ї–Њ–≤–∞ —В—А—Г–і–љ–Њ –і–∞ —Б–µ –Њ–±—К—А–љ–µ —А–µ–Ј—Г–ї—В–∞—В–∞, –Ї–Њ–≥–∞—В–Њ —Д—Г—В–±–Њ–ї–љ–Є—П—В –Њ—В–±–Њ—А –≥—Г–±–Є. –°–∞–Љ–Њ –Ј–љ–∞—З–Є—В–µ–ї–љ–Є –њ—А–Є–ї–Є–≤–Є –љ–∞ —А–µ—И–Є—В–µ–ї–љ–Њ—Б—В –Љ–Њ–≥–∞—В –і–∞ –і–Њ–≤–µ–і–∞—В –і–Њ —В–Њ–≤–∞, —З–µ –Њ—В–±—А–∞–љ—П–≤–∞—Й–Є—П —Б–µ –і–∞ —Б–µ —Е–≤—К—А–ї–Є –љ–∞–њ—А–µ–і.
–£–њ—А–∞–≤–ї–µ–љ–Є–µ –љ–∞ —А–Є—Б–Ї–∞
–£–њ—А–∞–≤–ї–µ–љ–Є–µ—В–Њ –љ–∞ —А–Є—Б–Ї–∞ –µ –µ–і–љ–∞ –Њ—В –љ–∞–є-–≤–∞–ґ–љ–Є—В–µ —В–µ—Е–љ–Њ–ї–Њ–≥–Є–Є –љ–∞ –љ–∞—И–∞—В–∞ —Ж–Є–≤–Є–ї–Є–Ј–∞—Ж–Є—П. –Т—К–Њ–±—Й–µ, —В–Њ–≤–∞ –µ –Љ–∞–≥–Є—Б—В—А–∞–ї–љ–Є—П –њ—К—В –љ–∞ –њ—А–Њ–≥—А–µ—Б–∞: –і–∞ –Ј–∞–Љ–µ–љ—П–Љ–µ –µ–і–љ–Є –Ј–∞–њ–ї–∞—Е–Є –Є –Њ–њ–∞—Б–љ–Њ—Б—В–Є —Б –і—А—Г–≥–Є. –Э–∞–њ—А–Є–Љ–µ—А, –Њ–њ–∞—Б–љ–Њ—Б—В—В–∞ –і–∞ –≥–ї–∞–і—Г–≤–∞–Љ–µ –Є –Є–Ј–Љ—А—К–Ј–≤–∞–Љ–µ —Б —А–Є—Б–Ї–∞ –і–∞ –њ–Њ–ґ—К–љ–µ–Љ –њ–ї–Њ–і–Њ–≤–µ—В–µ –Њ—В –Ј–∞—А–∞–Ј—П–≤–∞–љ–µ—В–Њ –љ–∞ –≤–Њ–і–Є—В–µ, –Ј–µ–Љ—П—В–∞, –≤—К–Ј–і—Г—Е–∞, —Б–≤—К—А–Ј–∞–љ–Њ —Б —В—А–∞–і–Є—Ж–Є–Њ–љ–љ–Є—В–µ –љ–Є –љ–∞—З–Є–љ–Є –Ј–∞ –і–Њ–±–Є–≤–∞–љ–µ –љ–∞ –µ–љ–µ—А–≥–Є—П.
–Т—К–Ј–Љ–Њ–ґ–љ–Њ—Б—В—В–∞ –і–∞ –Ј–љ–∞–µ–Љ –Є –≤–Є–і–Є–Љ —Б—В–∞–≤–∞—Й–Њ—В–Њ –љ–∞ —Е–Є–ї—П–і–Є –Ї–Є–ї–Њ–Љ–µ—В—А–Є, —Б–µ –Њ–Ї–∞–Ј–≤–∞ —Б–≤—К—А–Ј–∞–љ–∞ —Б –ґ–Є–≤–Њ—В —Б—А–µ–і –Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Њ–љ–µ–љ —И—Г–Љ, —Б—А–µ–і —А–µ–Ї–ї–∞–Љ–љ–Њ-–Є–љ—Д–Њ—А–Љ–∞—Ж–Є–Њ–љ–љ–Њ –±—Г–љ–Є—Й–µ –Є –Њ–Ї–µ–∞–љ –Њ—В –ї—К–ґ–Є. –Э–µ —В—А—П–±–≤–∞ –і–∞ –Љ–Є—Б–ї–Є–Љ, —З–µ "–љ—П–Љ–∞ –∞–ї—В–µ—А–љ–∞—В–Є–≤–∞", –Ї–∞–Ї—В–Њ –љ–Є –Ї–∞–Ј–≤–∞—В –љ–∞—И–Є—В–µ –њ–Њ–ї–Є—В–Є—Ж–Є. –Ш–Љ–∞ –∞–ї—В–µ—А–љ–∞—В–Є–≤–∞. –Ф—К–ї–±–Њ–Ї–∞—В–∞ –≤—А—К–Ј–Ї–∞ –Љ–µ–ґ–і—Г –Є–і–µ–Є—В–µ –љ–∞ –љ–µ–ї–Є–љ–µ–є–љ–∞—В–∞ –і–Є–љ–∞–Љ–Є–Ї–∞ –Є —Г–њ—А–∞–≤–ї–µ–љ–Є–µ—В–Њ –љ–∞ —А–Є—Б–Ї–∞ —Б—В–∞–љ–∞–ї–∞ —П—Б–љ–∞ —Б—А–∞–≤–љ–Є—В–µ–ї–љ–Њ –љ–µ–Њ—В–і–∞–≤–љ–Њ.
–Ч–∞ –і–∞ —Б–µ –Њ—Б—К–Ј–љ–∞–µ –њ–Њ–Љ–Њ–≥–љ–∞–ї–∞ –њ–∞—А–∞–і–Њ–Ї—Б–∞–ї–љ–∞—В–∞ —Б—В–∞—В–Є—Б—В–Є–Ї–∞ –љ–∞ –∞–≤–∞—А–Є–Є—В–µ¬†–і–∞ —Б–Є —Б–њ–Њ–Љ–љ–Є–Љ "–Ґ–Є—В–∞–љ–Є–Ї", "–І–µ–ї–µ–љ–і–ґ—К—А", –І–µ—А–љ–Њ–±–Є–ї, –Ґ—А–Є–Љ–∞–є–ї, –С—Е–Њ–њ–∞–ї... –Т—Б—П–Ї–∞ –Њ—В —В–µ–Ј–Є –љ–∞–є-–Ї—А—Г–њ–љ–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є –љ–∞ XX –≤–µ–Ї —Б–∞ —Б–≤—К—А–Ј–∞–љ–Є —Б –і—К–ї–≥–∞ –≤–µ—А–Є–≥–∞ –Њ—В —Б–ї—Г—З–∞–є–љ–Є –њ—А–Є—З–Є–љ–љ–Њ—Б–ї–µ–і—Б—В–≤–µ–љ–Є –≤—А—К–Ј–Ї–Є. –Р –≤ –љ–∞—Б –Њ—Б—В–∞–≤–∞ —З—Г–≤—Б—В–≤–Њ—В–Њ, —З–µ –њ—А–Њ—Б—В–Њ –љ–µ –љ–Є –≤—К—А–≤–Є.
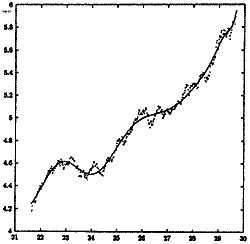
–Ю–±—К—А–љ–µ—В–µ –≤–љ–Є–Љ–∞–љ–Є–µ –љ–∞ –і–≤–µ—В–µ –і–Є–∞–≥—А–∞–Љ–Є¬†–≥–Њ—А–µ. –Т–ї—П–≤–Њ –њ–Њ –Њ—А–і–Є–љ–∞—В–∞—В–∞ –µ –Њ—В–ї–Њ–ґ–µ–љ –ї–Њ–≥–∞—А–Є—В—К–Љ–∞ –љ–∞ –Є–Ј–Љ–µ–љ–µ–љ–Є–µ—В–Њ –љ–∞ –Є–љ–і–µ–Ї—Б–∞ –Ф–Њ—Г-–Ф–ґ–Њ–љ—Б, –њ–Њ –∞–±—Б—Ж–Є—Б–∞—В–∞ –µ –≤—А–µ–Љ–µ—В–Њ. –Я–Њ–Ї–∞–Ј–∞–љ –µ –њ–µ—А–Є–Њ–і–∞ –њ—А–µ–і –Т–µ–ї–Є–Ї–∞—В–∞ –і–µ–њ—А–µ—Б–Є—П –Њ—В 1929 –≥. –Ш–љ–і–µ–Ї—Б –Ф–Њ—Г-–Ф–ґ–Њ–љ—Б –µ –µ–і–Є–љ –Њ—В –≥–ї–∞–≤–љ–Є—В–µ –Є–љ–і–Є–Ї–∞—В–Њ—А–Є –љ–∞ —Б—К—Б—В–Њ—П–љ–Є—П –љ–∞ –Є–Ї–Њ–љ–Њ–Љ–Є–Ї–∞—В–∞ - —Е–∞—А–∞–Ї—В–µ—А–Є–Ј–Є—А–∞ —Б—А–µ–і–љ–∞—В–∞ –њ–∞–Ј–∞—А–љ–∞ —Б—В–Њ–є–љ–Њ—Б—В –љ–∞ –µ–і–љ–∞ –∞–Ї—Ж–Є—П.
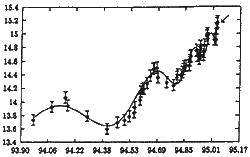
–Т–і—П—Б–љ–Њ –µ –≥—А–∞—Д–Є–Ї–∞ –љ–∞ –Ї–Њ–љ—Ж–µ–љ—В—А–∞—Ж–Є—П—В–∞ –љ–∞ —Е–ї–Њ—А–љ–Є—В–µ –є–Њ–љ–Є –≤ –Є–Ј–≤–Њ—А–Є—В–µ –≤ –љ–∞–≤–µ—З–µ—А–Є–µ—В–Њ –љ–∞ –Ј–µ–Љ–µ—В—А–µ—Б–µ–љ–Є–µ—В–Њ –≤ –Ъ–Њ–±–µ 1995 –≥. –Ф–≤–µ—В–µ –Ї—А–Є–≤–Є —Б–∞ –Љ–љ–Њ–≥–Њ —Б—Е–Њ–і–љ–Є –Є –і–≤–µ—В–µ —Б–µ –Њ–њ–Є—Б–≤–∞—В —Б –≤–Є—Б–Њ–Ї–∞ —В–Њ—З–љ–Њ—Б—В –Њ—В –µ–і–љ–∞ —Д–Њ—А–Љ—Г–ї–∞. –Ш —П–≤–љ–Њ –Ј–∞–і —В–Њ–≤–∞ —Б—Е–Њ–і—Б—В–≤–Њ —Б–µ –Ї—А–Є–µ –∞–љ–∞–ї–Њ–≥–Є—П –Љ–µ–ґ–і—Г –Љ–µ—Е–∞–љ–Є–Ј–Љ–Є—В–µ –Є –љ–∞ –і–≤–µ—В–µ —П–≤–ї–µ–љ–Є—П –Є –≤—К–Ј–Љ–Њ–ґ–љ–Њ—Б—В –і–∞ —Б–µ –њ—А–µ–љ–µ—Б–∞—В –Љ–µ—В–Њ–і–Є—В–µ –Ј–∞ –њ—А–Њ–≥–љ–Њ–Ј–∞ –Њ—В –µ–і–љ–∞ –Њ–±–ї–∞—Б—В –≤ –і—А—Г–≥–∞. –Ґ–Њ–≤–∞, —З–µ –љ–∞–є-—А–∞–Ј–ї–Є—З–љ–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—З–љ–Є —Б—К–±–Є—В–Є—П –Љ–Њ–≥–∞—В –і–∞ —Б–µ —А–∞–Ј–≤–Є–≤–∞—В –њ–Њ –µ–і–љ–Є –Є —Б—К—Й–Є –Ј–∞–Ї–Њ–љ–Є, –µ –љ–∞–і–µ–ґ–і–∞ –Ј–∞ —В—П—Е–љ–Њ—В–Њ —А–∞–Ј–≥–∞–і–∞–≤–∞–љ–µ.
–°–њ—А–∞–≤–Ї–∞: –°—А–∞–≤–љ–Є—В–µ–ї–љ–∞ —В–∞–±–ї–Є—Ж–∞ –љ–∞ –≤–Є–і–Њ–≤–µ—В–µ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є
| –Ъ–∞—В–∞—Б—В—А–Њ—Д–Є / —Г—А–∞–≤–љ–µ–љ–Є–µ | –С—А–Њ–є –Њ—Б–Є –љ–∞ –њ–Њ–≤–µ–і–µ–љ–Є–µ | –С—А–Њ–є –њ–∞—А–∞–Љ–µ—В—А–Є (–£–њ—А–∞–≤–ї—П–≤–∞—Й–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ) | –С–µ–ї–µ–ґ–Ї–Є |
|
–У—К–љ–Ї–∞ (fold) x3 + ax |
1 | 1 (–µ–і–љ–Њ–Љ–µ—А–љ–Њ) | –С–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ–∞ –≥—А—Г–њ–∞ –Њ—В –µ–і–љ–∞ —В–Њ—З–Ї–∞. –Ґ–Њ–Ј–Є –Љ–Њ–і–µ–ї –µ –∞–љ–∞–ї–Њ–≥–Є—З–µ–љ –љ–∞ –Ј–∞–Ї–Њ–љ–∞ "–≤—Б–Є—З–Ї–Њ –Є–ї–Є –љ–Є—Й–Њ".–Э—П–Љ–∞ —В–Њ—З–Ї–∞ –љ–∞ –њ—А–µ—Б–Є—З–∞–љ–µ. |
|
–Т–Є—В–ї–Њ (cusp) x4 + ax2 + bx |
1 | 2 (–і–≤—Г–Љ–µ—А–љ–Њ) | –С–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ–∞ –≥—А—Г–њ–∞ –Њ—В –і–≤–µ—В–µ –ї–Є–љ–Є–Є –љ–∞ —Б–≥—К–≤–∞–љ–µ –Є –µ–і–љ–∞ –Њ—Б—В—А–Њ–≤—К—А—Е–∞ —В–Њ—З–Ї–∞ –љ–∞ —Б–ї–Є–≤–∞–љ–µ –љ–∞ –і–≤–µ—В–µ –ї–Є–љ–Є–Є. |
|
–Ы—П—Б—В–Њ–≤–Є—З–∞ –Њ–њ–∞—И–Ї–∞ (swallowtail) x5 + ax3 + bx2 + cx |
1 | 3 (—В—А–Є–Љ–µ—А–љ–Њ) | –С–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ–∞ –≥—А—Г–њ–∞ –Њ—В —В—А–Є –њ–Њ–≤—К—А—Е–љ–Њ—Б—В–Є –љ–∞ —В–Њ—З–Ї–Є—В–µ –љ–∞ —Б–≥—К–≤–∞–љ–µ (–ї–Є–љ–Є–Є—В–µ –љ–∞ –Є–Ј—А—П–Ј–≤–∞–љ–µ –≤ —Г–њ—А–∞–≤–ї—П–≤–∞—Й–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ), –Ї–Њ–Є—В–Њ —Б–µ —Б—А–µ—Й–∞—В –≤ –і–≤–µ –ї–Є–љ–Є–Є —В–Њ—З–Ї–Є –љ–∞ –њ—А–µ—Б–Є—З–∞–љ–µ, –Ї–Њ–Є—В–Њ —Б–µ —Б–∞–Љ–Њ–Ј–∞—Б–Є—З–∞—В –≤ –ї—П—Б—В–Њ–≤–Є—З–∞ –Њ–њ–∞—И–Ї–∞. |
–•–Є–њ–µ—А–±–Њ–ї–Є—З–љ–∞ –Њ–Љ–±–Є–ї–Є–Ї–∞x3 + y3 + axy + bx + cy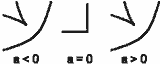 |
2 | 3 (—В—А–Є–Љ–µ—А–љ–Њ) | –Э—Г–ї–µ–≤–∞—В–∞ —В–Њ—З–Ї–∞ –љ–∞ —Е–Є–њ–µ—А–±–Њ–ї–Є—З–љ–∞—В–∞ –≥—А—Г–њ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є –Љ–Њ–ґ–µ –і–∞ —Б–µ —А–∞–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –Ї–Њ–ї–∞–њ—Б –љ–∞ –µ–і–Є–љ –Љ–Є–љ–Є–Љ—Г–Љ, –µ–і–Є–љ –Љ–∞–Ї—Б–Є–Љ—Г–Љ –Є –і–≤–µ —Б–µ–і–ї–∞. |
|
–Х–ї–Є–њ—В–Є—З–љ–∞ –Њ–Љ–±–Є–ї–Є–Ї–∞ x3/3 - xy2 + a(x2 + y2) + bx + cy
|
2 | 3 (—В—А–Є–Љ–µ—А–љ–Њ) | –Э—Г–ї–µ–≤–∞—В–∞ —В–Њ—З–Ї–∞ –љ–∞ –µ–ї–Є–њ—В–Є—З–љ–∞—В–∞ –≥—А—Г–њ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є –Љ–Њ–ґ–µ –і–∞ —Б–µ —А–∞–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –Ї–Њ–ї–∞–њ—Б –љ–∞ –µ–і–Є–љ –Љ–Є–љ–Є–Љ—Г–Љ–∞ –Є–ї–Є –µ–і–Є–љ –Љ–∞–Ї—Б–Є–Љ—Г–Љ –Є —В—А–Є —Б–µ–і–ї–∞. –њ—А–Є c<- 1 –Є–Љ–∞–Љ–µ –і–≤–∞ —Б–µ–і–ї–∞, –Ї–Њ–Є—В–Њ —Б —Г–≤–µ–ї–Є—З–∞–≤–∞–љ–µ—В–Њ –љ–∞ c —Б–µ –і–≤–Є–ґ–∞—В –њ–Њ –ї–Є–љ–Є—П—В–∞ y=- 1 –µ–і–љ–Њ —Б—А–µ—Й—Г –і—А—Г–≥–Њ ; –њ—А–Є c=- 1 –≤ —В–Њ—З–Ї–∞—В–∞ x= 0, y= 1 —Б–µ —А–∞–ґ–і–∞ –Љ–Є–љ–Є–Љ—Г–Љ –Є —Б–µ–і–ї–Њ ; –њ—А–Є -1< c< 3 —В–µ–Ј–Є —Б–µ–і–ї–Њ –Є –Љ–Є–љ–Є–Љ—Г–Љ —Б–µ —А–∞–Ј–і–∞–ї–µ—З–∞–≤–∞—В –њ–Њ –Њ—Б—В–∞ x –≤ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —Б—В—А–∞–љ–Є, –∞ –і–≤–µ—В–µ –Є–Ј—Е–Њ–і–љ–Є —Б–µ–і–ї–∞ –њ—А–Њ–і—К–ї–ґ–∞–≤–∞ –і–∞ —Б–µ —Б–±–ї–Є–ґ–∞–≤–∞—В; –њ—А–Є c= 3 –і–≤–µ—В–µ —Б–µ–і–ї–∞ –Є –Љ–Є–љ–Є–Љ—Г–Љ —Б–µ —Б–ї–Є–≤–∞—В –≤ —В–Њ—З–Ї–∞ x= 0, y=- 1; –њ—А–Є c> 3 –Њ—Б—В–∞–≤–∞—В –і–≤–∞ —Б–µ–і–ї–∞, –Ї–Њ–Є—В–Њ —Б–µ —А–∞–Ј–і–∞–ї–µ—З–∞–≤–∞—В –њ–Њ –Њ—Б—В–∞ x —Б—К—Б —Б—В–Њ–є–љ–Њ—Б—В c. |
|
–Я–µ–њ–µ—А—Г–і–∞ x6 + ax4 + bx3 + cx2 + dx |
1 | 4 | –£–њ—А–∞–≤–ї—П–≤–∞—Й–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –µ —З–µ—В–Є—А–Є–Љ–µ—А–љ–Њ. –Ш–Љ–∞ —В—А–Є —В–Њ—З–Ї–Є –љ–∞ –њ—А–µ—Б–Є—З–∞–љ–µ. –С–Є—Д—Г—А–Ї–∞—Ж–Є–Њ–љ–љ–∞ –≥—А—Г–њ–∞ –Њ—В –њ—А–µ–≥—К–љ–∞—В–Є —Е–Є–њ–µ—А–њ–Њ–≤—К—А—Е–љ–Њ—Б—В–Є (–ї–Є–љ–Є–Є—В–µ –љ–∞ –Є–Ј—А—П–Ј–≤–∞–љ–µ –≤ —Г–њ—А–∞–≤–ї—П–≤–∞—Й–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ), –Ї–Њ–Є—В–Њ —Б–µ —Б—А–µ—Й–∞—В –љ–∞ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В –Њ—В —В–Њ—З–Ї–Є –љ–∞ –њ—А–µ—Б–Є—З–∞–љ–µ, –Ї–Њ–Є—В–Њ —Б–µ —Б–∞–Љ–Њ–Ј–∞—Б–Є—З–∞—В –≤ –ї–Є–љ–Є–Є –љ–∞ –ї—П—Б—В–Њ–≤–Є—З–∞ –Њ–њ–∞—И–Ї–∞. –Э–∞–Ї—А–∞—П —В–µ–Ј–Є –ї–Є–љ–Є–Є –љ–∞ –ї—П—Б—В–Њ–≤–Є—З–∞ –Њ–њ–∞—И–Ї–∞ —Б—А–µ—Й–∞—В –Ј–∞–µ–і–љ–Њ –≤ —В–Њ—З–Ї–∞ –≤—К–≤ –≤–Є–і –љ–∞ –њ–µ–њ–µ—А—Г–і–∞. –Т —В–∞–Ј–Є —В–Њ—З–Ї–∞ –≤ —Г–њ—А–∞–≤–ї—П–≤–∞—Й–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ, –њ–Њ—В–µ–љ—Ж–Є–∞–ї–љ–∞—В–∞ –Ї—А–Є–≤–∞ –Є–Љ–∞ —Б–∞–Љ–Њ –µ–і–Є–љ –Љ–Є–љ–Є–Љ—Г–Љ, –Ї–Њ–є—В–Њ —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞ –љ–∞ —Г–љ–Є—Й–Њ–ґ–∞–≤–∞–љ–µ—В–Њ –љ–∞ —В—А–Є –Љ–Є–љ–Є–Љ—Г–Љ–∞ –Є –і–≤–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞. |
|
–Я–∞—А–∞–±–Њ–ї–Є—З–љ–∞ –Њ–Љ–±–Є–ї–Є–Ї–∞ x2y + y4 + ax2 + by2 + cx + dy |
2 | 4 | –Э—Г–ї–µ–≤–∞—В–∞ —В–Њ—З–Ї–∞ –љ–∞ –њ–∞—А–∞–±–Њ–ї–Є—З–љ–љ–∞—В–∞ –≥—А—Г–њ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є –Љ–Њ–ґ–µ –і–∞ —Б–µ —А–∞–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –Ї–Њ–ї–∞–њ—Б –љ–∞ –і–≤–∞ –Љ–Є–љ–Є–Љ—Г–Љ–∞ –Є–ї–Є –і–≤–∞ –Љ–∞–Ї—Б–Є–Љ—Г–Љ–∞ –Є–ї–Є –µ–і–Є–љ –Љ–∞–Ї—Б–Є–Љ—Г–Љ –Є –µ–і–Є–љ –Љ–Є–љ–Є–Љ—Г–Љ –Є —В—А–Є —Б–µ–і–ї–∞. –Я–∞—А–∞–±–Њ–ї–Є—З–љ–∞ –Њ–Љ–±–Є–ї–Є–Ї–∞ –µ –љ–∞–є-—Б–ї–Њ–ґ–љ–∞—В–∞ —Б—А–µ–і 7-—В–µ –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є. –Ы–Є–љ–Є—П—В–∞ —Б —Г—А–∞–≤–љ–µ–љ–Є–µ - b = -6a2, c = 0, d = -8a3 e –љ–∞—А–µ—З–µ–љ–∞ "–Њ–Љ–±–Є–ї–Є–Ї–∞". |
–Ш–Ј—В–Њ—З–љ–Є—Ж–Є:
–Р–љ–∞—В–Њ–Љ–Є—П –Ї–∞—В–∞–Ї–ї–Є–Ј–Љ–∞, –Р–ї–µ–Ї—Б–∞–љ–і—А –С–ї–Є–љ–Ї–Њ–≤, –Р–љ–і—А–µ–є –Ъ–Є—Б–µ–ї–µ–≤
Elementary catastrophe theory: an introduction
Catastrophe theory, E. C. Zeeman
Catastrophe Theory,  Eric W. Weisstein 
A nonequilibrium thermodynamic framework for discussing ecosystem integrity, James J. Kay
Self-Organization and Leadership Emergence, Nonlin. Dyn., Psych. & Life Sciences
An Introduction to Cusp Surface Analysis, Loren Cobb, PhD.
A STRUCTURE FOR EMBODIED HUMAN CONSCIOUSNESS S. D. Stoney, Dept. of Physiology and Endocrinology, Medical College of Georgia, Augusta, GA 30912-3000
Social processes as dynamical processes: Qualitative dynamical systems theory in social psychology, Watters, PA and Ball, PJ and Carr
Applied catastrophe theory in the social and biological sciences M. A. B. Deakin
The NIB front bifurcation and spontaneous front reversals
–®–µ–ї–µ–њ–Є–љ –Ы. –Р. –Т–і–∞–ї–Є –Њ—В —А–∞–≤–љ–Њ–≤–µ—Б–Є—П
–Ю —В–µ–Њ—А–Є–Є –Ї–∞—В–∞—Б—В—А–Њ—Д (–Ь–∞–љ–µ–≤–Є—З –Ы.–Ш. , 2000)
Contrasting Concepts of Competitive State-Anxiety in Sport: Multidimensional Anxiety and Catastrophe Theories., Ivan M.McNally
Dichotomy or Dialectic [Human Systems Management 4 (1983)] Jamshid Gharajedaghi
The Transition As A Catastrophe: From Theory To Policy, 1994 By Gancho Ganchev
CATASTROPHE TEACHER an introduction for experimentalists
Self Injurious Behaviour - A Model from Catastrophe Theory
Catastrophe theory, Alexei Sharov
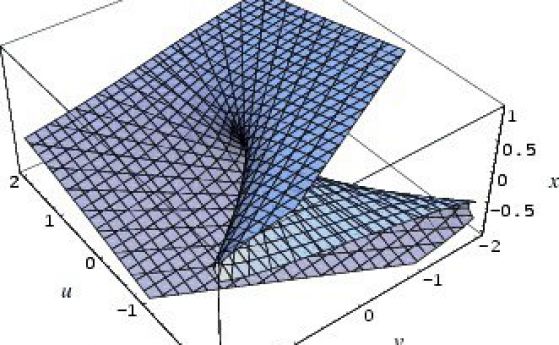

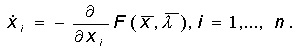 –Т —В–Њ–Ј–Є —Б–ї—Г—З–∞–є, –Ї–Њ–≥–∞—В–Њ –±—А–Њ—П –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –љ–µ –њ—А–µ–≤–Є—И–∞–≤–∞ —З–µ—В–Є—А–Є, —Б–µ –Њ–Ї–∞–Ј–≤–∞, —З–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –і–∞–і–µ –Њ–±—Й–∞ –Ї–ї–∞—Б–Є—Д–Є–Ї–∞—Ж–Є—П –љ–∞ –≤—Б–Є—З–Ї–Є —В–Є–њ–Њ–≤–µ —Б—В—А—Г–Ї—В—Г—А–љ–Є –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є, –љ–∞—А–µ—З–µ–љ–Є –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є. –Ч–љ–∞—З–µ–љ–Є–µ—В–Њ –љ–∞ –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ —Б–µ —Б—К—Б—В–Њ–Є –≤ —В–Њ–≤–∞, —З–µ —В—П —Б–≤–µ–ґ–і–∞ –Њ–≥—А–Њ–Љ–љ–Њ—В–Њ –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ –љ–∞ —Б–Є—В—Г–∞—Ж–Є–Є –і–Њ –Љ–∞–ї—К–Ї –±—А–Њ–є —Б—В–∞–љ–і–∞—А—В–љ–Є —Б—Е–µ–Љ–Є, –Ї–Њ–Є—В–Њ –Љ–Њ–ґ–µ –і–µ—В–∞–є–ї–љ–Њ –і–∞ —Б–µ –Є–Ј—Б–ї–µ–і–≤–∞—В –≤–µ–і–љ—К–ґ –Є –Ј–∞–≤–Є–љ–∞–≥–Є.
–Т —В–Њ–Ј–Є —Б–ї—Г—З–∞–є, –Ї–Њ–≥–∞—В–Њ –±—А–Њ—П –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –љ–µ –њ—А–µ–≤–Є—И–∞–≤–∞ —З–µ—В–Є—А–Є, —Б–µ –Њ–Ї–∞–Ј–≤–∞, —З–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –і–∞–і–µ –Њ–±—Й–∞ –Ї–ї–∞—Б–Є—Д–Є–Ї–∞—Ж–Є—П –љ–∞ –≤—Б–Є—З–Ї–Є —В–Є–њ–Њ–≤–µ —Б—В—А—Г–Ї—В—Г—А–љ–Є –љ–µ—Г—Б—В–Њ–є—З–Є–≤–Њ—Б—В–Є, –љ–∞—А–µ—З–µ–љ–Є –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–Є –Ї–∞—В–∞—Б—В—А–Њ—Д–Є. –Ч–љ–∞—З–µ–љ–Є–µ—В–Њ –љ–∞ –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Ї–∞—В–∞—Б—В—А–Њ—Д–Є—В–µ —Б–µ —Б—К—Б—В–Њ–Є –≤ —В–Њ–≤–∞, —З–µ —В—П —Б–≤–µ–ґ–і–∞ –Њ–≥—А–Њ–Љ–љ–Њ—В–Њ –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ –љ–∞ —Б–Є—В—Г–∞—Ж–Є–Є –і–Њ –Љ–∞–ї—К–Ї –±—А–Њ–є —Б—В–∞–љ–і–∞—А—В–љ–Є —Б—Е–µ–Љ–Є, –Ї–Њ–Є—В–Њ –Љ–Њ–ґ–µ –і–µ—В–∞–є–ї–љ–Њ –і–∞ —Б–µ –Є–Ј—Б–ї–µ–і–≤–∞—В –≤–µ–і–љ—К–ґ –Є –Ј–∞–≤–Є–љ–∞–≥–Є.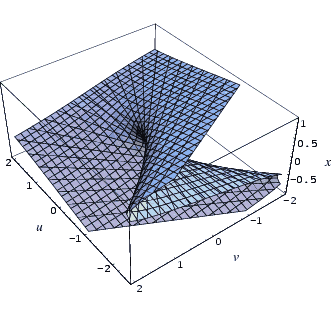
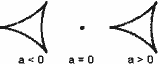


















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
03.08 2015 –≤ 09:52
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
dolivo
–Ч–µ–Љ–љ–∞—В–∞ —П–±—К–ї–Ї–∞: —Б—В–∞—А–∞ –Ї—Г–ї—В—Г—А–∞ –Ј–∞ –љ–Њ–≤–Є—В–µ –Ї–ї–Є–Љ–∞—В–Є—З–љ–Є –≤—А–µ–Љ–µ–љ–∞
dolivo
–Ч–µ–Љ—П—В–∞ –њ–Њ—В—К–Љ–љ—П–≤–∞. –Ъ–∞–Ї–≤–Њ –Њ–Ј–љ–∞—З–∞–≤–∞ —В–∞–Ј–Є —В—А–µ–≤–Њ–ґ–љ–∞ –Ї–ї–Є–Љ–∞—В–Є—З–љ–∞ —В–µ–љ–і–µ–љ—Ж–Є—П –Ј–∞ –±—К–і–µ—Й–µ—В–Њ?
Nikor
–Э–∞ 30 —Б–µ–њ—В–µ–Љ–≤—А–Є 1928 –µ –Њ—В–Ї—А–Є—В –њ–µ–љ–Є—Ж–Є–ї–Є–љ—К—В
–Я—А–Њ—Б—В –І–Њ–≤–µ–Ї
–Э–Њ–≤–Њ –Њ–±—П—Б–љ–µ–љ–Є–µ –Ј–∞ –≥–Є–≥–∞–љ—В—Б–Ї–Є—В–µ –µ–Ї—Б–њ–ї–Њ–і–Є—А–∞—Й–Є –Ї—А–∞—В–µ—А–Є –≤ –°–Є–±–Є—А
dolivo
–Ъ–ї–Є–Љ–∞—В–Є—З–љ–Є—П—В —Б–Ї–µ–њ—В–Є—Ж–Є–Ј—К–Љ вАУ –љ–∞–є-—Б–Ї—К–њ–∞—В–∞ –ї—К–ґ–∞ –љ–∞ –љ–∞—И–µ—В–Њ –≤—А–µ–Љ–µ