

–Ч–∞ —Е–Њ—А–∞—В–∞, –Ї–Њ–Є—В–Њ –Љ—А–∞–Ј—П—В –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞ –Є —Б–µ¬†–њ–ї–∞—И–∞—В –Њ—В —Б–ї–Њ–ґ–љ–Є —Г—А–∞–≤–љ–µ–љ–Є—П, –Є–Ј—А–∞–Ј—К—В NP=P –µ –Є–Ј–Љ–∞–Љ–љ–Њ –њ—А–Њ—Б—В.
–Э–Њ –≤—К—А—Е—Г¬†–і–Њ–Ї–∞–Ј–∞—В–µ–ї—Б—В–≤–Њ—В–Њ –Љ—Г –Є–ї–Є –Ј–∞ –і–Њ–Ї–∞–Ј–≤–∞–љ–µ—В–Њ –љ–∞ –Њ–±—А–∞—В–љ–Њ—В–Њ (NP вЙ† P) —Б–∞ —А–∞–±–Њ—В–Є–ї–Є –±–µ–Ј—Г—Б–њ–µ—И–љ–Њ –і–µ—Б–µ—В–Ї–Є –≥–Њ–і–Є–љ–Є –љ–∞–є-–і–Њ–±—А–Є—В–µ —Г–Љ–Њ–≤–µ –љ–∞ –љ–∞—И–∞—В–∞ –њ–ї–∞–љ–µ—В–∞. –Ґ–Њ–≤–∞ –µ –µ–і–љ–∞ –Њ—В —Б–µ–і–µ–Љ—В–µ –Ј–∞–і–∞—З–Є –љ–∞ —Е–Є–ї—П–і–Њ–ї–µ—В–Є–µ—В–Њ, –Ј–∞ —З–Є–µ—В–Њ —А–µ—И–∞–≤–∞–љ–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—П—В –Є–љ—Б—В–Є—В—Г—В –Ъ–ї–µ–є –і–∞–≤–∞ –µ–і–Є–љ –Љ–Є–ї–Є–Њ–љ –і–Њ–ї–∞—А–∞.
–Э–µ—Й–Њ –њ–Њ–≤–µ—З–µ, –∞–Ї–Њ –љ—П–Ї–Њ–є —Г—Б–њ–µ–µ –Њ–±–Њ—Б–љ–Њ–≤–∞–љ–Њ –Є –Ї–∞—В–µ–≥–Њ—А–Є—З–љ–Њ –і–∞ –і–∞–і–µ –Њ—В–≥–Њ–≤–Њ—А, —З–µ NP –Є P —Б–∞ —А–∞–≤–љ–Є, —В–Њ–≤–∞ —Й–µ –њ—А–µ–Љ–∞—Е–љ–µ –≤—Б—П–Ї–∞–Ї–≤–Є –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П –њ—А–µ–і —З–Њ–≤–µ—И–Ї–Є—П —Г–Љ –Є –±–Є –Њ—В–≤–Њ—А–Є–ї–Њ –љ–µ–≤–µ—А–Њ—П—В–љ–Є –≤—К–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є –њ—А–µ–і –љ–∞—И–∞—В–∞ —Ж–Є–≤–Є–ї–Є–Ј–∞—Ж–Є—П.¬†
–Я—А–Њ—Б—В–Њ –Ї–∞–Ј–∞–љ–Њ
–Я—А–Њ—Б—В–Њ –Ї–∞–Ј–∞–љ–Њ, P —Б–∞ –≤—Б–Є—З–Ї–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ –ї–µ—Б–љ–Є –Ј–∞–і–∞—З–Є –Є NP –µ –љ–∞–±–Њ—А, –Ї–Њ–є—В–Њ –≤–Ї–ї—О—З–≤–∞ –Є–Ј–≥–ї–µ–ґ–і–∞—Й–Є –Љ–љ–Њ–≥–Њ, –Љ–љ–Њ–≥–Њ —В—А—Г–і–љ–Є –Ј–∞–і–∞—З–Є, —В–∞–Ї–∞ —З–µ –∞–Ї–Њ P = NP, —В–Њ–≤–∞ –±–Є –Њ–Ј–љ–∞—З–∞–≤–∞–ї–Њ, —З–µ –Њ—З–µ–≤–Є–і–љ–Њ —Б–ї–Њ–ґ–љ–Є –њ—А–Њ–±–ї–µ–Љ–Є –≤—Б—К—Й–љ–Њ—Б—В –Є–Љ–∞—В —Б—А–∞–≤–љ–Є—В–µ–ї–љ–Њ –ї–µ—Б–љ–Є —А–µ—И–µ–љ–Є—П.
–Т—К–њ—А–Њ—Б—К—В —Б–µ —Б–≤–µ–ґ–і–∞ –і–Њ: –Ј–∞–і—К–ї–ґ–Є—В–µ–ї–љ–Њ –ї–Є –µ –њ–Њ-–ї–µ—Б–љ–Њ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є –µ–і–љ–∞ –Ј–∞–і–∞—З–∞, –Њ—В–Ї–Њ–ї–Ї–Њ—В–Њ –і–∞ —Б–µ —А–µ—И–Є?
–†–∞–Ј–±–Є—А–∞ —Б–µ, –Є–Љ–∞ –љ—П–Ї–Њ–Є –њ–Њ–і—А–Њ–±–љ–Њ—Б—В–Є.
–Я–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ
–Х–і–Є–љ –Њ—В –љ–∞–є-–≤–∞–ґ–љ–Є—В–µ –≤—К–њ—А–Њ—Б–Є –≤¬†–Ї–Њ–Љ–њ—О—В—К—А–љ–Є—В–µ –љ–∞—Г–Ї–Є –µ¬†–Ї–Њ–ї–Ї–Њ –≤—А–µ–Љ–µ –µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ, –Ј–∞ –і–∞ —Б–µ –Є–Ј–њ—К–ї–љ–Є –і–∞–і–µ–љ –∞–ї–≥–Њ—А–Є—В—К–Љ. –Т—А–µ–Љ–µ—В–Њ –Ј–∞–≤–Є—Б–Є –Њ—В¬†–±—А–Њ—П –љ–∞ –µ–ї–µ–Љ–µ–љ—В–Є—В–µ –љ–∞ –∞–ї–≥–Њ—А–Є—В—К–Љ–∞, –Ї–Њ–Є—В–Њ —В—А—П–±–≤–∞ –і–∞ —Б–µ –Њ–±—А–∞–±–Њ—В—П—В.
–Я—А–µ–і—Б—В–∞–≤–µ—В–µ —Б–Є, –љ–∞–њ—А–Є–Љ–µ—А, —З–µ –Є–Љ–∞—В–µ –љ–µ—Б–Њ—А—В–Є—А–∞–љ —Б–њ–Є—Б—К–Ї —Б —З–Є—Б–ї–∞, –∞ –Є—Б–Ї–∞—В–µ –і–∞ –љ–∞–њ–Є—И–µ—В–µ –µ–і–Є–љ –∞–ї–≥–Њ—А–Є—В—К–Љ, –Ї–Њ–є—В–Њ –і–∞ –љ–∞–Љ–Є—А–∞ –љ–∞–є-–≥–Њ–ї—П–Љ–Њ—В–Њ. –Р–ї–≥–Њ—А–Є—В—К–Љ—К—В —В—А—П–±–≤–∞ –і–∞ —А–∞–Ј–≥–ї–µ–і–∞ –≤—Б–Є—З–Ї–Є —З–Є—Б–ї–∞ –≤ —Б–њ–Є—Б—К–Ї–∞ –Є –љ—П–Љ–∞ –Ї–∞–Ї —В–Њ–≤–∞ –і–∞ —Б–µ –Є–Ј–±–µ–≥–љ–µ. –Э–Њ –∞–Ї–Њ –њ—А–Њ—Б—В–Њ –Ј–∞–њ–Њ–Љ–љ—П –≤ —А–µ–≥–Є—Б—В—К—А –љ–∞–є-–≥–Њ–ї—П–Љ–Њ—В–Њ —З–Є—Б–ї–Њ, –Ї–Њ–µ—В–Њ –µ —Б—А–µ—Й–љ–∞–ї –і–Њ—Б–µ–≥–∞, –µ –і–Њ—Б—В–∞—В—К—З–љ–Њ –і–∞ –њ—А–Њ–≤–µ—А–Є –≤—Б–µ–Ї–Є –Ј–∞–њ–Є—Б —Б–∞–Љ–Њ –≤–µ–і–љ—К–ґ. –Я–Њ —В–Њ–Ј–Є –љ–∞—З–Є–љ –≤—А–µ–Љ–µ—В–Њ –Ј–∞ –Є–Ј–њ—К–ї–љ–µ–љ–Є–µ –љ–∞ –∞–ї–≥–Њ—А–Є—В—К–Љ–∞ –µ –њ—А–∞–≤–Њ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞ –±—А–Њ—П –љ–∞ –µ–ї–µ–Љ–µ–љ—В–Є—В–µ, —Б –Ї–Њ–Є—В–Њ —Б–µ —А–∞–±–Њ—В–Є. –Ь–Њ–ґ–µ –і–∞ –≥–Є –Њ–Ј–љ–∞—З–Є–Љ —Б N. –†–∞–Ј–±–Є—А–∞ —Б–µ, –њ–Њ–≤–µ—З–µ—В–Њ –∞–ї–≥–Њ—А–Є—В–Љ–Є —Б–∞ –њ–Њ-—Б–ї–Њ–ґ–љ–Є –Є –њ–Њ —В–Њ–Ј–Є –љ–∞—З–Є–љ –њ–Њ-–Љ–∞–ї–Ї–Њ –µ—Д–µ–Ї—В–Є–≤–љ–Є, –Њ—В–Ї–Њ–ї–Ї–Њ—В–Њ —В–Њ–Ј–Є, –љ—П–Ї–Њ–Є –∞–ї–≥–Њ—А–Є—В–Љ–Є –Є–Љ–∞—В –≤—А–µ–Љ–µ –Ј–∞ –Є–Ј–њ—К–ї–љ–µ–љ–Є–µ, –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞ N2¬†–љ–∞–њ—А–Є–Љ–µ—А.
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Є–Ј—А–∞–Ј, –Ї–Њ–є—В–Њ –≤–Ї–ї—О—З–≤–∞ –µ–ї–µ–Љ–µ–љ—В–Є, –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Є –љ–∞ N, N2¬†–Є N –љ–∞ –љ—П–Ї–∞–Ї–≤–∞ –і—А—Г–≥–∞ —Б—В–µ–њ–µ–љ, —Б–µ –љ–∞—А–Є—З–∞ –њ–Њ–ї–Є–љ–Њ–Љ –Є —В–Њ–≤–∞ –Њ–Ј–љ–∞—З–∞–≤–∞ "P"-—В–Њ –≤ вАЬP = NPвАЭ. P –µ –љ–∞–±–Њ—А –Њ—В –Ј–∞–і–∞—З–Є, —З–Є–µ—В–Њ –≤—А–µ–Љ–µ –Ј–∞ —А–µ—И–∞–≤–∞–љ–µ –µ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞ –њ–Њ–ї–Є–љ–Њ–Љ —Б —З–ї–µ–љ–Њ–≤–µ N, N2 –Є —В.–љ.
–Ю—З–µ–≤–Є–і–љ–Њ –µ, —З–µ –µ–і–Є–љ –∞–ї–≥–Њ—А–Є—В—К–Љ, —З–Є–µ—В–Њ –≤—А–µ–Љ–µ –Ј–∞ –Є–Ј–њ—К–ї–љ–µ–љ–Є–µ –µ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞¬†N3, –µ –њ–Њ-–±–∞–≤–µ–љ, –Њ—В–Ї–Њ–ї–Ї–Њ—В–Њ —В–∞–Ї—К–≤, —З–Є–µ—В–Њ –≤—А–µ–Љ–µ –Ј–∞ –Є–Ј–њ—К–ї–љ–µ–љ–Є–µ –µ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞ N. –Э–Њ —В–µ–Ј–Є —А–∞–Ј–ї–Є–Ї–Є —Б–∞ –љ–µ–Ј–љ–∞—З–Є—В–µ–ї–љ–Є –≤ —Б—А–∞–≤–љ–µ–љ–Є–µ —Б —А–∞–Ј–ї–Є–Ї–∞—В–∞ –Љ–µ–ґ–і—Г –њ–Њ–ї–Є–љ–Њ–Љ–љ–Є –Є–Ј—А–∞–Ј–Є - –Ї—К–і–µ—В–Њ N —Б–µ –њ–Њ–≤–і–Є–≥–∞ –љ–∞ —З–Є—Б–ї–Њ–≤–Є —Б—В–µ–њ–µ–љ - –Є –Є–Ј—А–∞–Ј–Є, –њ—А–Є –Ї–Њ–Є—В–Њ —З–Є—Б–ї–Њ —Б–µ –Є–Ј–і–Є–≥–∞ –љ–∞ N-—В–∞ —Б—В–µ–њ–µ–љ, –Ї–∞—В–Њ –љ–∞–њ—А–Є–Љ–µ—А 2N.
–Р–Ї–Њ –∞–ї–≥–Њ—А–Є—В—К–Љ, —З–Є–µ—В–Њ –≤—А–µ–Љ–µ¬†–Ј–∞ –Є–Ј–њ—К–ї–љ–µ–љ–Є–µ –µ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞ N, –Є–Ј–≤—К—А—И–≤–∞ –Є–Ј—З–Є—Б–ї–µ–љ–Є—П—В–∞ —Б–Є –Ј–∞ 100 –µ–ї–µ–Љ–µ–љ—В–∞ –Ј–∞ —Б–µ–Ї—Г–љ–і–Є, –∞–ї–≥–Њ—А–Є—В—К–Љ, —З–Є–µ—В–Њ –≤—А–µ–Љ–µ –Ј–∞ –Є–Ј–њ—К–ї–љ–µ–љ–Є–µ –µ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞ N3 —А–∞–±–Њ—В–Є –њ–Њ—З—В–Є —В—А–Є —З–∞—Б–∞. –Э–Њ –Ј–∞ –∞–ї–≥–Њ—А–Є—В—К–Љ, —З–Є–µ—В–Њ –≤—А–µ–Љ–µ –Ј–∞ –Є–Ј–њ—К–ї–љ–µ–љ–Є–µ¬†–µ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Њ –љ–∞ 2N, –Љ—Г —В—А—П–±–≤–∞—В 300 –Ї–≤–Є–љ—В–Є–ї–Є–Њ–љ –≥–Њ–і–Є–љ–Є. –Ш –њ–Њ–ї–Њ–ґ–µ–љ–љ–Є–µ—В–Њ —Б—В–∞–≤–∞ –Љ–љ–Њ–≥–Њ, –Љ–љ–Њ–≥–Њ –њ–Њ-–ї–Њ—И–Њ —Б –љ–∞—А–∞—Б—В–≤–∞–љ–µ—В–Њ –љ–∞ N. –Т—К–Ј–Љ–Њ–ґ–љ–Њ –µ –≤—А–µ–Љ–µ—В–Њ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞ –і–∞ –љ–µ –љ–Є —Б—В–Є–≥–љ–µ.
–Ґ–∞–Ї–∞ —З–µ –≤—К–њ—А–Њ—Б—К—В "P —А–∞–≤–љ–Њ –ї–Є –µ –љ–∞ NP?" –Њ–Ј–љ–∞—З–∞–≤–∞ "–Р–Ї–Њ —А–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –њ—А–Њ–±–ї–µ–Љ–∞ –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є –≤ –њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ, –Љ–Њ–ґ–µ –ї–Є –і–∞ —Б–µ –љ–∞–Љ–µ—А–Є –Ј–∞ –њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ?".
–Ъ–∞–Ј–∞–љ–Њ –њ–Њ-–њ—А–Њ—Б—В–Њ: –Ј–∞–і—К–ї–ґ–Є—В–µ–ї–љ–Њ –ї–Є¬†–µ –њ–Њ-–ї–µ—Б–љ–Њ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є –µ–і–љ–∞ –Ј–∞–і–∞—З–∞, –Њ—В–Ї–Њ–ї–Ї–Њ—В–Њ –і–∞ —Б–µ —А–µ—И–Є?
–Я—А–Є–Љ–µ—А–Є
–Т –Њ–±—Й–Є –ї–Є–љ–Є–Є –Љ–Њ–ґ–µ –і–∞ —Б–µ –Ї–∞–ґ–µ, —З–µ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –µ —А–µ—И–Є–Љ–Њ –≤ –њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ, –µ —А–µ—И–Є–Љ–Њ –Њ—В –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–∞ –≥–ї–µ–і–љ–∞ —В–Њ—З–Ї–∞, –∞ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ —Б–µ —А–µ—И–∞–≤–∞ –≤ –µ–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ, –Ј–∞ –љ–µ—В—А–Є–≤–Є–∞–ї–љ–Є –њ—А–Є–Љ–µ—А–Є, –Љ–Њ–ґ–µ –і–∞ –љ–µ —Г—Б–њ–µ–µ–Љ –і–∞ —А–µ—И–Є–Љ –њ—А–µ–і–Є –Ї—А–∞—П –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞.
–Э–∞–Љ–Є—А–∞–љ–µ –љ–∞ –і–µ–ї–Є—В–µ–ї–Є –љ–∞ 13717421 –µ –Љ–љ–Њ–≥–Њ —Б–ї–Њ–ґ–љ–Њ, –љ–Њ –Љ–љ–Њ–≥–Њ –ї–µ—Б–љ–Њ –µ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є, —З–µ 3607 x 3808 = 13717421. –Ґ–Њ–≤–∞ –µ –≤ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –њ–Њ–≤–µ—З–µ—В–Њ –≤–Є–і–Њ–≤–µ –Ї—А–Є–њ—В–Є—А–∞–љ–µ: –Љ–љ–Њ–≥–Њ —В—А—Г–і–љ–Њ –і–∞ —Б–µ —А–∞–Ј—З–µ—В–µ, –љ–Њ –ї–µ—Б–љ–Њ –Ј–∞ –њ—А–Њ–≤–µ—А–Ї–∞. –Ґ–Њ–≤–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ –Њ—З–µ–≤–Є–і–љ–Њ, –љ–Њ –љ–Є–Ї–Њ–є –љ–µ –Љ–Њ–ґ–µ –і–Њ—Б–µ–≥–∞ –і–∞ –≥–Њ –і–Њ–Ї–∞–ґ–µ.
–Ю—Й–µ –µ–і–Є–љ –њ—А–Є–Љ–µ—А - –≤—П—А–љ–Њ –ї–Є –µ, —З–µ —Б—А–µ–і —З–Є—Б–ї–∞—В–∞ {вИТ2, вИТ3, 15, 14, 7, вИТ10, вА¶} –Є–Љ–∞ —В–∞–Ї–Є–≤–∞, —З–Є—П—В–Њ —Б—Г–Љ–∞ –µ —А–∞–≤–љ–∞ –љ–∞ 0? –Ю—В–≥–Њ–≤–Њ—А—К—В –µ –і–∞, –Ј–∞—Й–Њ—В–Њ вИТ2 вИТ3 + 15 вИТ10 = 0 . –Ґ–Њ–Ј–Є¬†–Њ—В–≥–Њ–≤–Њ—А –ї–µ—Б–љ–Њ —Б–µ –њ—А–Њ–≤–µ—А—П–≤–∞ - —В—А—П–±–≤–∞ —Б–∞–Љ–Њ –і–∞ —Б—К–±–µ—А–µ–Љ —З–Є—Б–ї–∞—В–∞. –°–ї–µ–і–≤–∞ –ї–Є –Њ—В —В–Њ–≤–∞, —З–µ —Б—К—Й–Њ —В–Њ–ї–Ї–Њ–≤–∞ –ї–µ—Б–љ–Њ —Б–µ –љ–∞–Љ–Є—А–∞ –Ї–Њ–Є —Б–∞ —В–µ–Ј–Є —З–Є—Б–ї–∞? –Ф–∞–ї–Є –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є —Б–µ—А—В–Є—Д–Є–Ї–∞—В–∞ (–Є–љ—Д–Њ—А–Љ–∞—Ж–Є—П—В–∞, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–∞ –Ј–∞ –њ—А–Њ–≤–µ—А–Ї–∞ –љ–∞ –њ–Њ–ї–Њ–ґ–Є—В–µ–ї–љ–Є—П –Њ—В–≥–Њ–≤–Њ—А) –µ —Б—К—Й–Њ —В–Њ–ї–Ї–Њ–≤–∞ –ї–µ—Б–љ–Њ, –Ї–∞–Ї—В–Њ –і–∞ —Б–µ –љ–∞–Љ–µ—А–Є? –Ш–Ј–≥–ї–µ–ґ–і–∞, —З–µ –і–∞ —Б–µ –љ–∞–Љ–µ—А—П—В —З–Є—Б–ї–∞—В–∞ –µ –њ–Њ-—Б–ї–Њ–ґ–љ–Њ, –љ–Њ —В–Њ–≤–∞ –љ–µ –µ –і–Њ–Ї–∞–Ј–∞–љ–Њ.
–Х—В–Њ –Њ—Й–µ –µ–і–Є–љ –њ—А–Є–Љ–µ—А, –Є–ї—О—Б—В—А–Є—А–∞—Й –Ј–∞–і–∞—З–∞—В–∞, –Ї–Њ–є—В–Њ –і–∞–≤–∞ –љ–∞ —Б—В—А–∞–љ–Є—Ж–∞—В–∞ —Б–Є –Ш–љ—Б—В–Є—В—Г—В—К—В –Ъ–ї–µ–є:
–Ф–∞ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–Є–Љ, —З–µ –Њ—А–≥–∞–љ–Є–Ј–Є—А–∞—В–µ –љ–∞—Б—В–∞–љ—П–≤–∞–љ–µ—В–Њ –≤ –ґ–Є–ї–Є—Й–∞ –љ–∞ –≥—А—Г–њ–∞ –Њ—В 400¬†—Б—В—Г–і–µ–љ—В–Є. –Ь–µ—Б—В–∞—В–∞ —Б–∞ –Њ–≥—А–∞–љ–Є—З–µ–љ–Є –Є —Б–∞–Љ–Њ 100¬†–Њ—В —Б—В—Г–і–µ–љ—В–Є—В–µ —Й–µ –њ–Њ–ї—Г—З–∞—В –Љ–µ—Б—В–∞ –≤ –і–≤–Њ–є–љ–∞ —Б—В–∞—П –≤ –Њ–±—Й–µ–ґ–Є—В–Є–µ—В–Њ. –Э–µ—Й–∞—В–∞ —Б–µ —Г—Б–ї–Њ–ґ–љ—П–≤–∞—В, –Ј–∞—Й–Њ—В–Њ –і–µ–Ї–∞–љ—К—В –µ –њ—А–µ–і–Њ—Б—В–∞–≤–Є–ї —Б–њ–Є—Б—К–Ї –љ–∞ –љ–µ—Б—К–≤–Љ–µ—Б—В–Є–Љ–Є –і–≤–Њ–є–Ї–Є —Б—В—Г–і–µ–љ—В–Є, –Ї–Њ–Є—В–Њ –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б–∞ –≤ –µ–і–љ–∞ –Є —Б—К—Й–∞ —Б—В–∞—П. –Ы–µ—Б–љ–Њ –µ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є –і–∞–ї–Є –і–∞–і–µ–љ–∞ –Є–Ј–±—А–∞–љ–∞ –≥—А—Г–њ–∞ –Њ—В —Б—В–Њ —Б—В—Г–і–µ–љ—В–Є –µ –Ј–∞–і–Њ–≤–Њ–ї–Є—В–µ–ї–љ–∞ (—В.–µ. –љ—П–Љ–∞ –і–≤–Њ–є–Ї–∞ –≤ —Б–њ–Є—Б—К–Ї–∞, –Ї–Њ—П—В–Њ –і–∞ –µ –≤–Ї–ї—О—З–µ–љ–∞ –Є –≤ —Б–њ–Є—Б—К–Ї–∞ –љ–∞ –і–µ–Ї–∞–љ–∞), –Њ–±–∞—З–µ –Ј–∞–і–∞—З–∞—В–∞ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ —В–∞–Ї—К–≤ —Б–њ–Є—Б—К–Ї –Њ—В –љ—Г–ї–∞—В–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ —В–Њ–ї–Ї–Њ–≤–∞ —В—А—Г–і–љ–∞, –Ї–Њ–ї–Ї–Њ—В–Њ –Є –љ–∞–њ—К–ї–љ–Њ –љ–µ–њ—А–∞–Ї—В–Є—З–љ–∞. –Т—Б—К—Й–љ–Њ—Б—В –Њ–±—Й–Є—П—В –±—А–Њ–є –≤–∞—А–Є–∞–љ—В–Є –Ј–∞ –Є–Ј–±–Њ—А –љ–∞ —Б—В–Њ –Њ—В —З–µ—В–Є—А–Є—Б—В–Њ—В–Є–љ –Ј–∞—П–≤–Ї–Є –µ –њ–Њ-–≥–Њ–ї—П–Љ –Њ—В –±—А–Њ—П –љ–∞ –∞—В–Њ–Љ–Є—В–µ –≤ –њ–Њ–Ј–љ–∞—В–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞! –Я–Њ —В–Њ–Ј–Є –љ–∞—З–Є–љ –≤ –±—К–і–µ—Й–µ —Ж–Є–≤–Є–ї–Є–Ј–∞—Ж–Є—П—В–∞ –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –љ–∞–і—П–≤–∞ –і–∞ –Є–Ј–≥—А–∞–і–Є —Б—Г–њ–µ—А–Ї–Њ–Љ–њ—О—В—К—А, –Ї–Њ–є—В–Њ –і–∞ –Љ–Њ–ґ–µ –і–∞ —А–µ—И–Є –њ—А–Њ–±–ї–µ–Љ–∞ —Б –≥—А—Г–±–∞ —Б–Є–ї–∞ - —В–Њ–µ—Б—В —З—А–µ–Ј –њ—А–Њ–≤–µ—А–Ї–∞ –љ–∞ –≤—Б—П–Ї–∞ –≤—К–Ј–Љ–Њ–ґ–љ–∞ –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П –Њ—В 100 —Б—В—Г–і–µ–љ—В–Є.
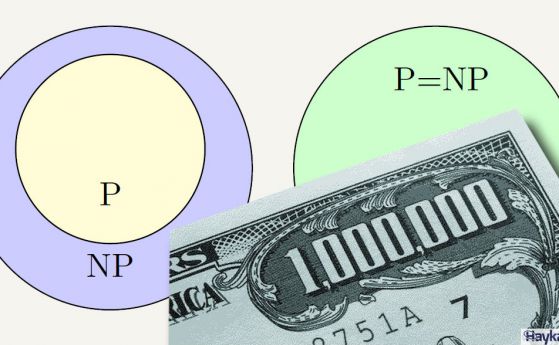
–Ъ–ї–∞—Б–Њ–≤–µ—В–µ¬†P –Є NP
–Ъ—А–∞—В–Ї–Њ –Є –њ—А–Њ—Б—В–Њ –Љ–Њ–ґ–µ –Ї–ї–∞—Б–Њ–≤–µ—В–µ P –Є NP –і–∞ —Б–µ –Њ–њ–Є—И–∞—В –њ–Њ —Б–ї–µ–і–љ–Є—П –љ–∞—З–Є–љ: P¬†—Б–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–Є –Ј–∞–і–∞—З–Є, –Ї–Њ–Є—В–Њ –ї–µ—Б–љ–Њ —Б–µ —А–µ—И–∞–≤–∞—В; NP - –Ј–∞–і–∞—З–Є, –Ј–∞ –Ї–Њ–Є—В–Њ –µ –ї–µ—Б–љ–Њ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є –і–∞–ї–Є —В–≤—К—А–і–µ–љ–Є–µ—В–Њ –µ –њ—А–∞–≤–Є–ї–љ–Њ.¬†
–Т—Б–Є—З–Ї–Є –њ–Њ–Љ–љ–Є–Љ –Њ—В –і–µ—В—Б—В–≤–Њ—В–Њ —Б–Є –Ї–≤–∞–і—А–∞—В–љ–Є—В–µ —Г—А–∞–≤–љ–µ–љ–Є—П, –Ї–Њ–Є—В–Њ —Б–µ —А–µ—И–∞–≤–∞—В —Б¬†–і–Є—Б–Ї—А–Є–Љ–Є–љ–∞–љ—В–∞ (—В–µ–Ј–Є, –Ї–Њ–Є—В–Њ –љ–µ –њ–Њ–Љ–љ—П—В - –і–∞ –њ–Њ–≥–ї–µ–і–љ–∞—В –њ–Њ-–і–Њ–ї—Г). –†–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –Ј–∞–і–∞—З–∞—В–∞ —Б–µ –Њ—В–љ–∞—Б—П¬†–Ї—К–Љ –Ї–ї–∞—Б P (Polynomial time) - –Ј–∞ –љ–µ—П –Є–Љ–∞ –±—К—А–Ј (—В—Г–Ї –њ–Њ–і "–±—К—А–Ј" —Б–µ —А–∞–Ј–±–Є—А–∞, —З–µ —Б–µ –Є–Ј–њ—К–ї–љ—П–≤–∞ –Ј–∞ –њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ) –∞–ї–≥–Њ—А–Є—В—К–Љ –Ј–∞ —А–µ—И–∞–≤–∞–љ–µ:
*–Ъ–≤–∞–і—А–∞—В–љ–Њ—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Љ–∞ —Б–ї–µ–і–љ–Є—П –≤–Є–і: ax2 + bx + c = 0
–Ї—К–і–µ—В–Њ a,b,c —Б–∞ —А–µ–∞–ї–љ–Є —З–Є—Б–ї–∞ –Є a вЙ† 0. –Т—Б—П–Ї–Њ –Ї–≤–∞–і—А–∞—В–љ–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Љ–Њ–ґ–µ –і–∞ –Є–Љ–∞ 0, 1 –Є–ї–Є 2 —А–µ–∞–ї–љ–Є –Ї–Њ—А–µ–љ–∞,
–њ–Њ–ї—Г—З–µ–љ–Є –њ–Њ —Б–ї–µ–і–љ–∞—В–∞ —Д–Њ—А–Љ—Г–ї–∞:

–І–Є—Б–ї–Њ—В–Њ D = b2 - 4ac —Б–µ –љ–∞—А–Є—З–∞ –і–Є—Б–Ї—А–Є–Љ–Є–љ–∞–љ—В–∞.¬†–Р–Ї–Њ¬†D < 0, –Ї–≤–∞–і—А–∞—В–љ–Њ—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –љ—П–Љ–∞ —А–µ–∞–ї–љ–Є –Ї–Њ—А–µ–љ–Є. –Р–Ї–Њ¬†D = 0, —Г—А–∞–≤–љ–µ–љ–Є–µ—В–Њ –Є–Љ–∞ 1 —А–µ–∞–ї–µ–љ –Ї–Њ—А–µ–љ - x=вИТb/2a. –Р–Ї–Њ D > 0, –Ї–≤–∞–і—А–∞—В–љ–Њ—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ –Є–Љ–∞ 2 —А–µ–∞–ї–љ–Є –Ї–Њ—А–µ–љ–∞.
–°—К—Й–µ—Б—В–≤—Г–≤–∞—В –Є NP-–Ј–∞–і–∞—З–Є (Non-deterministic Polynomial time - –Ї–Њ–µ—В–Њ –Њ–Ј–љ–∞—З–∞–≤–∞ –љ–µ–і–µ—В–µ—А–Љ–Є–љ–Є—А–∞–љ–Њ –њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ), –љ–∞–Љ–µ—А–µ–љ–Њ—В–Њ —А–µ—И–µ–љ–Є–µ –љ–∞ –Ї–Њ–Є—В–Њ –Љ–Њ–ґ–µ –±—К—А–Ј–Њ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А–Є –њ–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ –∞–ї–≥–Њ—А–Є—В—К–Љ - —В–Њ–µ—Б—В —А–µ—И–µ–љ–Є—П—В–∞ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –њ—А–Њ–≤–µ—А–µ–љ–Є –Ј–∞ –њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ.
–Р–Ї–Њ —Б–µ –≤—К—А–љ–µ–Љ –Ї—К–Љ —А–µ—И–∞–≤–∞–љ–µ—В–Њ –љ–∞ –Ї–≤–∞–і—А–∞—В–љ–Њ—В–Њ —Г—А–∞–≤–љ–µ–љ–Є–µ, –≤–Є–ґ–і–∞–Љ–µ, —З–µ –≤ —В–Њ–Ј–Є –њ—А–Є–Љ–µ—А —Б—К—Й–µ—Б—В–≤—Г–≤–∞—Й–Є—П—В –∞–ї–≥–Њ—А–Є—В—К–Љ –Ј–∞ —А–µ—И–∞–≤–∞–љ–µ —Б–µ –њ—А–Њ–≤–µ—А—П–≤–∞ —Б—К—Й–Њ —В–∞–Ї–∞ –ї–µ—Б–љ–Њ –Є –±—К—А–Ј–Њ, –Ї–∞–Ї—В–Њ —Б–µ –Є —А–µ—И–∞–≤–∞. –Ґ–Њ–≤–∞ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ —В–∞–Ј–Є –Ј–∞–і–∞—З–∞ —Б–µ –Њ—В–љ–∞—Б—П –Є –Ї—К–Љ –њ—К—А–≤–Є—П –Ї–ї–∞—Б, –Є –Ї—К–Љ –≤—В–Њ—А–Є—П.
–Ъ–ї–∞—Б—К—В P¬†–µ –њ–Њ–і–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –љ–∞ –Ї–ї–∞—Б¬†NP –Є–ї–Є –Ї–∞–Ї—В–Њ –±–Є—Е–∞ –Ї–∞–Ј–∞–ї–Є –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є—В–µ -¬†P вКВ NP:
 P вКВ NP (–Я—А–Њ–±–ї–µ–Љ–Є—В–µ P —Б–∞ –њ–Њ–і–≤–Є–і –љ–∞ –њ—А–Њ–±–ї–µ–Љ–Є—В–µ NP)
P вКВ NP (–Я—А–Њ–±–ї–µ–Љ–Є—В–µ P —Б–∞ –њ–Њ–і–≤–Є–і –љ–∞ –њ—А–Њ–±–ї–µ–Љ–Є—В–µ NP)
–Ф–Њ—Б–µ–≥–∞ –љ–Є–Ї–Њ–є –љ–µ –Љ–Њ–ґ–µ –і–∞ –і–Њ–Ї–∞–ґ–µ –Є–ї–Є –Њ—В—А–µ—З–µ —Б—В—А–Њ–≥–Њ—Б—В—В–∞ –љ–∞ —В–Њ–≤–∞ –≤–Ї–ї—О—З–≤–∞–љ–µ, —Б –і—А—Г–≥–Є –і—Г–Љ–Є, –і–∞ –љ–∞–Љ–µ—А–Є –∞–ї–≥–Њ—А–Є—В—К–Љ, –Ї–Њ–є—В–Њ —Б–µ –љ–∞–Љ–Є—А–∞ –≤ –Ї–ї–∞—Б–∞ NP, –љ–Њ –љ–µ –њ—А–Є–љ–∞–і–ї–µ–ґ–Є –Ї—К–Љ P (—В.–µ. –µ –≤ –ґ—К–ї—В–∞—В–∞ —З–∞—Б—В –љ–∞ —Б—Е–µ–Љ–∞—В–∞). –Ю—В–≥–Њ–≤–Њ—А—К—В –і–∞–ї–Є¬†¬†P = NP —Й–µ –Њ–њ—А–µ–і–µ–ї–Є –і–∞–ї–Є –Ј–∞–і–∞—З–Є—В–µ, –Ї–Њ–Є—В–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –њ—А–Њ–≤–µ—А–µ–љ–Є –≤ –њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ, —Б—К—Й–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В —А–µ—И–µ–љ–Є –≤ –њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ.
NP-–њ—К–ї–љ–Є—В–µ –Ј–∞–і–∞—З–Є
–Р–Ї–Њ —Б–µ –Њ–Ї–∞–ґ–µ, —З–µ P вЙ† NP , —В–Њ–≤–∞ –±–Є –Њ–Ј–љ–∞—З–∞–≤–∞–ї–Њ, —З–µ –Є–Љ–∞ –Ј–∞–і–∞—З–Є –≤ NP, –Ї–Њ–Є—В–Њ –µ¬†–њ–Њ-—В—А—Г–і–љ–Њ –і–∞ —Б–µ –Є–Ј—З–Є—Б–ї—П—В, –Њ—В–Ї–Њ–ї–Ї–Њ—В–Њ –і–∞ —Б–µ –њ—А–Њ–≤–µ—А—П—В¬†- —В–µ –љ–µ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В —А–µ—И–µ–љ–Є –≤ –њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ, –љ–Њ –Њ—В–≥–Њ–≤–Њ—А—К—В –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –њ—А–Њ–≤–µ—А–µ–љ –≤ –њ–Њ–ї–Є–љ–Њ–Љ–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ.¬†
–Ґ–∞–Ї–Є–≤–∞¬†—Б–∞ —В. –љ–∞—А. NP-–њ—К–ї–љ–Є¬†(NP-Complete) –Ј–∞–і–∞—З–Є. –Ю—В –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П—В–∞ –љ–∞ –Ї–ї–∞—Б–Њ–≤–µ—В–µ —Б–ї–µ–і–≤–∞, —З–µ –Ї–ї–∞—Б P –µ –Ї–ї–∞—Б—К—В –љ–∞ –љ–∞–є-–ї–µ—Б–љ–Є—В–µ –Ј–∞–і–∞—З–Є –≤ NP. –Ъ–ї–∞—Б—К—В –љ–∞ NP-–њ—К–ї–љ–Є—В–µ –Ј–∞–і–∞—З–Є –µ –љ–∞–є-—Б–ї–Њ–ґ–µ–љ.
NP-–њ—К–ї–љ–Є—В–µ –Ј–∞–і–∞—З–Є —Б–µ —А–µ—И–∞–≤–∞—В –Ј–∞ –µ–Ї—Б–њ–Њ–љ–µ–љ—Ж–Є–∞–ї–љ–Њ –≤—А–µ–Љ–µ (–Є–ї–Є –Ј–∞ –≤—А–µ–Љ–µ n!) –Є —В–Њ–≤–∞ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –Љ–љ–Њ–≥–Њ, –Љ–љ–Њ–≥–Њ –і—К–ї–≥–Њ. –Ґ–∞–Ї–Є–≤–∞ —Б–∞ –Є–Ј–±—А–Њ–µ–љ–Є—В–µ –≤ –љ–∞—З–∞–ї–Њ—В–Њ¬†–њ—А–Є–Љ–µ—А–Є. –Ч–∞ –Љ–∞–ї–Ї–Є —Б—В–Њ–є–љ–Њ—Б—В–Є –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ —В–µ —Б–µ —А–µ—И–µ–≤–∞—В —Б—А–∞–≤–љ–Є—В–µ–ї–љ–Њ –±—К—А–Ј–Њ, –љ–Њ –њ–Њ—Б–ї–µ –±—К—А–Ј–Њ –љ–∞—А–∞—Б—В–≤–∞—В. –Ш –∞–Ї–Њ –љ–∞ 21 –µ –ї–µ—Б–љ–Њ –і–∞ —Б–µ –љ–∞–Љ–µ—А—П—В –і–µ–ї–Є—В–µ–ї–Є—В–µ, —В–Њ –Ј–∞ 13717421 –µ –Љ–љ–Њ–≥–Њ –њ–Њ-—В—А—Г–і–љ–Њ.¬†–†–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –Ј–∞–і–∞—З–∞—В–∞ –Ј–∞ 8-—В–µ —Ж–∞—А–Є—Ж–Є, –Ї–Њ–Є—В–Њ –љ–µ —Б–µ –Ј–∞—Б—В—А–∞—И–∞–≤–∞—В –≤–Ј–∞–Є–Љ–љ–Њ –Ј–∞ —Б—В–∞–љ–і–∞—А—В–љ–∞—В–∞ —И–∞—Е–Љ–∞—В–љ–∞ –і—К—Б–Ї–∞, –µ –Њ—В–Ї—А–Є—В–Њ –њ–Њ—З—В–Є –≤–µ–і–љ–∞–≥–∞ —Б–ї–µ–і –њ—Г–±–ї–Є–Ї—Г–≤–∞–љ–µ—В–Њ –љ–∞ –Ј–∞–і–∞—З–∞—В–∞, –љ–Њ —Б —Г–≤–µ–ї–Є—З–∞–≤–∞–љ–µ—В–Њ –љ–∞ —А–∞–Ј–Љ–µ—А–∞ –љ–∞ –і—К—Б–Ї–∞—В–∞ –Є –±—А–Њ—П –љ–∞ —Д–Є–≥—Г—А–Є—В–µ —В—К—А—Б–µ–љ–µ—В–Њ –љ–∞ —А–µ—И–µ–љ–Є–µ —Б—В–∞–љ–∞ –њ–Њ-—Б–ї–Њ–ґ–љ–Њ.¬†–Ч–∞ 27 —Ж–∞—А–Є—Ж–Є –Є –і—К—Б–Ї–∞ 27—Е27 –±—А–Њ—П—В –љ–∞ —А–µ—И–µ–љ–Є—П—В–∞ –µ –њ–Њ–≤–µ—З–µ –Њ—В 2.34 * 10 17, –∞ –Ј–∞ –і—К—Б–Ї–∞ 1000—Е1000 –љ–Є–Ї–Њ—П —Б—К–≤—А–µ–Љ–µ–љ–љ–∞ –Љ–∞—И–Є–љ–∞ –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ —Б–њ—А–∞–≤–Є.
–Ґ–∞–Ї–∞¬†NP-–њ—К–ї–љ–Є—В–µ –Ј–∞–і–∞—З–Є¬†—Д–Њ—А–Љ–Є—А–∞—В –≤ –Њ–њ—А–µ–і–µ–ї–µ–љ —Б–Љ–Є—Б—К–ї –њ–Њ–і–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –Њ—В "—Б—В–∞–љ–і–∞—А—В–љ–Є—В–µ" –Ј–∞–і–∞—З–Є¬†–≤ –Ї–ї–∞—Б NP. –Р–Ї–Њ –Ј–∞ –љ—П–Ї–Њ–Є –Њ—В —В—П—Е —Б–µ –љ–∞–Љ–µ—А–Є "–њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –±—К—А–Ј" –∞–ї–≥–Њ—А–Є—В—К–Љ –Ј–∞ —А–µ—И–µ–љ–Є–µ, —В–Њ–≥–∞–≤–∞ –Ј–∞ –≤—Б—П–Ї–∞ –і—А—Г–≥–∞ –Ј–∞–і–∞—З–∞ –Њ—В NP –Ї–ї–∞—Б–∞ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ —А–µ—И–µ–љ–∞ —В–Њ—З–љ–Њ —В–Њ–ї–Ї–Њ–≤–∞ –±—К—А–Ј–Њ.¬†

NPC вКВ NP (–Ї—К–і–µ—В–Њ NPC -¬†NP-Complete -¬†NP-–њ—К–ї–љ–Є –Ј–∞–і–∞—З–Є).¬†–Э–∞ —Б—Е–µ–Љ–∞—В–∞ –Ї–ї–∞—Б–Њ–≤–µ—В–µ –† –Є NPC –љ–µ —Б–µ –њ—А–µ—Б–Є—З–∞—В:
NPC вИ© P = вИЕ
–Ъ–∞–Ї–≤–Њ –±–Є —Б—В–∞–љ–∞–ї–Њ, –∞–Ї–Њ —Б–µ¬†–і–Њ–Ї–∞–ґ–µ, —З–µ P = NP
–Ъ–∞–Ї–≤–Њ –±–Є —Б—В–∞–љ–∞–ї–Њ, –∞–Ї–Њ –Ї–ї–∞—Б P –Є –Ї–ї–∞—Б NPC —Б–µ¬†–њ—А–µ—Б–Є—З–∞—В? –Я–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Ї—К–Љ NP-–њ—К–ї–љ–∞—В–∞ –Ј–∞–і–∞—З–∞ –Љ–Њ–ґ–µ –і–∞ —Б–µ —Б–≤–µ–і–µ¬†–≤—Б—П–Ї–∞ –Ј–∞–і–∞—З–∞ –Њ—В –Ї–ї–∞—Б NP. –°–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ, –∞–Ї–Њ –њ–Њ–љ–µ –Ј–∞ –µ–і–љ–∞ –Њ—В —В—П—Е —Б–µ –љ–∞–Љ–µ—А–Є –∞–ї–≥–Њ—А–Є—В—К–Љ –Ј–∞ —А–µ—И–µ–љ–Є–µ –Ј–∞ –њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ - —В–Њ–≤–∞ —Й–µ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ –њ—А–Њ–±–ї–µ–Љ—К—В –µ —А–µ—И–µ–љ.
–Э–Њ¬†–∞–Ї–Њ —З–Њ–≤–µ—З–µ—Б—В–≤–Њ—В–Њ —Б–µ –љ–∞—Г—З–Є –і–∞ —А–µ—И–∞–≤–∞ –±—К—А–Ј–Њ NP-–њ—К–ї–љ–Є¬†–Ј–∞–і–∞—З–Є (–≤ –њ–Њ–ї–Є–љ–Њ–Љ–љ–Њ –≤—А–µ–Љ–µ), –њ–Њ—Б–ї–µ–і—Б—В–≤–Є—П—В–∞ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –Љ–љ–Њ–≥–Њ –љ–µ–њ—А–Є—П—В–љ–Є. –Я—А–∞–Ї—В–Є—З–µ—Б–Ї–∞—В–∞ –Ї—А–Є–њ—В–Њ–≥—А–∞—Д–Є—П –≤ –њ–Њ-–≥–Њ–ї—П–Љ–∞—В–∞ —Б–Є —З–∞—Б—В —Й–µ —Б—В–∞–љ–µ –±–µ–Ј–њ–Њ–ї–µ–Ј–љ–∞. –¶—П–ї–∞—В–∞ –Ј–∞—Й–Є—В–µ–љ–∞ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—П (–љ–∞–њ—А–Є–Љ–µ—А –њ–∞—А–Њ–ї–∞—В–∞ –≤–Є –Ј–∞ –±–∞–љ–Ї–Њ–≤–∞—В–∞ –≤–Є —Б–Љ–µ—В–Ї–∞) —Й–µ –±—К–і–µ –љ–∞–њ—К–ї–љ–Њ "–±–µ–Ј–Ј–∞—Й–Є—В–љ–∞".
–Р–Ї–Њ —Б–µ –і–Њ–Ї–∞–ґ–µ —А–∞–≤–µ–љ—Б—В–≤–Њ—В–Њ P = NP, —Ж—П–ї–∞—В–∞ –є–µ—А–∞—А—Е–Є—П –Ї–ї–∞—Б–Њ–≤–µ —Й–µ —Б–µ –њ–Њ–±–µ—А–µ –≤ –µ–і–Є–љ –Ї–ї–∞—Б P. –Я–Њ–ї–Ј–Є—В–µ —Б—К—Й–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –Њ–≥—А–Њ–Љ–љ–Є. –©–µ —Б–µ –љ–∞—Г—З–Є–Љ –і–∞ –њ—А–µ—Б–Љ—П—В–∞–Љ–µ¬†–±—К—А–Ј–Њ –Є —В–Њ –≤—Б–Є—З–Ї–Њ.
–Ъ–∞–Ј–≤–∞—В, —З–µ –µ–і–љ–∞ –њ—А–Њ–≥—А–∞–Љ–∞ –љ–Є–Ї–Њ–≥–∞ –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б—В–∞–љ–µ –њ–Є—Б–∞—В–µ–ї, –Ї–∞–Ї—В–Њ Photoshop –љ–Є–Ї–Њ–≥–∞ –љ–µ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –†–∞—Д–∞–µ–ї. –Э–Њ –∞–Ї–Њ P = NP, —Й–µ –±—К–і–µ —Б–∞–Љ–Њ –≤—К–њ—А–Њ—Б –љ–∞ –≤—А–µ–Љ–µ, –њ—А–µ–і–Є –љ—П–Ї–Њ–є –і–∞ –Є–Ј–Љ–Є—Б–ї–Є –Ї–∞–Ї –і–∞ —Б–µ —Б—К–Ј–і–∞–і–∞—В –і–Њ–Ї–∞–Ј—Г–µ–Љ–Њ "–≤–µ–ї–Є–Ї–Є" —А–Њ–Љ–∞–љ–Є –Є –Ї–∞—А—В–Є–љ–Є —Б –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞ –µ—Д–µ–Ї—В–Є–≤–љ–Њ—Б—В.
–Т –µ–і–Є–љ —Б–≤—П—В, –≤ –Ї–Њ–є—В–Њ –† –µ –і–Њ–Ї–∞–Ј–∞–љ–Њ —А–∞–≤–љ–Њ –љ–∞ NP, –ї–µ—Б–љ–Њ –Љ–Њ–ґ–µ–Љ –і–∞ –Є–Ј—З–Є—Б–ї–Є–Љ –≤—Б–Є—З–Ї–Њ. –Ф–∞ —Б–Є –њ—А–µ–і—Б—В–∞–≤–Є–Љ, –љ–∞–њ—А–Є–Љ–µ—А, –Њ–љ–Ї–Њ–ї–Њ–≥, –Ї–Њ–Љ—Г—В–Њ –≤–µ—З–µ –љ–µ —Б–µ –љ–∞–ї–∞–≥–∞ –і–∞ —Б–µ –±–Њ—А–Є —Б –њ—А–Њ–±–Є—В–µ –Є –≥—А–µ—И–Ї–Є—В–µ –љ–∞ —Е–Є–Љ–Є–Њ—В–µ—А–∞–њ–Є—П—В–∞, –Ј–∞—Й–Њ—В–Њ "—Б–µ–≥–∞ —Й–µ –Љ–Њ–ґ–µ–Љ –і–∞ —А–∞–Ј–≥–ї–µ–і–∞–Љ–µ –Ф–Э–Ъ –љ–∞ —З–Њ–≤–µ–Ї–∞, –Ї–∞–Ї—В–Њ –Є –љ–∞ –Љ—Г—В–Є—А–∞–ї–Є—П –Ф–Э–Ъ –љ–∞ —А–∞–Ї–Њ–≤–Є—В–µ –Ї–ї–µ—В–Ї–Є, –Є –і–∞ —А–∞–Ј—А–∞–±–Њ—В–Є–Љ –њ—А–Њ—В–µ–Є–љ–Є, –Ї–Њ–Є—В–Њ —Б–µ –Њ–≥—К–≤–∞—В —Б–∞–Љ–Њ –њ–Њ –њ—А–∞–≤–Є–ї–љ–Є—П –љ–∞—З–Є–љ, –µ—Д–µ–Ї—В–Є–≤–љ–Њ –Є–Ј—В–Њ—Й–∞–≤–∞–є–Ї–Є –Њ—В –≥–ї–∞–і —А–∞–Ї–Њ–≤–Є—В–µ –Ї–ї–µ—В–Ї–Є, –±–µ–Ј –і–∞ –њ—А–Є—З–Є–љ—П–≤–∞—В –љ–Є–Ї–∞–Ї–≤–Є –њ—А–Њ–±–ї–µ–Љ–Є –Ј–∞ –љ–Њ—А–Љ–∞–ї–љ–Є—В–µ –Ї–ї–µ—В–Ї–Є", –Ї–∞–Ї—В–Њ –Њ–±—П—Б–љ—П–≤–∞ –Ы–∞–љ—Б –§–Њ—А—В–љ–∞—Г (Lance Fortnow) –≤ –Ї–љ–Є–≥–∞—В–∞ —Б–Є "–Ч–ї–∞—В–љ–Є—П—В –±–Є–ї–µ—В: P, NP –Є –Ґ—К—А—Б–µ–љ–µ—В–Њ –љ–∞ –љ–µ–≤—К–Ј–Љ–Њ–ґ–љ–Њ—В–Њ" (вАЬThe Golden Ticket: P, NP and the Search for the ImpossibleвАЭ).¬†
–°–њ–Њ—А–µ–і¬†–§–Њ—А—В–љ–∞—Г –Њ—В–љ–Њ—И–µ–љ–Є–µ—В–Њ –Љ–µ–ґ–і—Г P –Є NP –µ "–µ–і–Є–љ –Њ—В –љ–∞–є-–≥–Њ–ї–µ–Љ–Є—В–µ –Њ—В–≤–Њ—А–µ–љ–Є –њ—А–Њ–±–ї–µ–Љ–Є –Ј–∞ —Ж—П–ї–∞—В–∞ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞", –љ–µ —Б–∞–Љ–Њ –Ј–∞—Й–Њ—В–Њ –µ –Є–Ј–Ї–ї—О—З–Є—В–µ–ї–љ–Њ —В—А—Г–і–љ–Њ –і–∞ —Б–µ —А–µ—И–Є, –∞ –Ј–∞—Й–Њ—В–Њ –Є–Љ–∞ —В–∞–Ї–Є–≤–∞ –≤—Б–µ–Њ–±—Е–≤–∞—В–љ–Є –њ—А–∞–Ї—В–Є—З–µ—Б–Ї–Є –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П. –Ґ–Њ–≤–∞ –µ –Љ–µ—З—В–∞—В–∞ –Ј–∞ –њ—К–ї–љ–∞ –ї–µ–Ї–Њ—В–∞, –Ј–∞ —Г–≤–µ—А–µ–љ–Њ—Б—В, —З–µ –Є–Љ–∞ –µ—Д–µ–Ї—В–Є–≤–µ–љ –љ–∞—З–Є–љ –і–∞ —Б–µ –Є–Ј—З–Є—Б–ї–Є –њ–Њ—З—В–Є –≤—Б–Є—З–Ї–Њ, "–Њ—В –ї–µ–Ї—Г–≤–∞–љ–µ—В–Њ –љ–∞ —Б–Љ—К—А—В–Њ–љ–Њ—Б–љ–Є –±–Њ–ї–µ—Б—В–Є –і–Њ –њ—А–Є—А–Њ–і–∞—В–∞ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞", –і–Њ—А–Є "–∞–ї–≥–Њ—А–Є—В–Љ–Є—З–µ–љ –њ—А–Њ—Ж–µ—Б –Ј–∞ —А–∞–Ј–њ–Њ–Ј–љ–∞–≤–∞–љ–µ –љ–∞ –≤–µ–ї–Є—З–Є–µ—В–Њ", –њ–Є—И–µ New Yorker.¬†

–Ґ–µ–Њ—А–Є—П—В–∞ –љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ —Б–ї–Њ–ґ–љ–Њ—Б—В
–Ь–љ–Њ–≥–Њ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є, –Љ–∞–Ї–∞—А –Є –љ–µ –≤—Б–Є—З–Ї–Є, —Б–∞ —Б–Ї–ї–Њ–љ–љ–Є –і–∞ —Б–Љ—П—В–∞—В, —З–µ –Њ—В–≥–Њ–≤–Њ—А—К—В –љ–∞ –≤—К–њ—А–Њ—Б–∞ –µ –Њ—В—А–Є—Ж–∞—В–µ–ї–µ–љ, —В.–µ. —З–µ P –≤—Б—К—Й–љ–Њ—Б—В –љ–µ –µ —А–∞–≤–љ–Њ –љ–∞ NP. –Р–Ї–Њ —В–Њ–≤–∞ –µ —В–∞–Ї–∞, —Й–µ –µ –Љ–љ–Њ–≥–Њ —В—А—Г–і–љ–Њ –і–∞ —Б–µ –і–Њ–Ї–∞–ґ–µ —В–∞–Ї–Њ–≤–∞ —В–≤—К—А–і–µ–љ–Є–µ, –Ј–∞—Й–Њ—В–Њ —В—А—П–±–≤–∞ –і–∞ –∞–љ–∞–ї–Є–Ј–Є—А–∞–Љ–µ –≤—Б–Є—З–Ї–Є "–≤—К–Ј–Љ–Њ–ґ–љ–Є" –∞–ї–≥–Њ—А–Є—В–Љ–Є –Є –њ–Њ –љ—П–Ї–∞–Ї—К–≤ –љ–∞—З–Є–љ –і–∞ –і–Њ–Ї–∞–ґ–µ–Љ, —З–µ –љ–Є–Ї–Њ–є –Њ—В —В—П—Е –љ–µ —Б—В–∞–≤–∞. –Ґ–Њ–≤–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ –Љ–љ–Њ–≥–Њ –њ–Њ-—В—А—Г–і–љ–Њ –Њ—В –њ—А–µ–і—Б—В–∞–≤–∞—В–∞ –Ј–∞ –µ–і–Є–љ, –і–Њ—А–Є –Є "—Б–ї–Њ–ґ–µ–љ" –∞–ї–≥–Њ—А–Є—В—К–Љ, –Ї–Њ–є—В–Њ —А–µ—И–∞–≤–∞ –Ї–Њ–љ–Ї—А–µ—В–µ–љ –њ—А–Њ–±–ї–µ–Љ.
–Ъ–∞—В–Њ —Б–µ –Є–Љ–∞ –њ—А–µ–і–≤–Є–і, —З–µ P –≤–µ—А–Њ—П—В–љ–Њ –љ–µ –µ —А–∞–≤–љ–Њ –љ–∞ NP, –≤–µ—А–Њ—П—В–љ–Њ –љ–Є–Ї–Њ–≥–∞ –љ—П–Љ–∞ –і–∞ –±—К–і–∞—В –љ–∞–Љ–µ—А–µ–љ–Є –µ—Д–µ–Ї—В–Є–≤–љ–Є —А–µ—И–µ–љ–Є—П –љ–∞ –њ—А–Њ–±–ї–µ–Љ–Є—В–µ NP - —В–Њ–≥–∞–≤–∞ –Ј–∞—Й–Њ –µ —Ж–µ–ї–Є—П—В —В–Њ–Ј–Є —И—Г–Љ?
–Ь–∞–є–Ї—К–ї –°–Є–њ—Б—К—А (Michael Sipser), —А—К–Ї–Њ–≤–Њ–і–Є—В–µ–ї –љ–∞ –Ї–∞—В–µ–і—А–∞—В–∞ –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –≤ –Ь–∞—Б–∞—З—Г–Ј–µ—В—Б–Ї–Є—П —В–µ—Е–љ–Њ–ї–Њ–≥–Є—З–µ–љ –Є–љ—Б—В–Є—В—Г—В (MIT),¬†–Ї–∞–Ј–≤–∞, —З–µ –њ—А–Њ–±–ї–µ–Љ—К—В —Б P –Є NP –µ –≤–∞–ґ–µ–љ –Ј–∞ –Ј–∞–і—К–ї–±–Њ—З–∞–≤–∞–љ–µ –љ–∞ –љ–∞—И–µ—В–Њ —А–∞–Ј–±–Є—А–∞–љ–µ –Ј–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–∞–љ–∞—В–∞ —Б–ї–Њ–ґ–љ–Њ—Б—В (computational complexity).
–Ґ–µ–Њ—А–Є—П—В–∞ –љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ —Б–ї–Њ–ґ–љ–Њ—Б—В –Є–Ј—Г—З–∞–≤–∞ –њ—А–Њ–±–ї–µ–Љ–Є—В–µ. –Я–Њ-–Ї–Њ–љ–Ї—А–µ—В–љ–Њ —В—П —Б–µ –Њ–њ–Є—В–≤–∞ –і–∞ –Ї–ї–∞—Б–Є—Д–Є—Ж–Є—А–∞ –Ї–Њ–ї–Ї–Њ "—В—А—Г–і–љ–Є" —Б–∞ —В–µ, –і–Њ–Ї–Њ–ї–Ї–Њ –µ—Д–µ–Ї—В–Є–≤–љ–Њ —А–µ—И–µ–љ–Є–µ –љ–∞ –Є–Ј—З–Є—Б–ї–µ–љ–Є–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –љ–∞–Љ–µ—А–Є –њ—А–Є —А–µ–∞–ї–Є—Б—В–Є—З–љ–Є —Г—Б–ї–Њ–≤–Є—П.
–Ґ–Њ–≤–∞ –µ –њ—А–Њ–±–ї–µ–Љ –љ–∞¬†Computer Science¬†("–Ъ–Њ–Љ–њ—О—В—К—А–љ–∞ –љ–∞—Г–Ї–∞").¬†–Э–∞ –∞–љ–≥–ї–Є–є—Б–Ї–Є –µ–Ј–Є–Ї —В–Њ–Ј–Є —В–µ—А–Љ–Є–љ –µ —Б—В–∞–љ–і–∞—А—В–µ–љ, –љ–Њ –љ–∞ –±—К–ї–≥–∞—А—Б–Ї–Є –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–≤–µ–і–µ –±—Г–Ї–≤–∞–ї–љ–Њ. –Ґ–Њ–≤–∞ –µ —В–µ–Њ—А–µ—В–Є—З–љ–∞ –љ–∞—Г–Ї–∞, –∞ –љ–µ –њ—А–Њ–≥—А–∞–Љ–Є—А–∞–љ–µ. –Ґ–Њ–≤–∞ –µ —Б—А–∞–≤–љ–Є—В–µ–ї–љ–Њ –љ–Њ–≤–∞ –Њ–±–ї–∞—Б—В, –Ї–Њ—П—В–Њ –љ—П–Љ–∞ –њ—А—П–Ї–∞ –≤—А—К–Ј–Ї–∞ —Б —З–Є—Б–ї–µ–љ–Є –Љ–µ—В–Њ–і–Є –Є –і—А—Г–≥–Є –њ–Њ–і–Њ–±–љ–Є.

–Ф–≤–Є–ґ–µ–љ–Є–µ—В–Њ –µ –≤—Б–Є—З–Ї–Њ, –Ї—А–∞–є–љ–∞—В–∞ —Ж–µ–ї –µ –љ–Є—Й–Њ
–Т –µ–і–љ–Њ –Є–љ—В–µ—А–≤—О –°–Ї–Њ—В –Р–∞—А–Њ–љ—Б—К–љ (Scott Aaronson), –Ї–Њ–Љ–њ—О—В—К—А–µ–љ —Г—З–µ–љ –Њ—В MIT, –њ–Њ–≤—В–∞—А—П –Љ–Є—Б—К–ї—В–∞ –љ–∞ –С–µ—А–љ—Й–∞–є–љ, –Ї–∞—В–Њ —В–≤—К—А–і–Є, —З–µ –µ –≤–∞–ґ–µ–љ –њ—К—В—П—В, –∞ –љ–µ —Ж–µ–ї—В–∞:
–Ф–∞, –њ–Њ—З—В–Є –≤—Б–Є—З–Ї–Є –Њ—В –љ–∞—Б —Б–Љ—П—В–∞—В –≤–µ—З–µ, —З–µ P –љ–µ –µ —А–∞–≤–љ–Њ –љ–∞ NP. –Э–Њ —В–Њ–≤–∞ –µ –µ–і–љ–Њ –Њ—В –Њ–љ–µ–Ј–Є –љ–µ—Й–∞, –Ї–Њ–Є—В–Њ —Б–∞ –њ–Њ—Б–Њ–Ї–∞, –∞ –љ–µ –Ї—А–∞–є–љ–∞—В–∞ —Ж–µ–ї –љ–∞ –њ—К—В—Г–≤–∞–љ–µ—В–Њ. –Ч–∞ –і–∞ —Б–µ –і–Њ–Ї–∞–ґ–µ —В–≤—К—А–і–µ–љ–Є–µ—В–Њ, —Й–µ –±—К–і–µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –Њ–≥—А–Њ–Љ–љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Ј–љ–∞–љ–Є—П¬†–≤¬†–µ–і–љ–Њ –љ–Њ–≤–Њ —А–∞–Ј–±–Є—А–∞–љ–µ –Ј–∞ –Є–Ј—З–Є—Б–ї–µ–љ–Є—П—В–∞. –Ъ–∞–Ї–≤–Њ —Б–µ –Њ–њ–Є—В–≤–∞–Љ–µ –і–∞ –і–Њ–Ї–∞–ґ–µ–Љ? –Ґ–Њ–≤–∞¬†–Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ —Й–µ –±—К–і–µ —А–µ–∞–ї–љ–Њ¬†—А–µ—И–∞–≤–∞–љ–µ—В–Њ –љ–∞ –≤—Б–Є—З–Ї–Є —В–µ–Ј–Є –љ–µ–ї–Є–љ–µ–є–љ–Є –Њ–њ—В–Є–Љ–Є–Ј–∞—Ж–Є–Њ–љ–љ–Є –Ј–∞–і–∞—З–Є –Є–ї–Є —В–µ–Ј–Є –њ—А–Њ–±–ї–µ–Љ–Є –Ј–∞ —В—К—А—Б–µ–љ–µ, –Є–ї–Є –і–Њ–Ї–∞–Ј–∞—В–µ–ї—Б—В–≤–Њ –љ–∞ —В–µ–Њ—А–µ–Љ–∞ –Ј–∞ –љ–∞–Љ–Є—А–∞–љ–µ—В–Њ –љ–∞ –љ–∞–є-–і–Њ–±—А–Є—П –≥—А–∞—Д–Є–Ї –Ј–∞ –∞–≤–Є–Њ–Ї–Њ–Љ–њ–∞–љ–Є–Є—В–µ, –Є–ї–Є –Ї—А–Є–њ—В–Њ–≥—А–∞—Д—Б–Ї–Є –Ї–Њ–і–Њ–≤–µ - –≤—Б–Є—З–Ї–Є —В–µ–Ј–Є –љ–µ—Й–∞, –Ї–Њ–Є—В–Њ —Б–µ–≥–∞ –љ—П–Љ–∞—В –∞–ї–≥–Њ—А–Є—В—К–Љ. –Ґ–Њ–≤–∞ –µ –љ–µ–≤–µ—А–Њ—П—В–љ–Њ —В—А—Г–і–љ–∞ –Ј–∞–і–∞—З–∞. –Ґ–∞–Ї–∞ —З–µ –Љ–Њ–ґ–µ–Љ –і–∞ –Њ—З–∞–Ї–≤–∞–Љ–µ, —З–µ –њ–Њ –њ—К—В—П –Ї—К–Љ –і–Њ–Ї–∞–Ј–≤–∞–љ–µ—В–Њ –љ–∞ —В–Њ–≤–∞ –љ–µ—Й–Њ —Й–µ –љ–∞—Г—З–Є–Љ –Њ–≥—А–Њ–Љ–љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –µ—Д–µ–Ї—В–Є–≤–љ–Є –∞–ї–≥–Њ—А–Є—В–Љ–Є, –Ї–Њ–Є—В–Њ —Б–∞ –Є–Ј–≤—К–љ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –≤–µ—З–µ –Ј–љ–∞–µ–Љ, –Є –Љ–љ–Њ–≥–Њ, –Љ–љ–Њ–≥–Њ –µ –≤–µ—А–Њ—П—В–љ–Њ —Й–µ –Њ—В–Ї—А–Є–µ–Љ –љ–Њ–≤–Є –∞–ї–≥–Њ—А–Є—В–Љ–Є, –Ї–Њ–Є—В–Њ –≤–µ—А–Њ—П—В–љ–Њ —Й–µ –Є–Љ–∞—В –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П, –Ї–Њ–Є—В–Њ –і–Њ—А–Є –љ–µ –Љ–Њ–ґ–µ–Љ –і–∞ –њ—А–µ–і–≤–Є–і–Є–Љ.
–І–µ—Б—В–Њ –≤ –Є—Б—В–Њ—А–Є—П—В–∞ –љ–∞ —В–µ–Њ—А–µ—В–Є—З–љ–∞—В–∞ –Ї–Њ–Љ–њ—О—В—К—А–љ–∞ –љ–∞—Г–Ї–∞ –Є–і–µ–Є—В–µ, –Ї–Њ–Є—В–Њ –Є–Ј–њ–Њ–ї–Ј–≤–∞–Љ–µ, –Ј–∞ –і–∞ –і–Њ–Ї–∞–ґ–µ–Љ, —З–µ –љ–µ—Й–Њ –µ –љ–µ–≤—К–Ј–Љ–Њ–ґ–љ–Њ, –Љ–Њ–≥–∞—В –і–∞ —Б–µ –Њ–±—К—А–љ–∞—В, –Ј–∞ –і–∞ –і–Њ–Ї–∞–ґ–∞—В, —З–µ –љ–µ—Й–Њ –і—А—Г–≥–Њ –µ –≤—К–Ј–Љ–Њ–ґ–љ–Њ –Є –Њ–±—А–∞—В–љ–Њ—В–Њ.¬†
–Р –µ—В–Њ –µ–і–Є–љ –љ–∞—З–Є–љ, –њ–Њ –Ї–Њ–є—В–Њ –±–Є—Е—В–µ –Љ–Њ–≥–ї–Є –і–∞ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В–µ P вЙ† NP —Б–ї–µ–і–≤–∞—Й–Є—П—В –њ—К—В, –Ї–Њ–≥–∞—В–Њ –њ—А–Њ–њ—Г—Б–љ–µ—В–µ –Ї—А–∞–є–љ–Є—П —Б—А–Њ–Ї –љ–∞ —А–∞–±–Њ—В–∞—В–∞ —Б–Є, –Ї–Њ–≥–∞—В–Њ —А–µ—И–µ–љ–Є–µ—В–Њ –љ—П–Ї–∞–Ї —Б–Є —Г—Б–њ—П–≤–∞ –і–∞ –≤–Є —Г–±–µ–≥–љ–µ, –Ї–∞–ґ–µ—В–µ –љ–∞ –Љ–љ–Њ–≥–Њ –Є–љ—Д–Њ—А–Љ–Є—А–∞–љ–Є—П —Б–Є —И–µ—Д: "–Ч–љ–∞–µ—В–µ, —З–µ P вЙ† NP", –∞ —В–Њ–є —Й–µ –±—К–і–µ –њ—А–Є–љ—Г–і–µ–љ –і–∞ –≤–Є –Њ—В–≥–Њ–≤–Њ—А–Є: "–Ф–∞, —В–∞–Ї–∞ –µ".

–Я–Њ–ї–Ј–∞—В–∞ –Њ—В –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞
–Ь–љ–Њ–≥–Њ –Љ–ї–∞–і–Є —Е–Њ—А–∞ –Є –љ—П–Ї–Њ–Є –≤ —Б—К–Ј–љ–∞—В–µ–ї–љ–∞ –≤—К–Ј—А–∞—Б—В —В–≤—К—А–і—П—В, —З–µ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞ –µ –±–µ–Ј–њ–Њ–ї–µ–Ј–љ–∞ –љ–∞—Г–Ї–∞, —З–µ —Б–ї–µ–і –Ї–∞—В–Њ –Ј–∞–≤—К—А—И–Є–Љ —Г—З–Є–ї–Є—Й–µ –Є–ї–Є –Є–љ—Б—В–Є—В—Г—В, —В—П –љ–µ –Љ–Њ–ґ–µ –і–∞ –љ–Є –±—К–і–µ –њ–Њ–ї–µ–Ј–љ–∞ –≤ –ґ–Є–≤–Њ—В–∞.
–Э–Њ –≤—Б—К—Й–љ–Њ—Б—В —В–Њ–≤–∞ –љ–µ –µ —В–∞–Ї–∞ - –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞ –µ —Б—К–Ј–і–∞–і–µ–љ–∞ –Ї–∞—В–Њ –Љ–µ—Е–∞–љ–Є–Ј—К–Љ, —З—А–µ–Ј –Ї–Њ–є—В–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Њ–њ–Є—И–µ –Є –љ–∞–±–ї—О–і–∞–≤–∞ –љ–∞—И–Є—П¬†—Б–≤—П—В. –Ґ—П –µ –љ–∞–≤—Б—П–Ї—К–і–µ - –≤—К–≤ –≤—Б–µ–Ї–Є –і–Њ–Љ, –≤—К–≤ –≤—Б—П–Ї–∞ —В—А–µ–≤–Є—З–Ї–∞ –Є–ї–Є –Њ–±–ї–∞–Ї.
"–Э–µ –Њ–±–≤–Є–љ—П–≤–∞–є—В–µ —Ж–≤–µ—В—П—В–∞, —З–µ —Б–ї–µ–њ–Є—В–µ –љ–µ –Љ–Њ–≥–∞—В –і–∞ –≥–Є –≤–Є–і—П—В", –Ї–∞–Ј–≤–∞ —А—Г—Б–Ї–Є—П—В –Є—Б—В–Њ—А–Є–Ї –Т–∞—Б–Є–ї–Є–є¬†–Ъ–ї—О—З–µ–≤—Б–Ї–Є–є.
–Ш –∞–Ї–Њ —В–∞–Ј–Є –љ–∞—Г–Ї–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ —Б–ї–Њ–ґ–љ–∞, —В–Њ –Є –љ–∞—И–Є—П—В —Б–≤—П—В –љ–µ –µ —В–Њ–ї–Ї–Њ–≤–∞ –њ—А–Њ—Б—В, –Ї–Њ–ї–Ї–Њ—В–Њ –Є–Ј–≥–ї–µ–ґ–і–∞, –Є –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞ –Љ—Г —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞, –Ј–∞ –і–∞ –Њ—Б–Є–≥—Г—А–Є –Њ—Б–љ–Њ–≤–∞ –Ј–∞ –њ–Њ-–і–Њ–±—А–Њ —А–∞–Ј–±–Є—А–∞–љ–µ —А–µ–∞–ї–љ–Њ—Б—В—В–∞.
–Ш–Ј—В–Њ—З–љ–Є—Ж–Є:
A New Map Traces the Limits of Computation, Quanta magazine
Explained: P vs. NP, MIT News
3 questions: P vs. NP, MIT News
–Э–∞–Ї–Њ–љ–µ—Ж-—В–Њ! P?=NP –Є –Є–љ—Б—В–Є—В—Г—В –Ъ–ї—Н—П
P vs NP Problem, Clay Mathematics Institute
–Ю—Й–µ –њ–Њ —В–µ–Љ–∞—В–∞

–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–С—К–ї–≥–∞—А–Є–љ—К—В –Ф–Њ–±—А–Є –С–Њ–ґ–Є–ї–Њ–≤ –њ—А–µ–і–ї–∞–≥–∞ —А–µ—И–µ–љ–Є–µ –љ–∞ –Ј–∞–і–∞—З–∞, –Ї–Њ—П—В–Њ –љ–µ –µ —А–µ—И–µ–љ–∞ 40 –≥.
–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–•–Є–њ–Њ—В–µ–Ј–∞—В–∞ –љ–∞ –†–Є–Љ–∞–љ –Ј–∞ –ї–∞–Є—Ж–Є

–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Э–Є–≥–µ—А–Є–є—Б–Ї–Є –Љ–∞—В–µ–Љ–∞—В–Є–Ї –µ –Ј–∞—П–≤–Є–ї, —З–µ –µ –љ–∞–Љ–µ—А–Є–ї —А–µ—И–µ–љ–Є–µ—В–Њ –љ–∞ –Ј–∞–і–∞—З–∞ –Ј–∞ 1 –Љ–ї–љ –і–Њ–ї–∞—А–∞

















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
21919
1
20.09 2017 –≤ 11:30
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
dolivo
–Ч–µ–Љ—П—В–∞ –њ–Њ—В—К–Љ–љ—П–≤–∞. –Ъ–∞–Ї–≤–Њ –Њ–Ј–љ–∞—З–∞–≤–∞ —В–∞–Ј–Є —В—А–µ–≤–Њ–ґ–љ–∞ –Ї–ї–Є–Љ–∞—В–Є—З–љ–∞ —В–µ–љ–і–µ–љ—Ж–Є—П –Ј–∞ –±—К–і–µ—Й–µ—В–Њ?
Nikor
–Э–∞ 30 —Б–µ–њ—В–µ–Љ–≤—А–Є 1928 –µ –Њ—В–Ї—А–Є—В –њ–µ–љ–Є—Ж–Є–ї–Є–љ—К—В
–Я—А–Њ—Б—В –І–Њ–≤–µ–Ї
–Э–Њ–≤–Њ –Њ–±—П—Б–љ–µ–љ–Є–µ –Ј–∞ –≥–Є–≥–∞–љ—В—Б–Ї–Є—В–µ –µ–Ї—Б–њ–ї–Њ–і–Є—А–∞—Й–Є –Ї—А–∞—В–µ—А–Є –≤ –°–Є–±–Є—А
dolivo
–Ъ–ї–Є–Љ–∞—В–Є—З–љ–Є—П—В —Б–Ї–µ–њ—В–Є—Ж–Є–Ј—К–Љ вАУ –љ–∞–є-—Б–Ї—К–њ–∞—В–∞ –ї—К–ґ–∞ –љ–∞ –љ–∞—И–µ—В–Њ –≤—А–µ–Љ–µ
helper68
–Ш–Ј–њ–Њ–ї–Ј–≤–∞–љ–µ—В–Њ –љ–∞ —Б–Љ–∞—А—В—Д–Њ–љ –≤ —В–Њ–∞–ї–µ—В–љ–∞—В–∞ –µ —Б–≤—К—А–Ј–∞–љ–Њ —Б 46% –њ–Њ-–≤–Є—Б–Њ–Ї —А–Є—Б–Ї –Њ—В —Е–µ–Љ–Њ—А–Њ–Є–і–Є