
Днес се отбелязва Световния ден на числото "пи".
Денят, в който се чества най-старата математическата константа, е 14 март или 3.14 по американския модел на календарен запис месец/ден.
Може да се каже, че това е празник на математиката и най-често се празнува с печене на голям брой пайове.
Но "пи" не е само парче пай
Пи (π) е едно от най-важните и интересни числа в математиката. Съотношението на дължината на окръжността към нейния диаметър е еднакво за всички окръжности. Това съотношение се означава с гръцката буква π, която е първата буква от гръцката дума περιμετροη, която означава "окръжност").
Историята на неговото изчисляване започва преди повече от 2 хиляди години, а точността на изчисление варира от 256/81 до 339/108 в древен Египет и в индийските свещени книги Ведите.
- Архимед изчислява съотношението на дължината на окръжността към диаметъра на дължина или числото π и установява, че е между 3 10/71 и 3 1/7.
- Дълго време като приблизителна стойност се е използвала 22/7, макар че е открито в Китай още през V век едно по-добро приближение 355/113 = 3.1415929 , което е преоткрито в Европа едва през XVI век.
- През 1579 г. френският математик Франсоа Виет изчислява "пи" до 9 знака.
- Холандският математик Лудолф Ван Цейлен през 1596 г. публикува резултата на своя десетилетен труд – числото "пи", изчислено с 32 знака. И затова преди години числото "пи" е наричано "лудолфово число".
Но всички тези изчисления са правени по методите, посочени от Архимед - кръга се заменя с многоъгълник с нарастващ брой страни. Периметърът на вписания многоъгълник по този начин е по-малък от обиколката на кръга, а периметъра на описания многоъгълник - по-голям.
 |
Но остава неясно дали числото π е рационално, тоест, дали може да се изрази като отношение на две цели числа, или е ирационално.
Едва през 1767 г. немският математик Ламберт доказва, че числото π е ирационално.
А след още сто години през 1882 г. друг немски математик, Ф. Линдеман, доказва неговата трансцендентност, което означава, че е невъзможно да се построи с помощта на пергел и линийка квадрат с равна площ на дадена окръжност.

Случайни ли са цифрите на "пи"?
Още от зората на математиката хората се питат дали цифрите на числото π (= 3.1415926535 ...) са "случайни" - от Архимед до компютърната ера в наши дни. Сегашният рекорд от 10 трилиона цифри след десетичната точка се държи от Александър Йе (Alexander Yee) и Шигуро Кондо (Shiguro Kondo). Преди време бе разпространен един мем за π, който твърди, наред с други неща:
"Пи" е безкрайно неповтарящо се десетично число, което означава, че всяка възможна комбинация на числа съществува някъде в π. Превърнато в ASCII текст, някъде в тази безкрайна поредица от цифри е името на всеки човек, който някога сте обичали, датата, часа и начина на смъртта ви и отговорите на всички големи въпроси на Вселената.
Дали това наистина е вярно? Дали цифрите на π наистина са "случайни"? Дали всяка възможна поредица от цифри в крайна сметка се появява някъде в безкрайната десетична редица на π? Отговорът бе неясен.
След като векове математиците си блъскат главите над този проблем, може би, най-накрая има напредък. Първият голям пробив става през 1996 г., когато Дейвид Бейли (David Bailey), Питър Борвайн (Peter Borwein) и Саймън Плуф (Simon Plouffe) откриват тази невероятна нова формула:
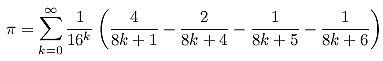 |
Това е вълнуващо не само защото формулата е нова, но и защото тя дава възможност за лесно изчисление на всяка изолирана шестнадесетична или двоична цифра на π , без да е необходимо да се изчисли всяка от предходните цифри. Постигнато е това, което по-рано се смяташе за невъзможно. (За информация как работи формулата, поместваме готов код на езика на C, изчисляваща 1000000-ия знак в края на статията.)
И макар резултатът да не позволява изчисление в по-познатите ни десетични цифри, формулата изглежда добавя още доказателства, че цифрите на π са случайни. "Ако може да се получат лесно цифрите по този начин, то тогава това е силно доказателство, че цифрите са независими", заяви Борвайн.
Това доказва, че всяка последователност от цифри има равен шанс да се появи в цифрите на π в една и съща дължина последователности. Това е т. нар. свойство нормалност.
"В познатата десетична бройна система на основа 10, всяка една цифра на нормално число се появява в една десета от случаите, а всяко двуцифрена комбинация възниква на всеки един случай на сто и така нататък", обяснява Бейли. "Това е като безкрайно хвърляне на честен десестенен зар и да се преброи колко често се появява всяка страна или комбинация от страни". "Пи" със сигурност изглежда се държи по този начин, поне за първите 10 млрд. десетични цифри. Досега известните цифри от π преминаха всеки статистически тест за нормалност, а което значи и на случайността.
 Първите 1000 знака на "пи". Източник: Wikiwand
Първите 1000 знака на "пи". Източник: Wikiwand
Тук трябва да си изясним какво се има предвид под "случайни". Ясно е, че "пи" не е "случайно" число в тесния смисъл на думата, защото отделните цифри със сигурност не случайни, а математически определени точно. Под "случайност" се разбира математическия термин "нормалност".
Намесва се Хаосът
Въпреки това, нормалността е изключително трудно да се докаже. Всъщност, въпреки че математиците смятат, че повечето математически константи са нормални - π, log2, √2 те досега не го доказаха за нито една от тях. Вместо това, Бейли и Ричард Крандел (Richard Crandell), неочаквано успяха да свържат нормалността с привидно несвързаната област на хаотичните динамични системи. "Аз не съм наясно каква е връзката между теорията на хаоса и теорията на числата", заяви Бейли. "Едното поле възниква от изчислителната физика, а другото е най-чистата от чистата математика".
През последните години за решаване на проблема са впрегнати някои сложни нови инструменти и вече се появиха обещаващи резултати. Така например в книгата "Разходки с реални числа" (Walking on real numbers) на Борвайн и Франциско Арагон Артачо (Francisco J. Aragon Artacho) се анализират цифрите на математическите константи се представят като случайна разходка. Например, един число, изразено на основа 4 ( т.е. използват се цифрите 0, 1, 2 и 3) може да се визуализира, като се започне от дадена точка, движейки се в полето с една единица ход надясно за 0, една единица нагоре за 1, наляво с една единица за 2 или надолу с една единица за 3, като това продължава за толкова цифри, колкото може да се изчисли.
Когато пи в 4-ната система се нанесе по това правило, се получава тази поразително красива картина:

Тази разпечатка е напълно аналогична на тази от поредица цифри, генерирани от генератор на псевдослучайни числа:

Псевдослучайният генератор на числа използване на изчислителни алгоритми, които връщат като резултат дълги поредици от очевидно случайни числа, които всъщност са напълно определени от друга по-кратка начална стойност или ключ. По този начин една и съща последователност от числа може да бъде възпроизвеждана неограничен брой път, ако се знае началната стойност, която определя алгоритъма.
Точно същият случай имаме при изчисляването на числото "пи".
Така че, с други думи, от тези резултати излиза, че хипотезата, че "пи" е определено "нормално" е правдоподобна.
Но нямаме доказателства. Дали този проблем завинаги ще остане, въпреки яростната атака на световната армия компютърно грамотни математици?
Дотогава ще им се наложи да изядат още много пай.
 Eric Sonstroem/Flickr (CC BY 2.0)
Eric Sonstroem/Flickr (CC BY 2.0)
Източници:
Вычисление N-го знака числа Пи без вычисления предыдущих

























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
8010
1
21.10 2019 в 11:21
Последни коментари
Прост Човек
Ново обяснение за гигантските експлодиращи кратери в Сибир
dolivo
Климатичният скептицизъм – най-скъпата лъжа на нашето време
helper68
Използването на смартфон в тоалетната е свързано с 46% по-висок риск от хемороиди
YKoshev
Доколко съвместими са минерално-суровинният отрасъл и чистата околна среда?
Козон
Мистериозен череп на гръцки хоминин е датиран на поне 286 000 години