

–ü—Ä–ł—Ä–ĺ–ī–į —Ā—Ä–Ķ—Č—É –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—ā–į –Ĺ–į –ē–≤–ļ–Ľ–ł–ī
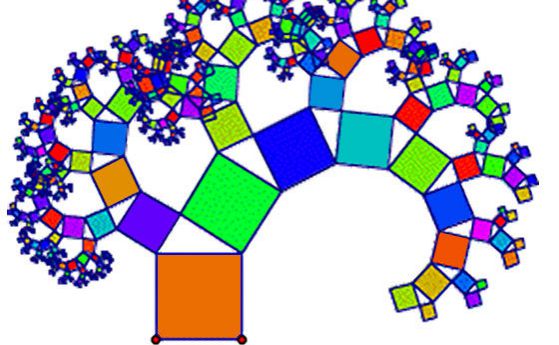
–ú–Ĺ–ĺ–∑–ł–Ĺ–į –Ĺ–Ķ —Ö–į—Ä–Ķ—Ā–≤–į—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į. –Ě–į–ľ–ł—Ä–į—ā —Ź –∑–į —ā–≤—ä—Ä–ī–Ķ –ĺ—ā–≤–Ľ–Ķ—á–Ķ–Ĺ–į –ł –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–į, –ī–ĺ—Ä–ł –ł –Ĺ–į–Ļ-–Ĺ–į–≥–Ľ–Ķ–ī–Ĺ–į—ā–į –Ļ —á–į—Ā—ā - –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź—ā–į. –Ě–ł–ľ–į —Ą–ĺ—Ä–ľ–į—ā–į –Ĺ–į –Ņ–Ľ–į–Ĺ–ł–Ĺ–ł—ā–Ķ, –ī—ä—Ä–≤–Ķ—ā–į—ā–į, –ĺ–Ī–Ľ–į—Ü–ł—ā–Ķ –ł–Ľ–ł –ľ–ĺ—Ä–Ķ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ĺ–Ņ–ł—ą–Ķ —Ā –Ņ–į—Ä–į–Ľ–Ķ–Ľ–Ķ–Ņ–ł–Ņ–Ķ–ī–ł, –Ņ–ł—Ä–į–ľ–ł–ī–ł, —Ā—Ą–Ķ—Ä–ł¬†–ł –Ņ—Ä–ł–∑–ľ–ł? –Ě–ł–ľ–į –ľ–ĺ–∂–Ķ–ľ –≤ —ā–Ķ–∑–ł –ł–∑—á–ł—Ā—ā–Ķ–Ĺ–ł, –≥–Ľ–į–ī–ļ–ł, –Ņ—Ä–ĺ—Ā—ā–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł —Ą–ĺ—Ä–ľ–ł –ī–į –≤–ľ–Ķ—Ā—ā–ł–ľ —Ü—Ź–Ľ–į—ā–į –ļ—Ä–į—Ā–ĺ—ā–į –Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į?
–ě—ā —Ā—ā–≤–ĺ–Ľ–į –Ĺ–į –ī—ä—Ä–≤–ĺ—ā–ĺ —Ā–Ķ —Ä–į–∑–Ņ–Ķ—Ä–≤–į—ā –ī–Ķ–Ī–Ķ–Ľ–ł –ļ–Ľ–ĺ–Ĺ–ł, –ĺ—ā —ā—Ź—Ö - –Ņ–ĺ-–ľ–į–Ľ–ļ–ł –ļ–Ľ–ĺ–Ĺ—á–Ķ—ā–į, –ī–ĺ–ļ–į—ā–ĺ —Ā—ā–ł–≥–Ĺ–Ķ–ľ –ī–ĺ –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ł—ā–Ķ –≤–Ķ–Ļ–ļ–ł. –ö—Ä—ä–≤–ĺ–Ĺ–ĺ—Ā–Ĺ–į—ā–į –Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–į –Ķ —É—Ā—ā—Ä–ĺ–Ķ–Ĺ–į –Ņ–ĺ —Ā—ä—Č–ł—Ź –Ĺ–į—á–ł–Ŭ†-¬†–į—Ä—ā–Ķ—Ä–ł–ł—ā–Ķ —Ā–Ķ —Ä–į–∑–ļ–Ľ–ĺ–Ĺ—Ź–≤–į—ā –≤ –Ņ–ĺ-–ľ–į–Ľ–ļ–ł —Ā—ä–ī–ĺ–≤–Ķ –ł —ā–į–ļ–į –ī–ĺ –Ĺ–į–Ļ-–ľ–į–Ľ–ļ–ł—ā–Ķ –ļ–į–Ņ–ł–Ľ—Ź—Ä–ł.
–ź–ļ–ĺ —Ā–Ķ –≤–≥–Ľ–Ķ–ī–į—ā–Ķ –≤ –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł –ĺ–Ī–Ķ–ļ—ā–ł –ļ–į—ā–ĺ —Ü—Ź–Ľ–ĺ, –į —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į –≤ –Ķ–ī–Ĺ–į —á–į—Ā—ā –ĺ—ā —ā—Ź—Ö, —É–≤–Ķ–Ľ–ł—á–į–≤–į–Ļ–ļ–ł –ľ–į—Č–į–Ī–į, –į —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į –≤ —á–į—Ā—ā –ĺ—ā —ā–į–∑–ł —á–į—Ā—ā –ł —ā. –Ĺ., —Č–Ķ —É—Ā—ā–į–Ĺ–ĺ–≤–ł—ā–Ķ, —á–Ķ —ā–Ķ –ł–∑–≥–Ľ–Ķ–∂–ī–į—ā –Ņ–ĺ—á—ā–ł –Ķ–ī–Ĺ–į–ļ–≤–ĺ.
–Ę–ĺ–≤–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ –Ĺ–į –ĺ–Ī–Ķ–ļ—ā–ł—ā–Ķ —Ā–Ķ –Ĺ–į—Ä–ł—á–į —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ĺ—Ā—ā, –į —Ā–į–ľ–ł—ā–Ķ –ĺ–Ī–Ķ–ļ—ā–ł - —Ą—Ä–į–ļ—ā–į–Ľ–ł.

–ö–ĺ–Ļ –Ķ –ł–∑–ľ–ł—Ā–Ľ–ł–Ľ —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ?
–ú–į–ļ–į—Ä —á–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ—ā–ĺ "—Ą—Ä–į–ļ—ā–į–Ľ" –ī–į —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į —Ā—Ä–į–≤–Ĺ–ł—ā–Ķ–Ľ–Ĺ–ĺ –ĺ—ā—Ā–ļ–ĺ—Ä–ĺ, –Ņ—ä—Ä–≤–ł—ā–Ķ –ł–ī–Ķ–ł –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–į—ā–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź, —Ā–į –≤—ä–∑–Ĺ–ł–ļ–Ĺ–į–Ľ–ł –ĺ—Č–Ķ –Ņ—Ä–Ķ–∑ 19 –≤–Ķ–ļ.
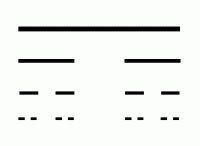 –ü—Ä–Ķ–∑ 1883–≥. –ď–Ķ–ĺ—Ä–≥ –ö–į–Ĺ—ā–ĺ—Ä, –Ķ–ī–ł–Ĺ –ĺ—ā –ĺ—Ā–Ĺ–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ –Ĺ–į —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į—ā–į, –ĺ–Ņ–ł—Ā–≤–į –ļ–į–ļ —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–į, –Ņ–ĺ–≤—ā–į—Ä—Ź—Č–į —Ā–Ķ –Ņ—Ä–ĺ—Ü–Ķ–ī—É—Ä–į, –Ņ—Ä–Ķ–≤—Ä—ä—Č–į –Ľ–ł–Ĺ–ł—Ź –≤ –Ĺ–Ķ—Ā–≤—ä—Ä–∑–į–Ĺ–ł —ā–ĺ—á–ļ–ł - —Ą—Ä–į–ļ—ā–į–Ľ, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ –Ņ—Ä–į—Ö –Ĺ–į –ö–į–Ĺ—ā–ĺ—Ä –ł–Ľ–ł –≥—Ä–Ķ–Ī–Ķ–Ĺ –Ĺ–į¬†–ö–į–Ĺ—ā–ĺ—Ä. –ě–Ī—Ä–į–∑—É–≤–į —Ā–Ķ –ļ–į—ā–ĺ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ —Ā–Ķ –Ņ—Ä–Ķ–ľ–į—Ö–≤–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ —Ā—Ä–Ķ–ī–Ĺ–į—ā–į —ā—Ä–Ķ—ā–ł–Ĺ–į –Ĺ–į –Ķ–ī–Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į. –ü–ĺ–≤—ā–ĺ—Ä–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —ā–į–∑–ł –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź –ī–ĺ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā –≤–ĺ–ī–ł –ī–ĺ –ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā.–Ĺ. –ļ–į–Ĺ—ā–ĺ—Ä–ĺ–≤–ł –Ņ—Ä–į—ą–ł–Ĺ–ļ–ł, —Ā—É–ľ–į—ā–į –ĺ—ā –ī—ä–Ľ–∂–ł–Ĺ–ł—ā–Ķ –Ĺ–į –ļ–ĺ–ł—ā–ĺ –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į 0.
–ü—Ä–Ķ–∑ 1883–≥. –ď–Ķ–ĺ—Ä–≥ –ö–į–Ĺ—ā–ĺ—Ä, –Ķ–ī–ł–Ĺ –ĺ—ā –ĺ—Ā–Ĺ–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ –Ĺ–į —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į—ā–į, –ĺ–Ņ–ł—Ā–≤–į –ļ–į–ļ —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–į, –Ņ–ĺ–≤—ā–į—Ä—Ź—Č–į —Ā–Ķ –Ņ—Ä–ĺ—Ü–Ķ–ī—É—Ä–į, –Ņ—Ä–Ķ–≤—Ä—ä—Č–į –Ľ–ł–Ĺ–ł—Ź –≤ –Ĺ–Ķ—Ā–≤—ä—Ä–∑–į–Ĺ–ł —ā–ĺ—á–ļ–ł - —Ą—Ä–į–ļ—ā–į–Ľ, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ –Ņ—Ä–į—Ö –Ĺ–į –ö–į–Ĺ—ā–ĺ—Ä –ł–Ľ–ł –≥—Ä–Ķ–Ī–Ķ–Ĺ –Ĺ–į¬†–ö–į–Ĺ—ā–ĺ—Ä. –ě–Ī—Ä–į–∑—É–≤–į —Ā–Ķ –ļ–į—ā–ĺ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ —Ā–Ķ –Ņ—Ä–Ķ–ľ–į—Ö–≤–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ —Ā—Ä–Ķ–ī–Ĺ–į—ā–į —ā—Ä–Ķ—ā–ł–Ĺ–į –Ĺ–į –Ķ–ī–Ĺ–į –ĺ—ā—Ā–Ķ—á–ļ–į. –ü–ĺ–≤—ā–ĺ—Ä–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —ā–į–∑–ł –ĺ–Ņ–Ķ—Ä–į—Ü–ł—Ź –ī–ĺ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā –≤–ĺ–ī–ł –ī–ĺ –ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā.–Ĺ. –ļ–į–Ĺ—ā–ĺ—Ä–ĺ–≤–ł –Ņ—Ä–į—ą–ł–Ĺ–ļ–ł, —Ā—É–ľ–į—ā–į –ĺ—ā –ī—ä–Ľ–∂–ł–Ĺ–ł—ā–Ķ –Ĺ–į –ļ–ĺ–ł—ā–ĺ –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į 0.
 |
|||
| 1 | 2 | 3 | 4 |
–ú–ĺ–∂–Ķ –ī–į —Ā–Ķ –ļ–į–∂–Ķ, —á–Ķ –Ņ—ä—Ä–≤–ł—Ź —Ą—Ä–į–ļ—ā–į–Ľ –Ķ –ĺ–Ņ–ł—Ā–į–Ĺ –≤ ‚Äú–ú–ĺ–∑–į–Ļ–ļ–ł, —Ą–ĺ—Ä–ľ–ł—Ä–į–Ĺ–ł –ĺ—ā –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł‚ÄĚ –ĺ—ā ‚Äú–†—ä–ļ–ĺ–≤–ĺ–ī—Ā—ā–≤–ĺ –Ĺ–į –∂–ł–≤–ĺ–Ņ–ł—Ā–Ķ—Ü–į‚ÄĚ (1525–≥) –ĺ—ā –ź–Ľ–Ī—Ä–Ķ—Ö—ā –Ē—é—Ä–Ķ—Ä. –Ę–ĺ–≤–į –Ķ —ā.–Ĺ. –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ –Ĺ–į –ź–Ľ–Ī—Ä–Ķ—Ö—ā –Ē—é—Ä–Ķ—Ä ‚Äď –Ņ–Ķ—ā –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł—Ü–ł —Ā–Ķ –Ņ–ĺ–ī—Ä–Ķ–∂–ī–į—ā –ĺ–ļ–ĺ–Ľ–ĺ –ł–ī–Ķ–Ĺ—ā–ł—á–Ķ–Ĺ –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ. –Ę–į–∑–ł –≥—Ä—É–Ņ–į –ĺ—ā —ą–Ķ—Ā—ā –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ–į –ł–ľ–į —Ą–ĺ—Ä–ľ–į—ā–į –Ĺ–į –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ, –Ĺ–į –ļ–ĺ–Ļ—ā–ĺ —Ā–į –ĺ—ā—Ā—ā—Ä–į–Ĺ–ł –Ņ–Ķ—ā —ā—Ä–ł—ä–≥—ä–Ľ–Ĺ–ł –ļ–Ľ–ł–Ĺ–ĺ–≤–Ķ. –Ę–į–ļ–į, —Ā –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ –ł–∑—Ä—Ź–∑–≤–į–Ĺ–Ķ –Ĺ–į –ļ–Ľ–ł–Ĺ–ĺ–≤–Ķ —Ā–Ķ –ĺ–Ī—Ä–į–∑—É–≤–į –≤—Ā—Ź–ļ–į —Ā–Ľ–Ķ–ī–≤–į—Č–į –ł—ā–Ķ—Ä–į—Ü–ł—Ź.
–ė–∑—É—á–į–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ –≤ –ļ—Ä–į—Ź –Ĺ–į XIX –ł XX –≤–Ķ–ļ –Ķ –Ī–ł–Ľ–ĺ –Ņ–ĺ-—Ā–ļ–ĺ—Ä–ĺ –Ķ–Ņ–ł–∑–ĺ–ī–ł—á–Ĺ–ĺ, –į –Ĺ–Ķ —Ā–ł—Ā—ā–Ķ–ľ–į—ā–ł—á–Ĺ–ĺ –∑–į–Ĺ–ł–ľ–į–Ĺ–ł–Ķ, –∑–į—Č–ĺ—ā–ĺ —ā–ĺ–≥–į–≤–į—ą–Ĺ–ł—ā–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł —Ā–į –Ņ—Ä–Ķ–ī–Ņ–ĺ—á–ł—ā–į–Ľ–ł –ĺ–Ī–Ķ–ļ—ā–ł, –ļ–ĺ–ł—ā–ĺ —Ā–Ķ –ĺ–Ņ–ł—Ā–≤–į—ā —Ā –ļ–Ľ–į—Ā–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –ľ–Ķ—ā–ĺ–ī–ł –ł —ā–Ķ–ĺ—Ä–ł–ł. –Ě–ĺ –ī–ĺ—Ä–ł –ł –ī–į —Ā–Ķ –∑–į—Ö–≤–į–Ĺ–į—ā —Ā —ā–į–∑–ł —ā–Ķ–ľ–į, —ā–Ķ –Ĺ–Ķ —Ā–į –ľ–ĺ–≥–Ľ–ł –ī–į —Ā—ä—Ā—ā–į–≤—Ź—ā –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ĺ–į —ā–ĺ–∑–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ľ–ĺ–ī–Ķ–Ľ, –∑–į—Č–ĺ—ā–ĺ —Ā–į –Ī–ł–Ľ–ł –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł –ĺ–≥—Ä–ĺ–ľ–Ĺ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł—Ź, –ļ–ĺ–ł—ā–ĺ –Ī–ł–Ľ–ĺ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –ī–į —Ā–Ķ –ł–∑–≤—ä—Ä—ą–į—ā —Ä—ä—á–Ĺ–ĺ.

–° –≤—ä–∑—Ö–ĺ–ī–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–į—ā–į —ā–Ķ—Ö–Ĺ–ł–ļ–į —Ā—ā–į–≤–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –ī–į —Ā–Ķ –≤–ł–ī—Ź—ā —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ –≤ —Ü–Ķ–Ľ–ł—Ź—ā –ł–ľ –Ī–Ľ—Ź—Ā—ä–ļ –ł –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ.¬†–ü—ä—Ä–≤–ł—Ź—ā, –ļ–ĺ–Ļ—ā–ĺ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä –∑–į —ā–į–∑–ł —Ü–Ķ–Ľ –Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ—ä—ā –ĺ—ā –ļ–ĺ–ľ–Ņ–į–Ĺ–ł—Ź—ā–į –Ĺ–į IBM –Ď–Ķ–Ĺ–ĺ–į –Ď. –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā (Benoit B. Mandelbrot).
–ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ķ —Ä–ĺ–ī–Ķ–Ĺ –≤—ä–≤ –í–į—Ä—ą–į–≤–į –Ņ—Ä–Ķ–∑ 1924 –≥., –Ĺ–ĺ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–ĺ—ā–ĺ –ľ—É –Ķ–ľ–ł–≥—Ä–ł—Ä–į –≤ –ü–į—Ä–ł–∂, –ļ—ä–ī–Ķ—ā–ĺ 12-–≥–ĺ–ī–ł–Ĺ–ł—ą–Ĺ–ł—Ź—ā –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ņ–ĺ–Ņ–į–ī–į –Ņ–ĺ–ī –≤–Ľ–ł—Ź–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —á–ł—á–ĺ —Ā–ł –®–ĺ–Ľ–Ķ–ľ –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ–Ļ—ā, –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –Ņ–į—Ä–ł–∂–ļ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ. –ú–į–Ľ–ļ–ł—Ź—ā –Ď–Ķ–Ĺ–ĺ–į –Ĺ—Ź–ľ–į–Ľ –ĺ—Ā–ĺ–Ī–Ķ–Ĺ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā –ļ—ä–ľ —É—á–ł–Ľ–ł—Č–Ķ, –Ĺ–ĺ —É –Ĺ–Ķ–≥–ĺ —Ā–Ķ —Ä–į–∑–ļ—Ä–ł–Ľ –Ĺ–Ķ–ĺ–Ī–ł—á–į–Ķ–Ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł —ā–į–Ľ–į–Ĺ—ā, –ļ–ĺ–Ļ—ā–ĺ –ľ—É –ī–į–≤–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā –≤–Ķ–ī–Ĺ–į–≥–į —Ā–Ľ–Ķ–ī –ļ—Ä–į—Ź –Ĺ–į –≤–ĺ–Ļ–Ĺ–į—ā–į, –∑–į –ī–į —Ā—ā–į–Ĺ–Ķ —Ā—ā—É–ī–Ķ–Ĺ—ā –≤ Ecole Polytechnique –≤ –ü–į—Ä–ł–∂. –Ď–Ķ–Ĺ–ĺ–į –Ņ—Ä–ł—ā–Ķ–∂–į–≤–į–Ľ –ĺ—ā–Ľ–ł—á–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ –≤—ä–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ. –Ē–ĺ—Ä–ł –į–Ľ–≥–Ķ–Ī—Ä–ł—á–Ĺ–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–ł —ā–ĺ–Ļ —Ä–Ķ—ą–į–≤–į–Ľ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ. –°–Ľ–Ķ–ī –ī–ł–Ņ–Ľ–ĺ–ľ–ł—Ä–į–Ĺ–Ķ—ā–ĺ —Ā–ł –≤ –Ņ–į—Ä–ł–∂–ļ–ł—Ź —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–Ķ, –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –ĺ—ā–ł–≤–į –≤ –°–ź–©, –ļ—ä–ī–Ķ—ā–ĺ –∑–į–≤—ä—Ä—ą–≤–į –ł –ö–į–Ľ–ł—Ą–ĺ—Ä–Ĺ–ł–Ļ—Ā–ļ–ł—Ź —ā–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł—á–Ķ–Ĺ –ł–Ĺ—Ā—ā–ł—ā—É—ā. –í—Ä—ä—Č–į —Ā–Ķ –≤—ä–≤ –§—Ä–į–Ĺ—Ü–ł—Ź, –ļ—ä–ī–Ķ—ā–ĺ –Ņ–ĺ–Ľ—É—á–į–≤–į –ī–ĺ–ļ—ā–ĺ—Ä—Ā–ļ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ –≤ –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –ü–į—Ä–ł–∂ –Ņ—Ä–Ķ–∑ 1952. –ü—Ä–Ķ–∑ 1955 –≥. —Ā–Ķ –Ņ—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į –≤ –Ė–Ķ–Ĺ–Ķ–≤–į.
–ü—Ä–Ķ–∑ 1958 –≥. –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā —Ā–Ķ —É—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į –≤ –°–ź–©, –ļ—ä–ī–Ķ—ā–ĺ –∑–į–Ņ–ĺ—á–≤–į –ī–į —Ä–į–Ī–ĺ—ā–ł –≤ –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ā–ļ–ł—Ź —Ü–Ķ–Ĺ—ā—ä—Ä –Ĺ–į IBM –≤ –ô–ĺ—Ä–ļ—ā–į—É–Ĺ, –∑–į—Č–ĺ—ā–ĺ –≤ IBM –Ņ–ĺ —ā–ĺ–≤–į –≤—Ä–Ķ–ľ–Ķ —Ā–į —Ā–Ķ –∑–į–Ĺ–ł–ľ–į–≤–į–Ľ–ł —Ā –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ł –∑–į –Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –ĺ–Ī–Ľ–į—Ā—ā–ł –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į.
–ė–∑—Ā–Ľ–Ķ–ī–≤–į–Ļ–ļ–ł –Ĺ–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī —Ā–Ľ—É—á–į–Ļ–Ĺ–ł –ļ–ĺ–Ľ–Ķ–Ī–į–Ĺ–ł—Ź –≤ —Ü–Ķ–Ĺ–ł—ā–Ķ, –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –ĺ—ā–ļ—Ä–ł–Ľ, —á–Ķ —ā–Ķ —Ā–Ľ–Ķ–ī–≤–į—ā —Ā–ļ—Ä–ł—ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł —Ä–Ķ–ī –≤—ä–≤ –≤—Ä–Ķ–ľ–Ķ—ā–ĺ, –ļ–ĺ–Ļ—ā–ĺ –Ĺ–Ķ —Ā–Ķ –ĺ–Ņ–ł—Ā–≤–į —Ā—ä—Ā —Ā—ā–į–Ĺ–ī–į—Ä—ā–Ĺ–ł –ļ—Ä–ł–≤–ł.
–Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ņ—Ä–ĺ—É—á–≤–į–Ľ —Ü–Ķ–Ĺ–ł—ā–Ķ –Ĺ–į –Ņ–į–ľ—É–ļ–į –≤ –Ņ—Ä–ĺ–ī—ä–Ľ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –ī—ä–Ľ—ä–≥ –Ņ–Ķ—Ä–ł–ĺ–ī –ĺ—ā –≤—Ä–Ķ–ľ–Ķ (–Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā —Ā—ā–ĺ –≥–ĺ–ī–ł–Ĺ–ł). –ö–ĺ–Ľ–Ķ–Ī–į–Ĺ–ł—Ź—ā–į –Ĺ–į —Ü–Ķ–Ĺ–ł—ā–Ķ –ł–∑–≥–Ľ–Ķ–∂–ī–į–Ľ–ł –Ņ—Ä–ĺ–ł–∑–≤–ĺ–Ľ–Ĺ–ł, –Ĺ–ĺ –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –ĺ—ā–ļ—Ä–ł–Ľ —Ā–ł–ľ–Ķ—ā—Ä–ł—Ź –ľ–Ķ–∂–ī—É –ī—ä–Ľ–≥–ĺ—Ā—Ä–ĺ—á–Ĺ–ł—ā–Ķ –ł –ļ—Ä–į—ā–ļ–ĺ—Ā—Ä–ĺ—á–Ĺ–ł—ā–Ķ –ļ–ĺ–Ľ–Ķ–Ī–į–Ĺ–ł—Ź –≤ —Ü–Ķ–Ĺ–ł—ā–Ķ. –Ę–į–ļ–į –Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ņ–ĺ–Ľ–į–≥–į –ĺ—Ā–Ĺ–ĺ–≤–ł—ā–Ķ –Ĺ–į —Ā–≤–ĺ—Ź —Ä–Ķ–ļ—É—Ä—Ā–ł–≤–Ķ–Ĺ (—Ą—Ä–į–ļ—ā–į–Ľ–Ķ–Ĺ) –ľ–Ķ—ā–ĺ–ī.
–ü—Ä–Ķ–∑ 1975 –≥. –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –≤—ä–≤–Ķ–∂–ī–į —ā–Ķ—Ä–ľ–ł–Ĺ–į "—Ą—Ä–į–ļ—ā–į–Ľ" (–ĺ—ā –Ľ–į—ā. Fractus, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į "—Ā—á—É–Ņ–Ķ–Ĺ–ĺ") –∑–į –ĺ–Ņ–ł—Ā–≤–į–Ĺ–Ķ –Ĺ–į —Ā—ā—Ä—É–ļ—ā—É—Ä–ł –ł –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā –ł–ī–Ķ–ł—ā–Ķ —Ā–ł –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ, –§—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ: –§–ĺ—Ä–ľ–į, –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā –ł —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā. (Fractals: Form, Chance and Dimension). –ú–į—ā–Ķ–ľ–į—ā–ł–ļ—ä—ā –°—ā–ł–≤—ä–Ĺ –í–ĺ–Ľ—Ą—Ä–į–ľ –Ņ–ĺ-–ļ—ä—Ā–Ĺ–ĺ –≥–ĺ –Ĺ–į—Ä–ł—á–į "–Ī–į—Č–į—ā–į –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ".¬†
–ü—Ä–Ķ–∑ 1977–≥. –Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā¬†–Ņ—É–Ī–Ľ–ł–ļ—É–≤–į ‚Äú–§—Ä–į–ļ—ā–į–Ľ–Ĺ–į—ā–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ĺ–į –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į‚ÄĚ (‚ÄúThe Fractal Geometry of Nature‚ÄĚ).
–ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā¬†–ł–∑–Ņ–ĺ–Ľ–∑–≤–į –Ĺ–į—É—á–Ĺ–ł—ā–Ķ —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł –Ĺ–į –ī—Ä—É–≥–ł —É—á–Ķ–Ĺ–ł, —Ä–į–Ī–ĺ—ā–Ķ—Č–ł –≤ –Ņ–Ķ—Ä–ł–ĺ–ī–į 1875-1925 –≥. –≤ —ā–į–∑–ł –ĺ–Ī–Ľ–į—Ā—ā (–ü–ĺ–į–Ĺ–ļ–į—Ä–Ķ, –§–į—ā—É, –Ė—é–Ľ–ł–į, –ö–į–Ĺ—ā–ĺ—Ä, –•–į—É—Ā–ī–ĺ—Ä—Ą, –ü–Ķ–į–Ĺ–ĺ).
–ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –ĺ–Ī–Ķ–ī–ł–Ĺ—Ź–≤–į —ā–Ķ—Ö–Ĺ–ł—ā–Ķ —Ä–į–Ī–ĺ—ā–ł –≤ –Ķ–ī–ł–Ĺ–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į. –ü–ĺ –Ĺ–Ķ–≥–ĺ–≤–ł—ā–Ķ –ī—É–ľ–ł: ‚ÄĚ...¬†–ľ–Ķ–∂–ī—ɬ†–Ĺ–Ķ–ļ–ĺ–Ĺ—ā—Ä–ĺ–Ľ–ł—Ä—É–Ķ–ľ–ł—Ź —Ö–į–ĺ—Ā –ł —Ā—ā—Ä–ĺ–≥–ł—Ź —Ä–Ķ–ī –Ĺ–į –ē–≤–ļ–Ľ–ł–ī –≤–Ķ—á–Ķ –ł–ľ–į –Ĺ–ĺ–≤–į –∑–ĺ–Ĺ–į ‚Äď —ā–į–∑–ł –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ‚ÄĚ.
–ö–į–ļ–≤–ĺ –Ķ —Ą—Ä–į–ļ—ā–į–Ľ?
–°–į–ľ–ł—Ź—ā –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ķ –≤–∑–Ķ–Ľ –ī—É–ľ–į—ā–į —Ą—Ä–į–ļ—ā–į–Ľ –ĺ—ā –Ľ–į—ā–ł–Ĺ—Ā–ļ–į—ā–į –ī—É–ľ–į fractus, –ļ–ĺ–Ķ—ā–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į, —Ā—á—É–Ņ–Ķ–Ĺ, —Ä–į–∑–Ī–ł—ā,¬†—Ä–į–∑–ī–Ķ–Ľ–Ķ–Ĺ –Ĺ–į —á–į—Ā—ā–ł (—Ą—Ä–į–ļ—ā—É—Ä–į, —Ą—Ä–į–ļ—Ü–ł—Ź –ł–ľ–į—ā —Ā—ä—Č–ł—Ź –ļ–ĺ—Ä–Ķ–Ĺ). –ē–ī–Ĺ–ĺ –ĺ—ā –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź—ā–į –∑–į —Ą—Ä–į–ļ—ā–į–Ľ –Ķ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–į —Ą–ł–≥—É—Ä–į, —Ā—ä—Ā—ā–ĺ—Ź—Č–į —Ā–Ķ –ĺ—ā —á–į—Ā—ā–ł –ł –≤—Ā—Ź–ļ–į –ĺ—ā –ļ–ĺ–ł—ā–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ, –Ņ–ĺ–Ĺ–Ķ –Ņ—Ä–ł–Ī–Ľ–ł–∑–ł—ā–Ķ–Ľ–Ĺ–ĺ –ļ–ĺ–Ņ–ł–Ķ –Ĺ–į —Ü—Ź–Ľ–ĺ—ā–ĺ. –§—Ä–į–ļ—ā–į–Ľ—ä—ā –Ķ —ā–į–ļ—ä–≤¬†–ĺ–Ī–Ķ–ļ—ā, –∑–į –ļ–ĺ–Ļ—ā–ĺ –Ĺ—Ź–ľ–į –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –Ņ–ĺ–ī –ļ–į–ļ—ä–≤ –ľ–į—Č–į–Ī –≥–ĺ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į–ľ–Ķ¬†-¬†—Ā—ā—Ä—É–ļ—ā—É—Ä–į—ā–į –ľ—É –ĺ—Ā—ā–į–≤–į —Ā—ä—Č–į—ā–į.¬†
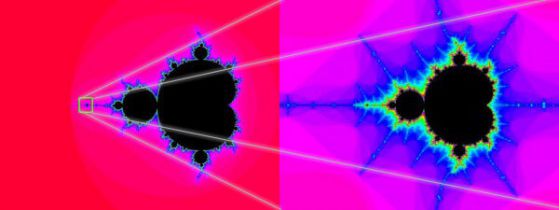
–í –ĺ—Ā–Ĺ–ĺ–≤–į—ā–į –Ĺ–į —ā–ĺ–≤–į —Ź–≤–Ľ–Ķ–Ĺ–ł–Ķ –Ķ –ľ–Ĺ–ĺ–≥–ĺ –Ņ—Ä–ĺ—Ā—ā–į –ł–ī–Ķ—Ź: –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–į—ā–į –ļ—Ä–į—Ā–ĺ—ā–į –ł —Ä–į–∑–Ĺ–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ –Ĺ–į –ľ–Ĺ–ĺ–≥–ĺ–∂–Ķ—Ā—ā–≤–ĺ —Ą–ĺ—Ä–ľ–ł –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–į—ā –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł –ĺ—ā —Ā—Ä–į–≤–Ĺ–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā –ľ–ĺ–ī–Ķ–Ľ¬†—Ā–į–ľ–ĺ —Ā –ī–≤–Ķ –ĺ–Ņ–Ķ—Ä–į—Ü–ł–ł - –ļ–ĺ–Ņ–ł—Ä–į–Ĺ–Ķ –ł –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ.
–Ę—ä–Ļ –ļ–į—ā–嬆–Ĺ—Ź–ľ–į —Ā—ā—Ä–ĺ–≥–į¬†–ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –ī–Ķ—Ą–ł–Ĺ–ł—Ü–ł—Ź –∑–į —Ą—Ä–į–ļ—ā–į–Ľ–ł, –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ –Ņ–ĺ–ī "—Ą—Ä–į–ļ—ā–į–Ľ" —Ā–Ķ —Ä–į–∑–Ī–ł—Ä–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ķ–Ĺ –ľ–ĺ–ī–Ķ–Ľ, –ļ–ĺ–Ļ—ā–ĺ –ł–ľ–į –Ķ–ī–Ĺ–ĺ –ł–Ľ–ł –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā –Ķ–ī–Ĺ–ĺ –ĺ—ā —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į:
- –ł–ľ–į —Ā–Ľ–ĺ–∂–Ĺ–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į –Ņ—Ä–ł –ļ–į–ļ–≤–ĺ—ā–ĺ –ł –ī–į –Ķ¬†—É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ;
- –Ķ —ā–ĺ—á–Ĺ–ĺ –ł–Ľ–ł –Ņ—Ä–ł–Ī–Ľ–ł–∑–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ;
- –ł–ľ–į –ī—Ä–ĺ–Ī–Ĺ–į (—Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–į)¬†—Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā, –ļ–ĺ—Ź—ā–ĺ –Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–į –ĺ—ā —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—á–Ĺ–į—ā–į;
- –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł¬†–ĺ—ā –Ņ—Ä–ĺ—Ā—ā –ł—ā–Ķ—Ä–į—Ü–ł–ĺ–Ĺ–Ķ–Ĺ –ł —Ä–Ķ–ļ—É—Ä—Ā–ł–≤–Ķ–Ĺ —Ü–ł–ļ—ä–Ľ. –Ę–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ –Ĺ–į —Ā—ä–∑–ī–į–≤–į–Ĺ–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź —Ā–≤–ĺ–Ļ—Ā—ā–≤–į—ā–į –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ¬†–ł¬†–ī—Ä–ĺ–Ī–Ĺ–į —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā.
–ě—Ā–Ĺ–ĺ–≤–Ĺ–ł –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –ł –Ľ–Ķ–ļ—Ā–ł–ļ–į
- –§—Ä–į–ļ—ā–į–Ľ–ł
- –Ņ—Ä–į—Ö –Ĺ–į –ö–į–Ĺ—ā–ĺ—Ä
- –Ņ–Ķ—ā–ĺ—ä–≥—ä–Ľ–Ĺ–ł–ļ (–Ņ–Ķ–Ĺ—ā–į–≥–ĺ–Ĺ) –Ĺ–į –ź–Ľ–Ī—Ä–Ķ—Ö—ā –Ē—é—Ä–Ķ—Ä
- –Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā
- —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ
- –ī—Ä–ĺ–Ī–Ĺ–į (—Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–į)¬†—Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā
- –ł—ā–Ķ—Ä–į—Ü–ł—Ź
- —Ä–Ķ–ļ—É—Ä—Ā–ł—Ź
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
–§—Ä–į–ļ—ā–į–Ľ—Ć–Ĺ–į—Ź –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź –Ņ—Ä–ł—Ä–ĺ–ī—č, –ú–į–Ĺ–ī–Ķ–Ľ—Ć–Ī—Ä–ĺ—ā –Ď.
Fractal Geometry, Yale University, Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger
–ß—ā–ĺ —ā–į–ļ–ĺ–Ķ —Ą—Ä–į–ļ—ā–į–Ľ—č, –ē–≤–≥–Ķ–Ĺ–ł–Ļ –ē–Ņ–ł—Ą–į–Ĺ–ĺ–≤
–•–ź–ě–°, –§–†–ź–ö–Ę–ź–õ–ę –ė –ė–Ě–§–ě–†–ú–ź–¶–ė–Į –Ē–ĺ–ļ—ā–ĺ—Ä —Ą–ł–∑–ł–ļ–ĺ-–ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—Ö –Ĺ–į—É–ļ –ź. –Ē–ú–ė–Ę–†–ė–ē–í,

























–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
02.02 2015 –≤ 09:24
02.02 2015 –≤ 08:44
15.01 2015 –≤ 16:28
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
YKoshev
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ
dolivo
–°–į—Ö–į—Ä–į –ĺ—á–į–ļ–≤–į 75% —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–į–Ľ–Ķ–∂–ł—ā–Ķ –ī–ĺ 2100 –≥.
dolivo
–ó–Ķ–ľ–Ĺ–į—ā–į —Ź–Ī—ä–Ľ–ļ–į: —Ā—ā–į—Ä–į –ļ—É–Ľ—ā—É—Ä–į –∑–į –Ĺ–ĺ–≤–ł—ā–Ķ –ļ–Ľ–ł–ľ–į—ā–ł—á–Ĺ–ł –≤—Ä–Ķ–ľ–Ķ–Ĺ–į
dolivo
–ó–Ķ–ľ—Ź—ā–į –Ņ–ĺ—ā—ä–ľ–Ĺ—Ź–≤–į. –ö–į–ļ–≤–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į —ā–į–∑–ł —ā—Ä–Ķ–≤–ĺ–∂–Ĺ–į –ļ–Ľ–ł–ľ–į—ā–ł—á–Ĺ–į —ā–Ķ–Ĺ–ī–Ķ–Ĺ—Ü–ł—Ź –∑–į –Ī—ä–ī–Ķ—Č–Ķ—ā–ĺ?