Ако лъв преследва стадо антилопи, какви правила регулират поведението на стадото? Теорията на егоистичното стадо и геометрията могат да покажат как се развиват сложни поведения в реалността на базата на прости правила.
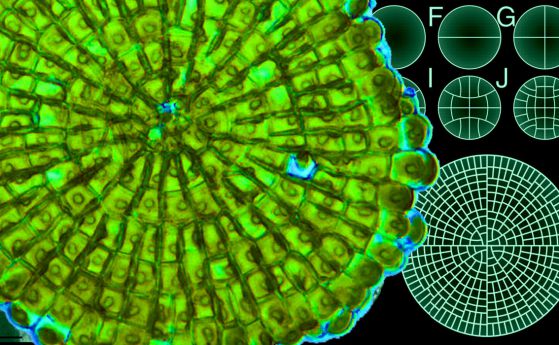
Вместо да действа в полза на групата като цяло, всяка антилопа се позиционира така, че има най-малко едно друго животно между нея и хищника. Това произвежда модел, известен като мозайка на Вороной (Диаграма на Вороной) - всяка точка в схемата горе е антилопа, а заобикалящият я цветен многоъгълник е участък, всяка точка от който е по-близо до дадения индивид, отколкото до всеки друг. Ако лъвът влезе в тази зона, тогава антилопата ще бъде изядена, разказва сайтът Futility Closet.
Този математически модел помага да се обясни някои стадни поведения. Всяко животно иска да направи своята "зона на опасност" (заобикалящия го цветен многоъгълник) възможно най-малка и да бъде, доколкото е възможно, по-далече от хищника. Доминиращите животни са склонни да се позиционират в близост до центъра, подчинените животни се изтласкват в периферията като цялата формация се развива непрекъснато в хода на движенията на стадото и хищника.
Още за "егоистичното" стадо
Много от предполагаемите ползи от груповия начин на живот се дължи на факта, че така е по-лесно да се избегне нападение от хищници. Една такава теория е формулирана от Уилям Хамилтън в работата му "Геометрия на егоистичното стадо", а според Докинс и неговата "теория за егоистичния ген", по-скоро трябва да имаме предвид "стадо от егоистични индивиди".
Хищникът винаги ще се опитва да атакува най-близката до него антилопа и тази стратегия е разумна от негова гледна точка, защото позволява да се намалят до минимум разходите на енергия. От гледната точка на жертвата, тази стратегия предполага интересна последица: всеки отделен индивид-жертва винаги ще се стреми да не бъде най-близо до хищника. Ако жертвата успее да открие предварително хищника, тя просто побягва. Но ако хищникът се появи неочаквано, например от висока трева, където се криел, всяка жертва все още може да намали шансовете си да бъде най-близо от всички до хищника. Можем да си представим, че всяка жертва, като че ли е заобиколена от "зона на опасност".
Така например, ако индивидите-жертви се движат на известно разстояние един от друг, образувайки правилна геометрична фигура, то опасната зона около всеки един от тях (освен ако не се намират накрая), може да има приблизително шестоъгълна форма. Особено уязвими са идивидите, които са в краищата на стадото, тъй като зоната на опасност не се ограничава до един сравнително малък шестоъгълник, а включва обширна област, в непосредствена близост до откритата му страна.
Ясно е, че един разумен индивид ще се опита да направи своята опасна зона да е възможно най-малка. На първо място, ще избягва да се намира в края на на стадото. Веднъж оказал се накрая, той веднага започва да се опитва да се премести към центъра. За съжаление, някой винаги трябва да бъде накрая, но всеки индивид се стреми този “краен” да не бъде той!
Снимка: tploy.com
Съществува непрекъсната миграция на индивиди от периферията към центъра. Ако стадото в началото е било рехаво и разпръснато, то скоро се уплътнява в компактна маса, в резултат на вътрешната миграция. Дори ако в началото в рамките на модела не се забелязва никаква тенденция към скупчване и животините-жертви първоначално да са разпръснати, всеки индивид ще бъде обхванат от егоистичния стремеж да намали своята зона на опасност като се опита да заеме място в пролуките между другите индивиди. Това бързо води до образуването на струпвания (агрегации), които ще стават все по-плътни.
Очевидно е, че в реалния живот, тенденцията към образуването на струпвания ще бъде ограничена от натиска, насочен в обратна посока: в противен случай всички индивиди ще се струпат в една купчина! Въпреки това, този модел е интересен, защото показва, че дори изхождайки от много прости предположения може да се стигне до модели в реалния свят.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари