
През 1918 г. двама германски математици от гьотингенската школа публикували творби, имащи огромно значение за съвременната физика. Една от най-блестящите алгебристки на ХХ век Еми Ньотер представя доказателства на две значими днес теореми, свързващи законите за съхранението на различни величини (енергия, импулс, заряд и т.н.) със свойствата на пространство-времето (хомогенност, изотропност, равномерност на хода на времето и др.). Тези теореми станали мощно и универсално средство за извеждане на подобни закони в нютоновата и релативистка механика, в теорията на притеглянето, електродинамиката, квантовата теория на полето и физиката на елементарните частици.
Статията на германския физик и философ Херман Вайл (1885-1955) "Гравитация и електричество", публикувана в Берлин, е доста по-малко известна. Тя и нейното продължение, издадено една година по-късно, поставили началото на по-ефективен подход в конструирането на теорията за микросвета, а този подход бил вече готов във втората половина на ХХ век. Била създадена обединена теория на трите фундаментални взаимодействия – силното, слабото и електромагнитното – наречена Стандартен модел.
От силите към потенциалите

Херман Вайл (1885-1955)
Както е логично да се очаква, и Херман Вайл имал предшественици. В началото на ХІХ век работите на няколко математици, особено място между които имат Гаус, Стокс и Поасон, преобразували математическия апарат на Нютоновата теория за притеглянето.
В новата интерпретация тя представлявала силово поле, пронизващо Вселената. Това поле започнали да описват като притежаващо гравитационен потенциал – скаларна функция, зависеща от пространствените координати, но не и от времето. При това силата на притегляне в произволна точка се определяла от това, колко рязко се изменя близо до нея този потенциал (тоест градиентът му).
Това нововъведение обогатило математическия апарат на небесната механика и други области на физиката, които се занимават с гравитацията, но внесло в описанието й някаква неопределеност. В Нютоновия и Кулоновия закони фигурират сили на притегляне, които могат да бъдат непосредствено измерени, и те се определят еднозначно (в избрана система от мерни единици).
В същото време потенциалът е определен с точност до адитивна константа – значение има градиентът му. В онези времена това изглеждало като тривиално следствие на математическия формализъм, без отношение към истинската физика.
Столетия по-късно по такъв начин пренаписали класическата електродинамика. Първоначално тя била представяна с уравненията на Максуел, в които влизат измерваните напрегнатости (интензитети или индукции) на електрическото и магнитното полета. Тези уравнения също е удобно да се изразят чрез потенциал, но по-сложен, отколкото този на Нютоновата гравитация (освен скаларната част, в него влиза вектор, определящ величината на магнитното поле).
Уравненията на електродинамиката, изразени по такъв начин, изглеждат твърде елегантно и се свързват с пространство-времето посредством Специалната теория на относителността. Особен принос за установяването на тези връзки има холандският физик Хендрик Лоренц. Обаче те стават нееднозначни, понеже напр. към векторния потенциал може да се добави кой да е постоянен вектор, а към скаларния – произволно число.
Също така, тези добавки могат да се изменят и в пространството, и във времето, ако те са правилно свързани една с друга, тъй като свободата на избор в електромагнитните потенциали е по-голяма в сравнение с Нютоновата гравитация. Физиците и математиците от началото на ХХ век прекрасно виждали тази нееднозначност, но, както и предшествениците им, не й придавали особено значение.
Калибровъчни преобразувания
Това свойство на електромагнитните потенциали има дълбок физически смисъл. Техните взаимни изменения се компенсират точно по такъв начин, че да се съхранят в предишния им вид уравненията на Максуел.
Нееднозначността на избора фактически отразява неразривната връзка между електричеството и магнетизма.
Преобразуванията на потенциалите, неизменящи уравненията на електромагнитното поле, се наричат калибровъчни (този термин също тръгва от статията на Вайл). Според физиците тези уравнения са инвариантни по отношение на калибровъчните преобразувания. В квантовата електродинамика такава непроменимост, в съответствие с теоремата на Ньотер, води след себе си закона за съхранение на електрическия заряд.
В такъв смисъл, калибровъчната инвариантност, въпреки своя привидно формален характер, открива възможност за заключение с напълно физически смисъл!
И то не само по отношение на електромагнетизма. Принципът на еквивалентността, на който се базира общата теория на относителността (ОТО) гласи, че гравитационното поле създава същите физически ефекти, каквито и ускорението (т.е. промяната на импулса на тялото). Ако недалеч от космически кораб с работещ двигател се разположи гравитационна маса, по принцип може напълно да се компенсира импулсът на двигателя и дъ се създаде в кабината зона на безтегловност.
Такава компенсация на ускоренишето чрез променлив гравитационен потенциал е аналогична на взаимната ковпенсация на измененията на потенциалите на електромагнитното поле. Това навежда на мисълта, че уравненията на общата теория на относителността трябва да се подчиняват на нещо твърде подобно на калибровъчни преобразувания.
Такива разсъждения сега изглеждат напълно естествени, но преди стотина години до тях достигали малцина. Калибровъчната инвариантност – и като идея, и като термин – дошла в практическата физика по друг път. За да разберем как е станало това, нека се обърнем към работите на Вайл.
Светът на променливите мащаби
Уравненията на гравитационното поле в пространството Вайл записал с геометрия, различна от тази, който използвал Айнщайн. Добавени били формули, в които Вайл забелязал основните части на уравнението на Максуел. По този път той получил математическа конструкция, която сметнал за единна теория за електричеството и притеглянето.
Уравненията на ОТО се записват в Риманово пространство, представляващо изкривено четириизмерно времепространство с еднозначна метрика. За разлика от "плоското" евклидово пространство, където при успоредно пренасяне (транслация) на произволен вектор заедно със затворена крива при връщане в изходна точка той ще се окаже в първоначална позиция, в Римановото пространство такова пренасяне ще се завърши с изместване на вектора на ненулев ъгъл, който ще бъде мярка за кривината на пространството в тази точка. От друга страна, дължината на вектора след преноса ще остане същата – в това се и състои еднозначността на метриката.
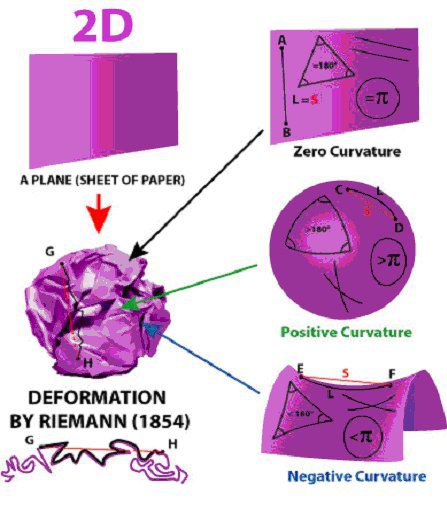
Риманов опит от 1854 - вписване на три традиционни вида геометрично изкривяване в една структура
От това ограничение Вайл се отказал. Той предположил, че уравненията на притеглянето не трябва да зависят от мащабите, прилагани за измерване на дължината. Във всекидневния живот с еднакъв успех се използвали единици като метър, фут, че дори и аршин. Числовите значения на дължината на всеки отрязък зависят от единиците за измерване, но отношенията помежду им строго се съхраняват.
Нещо подобно се получава и във Вайловата геометрия, само мащабовата единица постоянно се изменя от точка на точка. След нея се изменят и дължините, но отношението на тези дължини към всяка двойка вектори с общ произход остава неизменно. Операцията по смяната Вайл нарекъл прекалибровка. Тя съхранява уравнението на гравитационното поле – това е именно калибровъчната инвариантност в ранния й период на съществуване.
Но какво прави тук електричеството? В ОТО дължините на векторите се запазват, затова и тяхното сравнение не представлява проблем. А сега на Вайл му дошло наум да въведе математически правила, позволяващи да се изясни имат ли два вектора в съседни точки еднаква дължина (макар че при това самата дължина не е нужно да бъде определена!).
Тези правила той интерпретирал като уравнения на Максуел за електромагнитните потенциали. Измененията на дължините на вектора се определят именно от тези потенциали (подобно на това как изменението на ориентацията му се задава от кривината на пространството, която се проявява като гравитация).
Вайл изпратил ръкописа на статията си на Айнщайн и го помолил да я препоръча за публикуване. Айнщайн така и направил, но отбелязал, че ако теорията на Вайл е вярна, то честотите на емисионните оптични спектри трябва да зависят от историята на излъчилите атоми, а това противоречало на експериментите до момента. Били повдигнати и други възражения и те в края на краищата поставили кръст на Вайловото обединение на електричеството и гравитацията. Изумителният по красотата си физичен модел се оказал именно физически несъстоятелен.
Обаче по-късно станало ясно, че идеята за калибровъчната инвариантност е сериозна и конструктивна, а Вайл се излъгал само в нейното конкретно приложение. През 20-те г. това разбpали неколцина физици, в това число и Фриц Лондон – впоследствие един от авторите на първата квантова теория за свръхпроводимостта. През 1927 г. той предложил нова интерпретация на Вайловата теория, правейки я част от квантовата физика.

Фриц Лондон (1900-1954)
Проблемът с гравитацията
Обаче гравитацията, с която всъщност започва всичко, не влиза в очертания в началото Стандартен модел.
По думите на руския квантов физик акад. Валерий Рубаков, гравитацията има своя специфика: "При квантуването на гравитационното поле възникват гравитони. Това също са бозони, но вече не векторни – техният спин е вече не единица, а двойка. Обаче теорията на гравитацията отново се подчинява на калибровъчната симетрия.

Гравитонът, подобно на фотона, има само две поляризации, а в същото време математически възможните поляризации у частиците със спин двойка са пет на брой. Калибровъчната симетрия на гравитационното поле позволява да се премахнат излишните (от физически съображения) поляризации, като по този начин се направи теорията непротиворечива с наблюдаваната действителност.
Тази симетрия е забелязал още Айнщайн, макар в ОТО да няма никакви гравитони. Но там има симетрия в пространство-времето по отношение на всички гладки преобразувания на координатите, а това е всъщност калибровъчна симетрия. Оказва се много сложно да се обединят сегашните теории на елементарните частици с гравитацията, и в това е очевидната слабост на тези теории. Всички опити да се създаде квантова теория на гравитацията още не са се увенчали с успех. Така че нашите днешни калибровъчни модели все още не са цялата истина.
Аз мисля, че за обединено описание на всичките четири основни взаимодействия трябва да се изобрети нова теория с още по-широка калибровъчна симетрия. Мнозина възлагат големи надежди на теорията за суперструните, но по-вероятно е да е нужно нещо дори по-широко. Някои нейни черти се забелязват още сега, но кога те ще се появят и каква форма ще имат, аз не се наемам да предскажа".
Фазата
Ето как изглежда идеята на Лондон в съвременно изражение. Квантовите обекти се описват с комплексна (в математически смисъл) вълнова функция. Да се измери тя опитно (както и електромагнитните потенциали) е практически невъзможно.
По експериментален път се изясняват само вероятностите на стойностите на физичните величини, които се определят чрез квадрата на модула на тази вълнова функция. Поради това тя може да се умножи по всяко комплексно число с единичен модул – вероятността не се изменя от това. Ако се представи такова число като експонента с чисто фиктивен показател, то операцията на неговото умножение с вълновата функция ще доведе до изменение на неговата фаза (по известната формула на Ойлер).
Ако на квантовата частица на действат никакви сили, изменението на фазата няма да повлече със себе си никакви особени последствия. Движението на заредената частица в електромагнитно поле в нерелативисткия случай се изразява с уравнението на Шрьодингер, което в общия случай не е инвариантно по отношение на изменението на фазовия множител.
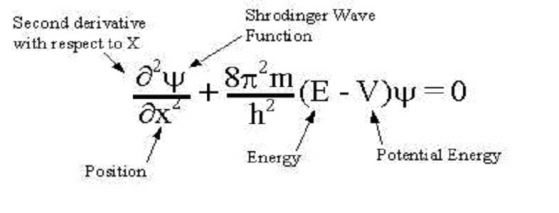
Това затруднение може да се избегне, ако едновременно се изменят електромагнитните потенциали с помощта на същото онова класическо преобразуване, което след работите на Вайл било наречено калибровъчно. Ако се запише показателят на експонентата като произведение на фиктивна единица за заряда на частицата и скаларна функция на времето и координатите, то тази функция ще покаже нужното калибровъчно преобразуване на потенциалите.
То точно компенсира онези допълнителни условия в уравнението на Шрьодингер, които се появяват след промяната на фазата на вълновата функция.
Къде е физичният смисъл на тази чисто абстрактна математика? Състоянията на частиците, чиито вълнови функции се различават само по фазови множители, от гледна точка на експеримента са еквивалентни.
Ако частицата е заредена и, следователно, взаимодейства с електромагнитото поле, възможността за произволна смяна на фазовия множител се осигурява от съответното изменение на електромагнитите потенциали. Уравнението за движението на частицата е инвариантно по отношение на избора на фаза на вълновата функция. А това автоматично води до калибровъчна инвариантност на полевите уравнения.
Ако уравнението на Шрьодингер за заредената частица се запише без каквито и да е електромагнитни потенциали, намери се неговото решение във вид на вълнова функция и се умножи тя по фазовия множител, в уравнението се появяват допълнителни условия. Следователно, то трябва да съдържа компоненти, които чрез своите изменения биха компенсирали нововъзникващите добавки. В качеството на такива компоненти се явяват електромагните потенциали.
Излиза, че ако вълновите функции, различаващи се по произволен фазов множител описват едно и също състояние на заредената квантова частица, то трябва да съществуват и електромагнитни полета, подчиняващи се на уравненията на Максуел.
По такъв начин ние дойдохме до удивителен резултат – фазовата инвариантност поражда електромагнетизъм! Това у Лондон не присъства, макар логиката на неговите разсъждения да навежда на подобни мисли. Първият учен, ясно формулирал такъв извод, е именно Вайл в статията "Електрон и гравитация", публикувана през 1929 г. (макар че той използвал не уравнението на Шрьодингер, а Дираковото уравнение за релативисткия електрон). Умножението на вълновата функция по фазовия множител у Вайл представлява ново калибровъчно преобразуване, тясно свързано с преобразуването на електромагнитните потенциали.

Първото издание на "Електрон и гравитация", 1929 г.
Инструмент за предсказания
Идеите на Вайл така привлекли Волфганг Паули, че през 1933 г. той ги предсказал в статията си "Вълнова механика". В средата на 40-те г. ги прочел младият китайски физик Янг Цзенин, когото много заинтригувало доказателството за връзката между фазовата инвариантност и съхранението на електрическия заряд.
През 1953-54 г. в Националната лаборатория в Брукхейвън (САЩ) Цзенин и аспирантът Робърт Милс приложили тези идеи за анализ на ядрените сили. Тяхната съвместна статия "Съхранение на изотопичния спин и обобщената каибровъчна инвариантност" изиграла огромна роля в развитието на теоретичната физика.
Янг и Милс първи доказали, че на основата на калибровъчна симетрия може да се предскаже съществуването на неизвестни по-рано физични полета и, като следствие на това, на още неоткрити частици. Една година след това Паули дошъл до аналогични изводи, но се въздъражл да ги публикува. През 60-те и 70-те г. този ръст дал обилен принос в Стандартния модел на елементарните частици.
Валерий Рубаков допълва: "Всички основни взаимодействия, с изключение на гравитацията, се пренасят с векторни частици – така е устроен светът. А при такова положение е просто необходимо да се работи с калибровъчни симетрии, иначе се получават откровени патологии.
Към разбирането на тези неща физиците изминали различни пътища. Калибровъчната природа на електромагнетизма е известна още от времената на Вайл. Обединената калибровъчна теория на слабите и електромагнитни взаимодействия беше развита от Стивън Уайнбърг и Абдус Салам през втората половина на 60-те г. и окончателно доработена едва в началото на 70-те. А след това дойде редът и на вътреядрените сили. Тогава експериментаторите показаха, че на много малки разстояния взаимодействието между кварките не нараства, а отслабва.
Това явление беше наречено асимптоматична свобода, и отначало то не намери разумно обяснение. Обаче трима физици-теоретици – Дейвид Грос, Франк Уилчек и Дейвид Полицер – скоро доказаха, че в калибровъчните модели на глуонните полета асимптоматичната свобода възниква по естествен път. Оттам нататък остана кратък път до обединението на теориите за електрослабите и силните взаимодействия в единната теоретична конструкция "Стандартен модел".
Симетрията: глобална и локална

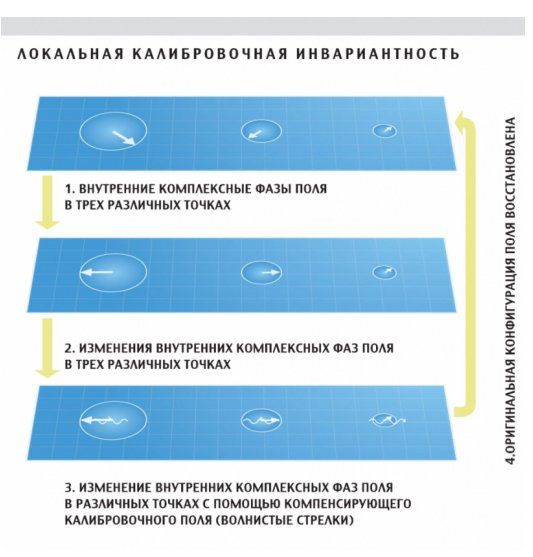
Комплексната вълнова функция на всяка квантова частица може да се представи като вектор, посоката на който отпределя фазата на частицата. Глобалната симетрия означава, че ако векторите, съответстващи на всички частици, запълващи пространството, се завъртят на еднакъв ъгъл около дадена произволна ос, законите на физиката не се променят. А калибровъчната симетрия е локално преобразуване, индивидуално обръщане на фазата на всяка частица.
В калибровъчните теории съществува много обширна симетрия, която се проявява по различен начин в различно време и пространство. Поради това при математическото описание на симетрии от такъв вид възникват параметри, които зависят от пространствено-времевите координати. И се оказва, че съществуването на калибровъчните симетрии налага много силни ограничения върху свойствата на обектите, които тези теории описват.
Групите на симетрия и калибровъчните бозони: от абстракция към реалност
В теоретичната физика инвариантността по отношение на определени преобразувания довежда до появата на особени свойства. Така например, Нютоновото уравнение за движение е инвариантно по отношение на транслацията (изместване на някакво разстояние в пространството), а това влече закона за съхранение на импулса. Калибровъчните преобразувания на пръв поглед изглеждат абстрактни, но те показват съществуването на различни калибровъчни полета, свързани с математическото понятие "групи на симетрия". Теорията на групите води началото си от разсъжденията на забележителния френски математик Е. Галоа, като едва в началото на ХХ век привлича заслужено внимание.
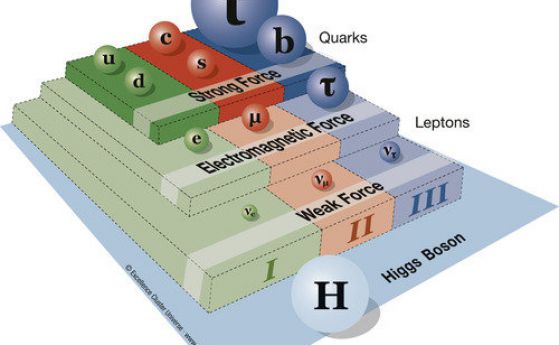
Например, в групата U (1) има само един фазов ъгъл. В Стандартния модел (СМ) му съответства един бозон (на електромагнитното взаимодействие – фотон), групата SU (2) има три фазови ъгъла (в СМ – три бозона на слабото взаимодействие), в SU (3) – осем фазови ъгъла (осем бозона на силното взаимoдействие – глуони).
Антон Оруш, Sandacite.net – www.sandacite.net
Източници
Geometry and the Riemann Space
Svozil, Karl - Mathematical Methods of Theoretical Physics
What is the Schrodinger equation, and how is it used?





















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон