
Математиката е видима навсякъде в природата, дори там, където не я очакваме. Това може да помогне да се обясни начина, по който галактиките се оформят спираловидно, кривите на раковината и реките се извиват.
Дори субективните емоции, като това, което намираме за красиво, могат да имат математически обяснения.
„Не само математиката изглежда красива – красотата е и математическа. Двете са преплетени“, отбелязва д-р Томас Бриц (Thomas Britz), преподавател във факултета по математика и статистика на Университета на Нов Южен Уелс, Сидни, Австралия.
Д-р Бриц работи в областта на комбинаториката, клон на математиката, посветен на решаването на задачи, свързани с избора и подреждането на елементи от определено (най-често крайно) множество в съответствие с дадени правила. Докато комбинаториката е в рамките на чистата математика, д-р Бриц винаги е бил привлечен от философските въпроси за математиката.
Той също така намира красота в математическия процес.
„От лична гледна точка математиката е наистина забавна. Обичам я още от малък.
„Понякога красотата и удоволствието от математиката са в концепциите, понякога - в резултатите, понякога - в обясненията. Друг път мисловните процеси карат ума ви да се обърка по хубав начин, емоциите, които получавате, или просто да работите увлечени - като да потънете в хубава книга."
Тук д-р Бриц споделя някои от любимите си връзки между математиката и красотата.
1. Симетрия - но с нотка на изненада
През 2018 г. д-р Бриц изнася за TEDx лекция за математиката на емоциите, където използва последните проучвания върху математиката и емоциите, за да се докосне до това как математиката може да помогне за обяснението на емоциите, като красотата.
 Симетрията е навсякъде, където погледнете. Кредит: Unsplash
Симетрията е навсякъде, където погледнете. Кредит: Unsplash
„Нашият мозък ни възнаграждава, когато разпознаваме закономерности (патерни) или виждаме симетрия, организираме на части от едно цяло или решаваме пъзели“, коментира д-р Бриц.
"Когато забележим нещо, което се отклонява от закономерностите - когато има докосване на неочакваното - нашите мозъци ни възнаграждават отново. Изпитваме наслада и вълнение."
Например, хората възприемат симетричните лица като красиви. Но особеноест, която нарушава симетрията по малък, интересен или изненадващ начин - като бенка - добавя към красотата.
„Същата идея може да се види в музиката“, обяснява д-р Бриц. „Моделираните и подредени звуци с нотка на изненада могат да добавят индивидуалност, чар и дълбочина.“
Много математически концепции показват подобна хармония между закономерност и изненада, елегантност и хаос, истина и загадка.
„Преплитането на математика и красота само по себе си е красиво за мен“, отбелязва д-р Бриц.
 Всяко листенце от папрат стига до по-малки версии на себе си. Кредит: Rawpixel (CC0 1.0)
Всяко листенце от папрат стига до по-малки версии на себе си. Кредит: Rawpixel (CC0 1.0)
2. Фрактали: безкрайни и призрачни
Фракталите са модели (патерни), които се повтарят до известна степен в по-малки мащаби. Колкото по-отблизо се вглеждаме, толкова повече повторения ще видим - като листата на папрат.
„Тези повтарящи се модели са навсякъде в природата“, разказва д-р Бриц. „В снежинки, речни мрежи, цветя, дървета, светкавици – дори в кръвоносните ни съдове.

Фракталите в природата често могат да се репликират само от няколко степени, но теоретичните фрактали могат да бъдат безкрайни. Много компютърно генерирани симулации са създадени като модели на безкрайни фрактали.
 Триъгълникът (решетката, салфетката) на Серпински е измислен от полския математик Вацлав Франциск Серпински през 1915г. Серпински е учен с изключителен принос към теорията на множествата, теорията на числата, теорията на функциите и топологията. Тази анимация показва ясно точното самоподобие в този фрактал - триъгълника на Серпински Триъгълникът (решетката, салфетката) на Серпински е измислен от полския математик Вацлав Франциск Серпински през 1915г. Серпински е учен с изключителен принос към теорията на множествата, теорията на числата, теорията на функциите и топологията. Тази анимация показва ясно точното самоподобие в този фрактал - триъгълника на Серпински |
„Можете да продължите да се фокусирате върху фрактал, но никога няма да стигнете до края му“, обяснява д-р Бриц.
„Фракталите са безкрайно дълбоки. Те също така са безкрайно призрачни.
„Може да имате цяла страница, пълна с фрактали, но общата площ, която сте начертали, все още е нула, защото това е просто куп безкрайни линии.“
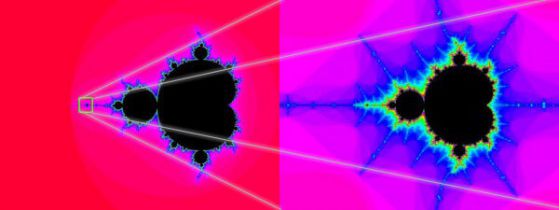 Сетът на Манделброт е може би най-известният компютърно генериран фрактал. Увеличаването ще разкрие точно същото изображение в по-малък мащаб – шеметен и хипнотичен безкраен цикъл.
Сетът на Манделброт е може би най-известният компютърно генериран фрактал. Увеличаването ще разкрие точно същото изображение в по-малък мащаб – шеметен и хипнотичен безкраен цикъл.
3. Пи: непознаваема истина
Пи (или „π“) е число, което често се научава за първи път в геометрията в гимназията. Най-просто казано, това е число малко повече от 3 или около 3.14.
Пи се използва най-вече при работа с окръжности като например изчисляване на обиколката на кръг с помощта само на неговия диаметър.
Но π е много повече от това.
„Когато се вгледате в други аспекти на природата, изведнъж ще откриете π навсякъде“, разказва д-р Бриц. „Не само, че е свързан с всеки кръг, но и π понякога се появява във формули, които нямат нищо общо с кръговете, като вероятността и математическия анализ.“
Въпреки че е най-известното число (Международният ден на Пи се провежда ежегодно на 14 март, 3.14 в американския начин на изписване на датите), около него има много мистерия.
„Ние знаем много за π, но всъщност нищо не знаем за π“, коментира д-р Бриц.
"Има красота в това - красива дихотомия или напрежение."
 Пи е свързано с океана и звуковите вълни чрез реда на Фурие, формула, използвана в ритмите и циклите. Кредит: Unsplash
Пи е свързано с океана и звуковите вълни чрез реда на Фурие, формула, използвана в ритмите и циклите. Кредит: Unsplash
Пи е безкрайно и по дефиниция непознаваемо. Все още не е идентифицирана закономерност след десетичната запетая. Разбираемо е, че всяка комбинация от числа, като вашия телефонен номер или рожден ден, ще се появи някъде в π (можете да търсите това чрез онлайн инструмент за търсене на първите 200 милиона цифри).
В момента знаем 50 трилиона цифри на π, рекорд, счупен по-рано през 2020 г.Но тъй като не можем да изчислим точната стойност на π , никога не можем да изчислим напълно обиколката или площта на кръга - въпреки че можем да се приближим.
"Какво става тук?", коментира д-р Бриц. „Какво има в това странно число, което по някакъв начин свързва всички кръгове по света?
"Има някаква загадка в основата на π, която не разбираме. Тази мистика го прави още по-красиво."
4. Златно и древно съотношение
Златното съотношение (или „ϕ“) е може би най-популярната математическа теорема за красотата. Счита се за най-естетически приятен начин за пропорция на обект.
Съотношението може да бъде съкратено приблизително до 1,618. Когато се представи геометрично, съотношението създава Златния правоъгълник или Златната спирала.
„През цялата история съотношението се е третирало като еталон за идеалната форма, независимо дали в архитектурата, произведенията на изкуството или човешкото тяло“, разказва д-р Бриц. „Наричано е „Божествена пропорция“.
Златната спирала често се използва във фотографията, за да помогне на фотографите да рамкират изображението по естетически приятен начин. Кредит: Видео - ръководство за фотографи.
"Много известни произведения на изкуството, включително на Леонардо да Винчи, се основават на това съотношение."
Златната спирала се използва често днес, особено в изкуството, дизайна и фотографията. Центърът на спиралата може да помогне на художниците да рамкират фокусните точки на изображението по естетически приятни начини.
5. Парадокс, по-близък до магията
Непознаваемата природа на математиката може да изглежда по-близо до магията.
Известна геометрична теорема, наречена парадоксът на Банах-Тарски, казва, че ако имате топка в 3D пространство и я разделите на няколко конкретни части, има начин да съберете отново частите, така че да създадете две топки.
„Това вече е интересно, но става още по-странно“, отбелязва д-р Бриц.
„Когато двете нови топки бъдат създадени, и двете могат да бъдат със същия размер като първата топка.“
Математически казано, тази теорема работи - възможно е да се сглобят отново парчетата по начин, който удвоява топките.
 Илюстрация на парадокса на Банах-Тарски. Кредит: Wikimedia Commons
Илюстрация на парадокса на Банах-Тарски. Кредит: Wikimedia Commons
Този парадокс често се описва неофициално като „грахово зърно може да бъде нарязано и сглобено отново като Слънцето“.
Теоремата се нарича парадокс, защото противоречи на базовата геометрична интуиция. „Удвояването на кълбо“ чрез разделянето му на части и сглобяването им чрез завъртания и премествания, без никакво разтягане, огъване или добавяне на нови точки, изглежда невъзможно, тъй като всички тези операции трябва, интуитивно, да запазят обема. Интуицията, че подобни операции запазват обема, не е математически абсурдна и дори е включена във формалната дефиниция на обемите. Това обаче не е приложимо тук, тъй като в този случай е невъзможно да се дефинират обемите на разглежданите подмножества. Повторното им сглобяване възпроизвежда набор, който има обем, който се оказва различен от обема в началото.
Удвояването на кълбо, въпреки че изглежда много съмнително от гледна точка на интуицията (всъщност не може да направите два от един портокал с помощта на нож), въпреки това не е парадокс в логическия смисъл на думата, тъй като това не води до логическо противоречие, подобно на това как така нареченият парадокс на бръснаря (Парадокс на Ръсел) води до логическо противоречие.
 Удвояването на топки е невъзможно - нали? Кредит: Unsplash
Удвояването на топки е невъзможно - нали? Кредит: Unsplash
„Не можете да направите това в реалния живот“, казва д-р Бриц. „Но можете да го направите математически.
"Това е нещо като магия. Това е магия."
Фракталите, парадоксът на Банах-Тарски и π са само повърхността на математическите понятия, в които има красота.
„За да усетите много красиви части от математиката, имате нужда от много основни познания“, обяснява д-р Бриц. „Имате нужда от много основни - и често много скучни - тренировки. Това е малко като да направите милион лицеви опори, преди да упражнявате спорт.
"Но си заслужава. Надявам се, че повече хора ще стигнат до забавната част от математиката. Има толкова много повече красота за разкриване."
Източник: The mystique of mathematics: 5 beautiful math phenomena
Sherry Landow, University of New South Wales






















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон