
В света на математиката има сензация - открита е нова форма петоъгълници, които покриват една равнина плътно, без пролуки и без припокриване. Това е само 15-ият вид петоъгълник, който може да прави това и първият, открит в последните 30 години.
Задачата за изпълване на пространството с еднообразни фигури е идея, която се е развивала от древните египтяни и гърци до наши дни. Това е идея, която носи дълбокия смисъл за начините на експанзия на порции, за възможния строеж на веществото и структурата на пространството
Това е икономическа задача - максимум резултат с минимум енергия и материал - да се скрои плат без много остатъци, да се покрие тротоара по-ефективно, с минимум разтвор между плочките - задача, която между впрочем, пчелите са решили блестящо - с правилни шестоъгълници. Освен с тях, една равнина може да се покрие плътно е еднакви триъгълници и четириъгълници във всякаква форма.
Но ето, че с петоъгълниците нещата са по-сложни, но и по-интересни.
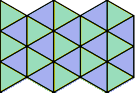 |  |  |  |
|---|---|---|---|
| 3-ти порядък | 4-ти порядък | 5-ти порядък ? | 6-ти порядък |
Положението изглежда безнадежно: правилните петоъгълници имат ъгли 108°. Ако се опитате да наредите плочник с правилни петоъгълници, три не запълват възела до 360°, тъй като 3 х 108° = 324° , а и четири се припокриват, защото 4 х 108° = 432° . Добре, наистина няма други решения, което било ясно още на древните гърци, но какво би станало, ако престъпим лекичко някое от тези ограничения?
Правилните петоъгълници не могат да покрият равнината, но това може да се направи с неправилни петоъгълници.
Търсене на такива петоъгълници е една от най-интересните математически задачи. Търсенето започва през 1918 г., когато математикът Карл Райнхард намира първите пет подходящи фигури.
Дълго време се е вярвало, че Райнхард е намерил всички възможни формули и повече такива петоъгълници не съществуват, но математиците приемат задачата за предизвикателство и през 1985 г те са вече 14.
|
Типове от 1 до 5 са открити от K. Райнхард (K. Reinhardt) през 1918г. B. Кершнер (R. B. Kershner) през 1968г. открива типове от 6 до 8 и заявява, че списъкът е пълен, но през 1975г. Р. Джеймс III (R. James III). пише писмо до Мартин Гарднер, описвайки нов тип - 10. Типовете 9, 11-13 са открити от аматьорката-математик Марджъри Райс (M. Rice) през 1976-1977.Тип 14 е открит от Р. Щайн (R Stein) през 1985. Минете с мишката по номерираните правоъгълници вдясно за да видите досегашните модели правоъгълници, заедно с гормулите им. Илюстрации: wikipedia |
|
|||||||||||||||||||||
Петоъгълници остават единствената фигура, по отношение на която продължава несигурността и мистерията. През 1963 г. е доказано, че има само три вида шестоъгълници, покриващи плътно равнината. Сред изпъкналите седмо-, осмо- и т. н. многоъгълнци, такива няма. Но с петоъгълниците не е съвсем ясно.
Продължение на 30 години, никой не може да намери нещо ново, но най-накрая идва дългоочакваното откритие!
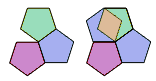
Това направи екип от учени от Университета на Вашингтон: Кейси Ман (Casey Mann), Дженифър Маклауд (Jennifer Mcloud) и Давид вон Деро (David Von Derau).
Ето как изглежда техният елемент:

"Ние открихме фигурата с помощта на компютър с проверка на голям, но ограничен брой варианти - коментира Кейси Ман. - "Разбира се, много сме развълнувани и малко изненадани, че успяхме да открием нов вид петоъгълник".
Търсенето продължава, предизвикателството е интересно.

























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
08.09 2015 в 23:11
14.08 2015 в 19:54
14.08 2015 в 13:51
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон
dolivo
Сахара очаква 75% увеличение на валежите до 2100 г.
dolivo
Земната ябълка: стара култура за новите климатични времена
dolivo
Земята потъмнява. Какво означава тази тревожна климатична тенденция за бъдещето?