
Теорията на игрите има много интересни приложения в икономиката, в биологията (симбиозата, коеволюцията, етологията - взаимоотношенията между организмите и самият естествен отбор) и въобще във всяка ситуация, при която имаме поне две враждуващи (конкурентни) страни с противоположни цели.
Теорията на игрите се занимава с математическите модели за разрешаване на такива ситуации като резултатът от всяко действие на едната страна зависи от начина на действие на конкурентната страна, а всеки от играчите избира различни ходове с цел да максимизира печалбата си.
През 1949 г. Джон Наш пише дисертация на тема теория на игрите, а след 45 години получава Нобелова награда по икономика. Самият Джон Ф. Наш е прототип на героя от филма “Красив ум” (може подробности да прочете тук).
Преди Наш са били разглеждани и анализирани само антагонистични игри, където винаги някой губи, а друг печели за негова сметка. Наш разработва нов метод, наречен равновесието на Наш - оптималната стратегия за игра, включваща двама или повече играчи, като накрая всички играчи постигат взаимна максимална полза, което води до създаване на стабилно равновесие.
Самите играчи имат изгода да поддържат този баланс, тъй като всяка промяна ще влоши положението им.
Например коеволюцията (съвместната еволюция) е един вид състезание, при което на всяка еволюционна стъпка на единия организъм, има отговор от другия. И това не са задължително конкуриращи се страни като примера на коеволюцията на гепарда и антилопата. Усъвършенстването на оръжията на хищника води до усъвършенстване на защитата на жертвата, увличайки се в своеобразна “надпревара във въоръжаването“. Лудата конкуренция на все по-големите скорости е довела в края на краищата до баланс, при който и на двете страни им е физиологично и физически невъзможно да продължат.
В бестселъра си "Себичният ген", Ричард Докинс разглежда няколко модела на поведение, които може да се анализират с методите на теорията на игрите като подчертава, че тук не става въпрос за осъзната стратегия, а за несъзнателни програми на поведение, заложени от гените.
Дилемата на затворника
Една от най-известните задачи от теорията на игрите е "Парадоксът (дилемата) на затворника".
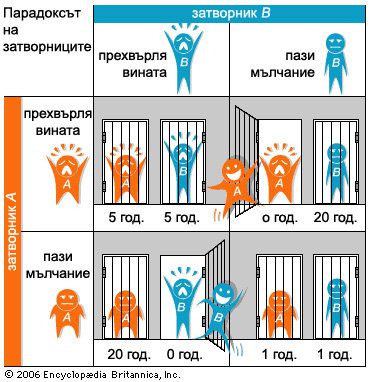 "Двама души – нека ги наречем Питърсън и Мориарти – са в затвора по подозрение в съучастие в престъплението. На всеки от затворниците, в неговата отделна килия, му предлагат да предаде своя приятел, давайки показания в съда срещу него. По-нататъшният ход на събитията зависи от начина, по който ще постъпят двамата затворници, при това, никой не знае как ще постъпи другия. Ако Питърсън стовари вината върху Мориарти, а Мориарти запази мълчание и по този начин той ще потвърди вината си (кооперирайки се със своя бивш и както се оказа, вероломен приятел), тогава Мориарти ще получи една дълга присъда, а Питърсън ще бъде освободен невредим, получавайки Награда за риска. Ако всеки от тях обвиняваше другия, то ще осъдят и двамата за престъплението, вменено им, но и двамата ще получат известна снизходителност за даването на показания и присъдата ще бъде Наказание за взаимно отхвърляне, въпреки че е донякъде смекчена. Ако и двамата престъпници се кооперират (един с друг, а не с властите), и откажат да дадат показания, то доказателствата за вината им може да се окажат недостатъчни за да осъдят който и да е от тях за основното престъпление и ще получат по-малък срок на присъдата за по-дребно престъпление – Награда за взаимно сътрудничество.
"Двама души – нека ги наречем Питърсън и Мориарти – са в затвора по подозрение в съучастие в престъплението. На всеки от затворниците, в неговата отделна килия, му предлагат да предаде своя приятел, давайки показания в съда срещу него. По-нататъшният ход на събитията зависи от начина, по който ще постъпят двамата затворници, при това, никой не знае как ще постъпи другия. Ако Питърсън стовари вината върху Мориарти, а Мориарти запази мълчание и по този начин той ще потвърди вината си (кооперирайки се със своя бивш и както се оказа, вероломен приятел), тогава Мориарти ще получи една дълга присъда, а Питърсън ще бъде освободен невредим, получавайки Награда за риска. Ако всеки от тях обвиняваше другия, то ще осъдят и двамата за престъплението, вменено им, но и двамата ще получат известна снизходителност за даването на показания и присъдата ще бъде Наказание за взаимно отхвърляне, въпреки че е донякъде смекчена. Ако и двамата престъпници се кооперират (един с друг, а не с властите), и откажат да дадат показания, то доказателствата за вината им може да се окажат недостатъчни за да осъдят който и да е от тях за основното престъпление и ще получат по-малък срок на присъдата за по-дребно престъпление – Награда за взаимно сътрудничество.
Ако се поставите на мястото на всеки от затворниците, приемайки че и двамата са движени от разумен егоизъм, и помнейки, че те нямат възможност да говорят помежду си за да се разберат, тогава ще разберете че никой от тях няма друг избор, освен да предаде другия.
Възможно ли е да се разреши този парадокс? И двамата знаят, че независимо от действията на противника, най-доброто нещо, което могат да направят сами е да изберат “Отказвам сътрудничество с конкурента”, но също така знаем, че ако и двамата се Кооперират, всеки от тях би бил в по-добра позиция.
"Ако най-малко един от играчите не се окаже истински светец, а не от този свят, играта неминуемо ще приключи през взаимен отказ с парадоксално мизерен резултат и за двамата играчи." Така излага същността на играта Ричард Докинс.
За да математизираме процеса можем произволно да определим стойност на резултата за отделния играч в точки или пари.
"Налице е “Банкер”, който ще съди играта и изплаща печалби на двамата играчи. Нека допуснем, че играя срещу вас. В ръцете на всеки играч има само по две карти с думите: “Кооперирам се” и “Отказвам”. Всеки от нас избира една от своите две карти и я поставя на масата с лице надолу, така че никой от играчите не знае какво е избрал другия, в действителност, и двамата слагат картите си едновременно. Играчите след това очакват напрегнато Банкерът да обърне картите. Напрежението произтича от факта, че печалбата зависи не само от собствения ход (всеки играч знае каква карта е поставил), но и от хода на противника (който е неизвестен, докато банкерът не обърне картите).
Тъй като играта се играе от 2 x 2 карти, има четири възможни резултати (от уважение към американския произход на играта, наградите са дадени в долари):
Резултат I.
И двамата играем “Кооперирам се”.Банкерът плаща на всеки от нас по $ 300.Тази почтена сума се нарича “награда за взаимно сътрудничество”.
Резултат II.
И двамата играем “Отказвам”. Банкерът глобява всеки от нас с $ 10. Това се нарича “наказание за взаимен отказ”.
Резултат III.
Вие сте играли “Кооперирам се”, а аз “Отказвам”. Банкерът ми плаща $ 500 (Такса за риск) и глобява вас (Наивника) с $ 100.
Резултат IV
Вие играете “Отказвам”, а аз “Кооперирам се”. Банкерът ви плаща за риска от $ 500 и глобява мен (Наивника) с $ 100."
Резултатът можем да обобщим в таблица
| I | II | III | IV | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ход | + | - | ход | + | - | ход | + | - | ход | + | - | |
| A | да | 300 | не | 10 | не | 500 | да | 100 | ||||
| B | да | 300 | не | 10 | да | 100 | не | 500 | ||||
Ясно е, че резултатите от III и IV са огледални образи един на друг, единият играч побеждава, а другият губи. При резултати I и II се оказват наравно, но резултат I е по-изгоден за двамата, отколкото резултат II. Точната сума на печалбата няма значение. Не е важно и колко резултати са положителни (плащания) и колко отрицателни (глоби). Най-важното условие за да се гарантира, че играта е истински Парадокс на затворника е относителния ранг (цена) на резултатите. “Таблицата на ранговете” трябва да е следната:
- Награда за риска.
- Награда за взаимно сътрудничество,
- Наказание за взаимен отказ.
- Наказание за Наивника.
Строго погледнато, има още едно условие, спазването на което е необходимо за признаването на играта за Парадокс на затворника, средната стойност между Наградата за риска и Глобата за Наивника да не надвишава Наградите.
В какво се състои “парадокса”? За да разберем това, опитайте да си представите мислите, преминаващи през главата ми, когато играя срещу вас. Знам, че има само две карти, от които може да изберете: “Кооперирам се” или “Отказвам”. Нека да ги обсъдим една по една. Ако изберете: “Отказвам” (това означава, че ние трябва да погледнем към дясната страна на матрицата), тогава най-доброто нещо, което мога да направя, е да играя “Отказвам" . Вярно е, че ще се наложи да се плати глоба за взаимен отказ, но ако аз избера: “Кооперирам се”, щях да съм глобен като Наивник, което е по-лошо. Сега да се обърнем към лявата половина на матрицата, т.е. нека кажем, че вие сте избрали картата “Кооперирам се” . Отново е по-добре да играя “Отказвам” . Ако бях избрал “Кооперирам се” и двамата щяхме да имаме доста висока печалба – по $ 300. Но ако избера “Отказвам”, ще спечеля още $ 300 отгоре. Стигаме до извода, че независимо коя карта изберете, моята най-добра тактика е винаги да играя “Отказвам”.
И така, по пътя на безупречни логически разсъждения, установих, че независимо от действията ви, трябва да отказвам. С помощта на същата безупречна логика, стигате до същото заключение и вие. По този начин, когато се срещнат двама разумни играчи, те и двамата ще играят “Отказвам” , и двамата в крайна сметка ще заплатят глоби или ще получат малка печалба. В допълнение, всеки от тях знае, че ако двамата играят само “Кооперирам се” , всеки ще получи сравнително по-висока награда за взаимно сътрудничество (в този случай $ 300). Ето защо играта се нарича парадокс.
Многократен Парадокс на затворника
Но има и друга версия на тази игра. Тя се нарича Итериран или Многократен Парадокс на затворника.
Ако играта се повтаря многократно и всеки от затворниците планира следващия си ход, имайки предвид хода на противника си, тогава картината се променя. Такава игра позволява да определим дали можем да се доверим на противника или не, да отвърнем на всеки удар или да се сдобрим, да простим или да отмъстим. В една безкрайно дълга игра е много важно да се уверим, че и двамата печелим от банкера, а не за сметка един на друг.
След десет партии, теоретично бих могъл да спечеля 5 000$, но само ако вие сте изключително глупав (или праведен) и винаги сте играл “Кооперирам се”, въпреки факта, че през цялото време съм играл “Отказвам”. По-реалистично е да се предположи, че всеки от нас ще получи по 3 000 долара от банкера, ако и двамата и 10-те пъти сме играли “Кооперирам се”. Затова ние не трябва да сме особено праведни, защото и двамата можем да се убедим въз основа на предишната игра на противника, че може да му се има доверие. Ние, всъщност, може да регулираме поведението си взаимно. Възможна е също така игра в друга посока: никой от нас да не вярва на другия и двамата да играем “Отказвам” всичките десет пъти и банкерът да получи от всеки от нас по 100 $ под формата на глоби. По-скоро ние частично ще се доверяваме един на друг, всеки ще играе ту “Кооперирам се”, ту “Отказвам” и в резултат ще получим някаква междинна сума пари."
Турнир на Акселрод
Броят на стратегиите, възможни в итеративната игра е ограничен единствено от нашата изобретателност. Възможно ли е да се определи коя от тях е най-добрата? Тази задача е поставил пред себе си Акселрод. Той имал интересната идея да организира конкурс и поканил експерти по теория на игрите, за да представят своите стратегии. В този случай, стратегиите са предварително разработени програми за действие и съответно, конкурентите са представили своите заявки на програмен език. Предложени са били четиринадесет стратегии. Акселрод добавил петнадесета, наричайки я Случайна, при която просто се играе без никаква система ту “Кооперирам се”, ту “Отказвам” и служи като един вид базова “анти-стратегия”: стратегията, даваща по-лоши резултати от Случайната, следва да се признае за много лоша.
Тук не ни интересува коя именно стратегия е излязла победител в играта срещу всеки отделен противник. За нас е важно да се определи коя стратегия печели най-много “пари” за всичките 15 варианта. “Парите” са просто “точки” разпределени, както следва:
- за взаимно Коопериране – 3 точки;
- за Риск – 5 точки;
- Наказание за взаимен отказ – 1 точка (в еквивалент на малката глоба в играта, описана по-рано),
- Глоба за Наивника – 0 точки (еквивалент на голямата глоба в играта, описана по-рано).
Максималната възможна печалба, която може да получи при една или друга стратегия, е 15 000 точки (200 партиди от пет точки средно на мач всяка от 15-те противника). Минималният резултат е 0. Излишно е да се казва, че нито един от тези крайни резултати не се случва. Най-голямата печалба, на която може реално да се надява дадена стратегия средно за 15-те турнира, не може значително да надвишава 600 точки. Това е всичко, което може да получи всеки един от двамата играчи, ако те и двамата играят през цялото време “Кооперирам се”, печелейки по 3 точки за всяка от 200-те изиграни игри. Ако един от тях се поддаде на изкушението да се откаже, броя на точките, вероятно щеше да е по-малък от 600, защото другият играч ще му отвърне със същото (в болшинството от представените стратегии е бил заложен в една или друга форма стремеж за ответен удар). Ние можем да използваме числото 600 като един вид база за сравнение за дадена игра и резултатите ще се изразяват като процент от това число. По тази скала теоретично е възможно да се достигне печалба до 166% (1000 точки), но практически ни една от стратегиите не заработва повече от средно 600 точки.
Не забравяйте, че “играчи” в турнира не са хора, а програми, по-точно – програмирани стратегии.
Око за око
Били предложени много хитри стратегии, но излезе, че печелившата стратегия е много проста. Тя се нарича “Око за око” и е била представена от проф. Анатол Рапопорт (Anatol Rapoport), известен психолог и специалист по теория на игрите от Торонто. Според тази стратегия, първият ход трябва да бъде “Кооперирам се”, а по-нататък, просто се повтаря предишния ход на другия играч.
Наивен Изпитател и други тактики
Тук представям един опростен вариант на турнира с добавяне на още няколко любопитни стратегии.
Например стратегия, наречена Наивен Изпитател. Програмата Наивен Изпитател е по същество идентична с програмата Око за око, освен че от време на време, да кажем, веднъж на десет хода, без някаква закономерност безпричинно играе “Отказвам” и взема 5 точки, полагащи му се за риск.
Добавила съм и стратегията "Павлов" - добронамерена стратегия, която повтаря същия ход, който й е донесъл успех на предишния ход.
Изводите от турнира на Акселрод са, че печелившите стратегии се отличават с добронамереност и умение да прощаваш, макар че в тази симулация ще се уверите, че често печели "случайната" стратегия, т.е. непредвидимостта има предимство.
Теорията на еволюционно стабилните стратегии
Ричард Докинс прилага теорията на игрите в поведението на животните като теория на еволюционно стабилните стратегии (ЕСС).
Разликата е, че една стратегия се смята за ефективна тогава, когато остава ефективна и в среда, доминирана от нейните копия.
В състезанията на Акселрод наборът от предложените стратегии са произволни. Така, по чиста случайност в турнира на Акселрод, около половината стратегии са били добронамерени. При тези обстоятелства, Око за око спечели и Око за две очи щеше да спечели, ако беше участвала в турнира.
Да предположим обаче, че всички стратегии случайно се оказват недобронамерени. Например, ако броят на недобронамерените стратегии е 13 от 15-те, то Око за око нямаше да спечели.
Важна характеристика на една еволюционно стабилна стратегия е, че тя продължава да бъде ефективна, когато е многочислена в дадена популация от стратегии. Ако Око за око е еволюционно стабилна стратегия, това означава, че Око за око е ефективна в ситуация, в която тази стратегия е доминираща.
В света на дарвинизма печалби се изплащат не в пари, а като потомство и успешна стратегия е тази стратегия, която е станала многобройна в дадена популация от стратегии.
 Снимка: Auckland Zoo
Снимка: Auckland Zoo
В популация, в която “Винаги отказвам” вече е постигнал господстващо положение, нито една друга стратегия не може да я победи по ефективност. Ние можем да разглеждаме системата като имаща две точки на стабилност, едната от тях е “Винаги отказвам“, а другата – Око за око (или някаква смес от преобладаваща част добронамерени стратегии). Тази точка на стабилност, която първа заеме доминиращо положение в популацията, тя и остава доминантна.
Много е важно от коя страна на прага ще се окаже дадена популация в самото начало. Дали популацията понякога може да премине от едната страна на прага на другата?
Да предположим, че започваме с популацията, която вече се намира на страната на “Винаги отказвам“. Малкото индивиди, придържащи се към стратегията Око за око, не се срещат достатъчно често, за да си бъдат взаимно изгодни.
Така естественият отбор избутва популацията още повече, до най-крайната точка на “Винаги отказвам“. Ако можеше тази популация просто по някакъв начин, в резултат на случаен дрейф да пресече прага, тя би могла да се хлъзне по склона на страната на стратегията Око за око и за всички щеше да бъде много изгодно и щеше да плаща банкерът или “Природата”.
Завист
Око за око е “добронамерена” стратегия, т.е. никога не отказва първа и е “незлопаметна”, т.е. бързо забравя миналите злодеяния. Акселрод въвежда стратегията: “Око за око независтлива“. Да бъдеш завистлив според Акселрод означава стремеж да се спечелят повече пари от другия играч, а не да се стремиш да получиш повече в абсолютно изражение от капитала на банкера. Да си независтлив означава да се чувстваш напълно удовлетворен, ако другият играч получава точно толкова пари, колкото и вие, при условие, че и двамата да печелите по този начин повече от банкера. Око за око никога истински не “печелят” играта, тя не може да събере повече точки от “противника” във всяка отделна игра, защото отказва само като отмъщение.
Когато психолозите провеждат играта Итериран Парадокс на затворника между реални хора, почти всички играчи се поддават на чувството на завист и затова успехите им са сравнително малки. Изглежда, че много хора, даже без да съзнават това са по-скоро готови да натопят другия играч, отколкото да се кооперират с тях, за да разорят банкера. Цялата заблуда на такава стратегия показва Акселрод.
Игри с нулеви и ненулеви суми
В теорията на игрите има игри с “нулева сума” и с “ненулева сума“. В игрите с нулева сума, при които печели единия играч, това винаги се придружава със загубата на другия. Игра от този тип е шаха, тъй като целта на всеки играч е да спечели, т. е., другият играч да загуби. Обаче парадоксът на затворника е игра с ненулева сума. В него са участва банкера, изплащащ парите и двама играчи, които ако се обединят могат да разорят банката.
В теорията на игрите могат да се дадат различни примери за игри с нулеви и ненулеви суми
Например едно бракоразводно дело вместо игра с ненулева сума (ако двете страни се споразумеят), благодарение на адвокатите се превръща в игра с нулева сума, игра , в която се търси победител и победен. Но за самите адвокати играта е с ненулева сума, особено ако се споразумеят адвокатите на двете страни дружно да се възползват от клиентите си, протакайки делото.
Когато водим преговори за да ни повишат заплатите, дали сме мотивирани от завист или се кооперираме за да максимизираме нашите реалните доходи? Ние вярваме, че в реалния живот, както и в психологическите експерименти, че участваме в игра с нулев резултат, докато в действителност тя не е такава.
Друг интересен пример е футболния мач, който е типична игра с нулева сума, но понякога се случват мачове, в които равенството удовлетворява и двата отбора, т.е играта е с ненулева сума и отборите се “кооперират” и размотават по терена за неудоволствие на зрителите.
Акселрод дава за пример за един интересен феномен по време на Първата световна война за това, колко важна може да бъде сянката на бъдещето. Разказва се за дружестките отношения, които са се установявали на отделни места по фронта. И двете страни са се придържали към политиката “живей и остави другите да живеят.”
Примерите могат да продължат до безкрай. Надявам се, че това бегло изложение е предизвикало любопитството ви и респектът, който заслужава математиката не само като отвлечена абстракция, а и като реално приложение в много аспекти на съществуването.
Източници:
What exactly is 'game theory'?
Себичният ген. Дилемата на затворника – част 12, Ричард Докинс
Себичният ген. Саможертва или егоизъм – част 8, Ричард Докинс
Себичният ген. Симбиоза или експлоатация - част 10, Ричард Докинс
























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон