
Невроучени използваха алгебрична топология по напълно нов начин - да надзърнат в структурата на човешкия мозък. Те са успели да открият, че мозъкът е пълен с многоизмерни геометрични структури, работещи в до 11 измерения, съобщава ScienceAlert.
Резултатите от това ново проучване могат да се окажат следващата голяма стъпка в разбирането на устройството на човешкия мозък - най-сложната структура, която познаваме.
Изследването е проведено от екип учени от Blue Brain Project - швейцарска изследователска инициатива, посветена на изграждането на реконструкция на човешкия мозък, задвижвана от суперкомпютър. Резултатите са публикувани във Frontiers of Computational Neuroscience.
Екипът използва алгебрична топология, разклонение на математиката, използвано за описване на свойствата на обектите и пространствата без значение на това как променят формата си. Учените откриват, че групa неврони се свързват в "клики" (cliques) и че увеличаването на броя на невроните в една клика водят до дименсии в многоизмерен геометричен обект.
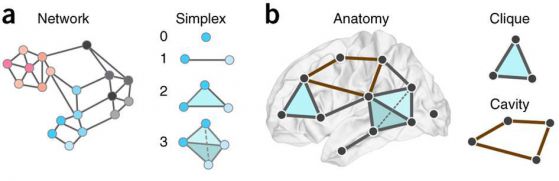 (А) Вляво е традиционният начин, по който да изучават мрежовите системи, включително мозъка, като се проучват модели в двоични отношения между възлите, наречени диади. Диадата традиционно е основна единица в теорията на графите и науката за мрежите. Тук е показан пример мозъчна мрежа, съставена изключително от диади. В много случаи обаче невронните системи проявяват взаимодействия от по-висок ред представени от нулев симплекс (възел), единичен симплекс (линия между два възела), двоен симплекс (запълнен триъгълник) и т.н. (В) Вляво се вижда местоположението на тези симплекси в мозъчна мрежа, от малкия мащаб на невроните до по-големия мащаб на областите на мозъка. Вдясно: клика (всеки с всеки свързани подграфи от всякакъв размер) и кухина (сбор от п симплекса, които са подредени така, че да образуват празна геометрична граница). Източник: Network neuroscience, Danielle S Bassett & Olaf Sporns / Nature Neuroscience, March 2017 Volume 20, No 3
(А) Вляво е традиционният начин, по който да изучават мрежовите системи, включително мозъка, като се проучват модели в двоични отношения между възлите, наречени диади. Диадата традиционно е основна единица в теорията на графите и науката за мрежите. Тук е показан пример мозъчна мрежа, съставена изключително от диади. В много случаи обаче невронните системи проявяват взаимодействия от по-висок ред представени от нулев симплекс (възел), единичен симплекс (линия между два възела), двоен симплекс (запълнен триъгълник) и т.н. (В) Вляво се вижда местоположението на тези симплекси в мозъчна мрежа, от малкия мащаб на невроните до по-големия мащаб на областите на мозъка. Вдясно: клика (всеки с всеки свързани подграфи от всякакъв размер) и кухина (сбор от п симплекса, които са подредени така, че да образуват празна геометрична граница). Източник: Network neuroscience, Danielle S Bassett & Olaf Sporns / Nature Neuroscience, March 2017 Volume 20, No 3
"Открихме един свят, който не сме си и представяли", казва водещият учен Хенри Маркрам (Henry Markram) от института EPFL в Швейцария. "Има десетки милиони от тези обекти дори в едно малко зрънце от мозъка над 7 измерения. В някои мрежи открихме структури с до 11 измерения", допълва той.
Човешкият мозък е изчислено, че разполага с 86 милиарда неврони, в множество връзки от всяка клетка, разклоняващи се във всяка възможна посока, като така формират обширна клетъчна мрежа, която по някакъв начин ни прави способни да мислим и да осъзнаваме.
С подобен огромен брой връзки, с които може да се работи, не е чудно, че все още няма цялостно разбиране по какъв начин действа невронната мрежа на мозъка. Но новата математическа рамка, изградена от екипа от Blue Brain Project, ни приближава една стъпка по-близо до това един ден да разполагаме с дигитален модел на мозъка.
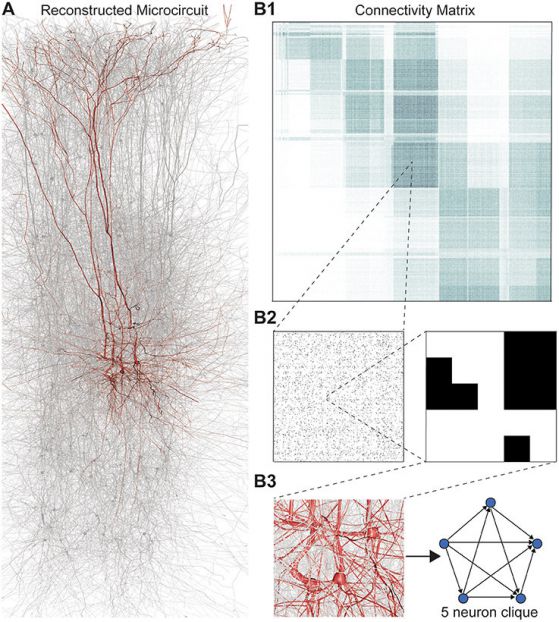
За да изпълни математическите тестове, екипът използва детайлен модел на неокортекса (или нова кора), който е публикуван от същия екип през 2015 г. Смята се, че неокортексът е най-наскоро еволюиралата част от човешкия мозък, тази, която участва в някои от най-сложните функции като познанието и сензорното възприятие.
След като разработва своята математическа рамка и я тества за няколко виртуални стимула, екипът потвърждава получените резултати и върху истинска мозъчна тъкан от плъхове.
Според учените алгебричната топология предоставя математически инструменти за забелязване на подробности от невронната мрежа, както от близка гледна точка на ниво отделни неврони, така и в по-голям размер - структурата на мозъка като цяло.
Като свързват тези две нива, учените успяват да забележат многоизмерни геометрични структури в мозъка, образувани от сбор от плътно свързани неврони (клики) и празни пространства (кухини) между тях.
"Открихме забележително голям брой и разнообразие на многоизмерно насочени клики и кухини, които не са били забелязвани досега в невронните мрежи, нито биологично, нито изкуствено", пише екипът в своето проучване.
"Алгебричната топология е като телескоп и микроскоп едновременно", отбелязва математикът Катрин Хес (Kathryn Hess) от EPFL. "С нея можем да се приближим към мрежите, за да открием скритите структури, дърветата в гората, и да видим празните пространства - всичко това по едно и също време", допълва тя.
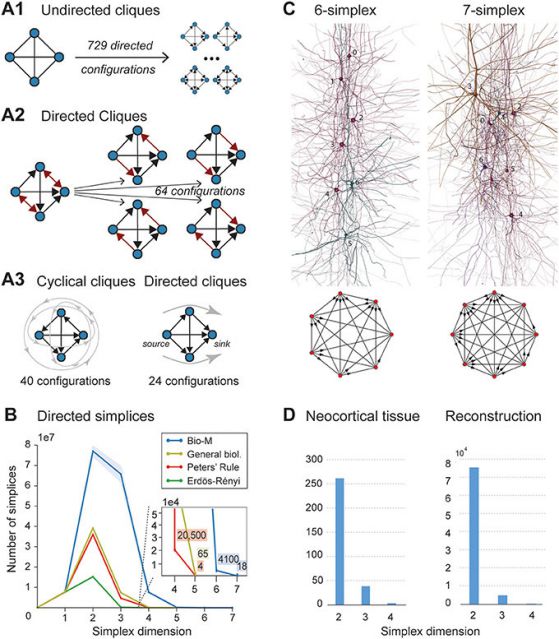
Тези празни пространства или кухини изглеждат от изключително голяма важност за функционирането на мозъка. Когато учените дават стимул на виртуалната мозъчна тъкан, те наблюдават, че невроните реагират на него по един силно организиран начин.
"Това е като мозъкът да реагира на един стимул като изгражда и след това разрушава кула от многоизмерни блокове, като се започне от пръчки (1D), след това дъски (2D), после тухли (3D), и по-сложни геометрии с 4D, 5D и т.н.", коментира математикът Ран Леви (Ran Levi) от Университета в Абърдийн, Шотландия. "Прогресията на активността наподобява многоизмерен пясъчен замък, който се материализира от пясъка и след това се разпада", добавя той.
Откритията на екипа предоставят омагьосваща нова картина на това как мозъкът обработва информацията, но учените отбелязват, че все още не е ясно какво кара кликите и кухините да се образуват по техния силно специфичен начин.
Необходими са допълнителни изследвания за определяне по какъв начин сложността на тези многоизмерни геометрични форми, създадени от човешките неврони, са съизмерими със сложността на различни познавателни задачи.


















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон