

–ü―Ä–Β–Ζ –Ω–Ψ―¹–Μ–Β–¥–Ϋ–Η―²–Β –Ϋ―è–Κ–Ψ–Μ–Κ–Ψ –¥–Ϋ–Η –Ω–Ψ―²―Ä–Β–±–Η―²–Β–Μ–Η―²–Β –Ϋ–Α ―¹–Ψ―Ü–Η–Α–Μ–Ϋ–Η –Φ–Β–¥–Η–Η ―¹–Ω–Ψ–¥–Β–Μ―è―² –Η –≥–Μ–Β–¥–Α―² –Β–¥–Η–Ϋ –Η–Ζ–Κ–Μ―é―΅–Η―²–Β–Μ–Ϋ–Ψ –¥–Ψ–±―Ä–Β –Ϋ–Α–Ω―Ä–Α–≤–Β–Ϋ GIF, –Κ–Ψ–Ι―²–Ψ –¥–Β–Φ–Ψ–Ϋ―¹―²―Ä–Η―Ä–Α –Β–¥–Ϋ–Α –≥–Β–Ϋ–Η–Α–Μ–Ϋ–Α –Η–¥–Β―è.
–ê–Ϋ–Η–Φ–Η―Ä–Α–Ϋ–Ψ―²–Ψ –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Β –Ω–Ψ–Κ–Α–Ζ–≤–Α –≤―ä–Ζ–¥―É―à–Β–Ϋ –Ω–Ψ–≥–Μ–Β–¥ –Ϋ–Α –±―Ä–Β–≥–Ψ–≤–Α –Η–≤–Η―Ü–Α, –¥–Ψ–Κ–Α―²–Ψ –Κ–Α–Φ–Β―Ä–Α―²–Α –±–Α–≤–Ϋ–Ψ ―¹–Β –Ω―Ä–Η–±–Μ–Η–Ε–Α–≤–Α. –ö–Μ–Η–Ω―ä―² –Η–Ζ–≥–Μ–Β–Ε–¥–Α –Ω―Ä–Ψ–¥―ä–Μ–Ε–Η―²–Β–Μ–Β–Ϋ,¬†–Ϋ–Ψ –≤―¹―ä―â–Ϋ–Ψ―¹―²¬†―²―Ä–Α–Β ―¹–Α–Φ–Ψ –¥–≤–Β ―¹–Β–Κ―É–Ϋ–¥–Η.
–½–Α–±–Μ―É–¥–Α―²–Α ―¹–Β –¥―ä–Μ–Ε–Η –Ϋ–Α ―¹–Η–Μ–Α―²–Α –Ϋ–Α ―³―Ä–Α–Κ―²–Α–Μ–Η―²–Β –Η –Ω–Α―Ä–Α–¥–Ψ–Κ―¹–Α –Ϋ–Α –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Μ–Η–Ϋ–Η―è.
–ü–Α―Ä–Α–¥–Ψ–Κ―¹―ä―² –≥–Μ–Α―¹–Η, ―΅–Β –Β―¹―²–Β―¹―²–≤–Β–Ϋ–Ψ―²–Ψ –Κ―Ä–Α–Ι–±―Ä–Β–Ε–Η–Β –Ϋ―è–Φ–Α –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Α –¥―ä–Μ–Ε–Η–Ϋ–Α. –Δ–Ψ–≤–Α –Φ–Ψ–Ε–Β –¥–Α –Η–Ζ–≥–Μ–Β–Ε–¥–Α –Ϋ–Β–≤–Β―Ä–Ψ―è―²–Ϋ–Ψ, –Ϋ–Ψ –Β –≤―è―Ä–Ϋ–Ψ. –î―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α –Κ―Ä–Α–Ι–±―Ä–Β–Ε–Η–Β―²–Ψ –Ζ–Α–≤–Η―¹–Η –Ψ―² "–Α―Ä―à–Η–Ϋ–Α", ―¹ –Κ–Ψ–Ι―²–Ψ ―¹–Β –Φ–Β―Ä–Η.
Please Bring Your Chairs And Tables To The Upright Position
–Γ―²–Α–Ϋ–¥–Α―Ä―²–Β–Ϋ –Ω―Ä–Η–Φ–Β―Ä –Ζ–Α ―²–Ψ–Ζ–Η –Ω–Α―Ä–Α–¥–Ψ–Κ―¹ –Β –Η–Ζ–Φ–Β―Ä–≤–Α–Ϋ–Β―²–Ψ –Ϋ–Α –±―Ä–Η―²–Α–Ϋ―¹–Κ–Ψ―²–Ψ –Κ―Ä–Α–Ι–±―Ä–Β–Ε–Η–Β. –ê–Κ–Ψ ―¹–Β –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α―²–Β –Η–Ζ–Φ–Β―Ä–Η―²–Β–Μ–Ϋ–Α –Β–¥–Η–Ϋ–Η―Ü–Α –Ψ―² 200 –Κ–Φ –Ψ―΅–Β―Ä―²–Α–Ϋ–Η–Β―²–Ψ –Ϋ–Α –±―Ä–Η―²–Α–Ϋ―¹–Κ–Η―è –Ψ―¹―²―Ä–Ψ–≤ ―â–Β –Β 2400 –Κ–Φ, –Α–Κ–Ψ –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α―²–Β 100-–Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Ψ–≤ –Α―Ä―à–Η–Ϋ - 2 800 –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α. –ù–Ψ –Α–Κ–Ψ –Ω―Ä–Β–Φ–Β―Ä–Η–Φ –±―Ä–Η―²–Α–Ϋ―¹–Κ–Ψ―²–Ψ –Κ―Ä–Α–Ι–±―Ä–Β–Ε–Η–Β ―¹ –Ω–Ψ–Φ–Ψ―â―²–Α –Ϋ–Α –Μ–Η–Ϋ–Η―è ―¹ –¥―ä–Μ–Ε–Η–Ϋ–Α –Ψ―² 50 –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α, –£–Β–Μ–Η–Κ–Ψ–±―Ä–Η―²–Α–Ϋ–Η―è ―â–Β ―¹–Ω–Β―΅–Β–Μ–Η –Ψ–Κ–Ψ–Μ–Ψ 600 –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α –Ω–Ψ–≤–Β―΅–Β –Ψ―² –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Μ–Η–Ϋ–Η―è, –¥–Ψ―¹―²–Η–≥–Α–Ι–Κ–Η –Ψ–±―â–Ψ 3400 –Κ–Η–Μ–Ψ–Φ–Β―²―Ä–Α. –ê –Α–Κ–Ψ –Η–Ζ–Φ–Β―Ä–≤–Α–Φ–Β ―¹ –Μ–Η–Ϋ–Η–Ι–Κ–Α –Ψ―² –Β–¥–Η–Ϋ –Φ–Η–Κ―Ä–Ψ–Ϋ?
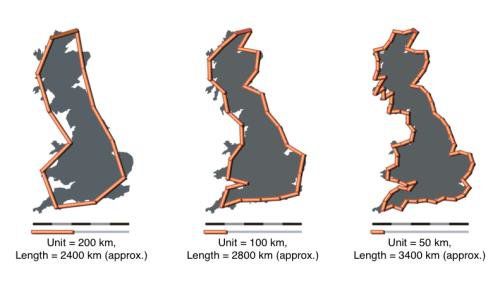
–½–Α―â–Ψ ―¹–Β –Ω–Ψ–Μ―É―΅–Α–≤–Α ―²–Α–Κ–Α? –ü―Ä–Ψ–±–Μ–Β–Φ―ä―² –Β, ―΅–Β ―¹–Β –Ψ–Ω–Η―²–≤–Α–Φ–Β –¥–Α –Η–Ζ–Φ–Β―Ä–Η–Φ –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Μ–Η–Ϋ–Η―è –Κ–Α―²–Ψ –Κ–≤–Α–¥―Ä–Α―² –Η–Μ–Η –Φ–Ϋ–Ψ–≥–Ψ―ä–≥―ä–Μ–Ϋ–Η–Κ, –Ϋ–Ψ –Ϋ–Β –Φ–Ψ–Ε–Β–Φ –¥–Α ―è –Η–Ζ–Φ–Β―Ä–Η–Φ ―²–Ψ―΅–Ϋ–Ψ –Ω–Ψ ―²–Ψ–Ζ–Η –Φ–Α―΅–Η–Ϋ - –≤–≥–Μ–Β–¥–Α–Ι―²–Β ―¹–Β –≤ ―¹–Ϋ–Η–Φ–Κ–Α―²–Α –Ϋ–Α–Ι-–≥–Ψ―Ä–Β - –Κ–Ψ–Μ–Κ–Ψ―²–Ψ –Ω–Ψ–≤–Β―΅–Β ―¹–Β –Ω―Ä–Η–±–Μ–Η–Ε–Α–≤–Α–Φ–Β, ―²–Ψ–Μ–Κ–Ψ–≤–Α –Ω–Ψ–≤–Β―΅–Β ―¹–Β ―É–≤–Β–Μ–Η―΅–Α–≤–Α―² –¥–Β―²–Α–Ι–Μ–Η―²–Β.
–Δ–Ψ–≤–Α –Β ―¹–≤―ä―Ä–Ζ–Α–Ϋ–Ψ ―¹ –Β–¥–Ϋ–Α –Ζ–Α–±–Α–≤–Ϋ–Α –≥–Β–Ψ–Ω–Ψ–Μ–Η―²–Η―΅–Β―¹–Κ–Α –Η–¥–Β―è.
–ü–Ψ –≤―Ä–Β–Φ–Β –Ϋ–Α¬†–£―²–Ψ―Ä–Α―²–Α ―¹–≤–Β―²–Ψ–≤–Ϋ–Α –≤–Ψ–Ι–Ϋ–Α –Α–Ϋ–≥–Μ–Η–Ι―¹–Κ–Η―è―² –Φ–Α―²–Β–Φ–Α―²–Η–Κ –¦―é–Η―¹ –Λ―Ä–Α–Ι –†–Η―΅–Α―Ä–¥―¹―ä–Ϋ –±–Η–Μ –Ψ―¹–Β–Ϋ–Β–Ϋ –Ψ―² –Ψ―Ä–Η–≥–Η–Ϋ–Α–Μ–Ϋ–Α –Η–¥–Β―è. –Δ–Ψ–Ι –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Η–Μ, ―΅–Β –Α–≥―Ä–Β―¹–Η–≤–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α –Β–¥–Ϋ–Α –¥―ä―Ä–Ε–Α–≤–Α –Η–Μ–Η –Η–Φ–Ω–Β―Ä–Η―è –Ζ–Α–≤–Η―¹–Η –Ψ―² –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α –Ϋ–Β–Ι–Ϋ–Α―²–Α –≥―Ä–Α–Ϋ–Η―Ü–Α. –Γ–Ω–Ψ―Ä–Β–¥ –Ϋ–Β–≥–Ψ –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ―¹―²―²–Α –Ζ–Α –≤–Ψ–Ι–Ϋ–Α –Φ–Β–Ε–¥―É –¥–≤–Β ―¹―ä―¹–Β–¥–Ϋ–Η –¥―ä―Ä–Ε–Α–≤–Η –Ζ–Α–≤–Η―¹–Η –Ψ―² –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α –≥―Ä–Α–Ϋ–Η―Ü–Α―²–Α, –Κ–Ψ―è―²–Ψ –≥–Η ―Ä–Α–Ζ–¥–Β–Μ―è. –½–Α–Ω–Ψ―΅–Ϋ–Α–Μ –¥–Α ―¹―ä–±–Η―Ä–Α –¥–Α–Ϋ–Ϋ–Η, –Ϋ–Ψ ―¹–Β –Ϋ–Α―²―ä–Κ–Ϋ–Α–Μ –Ϋ–Α –Ω–Α―Ä–Α–¥–Ψ–Κ―¹–Α, ―΅–Β –≤ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Η―²–Β ―¹–Ω―Ä–Α–≤–Ψ―΅–Ϋ–Η―Ü–Η –¥―ä–Μ–Ε–Η–Ϋ–Η―²–Β –Ϋ–Α –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Μ–Η–Ϋ–Η―è –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä –Ϋ–Α –ê–Ϋ–≥–Μ–Η―è ―¹–Β ―Ä–Α–Ζ–Μ–Η―΅–Α–≤–Α–Μ–Α ―¹ 20-30%, –¥–Ψ―Ä–Η –Η 2 –Ω―ä―²–Η. –½–Α―²–Ψ–≤–Α –†–Η―΅–Α―Ä–¥―¹―ä–Ϋ ―Ä–Β―à–Η–Μ –¥–Α –Η–Ζ–Φ–Β―Ä–Η ―¹–Α–Φ –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α –±―Ä–Β–≥–Α –Ϋ–Α –ê–Ϋ–≥–Μ–Η―è. –ù–Ψ ―¹–Κ–Ψ―Ä–Ψ ―Ä–Α–Ζ–±―Ä–Α–Μ, ―΅–Β –Κ–Ψ–Μ–Κ–Ψ―²–Ψ –Ω–Ψ-–Ω–Ψ–¥―Ä–Ψ–±–Ϋ–Η –Κ–Α―Ä―²–Η –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Μ, ―²–Ψ–Μ–Κ–Ψ–≤–Α –Ω–Ψ-–¥―ä–Μ–≥–Α ―¹―²–Α–≤–Α–Μ–Α –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Α―²–Α –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Μ–Η–Ϋ–Η―è.
–†–Η―΅–Α―Ä–¥―¹―ä–Ϋ ―É―¹―²–Α–Ϋ–Ψ–≤–Η–Μ, ―΅–Β –Ϋ–Α―Ä–Α―¹―²–≤–Α–Ϋ–Β―²–Ψ ―¹―²–Α–≤–Α –Ω–Ψ –¥–Ψ–±―Ä–Β –Η–Ζ―Ä–Α–Ζ–Β–Ϋ ―¹―²–Β–Ω–Β–Ϋ–Β–Ϋ –Ζ–Α–Κ–Ψ–Ϋ. –Δ–Ψ–Ι –Β ―¹―ä–Ω–Ψ―¹―²–Α–≤–Η–Μ ―¹―²―ä–Ω–Κ–Α―²–Α –Ϋ–Α –Η–Ζ–Φ–Β―Ä–≤–Α–Ϋ–Β –Η –Ω–Ψ–Μ―É―΅–Β–Ϋ–Α―²–Α –¥―ä–Μ–Ε–Η–Ϋ–Α –Η –Ϋ–Α–Φ–Β―Ä–Η–Μ –¥–Ψ–±―Ä–Β –Η–Ζ―Ä–Α–Ζ–Β–Ϋ–Η –Μ–Η–Ϋ–Β–Ι–Ϋ–Η –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―²–Η –≤ –Μ–Ψ–≥–Α―Ä–Η―²–Φ–Η―΅–Ϋ–Η –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²–Η. –‰–Ζ―Ä–Α–Ζ–Β–Ϋ–Η –≥―Ä–Α―³–Η―΅–Ϋ–Ψ, ―²–Β―Ö–Ϋ–Η―è―² –Ϋ–Α–Κ–Μ–Ψ–Ϋ –±–Η–Μ –Φ―è―Ä–Κ–Α –Ζ–Α ―²–Ψ–≤–Α –Κ–Ψ–Μ–Κ–Ψ –Β –Β―Ä–Ψ–Ζ–Η―Ä–Α–Μ (–Ϋ–Α―¹–Β―΅–Β–Ϋ, –Ϋ–Α–Ζ―ä–±–Β–Ϋ) –±―Ä–Β–≥–Α.

–ê–Κ–Ψ –Ϋ―è–Κ–Ψ–Ι ―Ä–Β―à–Η –¥–Α –Ω―Ä–Ψ–¥―ä–Μ–Ε–Η ―É–Ω–Ψ―Ä–Η―²–Ψ –Ζ–Α–¥–Α―΅–Α―²–Α –Ϋ–Α –†–Η―΅–Α―Ä–¥―¹―ä–Ϋ –Η –Ψ―²–Η–¥–Β –Ϋ–Α –Φ―è―¹―²–Ψ, –≤ –ê–Ϋ–≥–Μ–Η―è –Η ―¹ –¥―ä―Ä–≤–Ψ–¥–Β–Μ―¹–Κ–Η –Φ–Β―²―ä―Ä –Η–Ζ–Φ–Β―Ä–Η –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Ι –Μ–Η–Ϋ–Η―è, ―²–Α–Ζ–Η –¥―ä–Μ–Ε–Η–Ϋ–Α ―â–Β –±―ä–¥–Β –Ψ―â–Β –Ω–Ψ-–≥–Ψ–Μ―è–Φ–Α –Ψ―² –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―²–Β –Ω–Ψ –Κ–Α―Ä―²–Α. –€–Ψ–Ε–Β –¥–Α ―¹–Β –Ω―Ä–Ψ–¥―ä–Μ–Ε–Η ―²–Ψ–Ζ–Η –Ω―Ä–Ψ―Ü–Β―¹ –Ψ―â–Β, –¥–Ψ–Κ–Α―²–Ψ ―¹ –Ω–Ψ–¥―Ö–Ψ–¥―è―â ―É―Ä–Β–¥ –Ϋ–Β ―¹–Β ―¹―²–Η–≥–Ϋ–Β –¥–Ψ –Ω–Β―¹―ä―΅–Η–Ϋ–Κ–Η―²–Β, –¥–Ψ –Α―²–Ψ–Φ–Η―²–Β –Η–Μ–Η –¥–Ψ –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α –ü–Μ–Α–Ϋ–Κ. –½–Α–¥–Α―΅–Α―²–Α –Β –Ϋ–Β–Ω–Ψ―¹–Η–Μ–Ϋ–Α.
–ö―Ä–Α–Ι–±―Ä–Β–Ε–Η–Β―²–Ψ –Φ–Ψ–Ε–Β –Ϋ–Α–Ι-–¥–Ψ–±―Ä–Β –¥–Α ―¹–Β –Α–Ω―Ä–Ψ–Κ―¹–Η–Φ–Η―Ä–Α –Κ–Α―²–Ψ ―³―Ä–Α–Κ―²–Α–Μ, ―¹–Ω–Β―Ü–Η–Α–Μ–Ϋ–Α –≥–Β–Ψ–Φ–Β―²―Ä–Η―΅–Ϋ–Α –Κ―Ä–Η–≤–Α, ―΅–Η―è―²–Ψ ―¹–Μ–Ψ–Ε–Ϋ–Ψ―¹―² ―¹–Β –Ω―Ä–Ψ–Φ–Β–Ϋ―è ―¹ –Η–Ζ–Φ–Β―Ä–≤–Α―²–Β–Μ–Ϋ–Α―²–Α ―¹–Κ–Α–Μ–Α.¬†
–Δ–Β―Ä–Φ–Η–Ϋ―ä―² "―³―Ä–Α–Κ―²–Α–Μ" –Β ―¹―ä–Ζ–¥–Α–¥–Β–Ϋ –Ψ―² –ë–Β–Ϋ–Ψ–Α –€–Α–Ϋ–¥–Β–Μ–±―Ä–Ψ―². –Κ–Ψ–Ι―²–Ψ –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α ―²–Ψ–Ζ–Η –Ω―Ä–Η–Φ–Β―Ä –Ζ–Α –¥–Α –Ω–Ψ–Κ–Α–Ε–Β, ―΅–Β –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Μ–Η–Ϋ–Η―è –Ϋ–Α –ê–Ϋ–≥–Μ–Η―è –Η–Φ–Α –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Α –¥―ä–Μ–Ε–Η–Ϋ–Α¬†–Η –≤―¹―ä―â–Ϋ–Ψ―¹―² –Β ―³―Ä–Α–Κ―²–Α–Μ, –Κ–Ψ–Ι―²–Ψ –Η–Φ–Α –¥―Ä–Ψ–±–Ϋ–Α ―Ä–Α–Ζ–Φ–Β―Ä–Ϋ–Ψ―¹―². (–≤–Ε "–Γ–Κ―Ä–Η―²–Η―²–Β –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è –Ϋ–Α ―³―Ä–Α–Κ―²–Α–Μ–Ϋ–Α―²–Α ―Ä–Α–Ζ–Φ–Β―Ä–Ϋ–Ψ―¹―²")
–£ ―¹–Μ―É―΅–Α―è ―¹ –Α–Ϋ–Φ–Η―Ä–Α–Ϋ–Η―è GIF¬†–Β –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Ϋ–Ψ, –Ζ–Α –¥–Α –≤–Η –Ζ–Α–±–Μ―É–¥–Η, –Β–¥–Ϋ–Ψ –¥―Ä―É–≥–Ψ ―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Ϋ–Α ―³―Ä–Α–Κ―²–Α–Μ–Η―²–Β - ―¹–Α–Φ–Ψ–Ω–Ψ–¥–Ψ–±–Ϋ–Ψ―¹―².
–™–Β–Ψ–Φ–Β―²―Ä–Η―΅–Ϋ–Η―²–Β ―³―Ä–Α–Κ―²–Α–Μ–Η ―¹–Α –Η–¥–Β–Ϋ―²–Η―΅–Ϋ–Η –≤―ä–≤ –≤―¹–Η―΅–Κ–Η ―¹–Κ–Α–Μ–Η, –Κ–Ψ–Β―²–Ψ –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α, ―΅–Β –Α–Κ–Ψ –Ω―Ä–Η–±–Μ–Η–Ε–Α–≤–Α―²–Β –Κ―ä–Φ –Ϋ―è–Κ–Ψ―è ―΅–Α―¹―² –Ψ―² ―³–Η–≥―É―Ä–Α―²–Α, ―â–Β –≤–Η–¥–Η―²–Β, ―΅–Β –Β–¥–Ϋ–Α –Η ―¹―ä―â–Α ―¹―²―Ä―É–Κ―²―É―Ä–Α, –Κ–Ψ―è―²–Ψ ―¹–Β –Ω–Ψ–≤―²–Α―Ä―è –Ψ―²–Ϋ–Ψ–≤–Ψ –Η –Ψ―²–Ϋ–Ψ–≤–Ψ.
 –Δ–Ψ–≤–Α –Β –Α–Ϋ–Η–Φ–Α―Ü–Η―è, –¥–Β–Φ–Ψ–Ϋ―¹―²―Ä–Η―Ä–Α―â–Α ―¹–Α–Φ–Ψ–Ω–Ψ–¥–Ψ–±–Η–Β―²–Ψ –Η –Ϋ–Α ―²―Ä–Η–Φ–Β―Ä–Ϋ–Η―è ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η (―²–Β―²―Ä–Α–Β–¥―ä―Ä) –Ϋ–Α –Γ–Β―Ä–Ω–Η–Ϋ―¹–Κ–Η
–Δ–Ψ–≤–Α –Β –Α–Ϋ–Η–Φ–Α―Ü–Η―è, –¥–Β–Φ–Ψ–Ϋ―¹―²―Ä–Η―Ä–Α―â–Α ―¹–Α–Φ–Ψ–Ω–Ψ–¥–Ψ–±–Η–Β―²–Ψ –Η –Ϋ–Α ―²―Ä–Η–Φ–Β―Ä–Ϋ–Η―è ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η (―²–Β―²―Ä–Α–Β–¥―ä―Ä) –Ϋ–Α –Γ–Β―Ä–Ω–Η–Ϋ―¹–Κ–Η

–£―ä–Ω―Ä–Β–Κ–Η ―΅–Β ―³―Ä–Α–Κ―²–Α–Μ–Η―²–Β –Η–Φ–Η―²–Η―Ä–Α―² –Ω―Ä–Η―Ä–Ψ–¥–Ϋ–Η –Ψ–±–Β–Κ―²–Η, –Κ–Α―²–Ψ –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä –±―Ä–Β–≥–Ψ–≤–Α―²–Α –Η–≤–Η―Ü–Α, –¥―ä―Ä–≤–Β―²–Α, –Ψ–±–Μ–Α―Ü–Η, –Ω–Μ–Α–Ϋ–Η–Ϋ–Η (–Κ–Α–Φ―ä–Ϋ–Η), ―Ö–Ψ―Ä–Α―²–Α –Ϋ–Β –Φ–Ψ–≥–Α―² –Μ–Β―¹–Ϋ–Ψ –¥–Α ―Ä–Α–Ζ–Ω–Ψ–Ζ–Ϋ–Α–≤–Α―² ―¹–Α–Φ–Ψ–Ω–Ψ–¥–Ψ–±–Ϋ–Η―²–Β –Φ–Ψ–¥–Β–Μ–Η. –Δ–Ψ–≤–Α ―¹–Α –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Μ–Η –Η ―¹―ä–Ζ–¥–Α―²–Β–Μ–Η―²–Β –Ϋ–Α¬†GIF-–Α.
–û―â–Β –Ω–Ψ ―²–Β–Φ–Α―²–Α

–€–Α―²–Β–Φ–Α―²–Η–Κ–Α
–†–Α―¹―²–Β–Ϋ–Η―è―²–Α - ―³―Ä–Α–Κ―²–Α–Μ–Ϋ–Η―è―² –Α–Μ–≥–Ψ―Ä–Η―²―ä–Φ –Ϋ–Α –±–Ψ―²–Α–Ϋ–Η–Κ–Α―²–Α

–€–Α―²–Β–Φ–Α―²–Η–Κ–Α
–ê–Μ–≥–Β–±―Ä–Η―΅–Ϋ–Η (–¥–Η–Ϋ–Α–Φ–Η―΅–Ϋ–Η, –Ϋ–Β–Μ–Η–Ϋ–Β–Ι–Ϋ–Η) ―³―Ä–Α–Κ―²–Α–Μ–Η
–€–Α―²–Β–Φ–Α―²–Η–Κ–Α
–Γ–Α–Φ–Ψ–Ω–Ψ–¥–Ψ–±–Η–Β





















–ö–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
–€–Ψ–Μ―è, ―Ä–Β–≥–Η―¹―²―Ä–Η―Ä–Α–Ι―²–Β ―¹–Β –Ψ―² T–Θ–ö!
–ê–Κ–Ψ –≤–Β―΅–Β –Η–Φ–Α―²–Β ―Ä–Β–≥–Η―¹―²―Ä–Α―Ü–Η―è, –Ϋ–Α―²–Η―¹–Ϋ–Β―²–Β –Δ–Θ–ö!
–ù―è–Φ–Α –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η –Κ―ä–Φ ―²–Α–Ζ–Η –Ϋ–Ψ–≤–Η–Ϋ–Α !
–ü–Ψ―¹–Μ–Β–¥–Ϋ–Η –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
YKoshev
–î–Ψ–Κ–Ψ–Μ–Κ–Ψ ―¹―ä–≤–Φ–Β―¹―²–Η–Φ–Η ―¹–Α –Φ–Η–Ϋ–Β―Ä–Α–Μ–Ϋ–Ψ-―¹―É―Ä–Ψ–≤–Η–Ϋ–Ϋ–Η―è―² –Ψ―²―Ä–Α―¹―ä–Μ –Η ―΅–Η―¹―²–Α―²–Α –Ψ–Κ–Ψ–Μ–Ϋ–Α ―¹―Ä–Β–¥–Α?
–ö–Ψ–Ζ–Ψ–Ϋ
–€–Η―¹―²–Β―Ä–Η–Ψ–Ζ–Β–Ϋ ―΅–Β―Ä–Β–Ω –Ϋ–Α –≥―Ä―ä―Ü–Κ–Η ―Ö–Ψ–Φ–Η–Ϋ–Η–Ϋ –Β –¥–Α―²–Η―Ä–Α–Ϋ –Ϋ–Α –Ω–Ψ–Ϋ–Β 286 000 –≥–Ψ–¥–Η–Ϋ–Η
Peter Petrov
–Γ–Μ–Β–¥ –Φ–Ϋ–Ψ–≥–Ψ–Κ―Ä–Α―²–Ϋ–Η –Β–Κ―¹–Ω–Μ–Ψ–Ζ–Η–Η –Ϋ–Ψ–≤ ―²–Β―¹―² –Ζ–Α –Φ–Β–≥–Α―Ä–Α–Κ–Β―²–Α―²–Α –Ϋ–Α –€―ä―¹–Κ
–Ω–Ψ–Ω –î―Ä―ä–≤―΅–Ψ
–™–Μ–Β–¥–Α–Ι―²–Β –Ζ–Α –Ω―ä―Ä–≤–Η –Ω―ä―² –Ϋ–Α –Ε–Η–≤–Ψ –Κ–Α–Κ –Ϋ–Ψ–≤–Ψ–Ψ―²–Κ―Ä–Η―²–Η―è―² "–Φ–Β–Ε–¥―É–Ζ–≤–Β–Ζ–¥–Β–Ϋ –Ω–Ψ―¹–Β―²–Η―²–Β–Μ" 3I/ATLAS ―¹–Β ―É―¹―²―Ä–Β–Φ―è–≤–Α –Κ―ä–Φ –Ϋ–Α―¹