

–° –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –Ĺ–ĺ–≤–ł –ł–∑—á–ł—Ā–Ľ–ł—ā–Ķ–Ľ–Ĺ–ł –ľ–Ķ—ā–ĺ–ī–ł —É—á–Ķ–Ĺ–ł—ā–Ķ —Ā–į —É—Ā–Ņ–Ķ–Ľ–ł –ī–į –ĺ—ā–ļ—Ä–ł—Ź—ā —Ā—ā–ĺ—ā–ł—Ü–ł –Ņ—ä—ā–ł –Ņ–ĺ–≤–Ķ—á–Ķ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–ł –ĺ—Ä–Ī–ł—ā–ł, –ĺ—ā–ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ī—Ź—Ö–į –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł –Ņ—Ä–Ķ–ī–ł —ā–ĺ–≤–į,¬†–Ĺ–į –Ņ–ĺ–∑–Ĺ–į—ā–į—ā–į –ĺ—Č–Ķ –ĺ—ā –≤—Ä–Ķ–ľ–Ķ—ā–ĺ –Ĺ–į –Ě—é—ā–ĺ–Ĺ –∑–į–ī–į—á–į –Ĺ–į —ā—Ä–ł—ā–Ķ —ā–Ķ–Ľ–į, —Ā—ä–ĺ–Ī—Č–ł phys.org.
–í—Ā–ł—á–ļ–ł —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź —Ā–į –Ĺ–į–ľ–Ķ—Ä–Ķ–Ĺ–ł –∑–į –ī–≤—É–ľ–Ķ—Ä–Ĺ–ł—Ź —Ā–Ľ—É—á–į–Ļ —Ā –Ĺ—É–Ľ–Ķ–≤ –Ĺ–į—á–į–Ľ–Ķ–Ĺ —ä–≥–Ľ–ĺ–≤ –ľ–ĺ–ľ–Ķ–Ĺ—ā, –ļ–ĺ–Ķ—ā–ĺ –ĺ—ā–Ĺ–ĺ–≤–ĺ –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–į —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—ā–į –ī–ĺ—Ä–ł –Ņ—Ä–ł –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–į —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–ĺ–≤–ļ–į –Ĺ–į –∑–į–ī–į—á–į—ā–į.
–ē–ļ–ł–Ņ—ä—ā –ļ–ł—ā–į–Ļ—Ā–ļ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł—ā–Ķ —Ā–ł –≤ –ī–≤–Ķ —Ā—ā–į—ā–ł–ł, –Ķ–ī–Ĺ–į—ā–į –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–į –≤ —Ā–Ņ–ł—Ā–į–Ĺ–ł–Ķ Science China-Physics Mechanics Astronomy, –į –≤—ā–ĺ—Ä–į—ā–į - –Ĺ–į —Ā—ä—Ä–≤—ä—Ä–į¬†–∑–į –Ņ—Ä–Ķ–ī–Ņ–Ķ—á–į—ā arXiv.org.
–°—ä—Č–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –∑–į–ī–į—á–į—ā–į –Ĺ–į —ā—Ä–ł—ā–Ķ —ā–Ķ–Ľ–į¬†–Ķ –ī–į —Ā–Ķ –ĺ—ā–ļ—Ä–ł–Ķ –ļ–į–ļ —ā—Ä–ł —ā–Ķ–Ľ–į —Č–Ķ —Ā–Ķ –ī–≤–ł–∂–į—ā –Ķ–ī–Ĺ–ĺ —Ā–Ņ—Ä—Ź–ľ–ĺ –ī—Ä—É–≥–ĺ, –≤–∑–į–ł–ľ–ĺ–ī–Ķ–Ļ—Ā—ā–≤–į–Ļ–ļ–ł —Ā–ł —Ā–Ņ–ĺ—Ä–Ķ–ī –∑–į–ļ–ĺ–Ĺ–į –∑–į¬†–≥—Ä–į–≤–ł—ā–į—Ü–ł—Ź—ā–į –Ĺ–į –Ě—é—ā–ĺ–Ĺ, –ļ–ĺ–Ļ—ā–嬆—Ź —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į –ĺ—Č–Ķ –Ņ—Ä–Ķ–∑ 1687 –≥. –≤ "–ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ł –Ĺ–į –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–į—ā–į —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą–ł—Ź". –í —Ā–Ľ—É—á–į—Ź –Ĺ–į –ī–≤–Ķ —ā–Ķ–Ľ–į, –ĺ–Ī—Č–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –Ķ –ī–ĺ–Ī—Ä–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ĺ - —ā–ĺ –Ķ –ĺ—ā–ļ—Ä–ł—ā–ĺ –ĺ—ā –ô–ĺ—Ö–į–Ĺ –ö–Ķ–Ņ–Ľ–Ķ—Ä. –Ě–ĺ –∑–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł —ā–Ķ–Ľ–į —Ā–Ķ –ĺ–ļ–į–∑–į –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-—ā—Ä—É–ī–Ĺ–į. –° –Ĺ–Ķ—Ź —Ā–į —Ā–Ķ –∑–į–Ĺ–ł–ľ–į–≤–į–Ľ–ł –ľ–Ĺ–ĺ–≥–ĺ –≤–Ķ–Ľ–ł–ļ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł –ł —Ą–ł–∑–ł—Ü–ł –ļ–į—ā–ĺ –õ–į–≥—Ä–į–Ĺ–∂, –ě–Ļ–Ľ–Ķ—Ä, –•–į–ľ–ł–Ľ—ā—ä–Ĺ>, –ü–ĺ–į–Ĺ–ļ–į—Ä–Ķ, –í–į–Ļ–Ķ—Ä—Č—Ä–į—Ā –ł –ī—Ä.
–ó–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł—ā–Ķ —ā–Ķ–Ľ–į¬†–ĺ–Ņ–ł—Ā–≤–į¬†–ī–≤–ł–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —á–į—Ā—ā–ł—Ü–ł—ā–Ķ –Ņ–ĺ–ī –≤–Ľ–ł—Ź–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ī–≤–į —Ü–Ķ–Ĺ—ā—ä—Ä–į, –ļ–ĺ–ł—ā–ĺ –Ņ—Ä–ł–≤–Ľ–ł—á–į—ā —á–į—Ā—ā–ł—Ü–į—ā–į —Ā —Ü–Ķ–Ĺ—ā—Ä–į–Ľ–Ĺ–ł —Ā–ł–Ľ–ł, –ļ–ĺ–ł—ā–ĺ –Ĺ–į–ľ–į–Ľ—Ź–≤–į—ā —Ā —É–≤–Ķ–Ľ–ł—á–į–≤–į–Ĺ–Ķ –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ —Ā –ļ–≤–į–ī—Ä–į—ā–į –Ĺ–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ. –ü—Ä–ł–ľ–Ķ—Ä–ł –∑–į –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —ā–į–∑–ł –∑–į–ī–į—á–į –Ķ –Ņ–Ľ–į–Ĺ–Ķ—ā–į, –ī–≤–ł–∂–Ķ—Č–į —Ā–Ķ –≤ –≥—Ä–į–≤–ł—ā–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ—ā–ĺ –Ņ–ĺ–Ľ–Ķ –Ĺ–į –ī–≤–Ķ –∑–≤–Ķ–∑–ī–ł –ł–Ľ–ł –Ķ–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ –≤ –Ķ–Ľ–Ķ–ļ—ā—Ä–ł—á–Ķ—Ā–ļ–ĺ—ā–ĺ –Ņ–ĺ–Ľ–Ķ –Ĺ–į –ī–≤–Ķ —Ź–ī—Ä–į.
–ü—ä—Ä–≤–ł—ā–Ķ —ā—Ä–ł —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź —Ā–į –Ĺ–į–ľ–Ķ—Ä–Ķ–Ĺ–ł –ĺ—ā –õ–Ķ–ĺ–Ĺ–į—Ä–ī –ě–Ļ–Ľ–Ķ—Ä –Ņ—Ä–Ķ–∑ 1767 –≥., –ļ–ĺ–≥–į—ā–ĺ –≤—Ā–ł—á–ļ–ł—ā–Ķ —ā—Ä–ł —ā–Ķ–Ľ–į —Ā–į –Ĺ–į –Ķ–ī–Ĺ–į –Ņ—Ä–į–≤–į. –ü—Ä–Ķ–∑ 1887 –≥. –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ—ä—ā –ź–Ĺ—Ä–ł –ü–ĺ–į–Ĺ–ļ–į—Ä–Ķ –Ņ–ĺ–ļ–į–∑–≤–į, —á–Ķ –Ĺ–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –ĺ–Ī—Č–ĺ –į–Ĺ–į–Ľ–ł—ā–ł—á–Ĺ–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ –∑–į –∑–į–ī–į—á–į—ā–į —Ā —ā—Ä–ł —ā–Ķ–Ľ–į —Ā –į–Ľ–≥–Ķ–Ī—Ä–ł—á–Ĺ–ł –ł–∑—Ä–į–∑–ł –ł –ł–Ĺ—ā–Ķ–≥—Ä–į–Ľ–ł.
–ė–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–ł—Ź—ā–į –≤—ä—Ä—Ö—É –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į –ī–ĺ–≤–Ķ–ī–ĺ—Ö–į –ī–ĺ –ĺ—ā–ļ—Ä–ł–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā.–Ĺ–į—Ä. —á—É–≤—Ā—ā–≤–ł—ā–Ķ–Ľ–Ĺ–į –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā –Ĺ–į—á–į–Ľ–Ĺ–ł—ā–Ķ —É—Ā–Ľ–ĺ–≤–ł—Ź¬†(sensitivity dependence of initial condition - SDIC)¬†–≤ —Ö–į–ĺ—ā–ł—á–Ĺ–ł –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ł. –Ē–Ĺ–Ķ—Ā –Ĺ–į —Ö–į–ĺ—ā–ł—á–Ĺ–į—ā–į –ī–ł–Ĺ–į–ľ–ł–ļ–į —Ā–Ķ –≥–Ľ–Ķ–ī–į –ļ–į—ā–ĺ –Ĺ–į —ā—Ä–Ķ—ā–į—ā–į –≤–Ķ–Ľ–ł–ļ–į –Ĺ–į—É—á–Ĺ–į —Ä–Ķ–≤–ĺ–Ľ—é—Ü–ł—Ź –≤—ä–≤ —Ą–ł–∑–ł–ļ–į—ā–į –Ņ—Ä–Ķ–∑ 20-—ā–ł –≤–Ķ–ļ, —Ā—Ä–į–≤–Ĺ–ł–ľ–į —Ā —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā—ā–į –ł –ļ–≤–į–Ĺ—ā–ĺ–≤–į—ā–į –ľ–Ķ—Ö–į–Ĺ–ł–ļ–į. –ü–ĺ —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–ł—Ź—ā–į –≤—ä—ė֗ɬ†–∑–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł—ā–Ķ —ā–Ķ–Ľ–į –ł–ľ–į –ľ–Ĺ–ĺ–≥–ĺ –≤–į–∂–Ĺ–ĺ –Ĺ–į—É—á–Ĺ–ĺ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ.
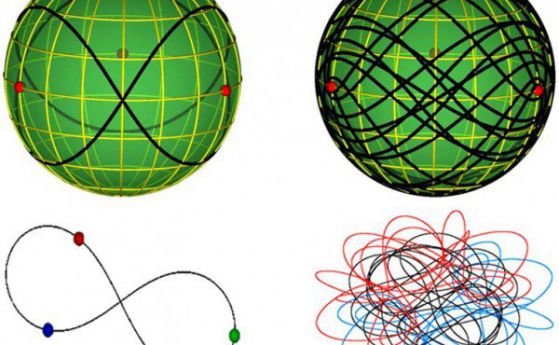
–ü—Ä–Ķ–∑ 1890 –≥. –ü–ĺ–į–Ĺ–ļ–į—Ä–Ķ —É—Ā—ā–į–Ĺ–ĺ–≤–ł, —á–Ķ —ā—Ä–į–Ķ–ļ—ā–ĺ—Ä–ł–ł—ā–Ķ –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–ł —Ā —ā—Ä–ł —ā–Ķ–Ľ–į —á–Ķ—Ā—ā–ĺ —Ā–į –Ĺ–Ķ–Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ĺ–ł, —ā.–Ķ. –ī–į –Ĺ–Ķ —Ā–Ķ –Ņ–ĺ–≤—ā–į—Ä—Ź—ā. –Ę–ĺ–≤–į –ľ–ĺ–∂–Ķ –ī–į –ĺ–Ī—Ź—Ā–Ĺ–ł –∑–į—Č–ĺ –Ķ —ā–ĺ–Ľ–ļ–ĺ–≤–į —ā—Ä—É–ī–Ĺ–ĺ –ī–į —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į—ā –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ĺ–ł –ĺ—Ä–Ī–ł—ā–ł –Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–ł —Ā —ā—Ä–ł —ā–Ķ–Ľ–į.¬†–ó–į –Ĺ–į–ī 300 –≥–ĺ–ī–ł–Ĺ–ł –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–ł—Ź¬†—Ā–į¬†–Ĺ–į–ľ–Ķ—Ä–Ķ–Ĺ–ł —Ā–į–ľ–ĺ —ā—Ä–ł —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į¬† –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ĺ–ł –ĺ—Ä–Ī–ł—ā–ł. –ü—Ä–Ķ–∑ 2013 –≥. –ú–ł–Ľ–ĺ–≤–į–Ĺ –®—É–≤–į–ļ–ĺ–≤ (Milovan ҆uvakov) –ł –í–Ķ–Ľ–ļ–ĺ –Ē–ľ–ł—ā—Ä–į—ą–ł–Ĺ–ĺ–≤–ł—á (Veljko DmitraŇ°inovińá) –ĺ—ā –ė–Ĺ—Ā—ā–ł—ā—É—ā–į –Ņ–ĺ —Ą–ł–∑–ł–ļ–į –≤ –Ď–Ķ–Ľ–≥—Ä–į–ī –Ņ—Ä–į–≤—Ź—ā –Ņ—Ä–ĺ–Ī–ł–≤, –ĺ—ā–ļ—Ä–ł–≤–į–Ļ–ļ–ł 13 –Ĺ–ĺ–≤–ł —Ä–į–∑–Ľ–ł—á–Ĺ–ł –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ĺ–ł –ĺ—Ä–Ī–ł—ā–ł, –ļ–ĺ–ł—ā–ĺ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—ā –Ĺ–į 11 –Ĺ–ĺ–≤–ł —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ĺ—ā –Ě—é—ā–ĺ–Ĺ–ĺ–≤–į—ā–į –∑–į–ī–į—á–į —Ā —ā—Ä–ł —ā–Ķ–Ľ–į —Ā –Ķ–ī–Ĺ–į–ļ–≤–į –ľ–į—Ā–į –ł –Ĺ—É–Ľ–Ķ–≤ —ä–≥–Ľ–ĺ–≤ –ł–ľ–Ņ—É–Ľ—Ā –≤ —Ā–Ľ—É—á–į—Ź –Ĺ–į —Ä–į–≤–Ĺ–ł–Ĺ–į [Phys. Rev. Lett. 110, 114301 (2013)].

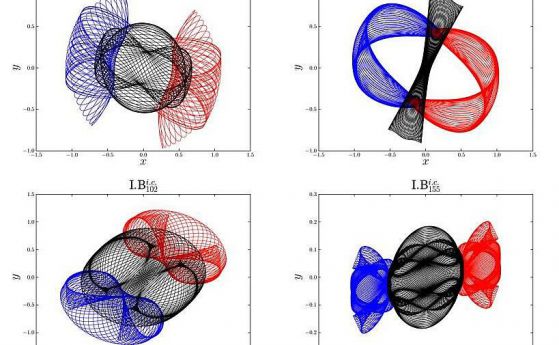
 –°—Ö–Ķ–ľ–į—ā–ł—á–Ĺ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź–Ĺ–Ķ –Ĺ–į —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–ł –ĺ—Ä–Ī–ł—ā–ł –Ĺ–į —ā—Ä–ł —ā–Ķ–Ľ–į. Science China Press
–°—Ö–Ķ–ľ–į—ā–ł—á–Ĺ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź–Ĺ–Ķ –Ĺ–į —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–ł –ĺ—Ä–Ī–ł—ā–ł –Ĺ–į —ā—Ä–ł —ā–Ķ–Ľ–į. Science China Press
–í –Ņ—ä—Ä–≤–į—ā–į –ĺ—ā –ī–≤–Ķ—ā–Ķ –Ĺ–ĺ–≤–ł —Ä–į–Ī–ĺ—ā–ł –Ĺ–į –ļ–ł—ā–į–Ļ—Ā–ļ–ł—ā–Ķ —É—á–Ķ–Ĺ–ł –ö—Ā–ł–į–ĺ–Ĺ–ł–Ĺ–≥ –õ–ł (XiaoMing Li) –ł –®–ł–ī–∑–ł –õ—Ź–ĺ (ShiJun Liao) –ĺ—ā –®–į–Ĺ—Ö–į–Ļ—Ā–ļ–ł—Ź¬† —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –Ē–∂–į–ĺ –Ę–ĺ–Ĺ–≥, –ö–ł—ā–į–Ļ, —É—Ā–Ņ–Ķ—ą–Ĺ–ĺ —Ā–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–Ľ–ł 695 —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –Ņ–Ķ—Ä–ł–ĺ–ī–ł—á–Ĺ–ł –ĺ—Ä–Ī–ł—ā–ł –Ĺ–į –Ķ–ī–Ĺ–į –ł —Ā—ä—Č–į –Ě—é—ā–ĺ–Ĺ–ĺ–≤–į—ā–į —Ä–į–≤–Ĺ–ł–Ĺ–Ĺ–į —Ā–ł—Ā—ā–Ķ–ľ–į —Ā —ā—Ä–ł —ā–Ķ–Ľ–į —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į —Ā—É–Ņ–Ķ—Ä–ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–į TH-2 –≤ –ď—É–į–Ĺ–ī–∂–ĺ—É, –ö–ł—ā–į–Ļ. –ú–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā –Ĺ–ĺ–≤ –ľ–Ķ—ā–ĺ–ī, –Ĺ–į—Ä–Ķ—á–Ķ–Ŭ†—á–ł—Ā—ā–į —á–ł—Ā–Ľ–Ķ–Ĺ–į —Ā–ł–ľ—É–Ľ–į—Ü–ł—Ź (clean numerical simulation - CNS), –ļ–ĺ–Ļ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –Ĺ–į–ľ–į–Ľ–ł –≥—Ä–Ķ—ą–ļ–ł—ā–Ķ.
–í—ä–≤ –≤—ā–ĺ—Ä–į—ā–į —Ä–į–Ī–ĺ—ā–į –Ķ —Ä–į–∑–≥–Ľ–Ķ–ī–į–Ĺ–į –∑–į–ī–į—á–į—ā–į –∑–į —ā—Ä–ł —ā–Ķ–Ľ–į —Ā —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ľ–į—Ā–ł. –í —Ä–Ķ–∑—É–Ľ—ā–į—ā –Ĺ–į —ā–ĺ–≤–į —Ā–į –Ĺ–į–ľ–Ķ—Ä–Ķ–Ĺ–ł 1349 —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ĺ—Ä–Ī–ł—ā–ł, –ĺ—ā –ļ–ĺ–ł—ā–ĺ 1223 —Ā–į –Ĺ–ĺ–≤–ł.
–ú–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –ĺ—ā–Ī–Ķ–Ľ—Ź–∑–≤–į—ā –ļ—Ä–į—Ā–ĺ—ā–į—ā–į –ł –Ķ–Ľ–Ķ–≥–į–Ĺ—ā–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –≥—Ä–į—Ą–ł—á–Ĺ–ĺ—ā–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź–Ĺ–Ķ –Ĺ–į –Ĺ–ĺ–≤–ł—ā–Ķ –ĺ—Ä–Ī–ł—ā–ł: "–Ě–ł–Ķ —Ā–ľ–Ķ –ł–∑—É–ľ–Ķ–Ĺ–ł –ł –ĺ—á–į—Ä–ĺ–≤–į–Ĺ–ł –ĺ—ā —ā—Ź—Ö–Ĺ–ĺ—ā–ĺ –≤–Ķ–Ľ–ł–ļ–ĺ–Ľ–Ķ–Ņ–ł–Ķ". –Ę–Ķ —Ā—ä—Č–ĺ —ā–į–ļ–į –Ņ–ĺ—Ā–ĺ—á–≤–į—ā, —á–Ķ –Ĺ–į–Ņ—Ä–Ķ–ī—ä–ļ—ä—ā —Ā–Ķ –ī—ä–Ľ–∂–ł –≥–Ľ–į–≤–Ĺ–ĺ –Ĺ–į —Ä–į–∑–≤–ł—ā–ł–Ķ—ā–ĺ –Ĺ–į —á–ł—Ā–Ľ–Ķ–Ĺ–ł—ā–Ķ –ľ–Ķ—ā–ĺ–ī–ł, –Ĺ–į –Ĺ–ĺ–≤–ł —Ā—ā—Ä–į—ā–Ķ–≥–ł–ł –∑–į –ľ–ĺ–ī–Ķ–Ľ–ł—Ä–į–Ĺ–Ķ –Ĺ–į —Ö–į–ĺ—ā–ł—á–Ĺ–ł—ā–Ķ –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ł –ł –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —Ā—É–Ņ–Ķ—Ä–ļ–ĺ–ľ–Ņ—é—ā—Ä–ł.


















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
dolivo
–ó–Ķ–ľ–Ĺ–į—ā–į —Ź–Ī—ä–Ľ–ļ–į: —Ā—ā–į—Ä–į –ļ—É–Ľ—ā—É—Ä–į –∑–į –Ĺ–ĺ–≤–ł—ā–Ķ –ļ–Ľ–ł–ľ–į—ā–ł—á–Ĺ–ł –≤—Ä–Ķ–ľ–Ķ–Ĺ–į
dolivo
–ó–Ķ–ľ—Ź—ā–į –Ņ–ĺ—ā—ä–ľ–Ĺ—Ź–≤–į. –ö–į–ļ–≤–ĺ –ĺ–∑–Ĺ–į—á–į–≤–į —ā–į–∑–ł —ā—Ä–Ķ–≤–ĺ–∂–Ĺ–į –ļ–Ľ–ł–ľ–į—ā–ł—á–Ĺ–į —ā–Ķ–Ĺ–ī–Ķ–Ĺ—Ü–ł—Ź –∑–į –Ī—ä–ī–Ķ—Č–Ķ—ā–ĺ?
Nikor
–Ě–į 30 —Ā–Ķ–Ņ—ā–Ķ–ľ–≤—Ä–ł 1928 –Ķ –ĺ—ā–ļ—Ä–ł—ā –Ņ–Ķ–Ĺ–ł—Ü–ł–Ľ–ł–Ĺ—ä—ā
–ü—Ä–ĺ—Ā—ā –ß–ĺ–≤–Ķ–ļ
–Ě–ĺ–≤–ĺ –ĺ–Ī—Ź—Ā–Ĺ–Ķ–Ĺ–ł–Ķ –∑–į –≥–ł–≥–į–Ĺ—ā—Ā–ļ–ł—ā–Ķ –Ķ–ļ—Ā–Ņ–Ľ–ĺ–ī–ł—Ä–į—Č–ł –ļ—Ä–į—ā–Ķ—Ä–ł –≤ –°–ł–Ī–ł—Ä