

–Ь—Г–Ј–µ—П—В –љ–∞ –љ–∞—Г–Ї–∞—В–∞ –Є –Є–љ–і—Г—Б—В—А–Є—П—В–∞ –≤ –Ь–∞–љ—З–µ—Б—В—К—А –≤ —З–µ—Б—В –љ–∞ –≥–µ–љ–Є–∞–ї–љ–Є—П –±—А–Є—В–∞–љ—Б–Ї–Є –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Р–ї—К–љ –Ґ—О—А–Є–љ–≥ –њ—А–µ–і—Б—В–∞–≤–Є –µ–і–Є–љ –Љ–∞—Й–∞–±–µ–љ –≥—А–∞–ґ–і–∞–љ—Б–Ї–Є –њ—А–Њ–µ–Ї—В, —З–Є—П—В–Њ —Ж–µ–ї –µ –і–∞ —А–∞–Ј–Ї—А–Є–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞ —В–∞–є–љ–∞ –љ–∞ –њ—А–Њ—П–≤–∞—В–∞ –љ–∞ —А–µ–і–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є –≤ —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є—В–µ.¬†
–†–µ–Ј—Г–ї—В–∞—В–Є—В–µ –Њ—В –љ–∞—Г—З–љ–Є—П –µ–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В —Б–∞ –њ—Г–±–ї–Є–Ї—Г–≤–∞–љ–Є –≤ –Є–Ј–і–∞–љ–Є–µ—В–Њ –љ–∞¬†–Ъ—А–∞–ї—Б–Ї–Њ—В–Њ –Њ–±—Й–µ—Б—В–≤–Њ¬†Open Science.
–У–Є–≥–∞–љ—В—Б–Ї–Є—В–µ —Ж–≤–µ—В–Њ–≤–µ –љ–∞ —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є—В–µ —Б–∞ –њ—А–µ–Ї—А–∞—Б–љ–∞ –Є –Њ—З–µ–≤–Є–і–љ–∞ –і–µ–Љ–Њ–љ—Б—В—А–∞—Ж–Є—П –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—В–µ –њ—А–∞–≤–Є–ї–∞, –њ–Њ –Ї–Њ–Є—В–Њ —Б–µ —А–∞–Ј–≤–Є–≤–∞ –ґ–Є–≤–Њ—В—К—В. –Ґ–Њ–≤–∞ –µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—П—В —А–µ–і –љ–∞ –§–Є–±–Њ–љ–∞—З–Є, –≤ –Ї–Њ–є—В–Њ –≤—Б—П–Ї–Њ —Б–ї–µ–і–≤–∞—Й–Њ —З–Є—Б–ї–Њ –µ —Б–±–Њ—А –Њ—В –њ—А–µ–і—Е–Њ–і–љ–Є—В–µ –і–≤–µ (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 ..).

|
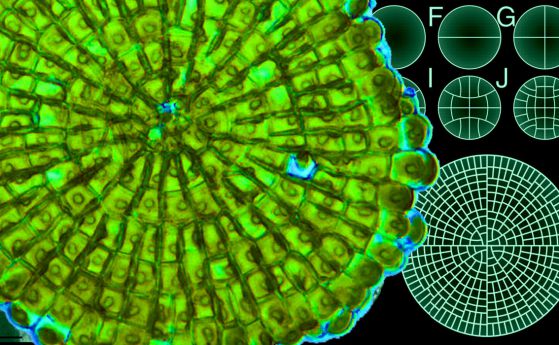
¬†–Х–і–љ–∞ –Њ—В –љ–∞–є-–≤–њ–µ—З–∞—В–ї—П–≤–∞—Й–Є—В–µ –њ—А–Њ—П–≤–Є –љ–∞ —З–Є—Б–ї–∞—В–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є –µ —Б–њ–Є—А–∞–ї–љ–Њ—В–Њ –њ–Њ–і—А–µ–ґ–і–∞–љ–µ –љ–∞ —Б–µ–Љ–µ–љ–∞—В–∞ –≤—К—А—Е—Г –њ–Є—В–∞—В–∞ –љ–∞ —Б–ї—К–љ—З–Њ–≥–ї–µ–і–∞ –Є –љ–∞ –љ—П–Ї–Њ–Є –і—А—Г–≥–Є –Њ—В —Б–µ–Љ–µ–є—Б—В–≤–Њ—В–Њ –љ–∞ –∞—Б—В—А–Є—В–µ. –Ъ–∞–Ї—В–Њ —Б–µ –≤–Є–ґ–і–∞ –љ–∞ —Б–љ–Є–Љ–Ї–∞—В–∞ –≤–ї—П–≤–Њ, —В–∞–Љ —Б–µ –Њ–±—А–∞–Ј—Г–≤–∞—В –і–≤–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –Њ—В –ї–Њ–≥–∞—А–Є—В–Љ–Є—З–љ–Є —Б–њ–Є—А–∞–ї–Є:
—З–µ—А–≤–µ–љ–Є—В–µ —Б–∞ –Њ—А–Є–µ–љ—В–Є—А–∞–љ–Є –њ–Њ –њ–Њ—Б–Њ–Ї–∞ –љ–∞ —З–∞—Б–Њ–≤–љ–Є–Ї–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ –Є —Б–∞ 21. —Б–Є–љ–Є—В–µ —Б–∞ –Њ–±—А–∞—В–љ–Њ –љ–∞ —З–∞—Б–Њ–≤–љ–Є–Ї–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ –Є —Б–∞ 13. –С—А–Њ—П—В –љ–∞ —Б–њ–Є—А–∞–ї–Є—В–µ –≤ –і–≤–µ—В–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –µ —А–∞–Ј–ї–Є—З–µ–љ –Є –њ—А–Њ—П–≤—П–≤–∞ —В–µ–љ–і–µ–љ—Ж–Є—П—В–∞ –і–∞ –Њ–±—А–∞–Ј—Г–≤–∞ –і–≤–Њ–є–Ї–∞ —Б—К—Б–µ–і–љ–Є —З–Є—Б–ї–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є. –°—А–µ–і–љ–Њ –≥–Њ–ї–µ–Љ–Є—В–µ —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ –Є–Љ–∞—В –њ–Њ 34 –Є 55 —Б–њ–Є—А–∞–ї–Є, –љ–Њ —Б–µ —Б—А–µ—Й–∞—В –Є –≥–Є–≥–∞–љ—В—Б–Ї–Є —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є —Б –њ–Њ 89 –Є 144 —Б–њ–Є—А–∞–ї–Є. |

–Р–Ї–Њ —Б–µ –њ—А–µ–±—А–Њ—П—В —Б–њ–Є—А–∞–ї–Є—В–µ –Њ—В —Б–µ–Љ–Ї–Є –≤ —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є, —А–∞–Ј–њ–Њ–ї–Њ–ґ–µ–љ–Є –њ–Њ –Є –Њ–±—А–∞—В–љ–Њ –љ–∞ —З–∞—Б–Њ–≤–љ–Є–Ї–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ —Й–µ –њ–Њ–ї—Г—З–Є–Љ –і–≤–µ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Є —З–Є—Б–ї–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є, –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ 34 –Є 55 –Є–ї–Є 55 –Є 89, –љ–Њ —Б–µ —Б—А–µ—Й–∞—В –Є –≥–Є–≥–∞–љ—В—Б–Ї–Є —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є —Б –њ–Њ 89 –Є 144 —Б–њ–Є—А–∞–ї–Є.
–У–µ–љ–Є–∞–ї–љ–Є—П—В –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Р–ї—К–љ –Ґ—О—А–Є–љ–≥ –µ –±–Є–ї –і—К–ї–±–Њ–Ї–Њ –Ј–∞–Є–љ—В—А–Є–≥—Г–≤–∞–љ –Њ—В –њ—А–Њ—П–≤–∞—В–∞ –љ–∞ —А–µ–і–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є –≤ –њ—А–Є—А–Њ–і–∞—В–∞, —В—К—А—Б–µ–є–Ї–Є –њ—А–Є–Љ–µ—А–Є –Ј–∞ —В–Њ–Ј–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Љ–Њ–і–µ–ї –≤ —Б—В—К–±–ї–∞, –ї–Є—Б—В–∞ –Є —Б–µ–Љ–µ–љ–∞ –Њ—В —А–∞—Б—В–µ–љ–Є—П, –Є–Ј–≤–µ—Б—В–љ–Є –Ї–∞—В–Њ —Д–Є–ї–Њ—В–∞—Е–Є—П¬†(phyllotaxis).
–Р–ї—К–љ –Ґ—О—А–Є–љ–≥¬†—Б—В–∞–≤–∞ –µ–і–Є–љ –Њ—В –њ–Њ—А–µ–і–Є—Ж–∞—В–∞ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є –Є —Г—З–µ–љ–Є, –Ї–Њ–Є—В–Њ —Б–µ –Њ–њ–Є—В–≤–∞—В –і–∞ –Њ–±—П—Б–љ—П—В –њ–Њ–і—А–µ–і–±–∞—В–∞ –њ–Њ –§–Є–±–Њ–љ–∞—З–Є –≤ –њ—А–Є—А–Њ–і–∞—В–∞.
 |
–Ч–∞ –Љ–љ–Њ–≥–Њ —Е–Њ—А–∞ –Њ–±–Њ–±—Й–µ–љ–Є–µ—В–Њ, —З–µ —А–∞—Б—В–µ–љ–Є—П—В–∞ –ґ–Є–≤–µ—П—В –њ–Њ –Ј–∞–Ї–Њ–љ–∞ –љ–∞ —З–Є—Б–ї–Њ–≤–∞—В–∞ —А–µ–і–Є—Ж–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є, –Љ–Њ–ґ–µ –і–∞ —Б–µ —Б—В–Њ—А–Є –њ—А–µ—Б–Є–ї–µ–љ–Њ, –љ–Њ —Й–µ —Б–µ —Б—К–≥–ї–∞—Б–Є—В–µ, —З–µ –≤—Б–µ –њ–∞–Ї –Є–Љ–∞ –љ—П–Ї–∞–Ї–≤–∞ –Ј–∞–≥–∞–і–Ї–∞. –Т –±–Њ—В–∞–љ–Є–Ї–∞—В–∞ —Б—К—Й–µ—Б—В–≤—Г–≤–∞ –і—П–ї, –Ї–Њ–є—В–Њ —Б–µ –љ–∞—А–Є—З–∞ —Д–Є–ї–Њ—В–∞—Е–Є—П –Є –Є–Ј—Г—З–∞–≤–∞ –Ј–∞–Ї–Њ–љ–Њ–Љ–µ—А–љ–Њ—Б—В–Є—В–µ –≤ –њ–Њ–і—А–µ–ґ–і–∞–љ–µ—В–Њ –љ–∞ –ї–Є—Б—В–∞—В–∞.
–Я—А–µ–Ј 1754 –≥. –®–∞—А–ї –С–Њ–љ–µ, –Є–Ј—Г—З–∞–≤–∞–є–Ї–Є —А–∞–Ј–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ—В–Њ –љ–∞ –ї–Є—Б—В–∞—В–∞ –љ–∞ —Б—В—К–±–ї–∞—В–∞ –љ–∞ –љ—П–Ї–Њ–Є —А–∞—Б—В–µ–љ–Є—П, –Њ—В–Ї—А–Є–ї —З–µ –∞–Ї–Њ –Љ–Є—Б–ї–µ–љ–Њ —Б–µ —Б—К–µ–і–Є–љ–Є —Б –ї–Є–љ–Є—П –Љ–µ—Б—В–∞—В–∞ –љ–∞ вАЬ–њ—А–Є–Ї—А–µ–њ–≤–∞–љ–µвАЭ –љ–∞ –ї–Є—Б—В–∞—В–∞, —В–Њ —Й–µ —Б–µ –њ–Њ–ї—Г—З–∞—В –љ—П–Ї–Њ–ї–Ї–Њ —Б–њ–Є—А–∞–ї–Є, –Є–ї–Є —В. –љ. –≥–µ–љ–µ—В–Є—З–µ–љ –≤–Є–љ—В вАУ –≥–µ–љ–µ—В–Є—З–µ–љ, –Ј–∞—Й–Њ—В–Њ —А–∞–Ј–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ—В–Њ –љ–∞ –ї–Є—Б—В–∞—В–∞ –Њ—В–≥–Њ–≤–∞—А—П –љ–∞ —А–µ–і–∞ –Є–Љ –љ–∞ –њ–Њ—П–≤–∞ –Њ—В–і–Њ–ї—Г –љ–∞–≥–Њ—А–µ. –Ю–Ї–∞–Ј–∞–ї–Њ —Б–µ, —З–µ —А–∞–Ј—Б—В–Њ—П–љ–Є–µ—В–Њ –Љ–µ–ґ–і—Г —Ж–Є–Ї–ї–Є—В–µ –љ–∞ –ї–Є—Б—В–∞—В–∞ —Б–∞ –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї–љ–Є –љ–∞ —З–Є—Б–ї–∞—В–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є –Є–ї–Є a/b=b/c=~1.6. –Ґ–Њ–≤–∞ —Б–µ –љ–∞–±–ї—О–і–∞–≤–∞ –Љ–љ–Њ–≥–Њ –і–Њ–±—А–µ –њ—А–Є —Ж–Є–Ї–Њ—А–Є—П—В–∞. –Ы–Є—Б—В–∞—В–∞ –љ–µ –Є–Ј—А–∞—Б—В–≤–∞—В –њ—А–Њ–Є–Ј–≤–Њ–ї–љ–Њ –љ–∞ —Б—В—К–±–ї–Њ—В–Њ: —В–µ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В —А–∞–Ј–њ–Њ–ї–Њ–ґ–µ–љ–Є –Ї–∞–Ї—В–Њ –∞–ї—В–µ—А–љ–∞—В–Є–≤–љ–Њ (–њ—А–µ–Ј –µ–і–љ–Њ), —В–∞–Ї–∞ –Є –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Њ –љ–∞ 2 —А–µ–і–∞, –Є–ї–Є –њ–Њ —Б–њ–Є—А–∞–ї–∞. –Ы–Є—Б—В–∞—В–∞, –Ї–Њ–Є—В–Њ –Љ–Њ–≥–∞—В –і–∞ —Б–µ –≥—А—Г–њ–Є—А–∞—В –≤ –µ–і–љ–∞ —Б–њ–Є—А–∞–ї–∞ —Б–µ –љ–∞—А–Є—З–∞—В –њ–∞—А–∞—Б—В–Є—Е. |
 –Э–∞ —Б—Е–µ–Љ–∞—В–∞ –≤–і—П—Б–љ–Њ –µ –Є–Ј–Њ–±—А–∞–Ј–µ–љ–Њ —А–∞—Б—В–µ–љ–Є–µ—В–Њ Protea cynaroides –Є –Љ–Њ–ґ–µ –і–∞ —Б–µ –Ј–∞–±–µ–ї–µ–ґ–Є, —З–µ –≤—Б–µ–Ї–Є –Њ—Б–Љ–Є –ї–Є—Б—В –Ј–∞–µ–Љ–∞ —Б—К—Й–∞—В–∞ –≤–µ—А—В–Є–Ї–∞–ї–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П –Ї–∞—В–Њ –њ—К—А–≤–Є—П –ї–Є—Б—В –љ–∞ —Б—В—К–±–ї–Њ—В–Њ (0). –Ю—Б–≤–µ–љ —В–Њ–≤–∞, –≤—Б–µ–Ї–Є –Њ—Б–Љ–Є –ї–Є—Б—В –Є–і–≤–∞ —В–Њ—З–љ–Њ —Б–ї–µ–і —В—А–Є –Њ–±–Њ—А–Њ—В–∞ –Є–ї–Є 3 —Ж–Є–Ї—К–ї–∞ (–Њ–±–Њ—А–Њ—В–Є) –Ј–∞ –њ–µ—А–Є–Њ–і. –Р–Ї–Њ –±—А–Њ—П –љ–∞ –ї–Є—Б—В–∞—В–∞ –Ј–∞ –њ–µ—А–Є–Њ–і –µ n, –∞ –±—А–Њ—П –љ–∞ –Њ–±–Њ—А–Њ—В–Є—В–µ –Ј–∞ –њ–µ—А–Є–Њ–і вАУ m, —В–Њ P. cynaroides –Є–Љ–∞ m = 3 –Є n = 8: –і–≤–µ —З–Є—Б–ї–∞ –Њ—В –њ–Њ–Ј–љ–∞—В–∞—В–∞ –љ–Є —А–µ–і–Є—Ж–∞!
–Э–∞ —Б—Е–µ–Љ–∞—В–∞ –≤–і—П—Б–љ–Њ –µ –Є–Ј–Њ–±—А–∞–Ј–µ–љ–Њ —А–∞—Б—В–µ–љ–Є–µ—В–Њ Protea cynaroides –Є –Љ–Њ–ґ–µ –і–∞ —Б–µ –Ј–∞–±–µ–ї–µ–ґ–Є, —З–µ –≤—Б–µ–Ї–Є –Њ—Б–Љ–Є –ї–Є—Б—В –Ј–∞–µ–Љ–∞ —Б—К—Й–∞—В–∞ –≤–µ—А—В–Є–Ї–∞–ї–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П –Ї–∞—В–Њ –њ—К—А–≤–Є—П –ї–Є—Б—В –љ–∞ —Б—В—К–±–ї–Њ—В–Њ (0). –Ю—Б–≤–µ–љ —В–Њ–≤–∞, –≤—Б–µ–Ї–Є –Њ—Б–Љ–Є –ї–Є—Б—В –Є–і–≤–∞ —В–Њ—З–љ–Њ —Б–ї–µ–і —В—А–Є –Њ–±–Њ—А–Њ—В–∞ –Є–ї–Є 3 —Ж–Є–Ї—К–ї–∞ (–Њ–±–Њ—А–Њ—В–Є) –Ј–∞ –њ–µ—А–Є–Њ–і. –Р–Ї–Њ –±—А–Њ—П –љ–∞ –ї–Є—Б—В–∞—В–∞ –Ј–∞ –њ–µ—А–Є–Њ–і –µ n, –∞ –±—А–Њ—П –љ–∞ –Њ–±–Њ—А–Њ—В–Є—В–µ –Ј–∞ –њ–µ—А–Є–Њ–і вАУ m, —В–Њ P. cynaroides –Є–Љ–∞ m = 3 –Є n = 8: –і–≤–µ —З–Є—Б–ї–∞ –Њ—В –њ–Њ–Ј–љ–∞—В–∞—В–∞ –љ–Є —А–µ–і–Є—Ж–∞!
- m = 1, n = 2 - –ї–Є–њ–∞, –ґ–Є—В–љ–Є—В–µ –Ї—Г–ї—В—Г—А–Є–Є –Є –Љ–љ–Њ–≥–Њ –Њ—В –ї—Г–Ї–Њ–≤–Є—З–љ–Є—В–µ —А–∞—Б—В–µ–љ–Є—П;
- m = 1, n = 3 вАУ –µ–ї–∞, –±—Г–Ї, –ї–µ—Б–Ї–∞ –Є –±—А–µ–Ј–∞, –∞ —Б—К—Й–Њ –Є –ї–Њ–Ј–Є—В–µ;
- m =2, n = 5 - –Є–≤–∞, –і—К–±, —А–Њ–Ј–Є—В–µ –Є –љ—П–Ї–Њ–Є –њ–ї–Њ–і–љ–Є –Ї–Њ—Б—В–Є–ї–Ї–Њ–≤–Є –і—К—А–≤–µ—В–∞ –Ї–∞—В–Њ —П–±—К–ї–Ї–Є—В–µ –Є –≤–Є—И–љ–Є—В–µ –љ–∞–њ—А–Є–Љ–µ—А;
- m = 3 , n = 8 вАУ –Ј–µ–ї–µ, –∞—Б—В—А–Є, –Љ–∞–ї–Є–љ–Є, –Ї—А—Г—И–Є –Є —В–Њ–њ–Њ–ї–Є;
- m = 5 , n = 13 вАУ –±–∞–і–µ–Љ–Є;
- m = 8, n = 21 вАУ –Ј–∞ —Е–≤–Њ–є–љ–Њ–≤–Є—В–µ –Є –µ–ї–Њ–≤–Є—В–µ —И–Є—И–∞—А–Ї–Є;
- m = 13, n = 34 вАУ –±–Њ—А.
–Э–Њ –њ—А–Њ–±–ї–µ–Љ—К—В –µ, —З–µ —А–∞—Б—В–µ–љ–Є—П—В–∞ –љ–µ –≤–Є–љ–∞–≥–Є –њ–Њ–Ї–∞–Ј–≤–∞—В —З–Є—Б–ї–∞—В–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є, –∞ –і–∞–љ–љ–Є—В–µ –Ј–∞ —А–µ–∞–ї–љ–Њ—В–Њ —А–∞–Ј–љ–Њ–Њ–±—А–∞–Ј–Є–µ –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—В–µ –Љ–Њ–і–µ–ї–Є –њ—А–Є —А–∞—Б—В–µ–љ–Є—П—В–∞ –Є —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є—В–µ –љ–µ —Б–∞ –і–Њ—Б—В–∞—В—К—З–љ–Њ.
–Ч–∞—В–Њ–≤–∞ –Ь—Г–Ј–µ—П—В –љ–∞ –љ–∞—Г–Ї–∞—В–∞ –Є –Є–љ–і—Г—Б—В—А–Є—П—В–∞ –≤ –Ь–∞–љ—З–µ—Б—В—К—А –Є —Д–µ—Б—В–Є–≤–∞–ї—К—В –љ–∞ –љ–∞—Г–Ї–∞—В–∞ –≤ –Ь–∞–љ—З–µ—Б—В—К—А –≤ —З–µ—Б—В –љ–∞ —А–∞–±–Њ—В–∞—В–∞ –љ–∞ –≥–µ–љ–Є–∞–ї–љ–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Р–ї—К–љ –Ґ—О—А–Є–љ–≥, –Ї–Њ–Љ–њ—О—В—К—А–µ–љ —Г—З–µ–љ –Є —А–Њ–і–Њ–љ–∞—З–∞–ї–љ–Є–Ї –љ–∞ –Є–Ј–Ї—Г—Б—В–≤–µ–љ –Є–љ—В–µ–ї–µ–Ї—В –Ј–∞–њ–Њ—З–≤–∞—В –њ—А–Њ–µ–Ї—В, –Ї–Њ–є—В–Њ –і–∞ –њ—А–Њ–і—К–ї–ґ–Є —А–∞–±–Њ—В–∞—В–∞, –Ї–Њ—П—В–Њ –Ґ—О—А–Є–љ–≥ –Ј–∞–њ–Њ—З–≤–∞ –њ—А–µ–і–Є —Б–Љ—К—А—В—В–∞ —Б–Є –њ—А–µ–Ј 1954 –≥.
–Т –њ–Њ—Б–ї–µ–і–љ–Є—В–µ 4 –≥–Њ–і–Є–љ–Є —Г—З–µ–љ–Є, –ї—О–±–Є—В–µ–ї–Є-–µ—Б—В–µ—Б—В–≤–Њ–Є–Ј–њ–Є—В–∞—В–µ–ї–Є –Є –≥—А–∞–і–Є–љ–∞—А–Є –Є–Ј–њ—А–∞—Й–∞—В —Б–≤–Њ–Є —Б–љ–Є–Љ–Ї–Є –Є –і–Њ–Ї–ї–∞–і–Є –Ј–∞ –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞ —Б–њ–Є—А–∞–ї–Є –љ–∞ —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є. –Ю–±—Й–Њ —Г—З–µ–љ–Є—В–µ –∞–љ–∞–ї–Є–Ј–Є—А–∞—В 657 —Ж–≤—П—В–∞. –Т –њ—А–Њ—Г—З–≤–∞–љ–µ—В–Њ, –њ—Г–±–ї–Є–Ї—Г–≤–∞–љ–Њ –Њ—В Royal Society —Б–µ —Б—К–Њ–±—Й–∞–≤–∞, —З–µ –≤ —З–µ—В–Є—А–Є —Б–ї—Г—З–∞—П –Њ—В –≤—Б–µ–Ї–Є –њ–µ—В —Б–µ —Б—К–і—К—А–ґ–∞—В —З–Є—Б–ї–∞—В–∞ –Њ—В –њ–Њ—А–µ–і–Є—Ж–∞—В–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є, –∞ –Њ—Б—В–∞–љ–∞–ї–∞—В–∞ —З–∞—Б—В - –љ–∞ –њ–Њ–і–Њ–±–љ–Є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В–Є (–љ–∞–њ—А–Є–Љ–µ—А, —А–µ–і–∞ –љ–∞ –Ы—Г–Ї–∞ 1, 3, 4, 7, 11, 18, 29 –Є —В. –љ.), –Є–ї–Є –њ–Њ-—Б–ї–Њ–ґ–љ–Є –Љ–Њ–і–µ–ї–Є.
 –†–∞–Ј–њ—А–µ–і–µ–ї–µ–љ–Є–µ –љ–∞ —А–∞–Ј–ї–Є—З–љ–Є—В–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Љ–Њ–і–µ–ї–Є –љ–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В–Є –Њ—В –Є–Ј—Б–ї–µ–і–≤–∞–љ–µ—В–Њ.
–†–∞–Ј–њ—А–µ–і–µ–ї–µ–љ–Є–µ –љ–∞ —А–∞–Ј–ї–Є—З–љ–Є—В–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Љ–Њ–і–µ–ї–Є –љ–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В–Є –Њ—В –Є–Ј—Б–ї–µ–і–≤–∞–љ–µ—В–Њ.
–Т –Є–Ј—Б–ї–µ–і–≤–∞–љ–µ—В–Њ –Є–Љ–∞ –њ—А–Є–Љ–µ—А–Є –љ–∞ —Б–ї—К–љ—З–Њ–≥–ї–µ–і–Є, –њ–Њ–Ї–∞–Ј–≤–∞—Й–Є –Љ–Њ–і–µ–ї–Є –љ–∞ —Б–њ–Є—А–∞–ї–∞, –љ–Њ –љ–µ –≤–Є–љ–∞–≥–Є –њ–Њ —А–µ–і–∞ –љ–∞ –§–Є–±–Њ–љ–∞—З–Є, –Љ–∞–Ї–∞—А —З–µ —В–Њ–є –Є –љ–µ–≥–Њ–≤–Є –Љ–Њ–і–Є—Д–Є–Ї–∞—Ж–Є–Є –і–∞ –њ—А–µ–Њ–±–ї–∞–і–∞–≤–∞—В. –Ш–Ј—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–Є—В–µ —Б–Љ—П—В–∞—В, —З–µ —В–µ–Ј–Є –Є–Ј–Ї–ї—О—З–µ–љ–Є—П –Њ—В –њ—А–∞–≤–Є–ї–Њ—В–Њ —Б–∞ –Њ—В –Є–љ—В–µ—А–µ—Б –Ј–∞ –±—К–і–µ—Й–Њ –њ—А–Њ—Г—З–≤–∞–љ–µ –Є –Љ–Њ–ґ–µ –і–∞ —Б—В–∞–љ–∞—В –±–∞–Ј–∞ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ –љ–Њ–≤–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Љ–Њ–і–µ–ї–Є.


















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
–Э—П–Љ–∞ –Ї–Њ–Љ–µ–љ—В–∞—А–Є –Ї—К–Љ —В–∞–Ј–Є –љ–Њ–≤–Є–љ–∞ !
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
dolivo
–Ч–µ–Љ–љ–∞—В–∞ —П–±—К–ї–Ї–∞: —Б—В–∞—А–∞ –Ї—Г–ї—В—Г—А–∞ –Ј–∞ –љ–Њ–≤–Є—В–µ –Ї–ї–Є–Љ–∞—В–Є—З–љ–Є –≤—А–µ–Љ–µ–љ–∞
dolivo
–Ч–µ–Љ—П—В–∞ –њ–Њ—В—К–Љ–љ—П–≤–∞. –Ъ–∞–Ї–≤–Њ –Њ–Ј–љ–∞—З–∞–≤–∞ —В–∞–Ј–Є —В—А–µ–≤–Њ–ґ–љ–∞ –Ї–ї–Є–Љ–∞—В–Є—З–љ–∞ —В–µ–љ–і–µ–љ—Ж–Є—П –Ј–∞ –±—К–і–µ—Й–µ—В–Њ?
Nikor
–Э–∞ 30 —Б–µ–њ—В–µ–Љ–≤—А–Є 1928 –µ –Њ—В–Ї—А–Є—В –њ–µ–љ–Є—Ж–Є–ї–Є–љ—К—В
–Я—А–Њ—Б—В –І–Њ–≤–µ–Ї
–Э–Њ–≤–Њ –Њ–±—П—Б–љ–µ–љ–Є–µ –Ј–∞ –≥–Є–≥–∞–љ—В—Б–Ї–Є—В–µ –µ–Ї—Б–њ–ї–Њ–і–Є—А–∞—Й–Є –Ї—А–∞—В–µ—А–Є –≤ –°–Є–±–Є—А