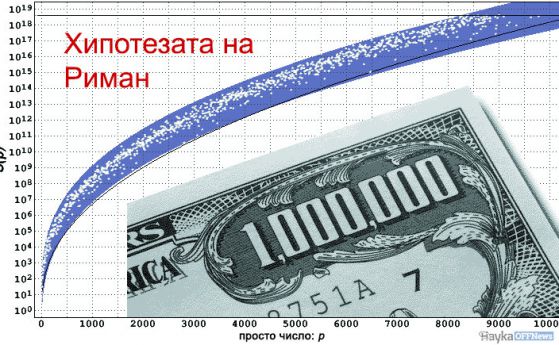
Миналата седмица нигерийският математик проф. Опиеми Енох (Opeyemi Enoch) обяви, че е намерил решение на една задача, за която Институтът Клей дава 1 млн долара - доказателството на хипотезата на Риман.
Хипотезата на Риман не е лесно да се формулира по начин, разбираем за нематематици, защото е същността на една трудна за разбиране математическа теория. Ето как звучи хипотезата на Риман:
Всички нетривиални нули на дзета-функцията имат реална част равна на ½
За обикновения читател, дори и добре образован, но без добра математическа подготовка, това е може би пълна безсмислица.
Ще се опитам да ви дам някаква представа за хипотезата на Риман като в никакъв случай не ви подтиквам да опитвате, въпреки примамливата награда, а по-скоро "не правете това у дома", ако не сте готов да загубите години и да намразите себе си.
През 1859 г., Бернхард Риман (Bernhard Riemann) публикува статия, в която излага един напълно нов метод за оценка за разпределението на простите числа.
Простите числа
Простите числа са особени с това, че не могат да се представят като произведение на две по-малки числа. Такива са например 2, 3, 5, 7, 11 и т.н. Те играят важна роля в чистата математика, а и в други области, изискващи целочислени решения.
Разпределението на простите числа между всички естествени числа изглежда не следва някаква закономерност.
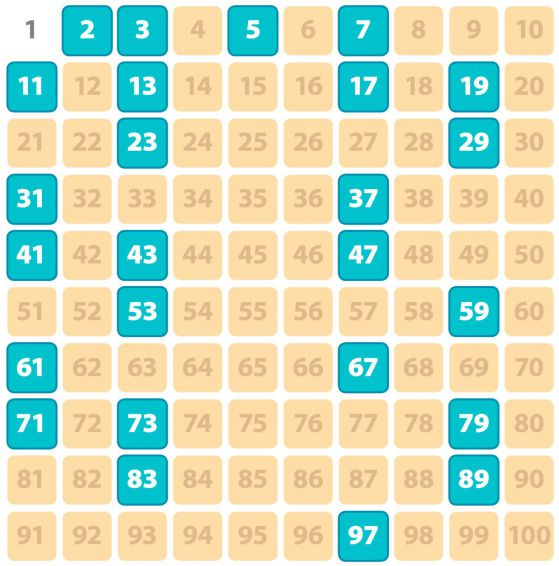
Немският математик Бернхард Риман забелязва през 1859, че честотата на простите числа е много тясно свързана с поведението на една сложна функция, която е открива Леонард Ойлер, но Риман взема тази идея и я развива по съвсем нов начин, чрез определяне на т.нар. дзета-функция.
Редът на Ойлер
Теоремата за разпределението на простите числа е отговор на евклидовата теоремата, че простите числа отиват в безкрайността и могат да бъдат произволно големи. Друга фундаментална евклидова теорема определя уникалността на разлагането на множители: всяко положително цяло число е произведение на прости числа, при това само с един уникален набор от множители. През 1737 Ойлер разбира, че първата теорема може да бъде преформулирана, а второто твърдение да се превърне в просто следствие на тази формула. Ето как:
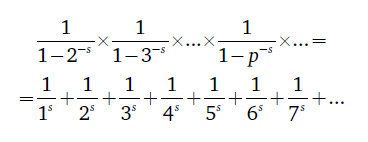
Тук р са всички прости числа (р = 2, 3, 5, 7), а s е константа. От лявата страна се умножават безкрайно много членове, които зависят само от прости числа. В дясната събираме безкраен брой членове, които зависят от всички положителни числа. Тази формула изразява връзката между цели и прости числа и уникалността на разлагането на множители. Но за да стане ясно за всички, трябва малко математика.
Редове - сходящи и несходящи
Ред, според математиците е неограничено продължаващо сумиране на членове, всеки от които се задава с някакъв общ закон. Да вземем например реда на естествените числа:
1 + 2 + 3 + 4 + 5 + 6 + 7 + ...
Ако съберем произволен брой членове на този ред, ще получим произволно голям резултат.
Да вземем например членовете на реда 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, … - това са обратните (реципрочните) стойности на обикновените естествени числа 1, 2, 3, 4, 5, 6, 7, ….
Редът 1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + ….. играе важна роля математиката и си има свое име - хармоничен ред.
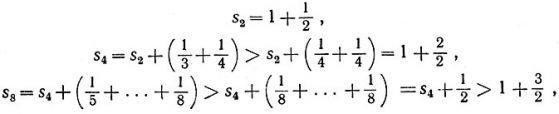
И макар че членовете на хармоничния ред намаляват, все пак сумата расте и също може да получим произволно голям резултат, което се вижда от горните сметки.
Тази сума няма ограничение. Хармоничният ред е разходящ или несходящ, както и редът на естествените числа.
Но ако повдигнем на квадрат знаменателите на хармоничния ред, полученият ред е сходящ:
Нека да разгледаме последователността на частичните суми:
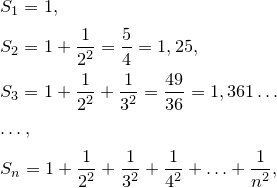
Резултатите, които се получават, ще бъдат все по-близки до числото π2/6=1.644934..., но никога няма да го надскочат. Казано по математически: редът клони към π2/6, или сумата на реда е равна на π2/6.
Сега нека да видим какво ще стане, ако вместо да повдигаме естествените числа в знаменателя на квадрат, да ги повдигнем на каква да е друга степен? Оказва се, че съответната сума
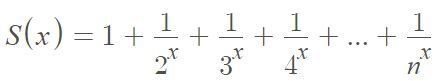
е сходяща, ако степента x е число, по-голямо от 1. има определена крайна стойност.
S(x) е точно това, което се нарича дзета-функция, формулирана от Леонард Ойлер, велик математик на XVII век. Точно за нея се споменава в хипотезата на Риман.
Дзета-функцията
До тук добре - за всяко x > 1 редът на Ойлер е сходящ.
Но какво ще стане, ако разгледаме числата, по-малки от 1 ? Например, ако x = - 1 ?
Така стигаме до реда на естествените числа, който знаем е несходящ. Същото важи и за други стойности по-малки от x или равни на 1. Сумата е разходяща.
Продължение на дзета-функцията на Ойлер
Излезе, че разглежданата дзета-функция на Ойлер S(x) е определена за реални числа x по-големи от 1. Реалните числа са част от по-голяма група числа, наречени комплексни числа. И докато реалните числа съответстват на всички точки на числовата ос, комплексните числа съответстват на всички точки на равнината, съдържаща реалната числова права. Тази равнина се нарича комплексна равнина. И точно както функцията се определя от аргументи, които са реални числа, точно така може да дефинираме функцията като аргументи са й комплексни числа.
Един интересен факт, свързан с функциите на комплексните променливи е, че ако знаете стойностите на функцията за някакво множество данни, то може да се научат стойностите на функцията във всяка точка в комплексната равнина.
Този метод за разширяване на областта на функцията е известен като аналитично продължение. Дзета-функцията на Ойлер е определена за реални числа по-големи от 1. Тъй като реалните числа са комплексни числа, можем да считаме тази функция като комплексна функция, а след това да използваме аналитичното продължаване, за да получим нова функция, дефинирана за цялата равнина, но съгласувана с дзета-функцията на Ойлер за реални числа по-големи от 1.
Риман разбира, че дзета-функцията е ключът към теоремата за разпределението на простите числа, но за да се приложи този подход, трябва да се разшири, да се определи дзета-функцията не само за реални, но и за комплексни променливи.
Има още едно нещо, което може да се направи. С помощта на комплексния математичен анализ, може да се разшири областта на определение на дзета-функцията на Ойлер така, че за числа по-малки или равни на 1 функцията да приема крайни стойности. С други думи, има начин да се определи нова функция, която ще наречем ζ (x) :
ζ(x) = S(x) = 1/1x + 1/2x + 1/3x + 1/4x + … .
За x > 1 и за x < 1 функцията ζ(x) ще приема определени крайни стойности. Този метод се нарича аналитично продължение и новата функция, която се получава, се нарича дзета-функцията на Риман. Създаването на тази нова функция приемаща крайни стойности и за x < 1 се състои в изваждането от несходящия ред на друг несходящ ред. Така от безкрайността, получаваща се от първата разходяща сума минус безкрайността, която дава втората разходяща сума, се получава нещо крайно.
Риман разбира, че дзета-функцията е ключът към теоремата за разпределението на простите числа, но за да се приложи този подход, трябва да се разшири: да се определи дзета-функцията не само за реални, но и за комплексни променливи.
Риман разширява определението на ζ (x) за всички комплексни числа освен 1. Единицата е изключена, защото за x = 1, стойността на дзета-функцията става безкрайна.
През 1859 г. Риман представя идеите си за дзета-функцията в статия със заглавие "За количеството на простите числа, ненадвишаващи определена стойност". В нея представя пълната и точна функция на разпределение на простите числа.
Тривиални и нетривиални нули
Риман успял да покаже, че разпределението на простите числа зависи от това къде дзета-функцията се нулира. Тя има така наречените тривиални нули в четните отрицателни числа (–2, –4, –6, …). Те са тривиални в смисъл, че тяхното съществуване може да се докаже сравнително лесно (например използвайки функционалното уравнение).
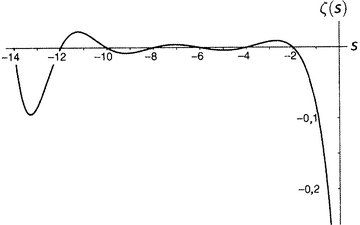
Всички останали нули се наричат нетривиални. Задачата се състои в това, да се опишат всички останали нули на дзета-функцията. А всички нетривиални нули на дзета-функцията се получават за комплексни числа. Те лежат на критичната линия, а реалната им част, равна на 1/2. Това е и забележителната хипотеза на Риман.
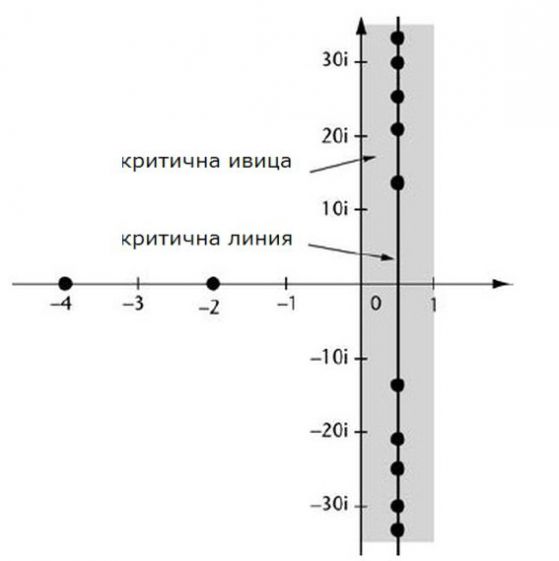
Нулите на дзета-функцията, критичната линия и критичната ивица
150 години нерешима
Доказателството на хипотезата на Риман е проблемът, който вече 150 години измъчва най-талантливите математици на Земята. Местоположението на нулите на дзета-функцията е от огромна важност за теорията на числата. Информацията за нетривиалните нули дава отговори и на други въпроси извън математиката.
Никой досега не я е доказал, но малцина са тези, които се съмняват, че хипотезата на Риман е вярна. Числените експерименти са повече от убедителни - вече са изчислени първите 1013 нули на Римановата дзета-функция и строго е установено, че повече от 40% от нулите на дзета-функции удовлетворяват хипотезата.
Ефектът на Казимир
През 1948 г. холандският учен Хендрик Казимир (Hendrik Casimir) прогнозира ефект, който днес носи неговото име. Той дълго време е само елегантна теоретична идея, но вече е експериментално потвърден и в него играе роля дзета-функцията.
Какво представлява този ефект:
Ако се вземат две незаредени близко разположени металните пластини с отразяващи повърхности на разстояние от няколко атомни диаметри, те ще бъдат привлечени една към друга заради флуктуациите на разположения между тях вакуум, който непрекъснато произвежда двойки частици и античастици. В пространството помежду пластините се получават резонансни вълни, които цяло или полуцяло число пъти се поместват между повърхностите като електромагнитните вълни се усилват.
 |
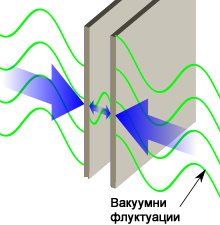| Илюстрация: wikipedia |
Всички останали дължини, които са по-големи, се потискат, т.е. се потиска раждането на съответните виртуални фотони. Това се дължи на факта, че в пространството между пластините може да съществуват само стоящи вълни, чиято амплитуда е равна на нула. В резултат на това налягането на виртуалните фотони между двете повърхности е по-малко от налягането върху тях отвън, там, където раждането на фотони е неограничено. Колкото по-близо една до друга са повърхностите, толкова по-малка е дължината на вълните в резонанс и толкова повече се оказват потушени. В резултат на това, се увеличава силата на привличане между повърхностите.
Този ефект донякъде е подобен на привличането на плуващи прекалено близо един до друг кораби в океана.,
Силата, с която се привличат пластините е пропорционална на сумата на честотите на стоящите вълни, генерирани между плочите.
Ако се направи опит да се изчисли общата плътност на енергията между двете плочи, с помощта на математиката или квантовата физика, ще се получи една безкрайна сума:
1 + 8 + 27 + 64 + ...
Тази безкрайна сума е същото, което ще получите, когато зададете стойността x = - 3 в дзета- функцията на Ойлер:
За съжаление тази сума е разходяща (и то още по-бързо, отколкото S(-1) ), което би означавало безкрайна плътност на енергията . Това очевидно е пълна глупост. Но какво, ако предположим, че безкрайната сума е равно на дзета-функция на Риман, а не дзета-функция на Ойлер за x = - 3? Тогава може да се получи крайна плътност на енергията. Това означава, че трябва да има сила на привличане между металните плочи, които също изглежда невероятно, тъй като според класическата физика, не трябва да има никакви сили.
Но ето, че изненадващо когато физиците поставят експеримента, откриват, че силата наистина съществува и съответства на плътността на енергията точно равна на ζ( - 3).
Като че ли природата следва идеята на Риман - тя разширява дзета-функцията на Ойлер, да се включат стойности на x, които са по-малки от 1, изваждайки безкрайността, за да се получи крайна стойност. Удивително!
Източници:
Infinity or -1/12? , David Berman and Marianne Freiberger
Riemann Hypothesis, Clay Mathematics Institute (CMI)
"Prime Obsession", John Derbyshire
Что такое математика?, 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin х в виде бесконечного произведения, Рихард Курант, Герберт Роббинс
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
23.11 2015 в 12:48
22.11 2015 в 18:24
Продължавайте все така! :)
Последни коментари