

–У—А—Г–њ–∞ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П –µ —Б—К–≤–Ї—Г–њ–љ–Њ—Б—В—В–∞ –Њ—В –≤—Б–Є—З–Ї–Є –Њ—А—В–Њ–≥–Њ–љ–∞–ї–љ–Є –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є—П, –њ—А–Є –Ї–Њ–Є—В–Њ –љ—П–Ї–∞–Ї–≤–∞ —Д–Є–≥—Г—А–∞ ( —В—П–ї–Њ) —Б—К–≤–њ–∞–і–∞ —Б–∞–Љ–∞ —Б—К—Б —Б–µ–±–µ —Б–Є. –Ґ–µ–Ј–Є —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є–Є —Б–µ –љ–∞—А–Є—З–∞—В —Б–Є–Љ–µ—В—А–Є—П. –Х–ї–µ–Љ–µ–љ—В–Є –љ–∞ —Б–Є–Љ–µ—В—А–Є—П—В–∞ —Б–∞:¬†—Ж–µ–љ—В—К—А –љ–∞ —Б–Є–Љ–µ—В—А–Є—П;¬†—А–∞–≤–љ–Є–љ–∞ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П;¬†–Њ—Б –љ–∞ —Б–Є–Љ–µ—В—А–Є—П.
–Т–Є–і–Њ–≤–µ —Б–Є–Љ–µ—В—А–Є—П
–°–Є–Љ–µ—В—А–Є—П—В–∞ —Б–њ—А—П–Љ–Њ —А–∞–≤–љ–Є–љ–∞ (–Њ–≥–ї–µ–і–∞–ї–љ–∞, –і–≤—Г—Б—В—А–∞–љ–љ–∞, –±–Є–ї–∞—В–µ—А–∞–ї–љ–∞¬† —Б–Є–Љ–µ—В—А–Є—П)
 |
 |
 |
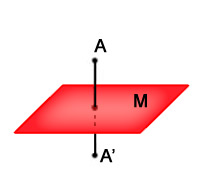
–Ф–≤–µ —В–Њ—З–Ї–Є –Р –Є –Р' —Б–∞ —Б–Є–Љ–µ—В—А–Є—З–љ–Є –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–∞ —А–∞–≤–љ–Є–љ–∞—В–∞ M, –∞–Ї–Њ —Б–∞ —А–∞–Ј–њ–Њ–ї–Њ–ґ–µ–љ–Є –љ–∞ –µ–і–љ–∞ –њ—А–∞–≤–∞, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –љ–∞ M, –љ–∞ –µ–і–љ–Њ –Є —Б—К—Й–Њ —А–∞–Ј—Б—В–Њ—П–љ–Є–µ –Њ—В –љ–µ—П. –§–Є–≥—Г—А–Є –Є —В–µ–ї–∞ —Б–∞ —Б–Є–Љ–µ—В—А–Є—З–љ–Є —Б–њ—А—П–Љ–Њ —А–∞–≤–љ–Є–љ–∞—В–∞ M, –∞–Ї–Њ –Ј–∞ –≤—Б—П–Ї–∞ —В–Њ—З–Ї–∞ –Њ—В —В—П–ї–Њ—В–Њ, —Б—К—Й–µ—Б—В–≤—Г–≤–∞ —Б–Є–Љ–µ—В—А–Є—З–љ–∞ —Б–њ—А—П–Љ–Њ —А–∞–≤–љ–Є–љ–∞—В–∞ –і—А—Г–≥–∞ —В–Њ—З–Ї–∞ –Њ—В —В—П–ї–Њ—В–Њ. –Р–Ї–Њ —Б–µ –≤—К–≤–µ–і–µ –≤ –і–µ–Ї–∞—А—В–Њ–≤–∞ –Њ—Б –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞ Z, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –љ–∞ —А–∞–≤–љ–Є–љ–∞—В–∞ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П M (XY), –≤—Б—П–Ї–∞ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ —Й–µ —Б–µ –њ–Њ–і–і—К—А–ґ–∞ –њ—А–Є –њ—А–Њ–Љ—П–љ–∞ –љ–∞ –Ј–љ–∞–Ї–∞ –љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є—В–µ F(x,y,z) = F(x,y,-z). –С–µ–ї–µ–ґ–Є —Б–µ –љ–∞–є-—З–µ—Б—В–Њ —Б –Ь.
–Ю—Б–µ–≤–∞ —Б–Є–Љ–µ—В—А–Є—П (—А–Њ—В–∞—Ж–Є–Њ–љ–љ–Њ-—Ж–Є–ї–Є–љ–і—А–Є—З–љ–∞)
 –°–љ–Є–Љ–Ї–∞: Marine Ecology at Central Missouri State University in Jamaica –°–љ–Є–Љ–Ї–∞: Marine Ecology at Central Missouri State University in Jamaica |
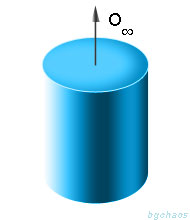 |
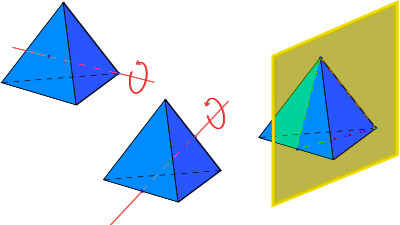
–Ґ—П–ї–Њ—В–Њ –Є–Љ–∞ –Њ—Б –љ–∞ —Б–Є–Љ–µ—В—А–Є—П n-—В–Є —А–µ–і –Юn, –∞–Ї–Њ –њ—А–Є –≤—К—А—В–µ–љ–µ –Њ–Ї–Њ–ї–Њ —В–∞–Ј–Є –Њ—Б, —В—П–ї–Њ—В–Њ n –њ—К—В–Є¬† —Б—К–≤–њ–∞–і–∞ —Б—К—Б —Б–µ–±–µ —Б–Є, –∞ –Ј–∞–≤—К—А—В–∞–љ–Є—П—В–∞ —Б–∞ 360¬∞/n. –°–∞–Љ–∞—В–∞ –Њ–њ–µ—А–∞—Ж–Є—П –љ–∞ —Б–Є–Љ–µ—В—А–Є—П —Б–µ –±–µ–ї–µ–ґ–Є —Б—К—Б Cn , –Ї—К–і–µ—В–Њ n e –њ–Њ—А—П–і—К–Ї—К—В –љ–∞ —Б–Є–Љ–µ—В—А–Є—П. –Р–Ї–Њ –µ–і–љ–Њ —В—П–ї–Њ —Б—К–≤–њ–∞–і–∞ —Б–∞–Љ–Њ —Б—К—Б —Б–µ–±–µ —Б–Є, –Ї–Њ–≥–∞—В–Њ —Б–µ –Ј–∞–≤—К—А—В–∞ –љ–∞ –Ї–∞–Ї—К–≤—В–Њ –Є –і–∞ –µ —К–≥—К–ї, —В–∞–Ї–Њ–≤–∞ —В—П–ї–Њ —Б–µ –љ–∞—А–Є—З–∞ –Њ—Б–µ–≤–Њ—Б–Є–Љ–µ—В—А–Є—З–љ–Њ, –∞ –њ—А–∞–≤–∞—В–∞, –Њ–Ї–Њ–ї–Њ –Ї–Њ—П—В–Њ —Б–µ –Є–Ј–≤—К—А—И–≤–∞ –Ј–∞–≤—К—А—В–∞–љ–µ—В–Њ –љ–∞ –њ—А–Њ–Є–Ј–≤–Њ–ї–µ–љ —К–≥—К–ї —Б–µ –љ–∞—А–Є—З–∞ –Њ—Б –љ–∞ —Б–Є–Љ–µ—В—А–Є—П.
–Т —В–Њ–Ј–Є —Б–ї—Г—З–∞–є –Њ—Б—В–∞ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П –Љ–Њ–ґ–µ –і–∞ —Б–µ —А–∞–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –Њ—Б –љ–∞ —Б–Є–Љ–µ—В—А–Є—П –Њ—В –±–µ–Ј–Ї—А–∞–µ–љ —А–µ–і OвИЮ –Є —Б–µ –њ—А–µ–≤—А—К—Й–∞ –≤ –њ—А–µ–і–µ–ї–љ–∞ –≥—А—Г–њ–∞. –Э–∞–є-–њ—А–Њ—Б—В–∞—В–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–∞ —Д–Є–≥—Г—А–∞, –Ї–Њ—П—В–Њ –Є–Љ–∞ –Њ—Б –љ–∞ —Б–Є–Љ–µ—В—А–Є—П –Њ—В –±–µ–Ј–Ї—А–∞–µ–љ —А–µ–і OвИЮ, –µ —Ж–Є–ї–Є–љ–і—К—А—К—В, –Ј–∞—В–Њ–≤–∞ —В–Њ–Ј–Є —В–Є–њ —Б–Є–Љ–µ—В—А–Є—П —Б–µ –љ–∞—А–Є—З–∞ –Њ—Й–µ —Ж–Є–ї–Є–љ–і—А–Є—З–љ–∞ —Б–Є–Љ–µ—В—А–Є—П.
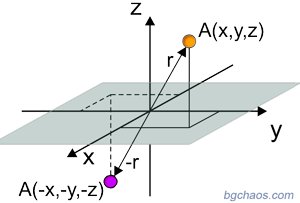
–°–Є–Љ–µ—В—А–Є—П –Є–љ–≤–µ—А—Б–Є—П–Х–і–Є–љ –љ–µ —В–Њ–ї–Ї–Њ–≤–∞ –њ–Њ–Ј–љ–∞—В –≤–Є–і —Б–Є–Љ–µ—В—А–Є—П. –Т—Б—П–Ї–∞ —В–Њ—З–Ї–∞ —Б–µ –њ—А–Њ–µ–Ї—В–Є—А–∞ –њ—А–µ–Ј –љ–∞—З–∞–ї–Њ—В–Њ –љ–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В–љ–∞—В–∞ —Б–Є—Б—В–µ–Љ–∞, —Б–њ—А—П–Љ–Њ —Ж–µ–љ—В—К—А–∞ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П—В–∞, –Є–љ–≤–µ—А—Б–Є—П –≤ –і–Є–∞–Љ–µ—В—А–∞–ї–љ–Њ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П. –Т—Б–Є—З–Ї–Є –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є –њ—А–Њ–Љ–µ–љ—П—В –Ј–љ–∞–Ї–∞ —Б–Є: F(x,y,z) =¬†F(-x,-y,-z). –Ю–±–Њ–Ј–љ–∞—З–∞–≤–∞ —Б–µ —Б I. |
 |
–†–Њ—В–Њ—А–µ—Д–ї–µ–Ї—В–Њ—А–љ–∞ —Б–Є–Љ–µ—В—А–Є—П–†–Њ—В–Њ—А–µ—Д–ї–µ–Ї—В–Њ—А–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –µ –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П –Љ–µ–ґ–і—Г –Њ—Б–µ–≤–∞ –Є –Њ–≥–ї–µ–і–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П: —А–Њ—В–∞—Ж–Є—П –Њ–Ї–Њ–ї–Њ –Њ—Б, –≤ —Б—К—З–µ—В–∞–љ–Є–µ —Б –Њ—В—А–∞–ґ–µ–љ–Є–µ —Б–њ—А—П–Љ–Њ —А–∞–≤–љ–Є–љ–∞, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–∞ –љ–∞ —В–∞–Ј–Є –Њ—Б. –Э–∞ –Є–ї—О—Б—В—А–∞—Ж–Є—П—В–∞ –≤–і—П—Б–љ–Њ –≥–Є—А–Є—З–Ї–∞—В–∞ —Б—К—З–µ—В–∞–≤–∞ –Њ—Б–µ–≤–∞ —Б–Є–Љ–µ—В—А–Є—П –Њ—В 6-—В–Є –њ–Њ—А—П–і—К–Ї –Є –Њ–≥–ї–µ–і–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П. –°–њ–Њ—А–µ–і –≤—К–Ј–њ—А–Є–µ—В–Є—В–µ –Њ–Ј–љ–∞—З–µ–љ–Є—П —Б–µ –±–µ–ї–µ–ґ–Є –Ї–∞—В–Њ S6. –Ъ—Г–±—К—В –Є –Њ–Ї—В–∞–µ–і—К—А—К—В –Є–Љ–∞—В —А–Њ—В–Њ—А–µ—Д–ї–µ–Ї—В–Њ—А–љ–∞ —Б–Є–Љ–µ—В—А–Є—П S4. |
 |
–Ф–Є–µ–і—А–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П
–Ф–Є–µ–і—А–∞–ї–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –µ —Б—К—Й–Њ –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П –Љ–µ–ґ–і—Г –Њ—Б–µ–≤–∞ –Є –Њ–≥–ї–µ–і–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П: —А–Њ—В–∞—Ж–Є—П –Њ–Ї–Њ–ї–Њ –Њ—Б, –∞ –њ—А–µ–Ј –≤—Б–µ–Ї–Є –ї—К—З –Љ–Є–љ–∞–≤–∞ —А–∞–≤–љ–Є–љ–∞ –љ–∞ –Њ—В—А–∞–ґ–µ–љ–Є–µ. –Ґ–∞–Ї–∞–≤–∞ —Б–Є–Љ–µ—В—А–Є—П –Є–Љ–∞—В –њ—А–∞–≤–Є–ї–љ–Є—В–µ –Љ–љ–Њ–≥–Њ—К–≥—К–ї–љ–Є—Ж–Є –Є "–Ј–≤–µ–Ј–і–Є". –Ь–Њ—А—Б–Ї–Є—В–µ –Ј–≤–µ–Ј–і–Є –Є–Љ–∞—В –і–Є–µ–і—А–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П, –Ј–∞—Й–Њ—В–Њ –≤—Б–µ–Ї–Є –ї—К—З –Є–Љ –µ —Б–∞–Љ –њ–Њ —Б–µ–±–µ —Б–Є –і–≤—Г—Б—В—А–∞–љ–љ–Њ—Б–Є–Љ–µ—В—А–Є—З–µ–љ, —Б–љ–µ–ґ–Є–љ–Ї–Є—В–µ —Б–∞ —Б—К—Й–Њ —Б –і–Є–µ–і—А–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П.
 |
 |
 |
 |
–°–љ–Є–Љ–Ї–Є—В–µ —Б–∞ –Њ—В —Б–∞–є—В–∞: SnowCrystals.com
–°–љ–µ–ґ–Є–љ–Ї–Є—В–µ, –Њ–±—Й–Њ –≤–Ј–µ—В–Њ, –Є–Љ–∞—В —Б–Є–Љ–µ—В—А–Є—П –Њ—В 6-—В–Є –њ–Њ—А—П–і—К–Ї –Ї–∞—В–Њ –≤—Б—П–Ї–∞ –Њ—Б –Њ—В –Њ—Б–µ–≤–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –Є –Њ—Б –љ–∞ –Њ–≥–ї–µ–і–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П –Ј–∞ –≤—Б–µ–Ї–Є –ї—К—З.¬†–Я—А–Є–µ—В–Њ –µ –і–∞ —Б–µ –±–µ–ї–µ–ґ–Є —Б Dn¬†(–∞ –њ–Њ–љ—П–Ї–Њ–≥–∞ –Є Dih¬†n¬†) –Ј–∞ –њ—А–∞–≤–Є–ї–µ–љ –Љ–љ–Њ–≥–Њ—К–≥—К–ї–љ–Є–Ї —Б¬†n¬†—Б—В—А–∞–љ–Є –Э–Њ –њ–Њ –Ї–∞–Ї—К–≤ –љ–∞—З–Є–љ –≤—Б–µ–Ї–Є –Њ—В 6-—В–µ –ї—К—З–∞ –љ–∞ —Б–љ–µ–ґ–Є–љ–Ї–∞—В–∞ "–Ј–љ–∞–µ" –Ї–Њ–ї–Ї–Њ –Є —Б –Ї–∞–Ї–≤–Є —Д–Њ—А–Љ–Є —Б–∞ –њ–Њ—А–∞—Б—В–љ–∞–ї–Є –і—А—Г–≥–Є—В–µ –ї—К—З–Є? –§–Є–Ј–Є–Ї—К—В –Њ—В –Э–Р–°–Р –°–∞–Љ—Г–µ–ї –Ґ–Њ–ї–∞–љ—Б–Ї–Є (Samuel Tolansky) –Є–Ј–Ї–∞–Ј–≤–∞ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ—В–Њ, ¬†—З–µ –њ–∞–і–∞—Й–Є—В–µ —Б–љ–µ–ґ–Є–љ–Ї–Є, –Ї–Њ–Є—В–Њ –њ—А–µ–Љ–Є–љ–∞–≤–∞—В –њ—А–µ–Ј —Б—В—Г–і–µ–љ–Є—П –≤—К–Ј–і—Г—Е –Є —Г–ї–∞–≤—П—В –≤–Њ–і–љ–∞—В–∞ –њ–∞—А–∞, –≤–Є–±—А–Є—А–∞—В —Б–њ–Њ—А–µ–і —Б–Є–Љ–µ—В—А–Є—П—В–∞ –љ–∞ –Ї—А–Є—Б—В–∞–ї–љ–∞—В–∞ —Б–Є —Б—В—А—Г–Ї—В—Г—А–∞ –Є —В–µ–Ј–Є –≤–Є–±—А–∞—Ж–Є–Є –Њ–њ—А–µ–і–µ–ї—П—В –Ї–∞–Ї –Є —Б –Ї–∞–Ї–≤–Є —Д–Њ—А–Љ–Є —Й–µ —А–∞—Б—В–µ –Ї—А–Є—Б—В–∞–ї—К—В.
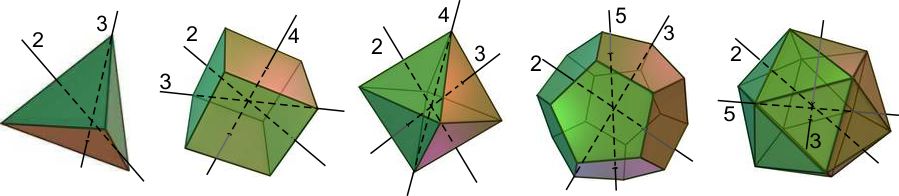
–†–Њ—В–∞—Ж–Є–Њ–љ–љ–∞ —Б–Є–Љ–µ—В—А–Є—П –љ–∞ –Я–ї–∞—В–Њ–љ–Њ–≤–Є—В–µ —В–µ–ї–∞
 –°—Е–µ–Љ–∞: websters-online-dictionary.org –°—Е–µ–Љ–∞: websters-online-dictionary.org |
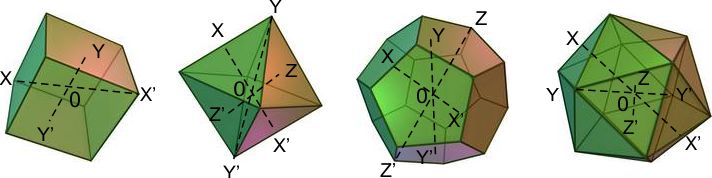
¬†–Ґ–µ—В—А–∞–µ–і—К—А—К—В –Є–Љ–∞ 4 –Њ—Б–Є –Њ—В —В—А–µ—В–Є –њ–Њ—А—П–і—К–Ї, –Љ–Є–љ–∞–≤–∞—Й–Є –њ—А–µ–Ј –≤—Б–µ–Ї–Є –≤—А—К—Е –Є —Б—А–µ–і–∞—В–∞ –љ–∞ —Б—А–µ—Й—Г–њ–Њ–ї–Њ–ґ–љ–∞—В–∞ —Б—В—А–∞–љ–∞, –∞ —Б—К—Й–Њ –Є 3 –Њ—Б–Є –Њ—В –≤—В–Њ—А–Є –њ–Њ—А—П–і—К–Ї –њ—А–µ–Ј —Б—А–µ–і–∞—В–∞ –љ–∞ –≤—Б—П–Ї–∞ –і–≤–Њ–є–Ї–∞ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —А—К–±–Њ–≤–µ |
–°—А–∞–≤–љ–Є—В–µ–ї–љ–∞ —В–∞–±–ї–Є—Ж–∞ –љ–∞ –Њ—Б–Є—В–µ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П –љ–∞ –Я–ї–∞—В–Њ–љ–Њ–≤–Є—В–µ —В–µ–ї–∞
| –Ю—Б–Є –њ–Њ—А—П–і—К–Ї: –Ґ–µ–ї–∞: | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| –Ґ–µ—В—А–∞–µ–і—К—А | –њ—А–µ–Ј —Б—А–µ–і–∞—В–∞ –љ–∞ –≤—Б—П–Ї–∞ –і–≤–Њ–є–Ї–∞ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —А—К–±–Њ–≤–µ | –Љ–Є–љ–∞–≤–∞—В –њ—А–µ–Ј –≤—Б–µ–Ї–Є –≤—А—К—Е –Є —Б—А–µ–і–∞—В–∞ –љ–∞ —Б—А–µ—Й—Г–њ–Њ–ї–Њ–ґ–љ–∞—В–∞ —Б—В—А–∞–љ–∞ | ||
| –Ъ—Г–± | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –≤—Б–µ–Ї–Є –љ–∞–±–Њ—А –Њ—В –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —А—К–±–Њ–≤–µ | –њ–Њ –≤—Б–µ–Ї–Є –≤—К—В—А–µ—И–µ–љ –і–Є–∞–≥–Њ–љ–∞–ї (–њ—А–µ–Ј –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є –≤—К—А—Е–Њ–≤–µ) | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –≤—Б—П–Ї–∞ –і–≤–Њ–є–Ї–∞ —Б—А–µ—Й—Г–њ–Њ–ї–Њ–ґ–љ–Є –Ї–≤–∞–і—А–∞—В–љ–Є —Б—В–µ–љ–Є | |
| –Ю–Ї—В–∞–µ–і—К—А | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –і–≤–Њ–є–Ї–∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —А—К–±–Њ–≤–µ | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –≤—Б—П–Ї–∞ –і–≤–Њ–є–Ї–∞ –Њ—В –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —В—А–Є—К–≥—К–ї–љ–Є —Б—В–µ–љ–Є | –Љ–Є–љ–∞–≤–∞—В –њ—А–µ–Ј –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є –≤—К—А—Е–Њ–≤–µ | |
| –Ф–Њ–і–µ–Ї–∞–µ–і—К—А | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –і–≤–Њ–є–Ї–∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —А—К–±–Њ–≤–µ | –Љ–Є–љ–∞–≤–∞—В –њ—А–µ–Ј –і–≤–Њ–є–Ї–∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є –≤—К—А—Е–Њ–≤–µ | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –≤—Б—П–Ї–∞ –і–≤–Њ–є–Ї–∞ –њ–µ—В–Њ—К–≥—К–ї–љ–Є —Б—В–µ–љ–Є | |
| –Ш–Ї–Њ—Б–∞–µ–і—К—А | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –і–≤–Њ–є–Ї–∞ –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —А—К–±–Њ–≤–µ | –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –љ–∞ –≤—Б—П–Ї–∞ –і–≤–Њ–є–Ї–∞ –Њ—В –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є —В—А–Є—К–≥—К–ї–љ–Є —Б—В–µ–љ–Є | –Љ–Є–љ–∞–≤–∞—В –њ—А–µ–Ј –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ–Є –≤—К—А—Е–Њ–≤–µ |
 –°—Е–µ–Љ–Є: bgchaos, –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ —Д–Є–≥—Г—А–Є –Њ—В Wikipedia ¬†
–°—Е–µ–Љ–Є: bgchaos, –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ —Д–Є–≥—Г—А–Є –Њ—В Wikipedia ¬†
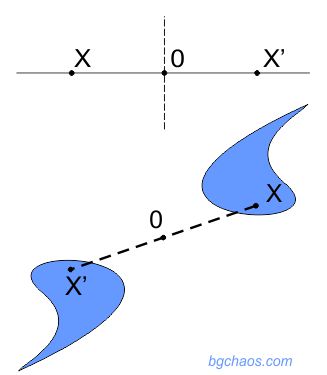
–°—Д–µ—А–Є—З–љ–∞ (—Ж–µ–љ—В—А–∞ћБ–ї–љ–∞) —Б–Є–Љ–µ—В—А–Є—П–¶–µ–љ—В—А–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–∞ —В–Њ—З–Ї–∞ –Ю –µ —В—А–∞–љ—Б—Д–Њ—А–Љ–∞—Ж–Є—П –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ, –њ—А–Є –Ї–Њ—П—В–Њ —В–Њ—З–Ї–∞ X —Б–µ –њ—А–Њ–µ–Ї—В–Є—А–∞ –Ї–∞—В–Њ —В–Њ—З–Ї–∞ –•', —В–∞–Ї–∞ —З–µ —В.–Ю –і–∞ –µ –≤ —Б—А–µ–і–∞—В–∞ –љ–∞ –Њ—В—Б–µ—З–Ї–∞—В–∞ XX'. –Ґ–Њ—З–Ї–∞ –Ю —Б–µ –љ–∞—А–Є—З–∞ —Ж–µ–љ—В—К—А –љ–∞ —Б–Є–Љ–µ—В—А–Є—П. –Т –µ–і–љ–Њ–Љ–µ—А–љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ (–њ—А–∞–≤–∞), —Ж–µ–љ—В—А–∞–ї–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –µ —А–∞–≤–љ–Њ—Б–Є–ї–љ–∞ –љ–∞ –Њ–≥–ї–µ–і–∞–ї–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П. –Т –і–≤—Г–Љ–µ—А–љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –µ —А–∞–≤–љ–Њ—Б–Є–ї–љ–∞ –љ–∞ –Ј–∞–≤—К—А—В–∞–љ–µ –љ–∞ 180¬∞ –Њ–Ї–Њ–ї–Њ —Ж–µ–љ—В—К—А–∞ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П. |
 |
–Т 4-–Љ–µ—А–љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ —Ж–µ–љ—В—А–∞–ї–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–і—Б—В–∞–≤–Є –Ї–∞—В–Њ –Ї–Њ–Љ–њ–Њ–Ј–Є—Ж–Є—П –Њ—В –і–≤–µ –Ј–∞–≤—К—А—В–∞–љ–Є—П –љ–∞ 180¬∞ –Њ–Ї–Њ–ї–Њ –і–≤–µ –≤–Ј–∞–Є–Љ–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є —А–∞–≤–љ–Є–љ–Є, –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є –≤ 4-–Љ–µ—А–µ–љ —Б–Љ–Є—Б—К–ї, –µ—Б—В–µ—Б—В–≤–µ–љ–Њ.
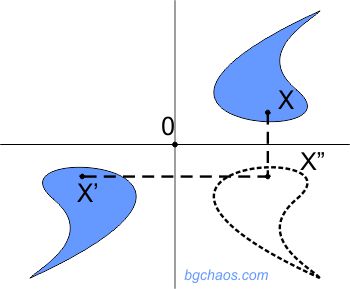 |
–¶–µ–љ—В—А–∞–ї–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–і—Б—В–∞–≤–Є –≤¬†n-–Љ–µ—А–љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Ї–∞—В–Њ –Ї–Њ–Љ–њ–Њ–Ј–Є—Ж–Є—П¬† –Њ—В n¬†–њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Є¬†–Њ—В—А–∞–ґ–µ–љ–Є—П¬†–Њ—В–љ–Њ—Б–љ–Њ¬†n¬†–≤–Ј–∞–Є–Љ–љ–Њ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ–Є¬†—Е–Є–њ–µ—А—А–∞–≤–љ–Є–љ–Є, –Љ–Є–љ–∞–≤–∞—Й–Є –њ—А–µ–Ј —Ж–µ–љ—В—К—А–∞ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П. –Я–Њ–і —Е–Є–њ–µ—А—А–∞–≤–љ–Є–љ–∞ —Б–µ —А–∞–Ј–±–Є—А–∞ —В–∞–Ї–Њ–≤–∞ –њ–Њ–і–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ, –Ї–Њ–µ—В–Њ –µ —Б –µ–і–Є–љ–Є—Ж–∞ –њ–Њ-–Љ–∞–ї–Ї–Њ –Њ—В –Њ–Ї–Њ–ї–љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ. –Э–∞–њ—А–Є–Љ–µ—А, –≤ –і–≤—Г–Љ–µ—А–љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ —Е–Є–њ–µ—А—А–∞–≤–љ–Є–љ–∞—В–∞ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –ї–Є–љ–Є—П, –∞ –≤ —В—А–Є–Є–Ј–Љ–µ—А–љ–Њ—В–Њ - —А–∞–≤–љ–Є–љ–∞ –Є –і—А. |
| –Т —З–µ—В–љ–Њ–Љ–µ—А–љ–Є—В–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ —Ж–µ–љ—В—А–∞–ї–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –Ј–∞–њ–∞–Ј–≤–∞¬†–Њ—А–Є–µ–љ—В–∞—Ж–Є—П—В–∞ —Б–Є, –∞ –≤ –љ–µ—З–µ—В–љ–Њ–Љ–µ—А–љ–Є—В–µ¬†- –љ–µ. –Ф–≤–µ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Є –њ—А–µ–Њ–±—А–∞–Ј—Г–≤–∞–љ–Є—П —Б —Ж–µ–љ—В—А–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П —Б–∞ —А–∞–≤–љ–Њ—Б–Є–ї–љ–Є –љ–∞ —В—А–∞–љ—Б–ї–∞—Ж–Є—П | 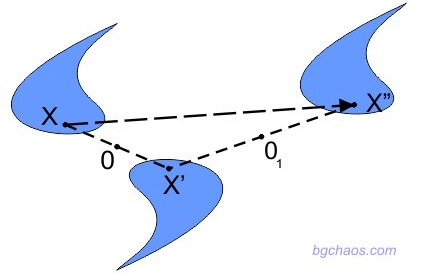 |
 –°—Е–µ–Љ–Є: bgchaos, –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ —Д–Є–≥—Г—А–Є –Њ—В Wikipedia –°—Е–µ–Љ–Є: bgchaos, –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ —Д–Є–≥—Г—А–Є –Њ—В Wikipedia |
–Т—Б–Є—З–Ї–Є –Я–ї–∞—В–Њ–љ–Њ–≤–Є —В–µ–ї–∞, —Б –Є–Ј–Ї–ї—О—З–µ–љ–Є–µ –љ–∞ —В–µ—В—А–∞–µ–і—К—А—К—В –Є–Љ–∞—В —Ж–µ–љ—В—А–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П.
–°–Є–Љ–µ—В—А–Є—П –љ–∞ —Б—Д–µ—А–∞—В–∞
–°—Д–µ—А–∞—В–∞ –Є–Љ–∞ –Є —Ж–µ–љ—В—А–∞–ї–љ–∞, –Є –Њ–≥–ї–µ–і–∞–ї–љ–∞ –Є —А–Њ—В–∞—Ж–Є–Њ–љ–љ–∞ —Б–Є–Љ–µ—В—А–Є—П. –¶–µ–љ—В—К—А—К—В –љ–∞ —Б–Є–Љ–µ—В—А–Є—П –µ –≤ —Ж–µ–љ—В—К—А–∞ –љ–∞ —Б—Д–µ—А–∞—В–∞, —А–∞–≤–љ–Є–љ–∞—В–∞ –љ–∞ –Њ–≥–ї–µ–і–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П –µ –≤—Б—П–Ї–∞ —А–∞–≤–љ–Є–љ–∞, –Љ–Є–љ–∞–≤–∞—Й–∞ –њ—А–µ–Ј —Ж–µ–љ—В—К—А–∞, –Њ—Б –љ–∞ —Б–Є–Љ–µ—В—А–Є—П - –≤—Б—П–Ї–∞ –њ—А–∞–≤–∞, –Љ–Є–љ–∞–≤–∞—Й–∞ –њ—А–µ–Ј —Ж–µ–љ—В—К—А–∞. Mo–ґ–µ –і–∞ —Б–µ —А–∞–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –µ–і–љ–∞ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–∞ –Њ—Б–µ–≤–∞ —Б–Є–Љ–µ—В—А–Є—П. –Э–µ —Б–ї—Г—З–∞–є–љ–Њ, –і—А–µ–≤–љ–Є—В–µ –≥—К—А—Ж–Є —Б–∞ —Б–Љ—П—В–∞–ї–Є –Ї—К–ї–±–Њ—В–Њ –Ј–∞ –љ–∞–є-—Б—К–≤—К—А—И–µ–љ–∞—В–∞ —Д–Њ—А–Љ–∞. –Ю–њ–Є—Б–≤–∞ —Б–µ –Њ—В –≥—А—Г–њ–∞ SO(3).
–Ы–Њ–Ї–∞–ї–љ–∞—В–∞ —Ж–µ–љ—В—А–∞–ї–љ–∞ —Б–Є–Љ–µ—В—А–Є—П –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є–ї–Є —Б—А–µ–і–∞—В–∞ —Б–µ –љ–∞—А–Є—З–∞¬†–Є–Ј–Њ—В—А–Њ–њ–Є—П. –Т—Б—П–Ї–∞ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –љ–∞ —Б–Є—Б—В–µ–Љ–∞, –Є–Љ–∞—Й–∞ —Б—Д–µ—А–Є—З–љ–∞ —Б–Є–Љ–µ—В—А–Є—П, –Ј–∞–≤–Є—Б–Є —Б–∞–Љ–Њ –Њ—В —А–∞–Ј—Б—В–Њ—П–љ–Є–µ—В–Њ –є –і–Њ —Ж–µ–љ—В—К—А–∞. –Я–Њ —Б—К—Й–Є—П—В –љ–∞—З–Є–љ —Б–Є–ї–∞—В–∞ –љ–∞ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ –њ—А–Є–≤–ї–Є—З–∞–љ–µ –Љ–µ–ґ–і—Г —В–Њ—З–Ї–Њ–≤–Є —В–µ–ї–∞ –Ј–∞–≤–Є—Б–Є —Б–∞–Љ–Њ –Њ—В —А–∞–Ј—Б—В–Њ—П–љ–Є–µ—В–Њ –Љ–µ–ґ–і—Г —В–µ–ї–∞—В–∞, –Ј–∞—В–Њ–≤–∞ —Б–µ –Ї–∞–Ј–≤–∞, —З–µ —В–∞–Ј–Є —Б–Є–ї–∞ –µ —Б—Д–µ—А–Є—З–љ–Њ —Б–Є–Љ–µ—В—А–Є—З–љ–∞.
–Ґ—А–∞–љ—Б–ї–∞—Ж–Є–Њ–љ–љ–∞ (–њ–µ—А–Є–Њ–і–Є—З–љ–∞) —Б–Є–Љ–µ—В—А–Є—П
 –У—А–∞–≤—О—А–∞ "–Ю—Б–µ–Љ –≥–ї–∞–≤–Є", M.C.Esher –У—А–∞–≤—О—А–∞ "–Ю—Б–µ–Љ –≥–ї–∞–≤–Є", M.C.Esher |
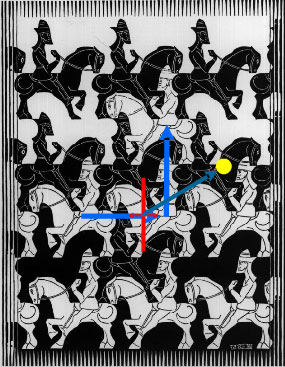
–Я—А–Є —В–Њ–Ј–Є —В–Є–њ —Б–Є–Љ–µ—В—А–Є—П –Њ–±–µ–Ї—В–Є—В–µ –Њ—Б—В–∞–≤–∞—В –љ–µ–Є–Ј–Љ–µ–љ–љ–Є –њ—А–Є –і–Є—Б–Ї—А–µ—В–љ–Є –Є–ї–Є –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Є —В—А–∞–љ—Б–ї–∞—Ж–Є–Є.¬† –Х–ї–µ–Љ–µ–љ—В–Є—В–µ –Њ—В —Б–Є—Б—В–µ–Љ–∞—В–∞ —Б–µ –њ–Њ–≤—В–∞—А—П—В –њ–Њ —Б—В—А–Њ–≥–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є –Њ—В–Љ–µ—Б—В–≤–∞–љ–Є—П. –С–µ–Ј–Ї—А–∞–є–љ–∞ —А–∞–≤–љ–Є–љ–∞ —Б–µ –њ–Њ–Ї—А–Є–≤–∞ —Д–Є–≥—Г—А–Є —Б —В—А–∞–љ—Б–ї–∞—Ж–Є–Њ–љ–љ–∞ —Б–Є–Љ–µ—В—А–Є—П –Њ—В –љ–∞—З–∞–ї–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П –њ–Њ —Д–Њ—А–Љ—Г–ї–∞—В–∞:
|
|
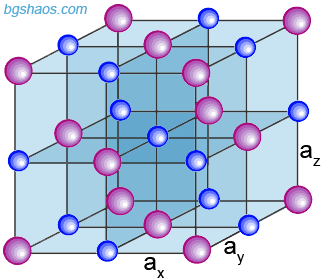
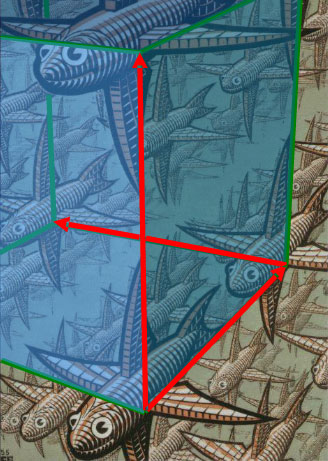
–Р—В–Њ–Љ–љ–∞—В–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –љ–∞ –Ї—А–Є—Б—В–∞–ї–Є—В–µ –Є–Љ–∞ —В—А–∞–љ—Б–ї–∞—Ж–Є–Њ–љ–љ–∞ —Б–Є–Љ–µ—В—А–Є—П. –Ґ—П —Б–µ –Њ–њ–Є—Б–≤–∞ –Ї–∞—В–Њ —Б–±–Њ—А –Њ—В –њ–Њ–≤—В–∞—А—П—Й–Є —Б–µ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –µ–і–љ–∞–Ї–≤–Є –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–Є –Ї–ї–µ—В–Ї–Є, —Б —Д–Њ—А–Љ–∞—В–∞ –љ–∞ –њ–∞—А–∞–ї–µ–ї–µ–њ–Є–њ–µ–і —Б —А—К–±–Њ–≤–µ ax, ay, az (–њ–µ—А–Є–Њ–і–Є –љ–∞ –Ї—А–Є—Б—В–∞–ї–љ–Є—В–µ —А–µ—И–µ—В–Ї–Є) |
 |
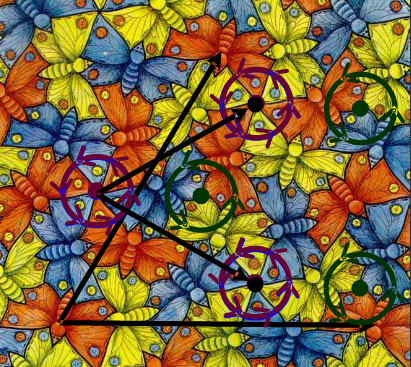
–Ґ—А–∞–љ—Б–ї–∞—Ж–Є–Њ–љ–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П –µ –≤ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –Љ–Њ–Ј–∞–є–Ї–Є—В–µ, –Ј–∞ –Ї–Њ–Є—В–Њ —Й–µ –Є–Љ–∞ –Њ—В–і–µ–ї–љ–∞ —В–µ–Љ–∞. –Р–Ї–Њ —Б–µ –≤–≥–ї–µ–і–∞–Љ–µ –≤ –њ—А–Њ—З—Г—В–Є—В–µ –Љ–Њ–Ј–∞–є–Ї–Є –љ–∞ –Х—И–µ—А —Й–µ –Ј–∞–±–µ–ї–µ–ґ–Є–Љ –Є —В—А–∞–љ—Б–ї–∞—Ж–Є–Њ–љ–љ–∞—В–∞ —Б–Є–Љ–µ—В—А–Є—П (—В—П –µ –≤ —Б–∞–Љ–Њ—В–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ –љ–∞ –њ–∞—В–µ—А–љ–∞, –Љ–Њ–Ј–∞–є–Ї–∞—В–∞) –Є –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Є –Њ—В –≤—Б–Є—З–Ї–Є –і—А—Г–≥–Є —Б–Є–Љ–µ—В—А–Є–Є:
 |  |  |
|---|---|---|
|
|
|
–Ш–ї—О—Б—В—А–∞—Ж–Є–Є: MC Escher
–Ш–Љ–∞ –Є –і—А—Г–≥–Є –≤–Є–і–Њ–≤–µ —Б–Є–Љ–µ—В—А–Є–Є, –Ї–Њ–Є—В–Њ —Б–∞ –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є–Є –Њ—В –Є–Ј–±—А–Њ–µ–љ–Є—В–µ –і–Њ—Б–µ–≥–∞ –Ї–∞—В–Њ —Б–њ–Є—А–∞–ї–Њ–≤–Є–і–љ–∞—В–∞ (—Е–µ–ї–Є–Ї–Њ–Є–і–∞–ї–љ–∞, –≤–Є–љ—В–Њ–≤–∞) —Б–Є–Љ–µ—В—А–Є—П –Є –і—А.
–Ш–Ј—В–Њ—З–љ–Є—Ж–Є:
–Я.–Я–µ–љ—З–µ–≤, –°–Є–Љ–µ—В—А–Є—П –љ–∞ –Љ–Њ–ї–µ–Ї—Г–ї–Є—В–µ. –І–∞—Б—В 1., –°–њ–Є—Б–∞–љ–Є–µ "–Ъ–Њ—Б–љ–Њ—Б", –±—А–Њ–є 2, 2006 –≥., kosnos.com
–§–Њ—А–Љ—Л –Є —Б–Є–Љ–Љ–µ—В—А–Є—П –§–Є–Ј–Є–Ї–∞ 10/6.10, –Ч–∞–Ї–Њ–љ—Л —Б–Њ—Е—А–∞–љ–µ–љ–Є—П –≤ –Љ–µ—Е–∞–љ–Є–Ї–µ
–Ч–∞–Љ–µ—В–Ї–Є –Њ —Б–Є–Љ–Љ–µ—В—А–Є–Є, –°–ї–Њ–±–Њ–і—П–љ—О–Ї –Р.–Ш.
–°–Є–Љ–Љ–µ—В—А–Є—П
–Ь–∞—А–Ї—К—Б –і—О –°–Њ—В–Њ–є: –°–Є–Љ–µ—В—А–Є—П—В–∞, –Ј–∞–≥–∞–і–Ї–∞—В–∞ –љ–∞ —А–µ–∞–ї–љ–Њ—Б—В—В–∞
–Я–Њ–≤–Њ—А–Њ—В—Л –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ-–≤—А–µ–Љ–µ–љ–Є
The art of M.C. Escher symmetry and physics


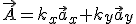 , –Ї—К–і–µ—В–Њ kx, ky –µ –Ї–Њ–µ –і–∞ –µ —Ж—П–ї–Њ —З–Є—Б–ї–Њ
, –Ї—К–і–µ—В–Њ kx, ky –µ –Ї–Њ–µ –і–∞ –µ —Ж—П–ї–Њ —З–Є—Б–ї–Њ



















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
–Э—П–Љ–∞ –Ї–Њ–Љ–µ–љ—В–∞—А–Є –Ї—К–Љ —В–∞–Ј–Є –љ–Њ–≤–Є–љ–∞ !
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
4I4ATA
–Э–Њ–≤, —Б–Ї—А–Є—В –і–Њ—Б–µ–≥–∞ –≤—Е–Њ–і –≤ –њ–Є—А–∞–Љ–Є–і–∞—В–∞ –љ–∞ –Ь–Є–Ї–µ—А–Є–љ –µ –Њ—В–Ї—А–Є—В –њ–Њ –∞–љ–Њ–Љ–∞–ї–Є–Є –њ—А–Є —Б–Ї–∞–љ–Є—А–∞–љ–µ
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews