
Кристалите около нас
Интересен е произхода на думата "кристал" - от гръцки "κρύσταλλος" - лед, дума, производна на гръцката κρύος, студ. Преди векове, сред вечните снегове на Алпите, на територията на днешна Швейцария, тогавашните "изследователи" са намирали интересни, напълно безцветни кристали, които им изглеждали като прозрачен лед. Нарекли ги "kristallos" - лед, предполагайки, че ледът като стои дълго време в планината, на студа, се вкаменява и губи способността си да се топи. Любопитно е, че същото са мислели в древни времена и в Китай и Япония - там също лед и планински кристал е една и съща дума.
 Снимка: blacktigergroup Снимка: blacktigergroup |
 Снимка: etsy.com Снимка: etsy.com |
 Снимка:scienceofsand.info Снимка:scienceofsand.info |
 Снимка: Charlene Снимка: Charlene |
В една или друга форма, кристалите са около нас ежедневно. Пишем с кристали, ядем кристали, пием кристали, перем дрехите си с кристали и се излежаваме през почивката си в кристали, но често кристалите около нас са толкова малки (защото са расли натясно), че не ги забелязваме. Обаче когато ни попадне някой по-едър екземпляр сме като омагьосани. Ако се замислите какво ни възхищава у тях - форма, прозрачност, блясък, ще разберете, че тези качества се дължат на симетрията им - външната им симетрия и вътрешната им симетрия на кристалната им решетка.
Кристалната решетка
Кристалите са еднородни твърди тела, оградени с плоски стени, които са проява на закономерния им вътрешен строеж от подредени атоми, образуващи периодична тримерна пространствена опаковка, наречена кристална решетка. Частиците - атоми, йони или молекули, които образуват пространствената кристална решетка са групирани в еднообразно ориентирани идентични една на друга елементарни клетки.
 Снимки: pramiz.com и tend2it Снимки: pramiz.com и tend2it |
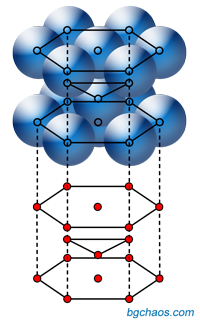
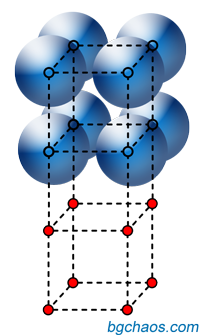
Всеки, който си е играл с магнитни топчета е усетил, че има само два начина за подреждането им стабилно: хексагонален (като пчелна пита) и кубичен.
Така е и с кристалните решетки. Всяка сфера обаче съдържа поне една частица - атом, йон или молекула.
Простите кристали са само с един атом в единичната клетка. В кристалите на неорганичните вещества могат да бъдат до 100 атома или молекули, а органичните съединения - до 100 000 атома на единичната клетка.
При кристалите, а те са съставени от повтарящи се, транслиращи се в пространството еднакви елементарни клетки, център на симетрия може да бъде всеки възел на елементарните клетки, в средата на ръбовете и центровете на страните им. Равнината на симетрия е също елемент на симетрията на кристалната решетка.
 |
 |
|
| Вляво-хексагонална (шестоъгълна), вдясно - кубична структура на кристалната решетка. Илюстрации: bgchaos, по идея на The Physical Earth (London 1977) | ||
Според принципа на суперпозиция на симетрията, наречен на името на Кюри, когато наслагваме две или повече геометрични тела, в полученото тяло остават само тези елементи на симетрия, които са общи за съставящите го тела с отчитане на взаимното разположение.
Този принцип Кюри пренася и върху физичните явления и свойства на кристалите. В този случай явленията се разглеждат от две съставни части: външното действие и средата, която се подлага на това въздействие. Външното въздействие не само обуславя симетрията на средата, но и "създава" една или друга характеристика и определя нейната симетрия.
Симетрията на външните въздействия винаги е по-висока или равна от симетрията на средата. Така например кубът (група m3m) под псевдоскаларно въздействие (група ∞ /∞ ) придобива 432 симетрия, която е по-ниска от симетрията на въздействието. Може да се случи симетрията на кристала да съвпадне с симетрията на въздействието, но никога не се случвае симетрията на кристала да е по-голяма от симетрията на въздействието. Симетрията на дадено физично свойство трябва непременно да съдържа и симетрията на причината, която го поражда.
Едни и същи кристали с различна форма
| Например елементарната клетка на кристала халит (готварска сол или натриев хлорид) е куб с осем хлорни йони (червените топчета) в ъглите и 6 в центровете на стените и 12 натриеви йони (черни топчета) в средата на ръбовете на куба и един - в центъра на куба. | 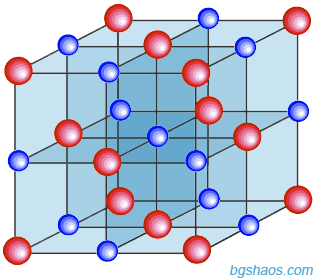 |
Външният вид на кристала отразява точно симетрията, но не винаги формата на единичната клетка. Единичната клетка на солта е във формата на куб, но кристали на солта може да са както кубични, така и други форми на същия вид симетрия като октаедъра.
 Снимка: chemistry.about.com Снимка: chemistry.about.com |
 Снимка: Arkenstone Снимка: Arkenstone |
 Снимка: wikipedia Снимка: wikipedia |
| И трите минерала горе са флуорит (CaF2) , но в различни форми, въпреки, че решетката му е една и съща. Един куб може се да модифицира, като се отсичат ъглите, а ако ги отсечем напълно, резултатът е октаедър, който се състои от малки елементарни кубчета. Как се случва това показва тази кратка анимация. |
Ледените кристали
Свободната молекула вода може да се изобрази като тетраедър, в центъра на който се намира атом кислород, а на двата върха - по един водороден атом, ковалентно свързан с кислорода. В другите два върха са разположени валентните електрони на кислорода, които не участват във вътрешномолекулните ковалентни връзки.
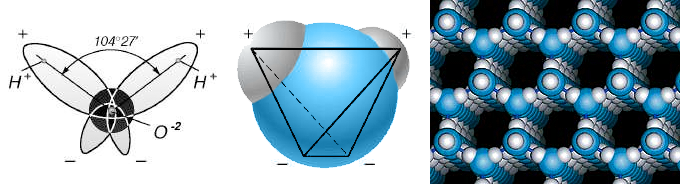 Илюстрации: сп. "В.Ю.Скосарь" Илюстрации: сп. "В.Ю.Скосарь" |
Съседните молекули си взаимодействат така: протон от една молекула се свързва с валентните електрони на друга молекула. По този начин всяка молекула може да образува четири водородни връзки със съседните молекули. Тези връзки, макар и по-слаби от вътрешномолекулните ковалентни връзки, са достатъчни, за да се образува кристал. Шестоъгълната симетрия на снежинките произхожда от кристалната решетка на леда, отразявайки вътрешното подреждане на атомите, но също като при солта и флуорита, далеч не повтаря формата на елементарната клетка.
 |
 |
 |
 |
Снимките са от сайта: SnowCrystals.com
Защо само на 6 и 4 ?
Осите могат да са оси само от 2 -, 3 -, 4 - и 6-ти порядък и оси от друг порядък са невъзможни. Защо? Възлите на кристалната решетка образуват система от правилни многоъгълници, които съвпадат един с друг при въртене на осите на симетрия без пролуки и покриват цялата повърхност.
Да разгледаме точка, в която се събират съседните ръбове на правилните многоъгълници. Ако р - броят на ръбове, които се срещат в тази точка, то ъгъла между ребрата е 2π /р, а ъгъла между страните на правилен n-ъгълник е π (n-2) /n
При запълване на равнина с правилни многоъгълници без пролуки, тези ъгли са равни:
2π /р=π (n-2) /n, можем да изведем p=2n/(n–2).
Решенията на това уравнение, при услови е, че р и n са цели числа са: n=3, n=4, n=6.
Доказахме, че други правилни многоъгълници, които без пролуки да покрият повърхност, не съществуват. Към тях единствено може да се добавят ос n=2 (огледална равнина) и n=1 (завъртане на 360°).
 |
 |
 |
Изводът е, че елементите на точковите групи симетрия в кристалните решетки имат краен брой, както и броя на възможните симетрии.
Седемте сингонии
Елементите на симетрия на кристалите са ос и равнината на центровете. Комбинацията от елементите на симетрия водят до 32 класове на симетрия, които могат да бъдат групирани в седем различни системи кристали, наречени сингонии, от гръцки σύν, "съгласно, заедно" и γωνία - "ъгъл". Има седем сингонии - триклинна, моноклинна, орторомбична, тетрагонална, тригонална, хексагонална и кубична:
Триклинна
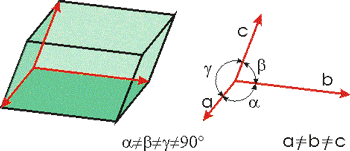 |
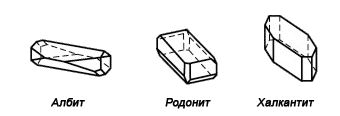 и повечето фелдшпати и глини. Симетрия на решетката по Херман-Моген: 1 (виж Симетриите като групи) и повечето фелдшпати и глини. Симетрия на решетката по Херман-Моген: 1 (виж Симетриите като групи) |
 Халкантит,liftingshadows Халкантит,liftingshadows |
 Албит, wikipedia Албит, wikipedia |
 Родонит, Arkenstone Родонит, Arkenstone |
 Кианит, crystalholistics Кианит, crystalholistics |
Моноклинна
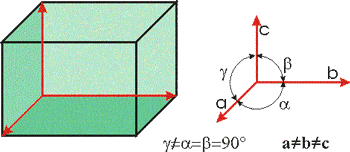 |
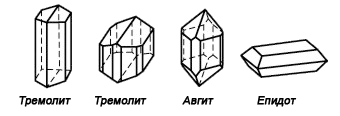 и още някои амфиболи и пироксени, гипс, захар и други. Симетрия на решетката по Херман-Моген: 2/m и още някои амфиболи и пироксени, гипс, захар и други. Симетрия на решетката по Херман-Моген: 2/m |
 Азурит, Снимка:webmineral.com Азурит, Снимка:webmineral.com |
 Тремолит, Снимка: China Neolithic Тремолит, Снимка: China Neolithic |
 Авгит, Снимка: wikipedia Авгит, Снимка: wikipedia |
 Епидот, Снимка: Greek Rocks Епидот, Снимка: Greek Rocks |
Ромбична(орторомбична)
 |
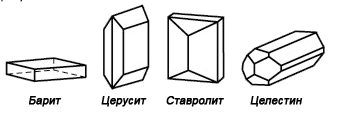 и оливин, андалузит, силиманит, някои амфиболи и пироксени, топаз, сяра и други. Симетрия на решетката по Херман-Моген: mmm и оливин, андалузит, силиманит, някои амфиболи и пироксени, топаз, сяра и други. Симетрия на решетката по Херман-Моген: mmm |
 Ставролит, Снимка:wild iris market Ставролит, Снимка:wild iris market |
 Целестин, Снимка: wisconsingeo Целестин, Снимка: wisconsingeo |
 Пироксен, Снимка: China Neolithic Пироксен, Снимка: China Neolithic |
 Андалузит, Снимка: und.nodak.edu Андалузит, Снимка: und.nodak.edu |
Тетрагонална
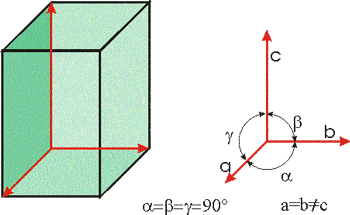 |
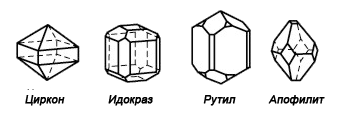 и вулфенит, каситерит и халкопирит и други. Симетрия на решетката по Херман-Моген: 4/mmm и вулфенит, каситерит и халкопирит и други. Симетрия на решетката по Херман-Моген: 4/mmm |
 Циркон, Снимка: Arkenstone Циркон, Снимка: Arkenstone |
 Рутил, Снимка: Arkenstone Рутил, Снимка: Arkenstone |
 Каситерит, Снимка: crystal habits Каситерит, Снимка: crystal habits |
 Вулфенит, Снимка: tumblr.com Вулфенит, Снимка: tumblr.com |
Тригонална
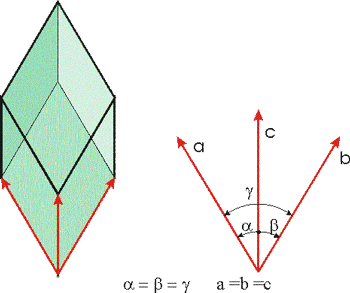 |
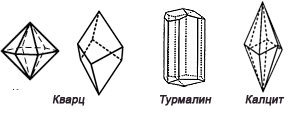 и ярозит, доломит, цинобър, турмалин, антимон, хематит, корунд и други. Симетрия на решетката по Херман-Моген: 3m и ярозит, доломит, цинобър, турмалин, антимон, хематит, корунд и други. Симетрия на решетката по Херман-Моген: 3m |
 Кварц, Снимка:tumblr.com Кварц, Снимка:tumblr.com |
 Турмалин, Снимка: customgemstones Турмалин, Снимка: customgemstones |
 Доломит, Снимка: Dennis Tasa Доломит, Снимка: Dennis Tasa |
 Цинобър, Снимка: mindat.org Цинобър, Снимка: mindat.org |
Хексагонална
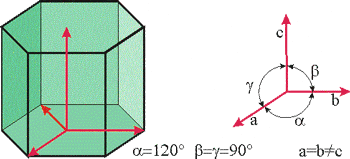 |
 ванадинит, лед и други. Симетрия на решетката по Херман-Моген: 6/mmm ванадинит, лед и други. Симетрия на решетката по Херман-Моген: 6/mmm |
 Апатит, Мineral Мasterpiece Апатит, Мineral Мasterpiece |
 Берил, Снимка: wikimedia Берил, Снимка: wikimedia |
 Greenockite, Снимка: China Neolithic Greenockite, Снимка: China Neolithic |
 Ванадинит, Снимка: FineMineralBlog Ванадинит, Снимка: FineMineralBlog |
Кубична
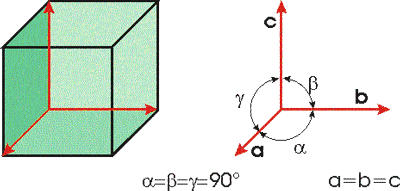 |
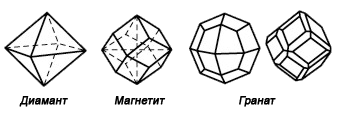 флуорит, галенит, сфалерит и други. Симетрия на решетката по Херман-Моген: mЗm флуорит, галенит, сфалерит и други. Симетрия на решетката по Херман-Моген: mЗm |
 Флуорит, Снимка: geology1403 Флуорит, Снимка: geology1403 |
 Гранат, Снимка: China Neolithic Гранат, Снимка: China Neolithic |
 Галенит, Снимка: jmu.edu Галенит, Снимка: jmu.edu |
 Диамант, Снимка: open.ac.uk Диамант, Снимка: open.ac.uk |
Много от тези камъчета в миналото са карали някои мъже да се хващат за сабята или да предприемат дълги и опасни пътешествия с несигурни корабчета.
Днес притегателната им сила не е намаляла - хората инвестират, колекционират, а някои се лекуват и медитират с тях. И макар да сме свикнали под "кристали" да разбираме именно тези "скъпоценни" камъчета, от кристали се състои почти цялата земна кора, заедно с ледените шапки.
Специално за мразещите математиката, искам да подчертая, че именно симетрията, тоест математиката е тази, която ги е направила красиви за нас.
Всъщност малко несправедливо съм нарекла кристалите "тържеството на симетрията", защото газовете, течностите и аморфните тела имат симетрия от по-висш порядък. Хаосът, в който се намират техните молекули ги прави хомогенни и изотропни, техните свойства са еднакви навсякъде и във всички посоки, за разлика от кристалите.
Разбрахме, че при кристалите се наблюдава осева симетрия само от 1, 2, 3, 4 и 6-ти ред.
Няма кристални решетки със симетрия от 5-ти ред.
В следващата публикация ще видим, че този "пропуснат" порядък се появява в животинския свят като едни от най-развитите безгръбначни и братовчеди на първите гръбначни организми, бодлокожите (морски звезди и таралежи) притежават симетрия от 5-ти порядък.
Източници:
Основи на минералогията, Руслан Иванов Костов
Кристализация от разтвори, Николай Теодосиев
Форма и строение кристаллов Solids, Liquids and Solutions, ChemPaths
Junior Science - Crystals КРИСТАЛЛЫ, krugosvet.ru
The Fascinating World of Minerals, Mineralogical Association of Canada
Загадка воды. Кристаллы льда, снежинки Crystal habit, wikipedia
Основы физики твердых тел, Уральский федеральный университет
Электрические свойства кристаллов, Горяева А
Hermann-Mauguin notation, wikipedia
Кристаллы, Химическая энциклопедия П.Пенчев, Симетрия на молекулите. Част 1., Списание "Коснос", брой 2, 2006 г.,kosnos.com
External Symmetry of Crystals, 32 Crystal Classes, Prof. Stephen A. Nelson
Teaching crystallographic and magnetic point group symmetry using three-dimensional rendered visualizations, Marc De Graef
СИММЕТРИЯ МОЛЕКУЛ И КРИСТАЛЛИЧЕСКИХ СТРУКТУР, М. А. Порай-Кошица




















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон
dolivo
Сахара очаква 75% увеличение на валежите до 2100 г.
dolivo
Земната ябълка: стара култура за новите климатични времена