

–½–Α –Ψ–Ω–Η―¹–Α–Ϋ–Η–Β –Ϋ–Α –£―¹–Β–Μ–Β–Ϋ–Α―²–Α –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ –Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Β–¥–Ϋ–Ψ –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Β –Ω–Ψ-–Φ–Α–Μ–Κ–Ψ, –Ψ―²–Κ–Ψ–Μ–Κ–Ψ―²–Ψ ―¹–Β ―¹–Φ―è―²–Α, ―΅–Β ―²―è –Ω―Ä–Η―²–Β–Ε–Α–≤–Α. –‰–Ζ―΅–Η―¹–Μ–Β–Ϋ–Η―è –Ϋ–Α –Δ–Θ –£–Η–Β–Ϋ–Α –Ω–Ψ–Κ–Α–Ζ–≤–Α―², ―΅–Β –Ϋ–Β ―¹―²–Α–≤–Α –≤―ä–Ω―Ä–Ψ―¹ –Ω―Ä–Ψ―¹―²–Ψ –Ζ–Α –Ϋ―è–Κ–Α–Κ―ä–≤ ―²―Ä–Η–Κ –Ϋ–Α –Η–Ζ―΅–Η―¹–Μ–Β–Ϋ–Η–Β, –Α –Ζ–Α –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Ψ ―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Ϋ–Α –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ―²–Ψ.
–ù–Α –Ω―Ä―ä–≤ –Ω–Ψ–≥–Μ–Β–¥ –Η–Ζ–≥–Μ–Β–Ε–¥–Α –≤―¹―è–Κ–Ψ ―¹―ä–Φ–Ϋ–Β–Ϋ–Η–Β –Β –Η–Ζ–Κ–Μ―é―΅–Β–Ϋ–Ψ: –½–Α –Ϋ–Α―¹ –£―¹–Β–Μ–Β–Ϋ–Α―²–Α –Β ―²―Ä–Η–Η–Ζ–Φ–Β―Ä–Ϋ–Α. –ï–¥–Ϋ–Α –Ψ―² –Ϋ–Α–Ι-―¹―²―Ä–Α―Ö–Ψ–≤–Η―²–Η―²–Β –Η–¥–Β–Η –Ϋ–Α ―²–Β–Ψ―Ä–Β―²–Η―΅–Ϋ–Α―²–Α ―³–Η–Ζ–Η–Κ–Α –Ω―Ä–Β–Ζ –Ω–Ψ―¹–Μ–Β–¥–Ϋ–Η―²–Β –¥–≤–Β –¥–Β―¹–Β―²–Η–Μ–Β―²–Η―è –Ψ–±–Α―΅–Β –Ω–Ψ―¹―²–Α–≤―è –Ω–Ψ–¥ ―¹―ä–Φ–Ϋ–Β–Ϋ–Η–Β –Η–Φ–Β–Ϋ–Ϋ–Ψ ―²–Ψ–≤–Α: βÄû–ü―Ä–Η–Ϋ―Ü–Η–Ω―ä―² –Ϋ–Α ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³–Η―è―²–ΑβÄ€ –Κ–Α–Ζ–≤–Α, ―΅–Β –Ζ–Α –Ψ–Ω–Η―¹–Α–Ϋ–Η–Β –Ϋ–Α –Ϋ–Α―à–Α―²–Α –£―¹–Β–Μ–Β–Ϋ–Α –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ –Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Β–¥–Ϋ–Ψ –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Β –Ω–Ψ-–Φ–Α–Μ–Κ–Ψ, –Ψ―²–Κ–Ψ–Μ–Κ–Ψ―²–Ψ ―¹–Β ―¹–Φ―è―²–Α, ―΅–Β ―²―è –Ω―Ä–Η―²–Β–Ε–Α–≤–Α. –Δ–Ψ–≤–Α, –Κ–Ψ–Β―²–Ψ –Ϋ–Η–Β –≤―ä–Ζ–Ω―Ä–Η–Β–Φ–Α–Φ–Β –Κ–Α―²–Ψ ―²―Ä–Η–Η–Ζ–Φ–Β―Ä–Ϋ–Ψ, –Φ–Ψ–Ε–Β –¥–Α ―¹–Β ―Ä–Α–Ζ–≥–Μ–Β–Ε–¥–Α –Ψ―â–Β –Κ–Α―²–Ψ –Η–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Β –Ϋ–Α –¥–≤―É–Η–Ζ–Φ–Β―Ä–Ϋ–Η –Ω―Ä–Ψ―Ü–Β―¹–Η –Ϋ–Α ―³–Ψ–Ϋ–Α –Ϋ–Α –Ψ–≥―Ä–Ψ–Φ–Ϋ–Η―è –Κ–Ψ―¹–Φ–Η―΅–Β―¹–Κ–Η ―Ö–Ψ―Ä–Η–Ζ–Ψ–Ϋ―².
–î–Ψ―¹–Β–≥–Α ―¹–Α –Ω―Ä–Α–≤–Β–Ϋ–Η –Ω―Ä–Ψ―É―΅–≤–Α–Ϋ–Η―è ―¹–Α–Φ–Ψ –≤ –Β–¥–Ϋ–Ψ –Β–Κ–Ζ–Ψ―²–Η―΅–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ-–≤―Ä–Β–Φ–Β ―¹ –Ψ―²―Ä–Η―Ü–Α―²–Β–Μ–Ϋ–Ψ –Η–Ζ–Κ―Ä–Η–≤―è–≤–Α–Ϋ–Β, –Κ–Ψ–Β―²–Ψ –Ψ―² ―²–Β–Ψ―Ä–Β―²–Η―΅–Ϋ–Α –≥–Μ–Β–¥–Ϋ–Α ―²–Ψ―΅–Κ–Α –¥–Β–Ι―¹―²–≤–Η―²–Β–Μ–Ϋ–Ψ –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–≤–Α –Η–Ϋ―²–Β―Ä–Β―¹, –Ϋ–Ψ ―¹–Β ―Ä–Α–Ζ–Μ–Η―΅–Α–≤–Α –Ζ–Ϋ–Α―΅–Η―²–Β–Μ–Ϋ–Ψ –Ψ―² –Ϋ–Α―à–Α―²–Α –£―¹–Β–Μ–Β–Ϋ–Α. –†–Β–Ζ―É–Μ―²–Α―²–Η –Ψ―² –Ω―Ä–Ψ―É―΅–≤–Α–Ϋ–Η―è –Ϋ–Α –Δ–Θ –£–Η–Β–Ϋ–Α ―¹–Β –¥–Ψ–±–Μ–Η–Ε–Α–≤–Α―² –¥–Ψ –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β―²–Ψ, ―΅–Β ―²–Ψ–Ζ–Η ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η –Ω―Ä–Η–Ϋ―Ü–Η–Ω –Β –≤ ―¹–Η–Μ–Α –Η –Ζ–Α –Ω–Μ–Ψ―¹–Κ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ-–≤―Ä–Β–Φ–Β, ―²–Α–Κ–Ψ–≤–Α, –Κ–Α–Κ–≤–Ψ―²–Ψ –≥–Ψ –Ϋ–Α–±–Μ―é–¥–Α–≤–Α–Φ–Β –Ϋ–Η–Β –≤ –Ϋ–Α―à–Α―²–Α –£―¹–Β–Μ–Β–Ϋ–Α.
–Ξ–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η―è―² –Ω―Ä–Η–Ϋ―Ü–Η–Ω
 –Ξ–Ψ–Μ–Ψ–≥―Ä–Α–Φ–Α, ―Ä–Α–±–Ψ―²–Α –Ϋ–Α –¥–Η–Ζ–Α–Ι–Ϋ–Β―Ä–Α¬†Oliver Laric –Ξ–Ψ–Μ–Ψ–≥―Ä–Α–Φ–Α, ―Ä–Α–±–Ψ―²–Α –Ϋ–Α –¥–Η–Ζ–Α–Ι–Ϋ–Β―Ä–Α¬†Oliver Laric |
–Ξ–Ψ–Μ–Ψ–≥―Ä–Α–Φ–Η―²–Β ―¹–Α –Ϋ–Η –Ω–Ψ–Ζ–Ϋ–Α―²–Η –Ψ―² –±–Α–Ϋ–Κ–Ϋ–Ψ―²–Η –Η–Μ–Η –Κ―Ä–Β–¥–Η―²–Ϋ–Η –Κ–Α―Ä―²–Η. –Δ–Β –≤―¹―ä―â–Ϋ–Ψ―¹―² ―¹–Α –¥–≤―É–Η–Ζ–Φ–Β―Ä–Ϋ–Η, –Ϋ–Η–Β –Ψ–±–Α―΅–Β –≥–Η –≤–Η–Ε–¥–Α–Φ–Β –Κ–Α―²–Ψ ―²―Ä–Η–Η–Ζ–Φ–Β―Ä–Ϋ–Η. –‰–Φ–Α –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ―¹―² –Ω–Ψ–≤–Β–¥–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α –£―¹–Β–Μ–Β–Ϋ–Α―²–Α –¥–Α –Β –Ω–Ψ–¥–Ψ–±–Ϋ–Ψ.
–Γ–Ω–Ψ―Ä–Β–¥ ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η―è –Ω―Ä–Η–Ϋ―Ü–Η–Ω, –Ζ–Α –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Ψ―²–Ψ –Ψ–Ω–Η―¹–Α–Ϋ–Η–Β –Ϋ–Α –£―¹–Β–Μ–Β–Ϋ–Α―²–Α –Β –¥–Ψ―¹―²–Α―²―ä―΅–Ϋ–Α –Η–Ϋ―³–Ψ―Ä–Φ–Α―Ü–Η―è―²–Α, ―¹―ä–¥―ä―Ä–Ε–Α―â–Α ―¹–Β –≤―ä–≤ –≤―ä–Ϋ―à–Ϋ–Α―²–Α –Ι –≥―Ä–Α–Ϋ–Η―Ü–Α.
βÄû–û―â–Β –Ω―Ä–Β–Ζ 1997 ―³–Η–Ζ–Η–Κ―ä―² –Ξ―É–Α–Ϋ –€–Α–Μ–¥–Α―¹–Β–Ϋ–Α –Η–Ζ–Κ–Α–Ζ–≤–Α –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β―²–Ψ, ―΅–Β –Β –Ϋ–Α–Μ–Η―Ü–Β ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É ―²–Β–Ψ―Ä–Η–Η―²–Β –Ϋ–Α –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è―²–Α –≤ –Η–Ζ–Κ―Ä–Η–≤–Β–Ϋ–Η –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α –Η –Κ–≤–Α–Ϋ―²–Ψ–≤–Η―²–Β ―²–Β–Ψ―Ä–Η–Η –Ϋ–Α –Ω–Ψ–Μ–Β―²–Ψ –≤ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α ―¹ –Β–¥–Ϋ–Ψ –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η–Β –Ω–Ψ-–Φ–Α–Μ–Κ–ΨβÄ€, –Κ–Α–Ζ–≤–Α –î–Α–Ϋ–Η–Β–Μ –™―Ä―É–Φ–Η–Μ–Β―Ä –Ψ―² –‰–Ϋ―¹―²–Η―²―É―²–Α –Ζ–Α ―²–Β–Ψ―Ä–Β―²–Η―΅–Ϋ–Α ―³–Η–Ζ–Η–Κ–Α –Κ―ä–Φ –Δ–Β―Ö–Ϋ–Η―΅–Β―¹–Κ–Η ―É–Ϋ–Η–≤–Β―Ä―¹–Η―²–Β―² –£–Η–Β–Ϋ–Α.
–™―Ä–Α–≤–Η―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Η―²–Β ―è–≤–Μ–Β–Ϋ–Η―è ―¹–Α –Ψ–Ω–Η―¹–Α–Ϋ–Η –≤ ―²–Β–Ψ―Ä–Η―è ―¹ ―²―Ä–Η –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Η –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è (–û–Δ–û), –Ω–Ψ–≤–Β–¥–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α –Κ–≤–Α–Ϋ―²–Ψ–≤–Η―²–Β ―΅–Α―¹―²–Η―Ü–Η ―¹–Β –Η–Ζ―΅–Η―¹–Μ―è–≤–Α―² –Ω–Ψ ―²–Β–Ψ―Ä–Η―è ―¹–Α–Φ–Ψ ―¹ –¥–≤–Β –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Η –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è.
–Γ–Ω–Ψ―Ä–Β–¥ ―Ö–Ψ–Μ–Ψ–≥―Ä–Α–Φ–Ϋ–Η―è―² –Ω―Ä–Η–Ϋ―Ü–Η–Ω –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ψ–±–Β–¥–Η–Ϋ―è―² ―Ä–Β–Ζ―É–Μ―²–Α―²–Η―²–Β –Ψ―² –¥–≤–Β―²–Β ―²–Β–Ψ―Ä–Η–Η.
–ü–Ψ–¥–Ψ–±–Ϋ–Α –≤―Ä―ä–Ζ–Κ–Α –Ω―ä―Ä–≤–Ψ–Ϋ–Α―΅–Α–Μ–Ϋ–Ψ –Η–Ζ–≥–Μ–Β–Ε–¥–Α –Η–Ζ–Ϋ–Β–Ϋ–Α–¥–≤–Α―â–Α βÄ™ –≤―¹–Β –Β–¥–Ϋ–Ψ –¥–Α ―Ä–Β–Φ–Ψ–Ϋ―²–Η―Ä–Α―à CD-–Ω–Μ–Β–Ι―ä―Ä, –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Ι–Κ–Η ―³–Ψ―Ä–Φ―É–Μ–Η―²–Β –Ψ―² ―É―΅–Β–±–Ϋ–Η–Κ –Ω–Ψ –Α―¹―²―Ä–Ψ–Ϋ–Ψ–Φ–Η―è. –€–Β―²–Ψ–¥―ä―² –Ψ–±–Α―΅–Β –≤–Β―΅–Β –Β –¥–Ψ–Ϋ–Β―¹―ä–Μ ―É―¹–Ω–Β―Ö–Η. –€–Β–Ε–¥―É–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Ψ ―¹–Α –Ω―É–±–Μ–Η–Κ―É–≤–Α–Ϋ–Η –Ω–Ψ–≤–Β―΅–Β –Ψ―² 10 000 –Ϋ–Α―É―΅–Ϋ–Η ―²―Ä―É–¥–Α –≤―ä–≤ –≤―Ä―ä–Ζ–Κ–Α ―¹ –Ψ–Ω–Η―¹–Α–Ϋ–Ψ―²–Ψ –Ψ―² –€–Α–Μ–¥–Α―¹–Β–Ϋ–Α ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α―²–Α –Η –Κ–≤–Α–Ϋ―²–Ψ–≤–Α―²–Α ―²–Β–Ψ―Ä–Η―è –Ϋ–Α –Ω–Ψ–Μ–Β―²–Ψ.
–ö–Α–Κ–≤–Ψ –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α –≤―¹–Η―΅–Κ–Ψ ―²–Ψ–≤–Α - –¥–Β –Γ–Η―²–Β―Ä, –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α –Η –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α –Ω–Μ–Ψ―¹–Κ–Η, ―¹ –Ω–Ψ–Μ–Ψ–Ε–Η―²–Β–Μ–Ϋ–Α¬†–Η ―¹ –Ψ―²―Ä–Η―Ü–Α―²–Β–Μ–Ϋ–Α –Κ―Ä–Η–≤–Η–Ϋ–Α - –Ω―Ä–Ψ―΅–Β―²–Β―²–Β –≤ ―¹―²–Α―²–Η―è―²–Α –Ϋ–Α –Ξ―É–Α–Ϋ –€–Α–Μ–¥–Α―¹–Β–Ϋ–Α "–‰–Μ―é–Ζ–Η―è―²–Α –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è".
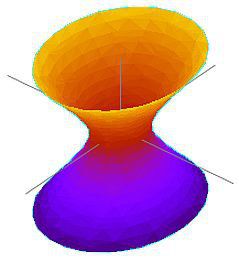 –‰–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Β –Ϋ–Α –¥–≤―É–Φ–Β―Ä–Ϋ–Ψ –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ, –≤–≥―Ä–Α–¥–Β–Ϋ–Ψ –≤ –Ω–Μ–Ψ―¹–Κ–Ψ ―²―Ä–Η–Φ–Β―Ä–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ. –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è:¬†wikipedia –‰–Ζ–Ψ–±―Ä–Α–Ε–Β–Ϋ–Η–Β –Ϋ–Α –¥–≤―É–Φ–Β―Ä–Ϋ–Ψ –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ, –≤–≥―Ä–Α–¥–Β–Ϋ–Ψ –≤ –Ω–Μ–Ψ―¹–Κ–Ψ ―²―Ä–Η–Φ–Β―Ä–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ. –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è:¬†wikipedia |
–€–Α–Μ–Κ–Ψ –Η―¹―²–Ψ―Ä–Η―è
–ü―Ä–Β–Ζ 1993 –≥. –Η–Ζ–≤–Β―¹―²–Ϋ–Η―è―² ―Ö–Ψ–Μ–Α–Ϋ–¥―¹–Κ–Η ―³–Η–Ζ–Η–Κ ―²–Β–Ψ―Ä–Β―²–Η–Κ –™–Β―Ä–Α―Ä–¥'―² –Ξ–Ψ–Ψ―³―² (Gerard't Hooft )¬† –Ω―Ä–Β–¥―¹―²–Α–≤―è ―¹–Φ–Β–Μ–Ψ –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β, –Κ–Ψ–Β―²–Ψ –Ω―Ä–Η–Μ–Η―΅–Α –Ϋ–Α –Α–Μ–Β–≥–Ψ―Ä–Η―è―²–Α –Ϋ–Α –Ω–Β―â–Β―Ä–Α―²–Α –Ϋ–Α –ü–Μ–Α―²–Ψ–Ϋ. –Δ–Ψ–≤–Α –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β, –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ –Κ–Α―²–Ψ ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η –Ω―Ä–Η–Ϋ―Ü–Η–Ω, ―¹–Β ―¹―ä―¹―²–Ψ–Η –Ψ―² –¥–≤–Β –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Η ―²–≤―ä―Ä–¥–Β–Ϋ–Η―è:
–Δ–≤―ä―Ä–¥–Β–Ϋ–Η–Β¬†1. –ü―ä―Ä–≤–Ψ―²–Ψ ―²–≤―ä―Ä–¥–Β–Ϋ–Η–Β –Ϋ–Α ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η―è –Ω―Ä–Η–Ϋ―Ü–Η–Ω –Β, ―΅–Β ―Ü―è–Μ–Α―²–Α –Η–Ϋ―³–Ψ―Ä–Φ–Α―Ü–Η―è, –Κ–Ψ―è―²–Ψ ―¹–Β ―¹―ä–¥―ä―Ä–Ε–Α –≤ –Ϋ―è–Κ–Α–Κ–≤–Α¬†–Ψ–±–Μ–Α―¹―² –Ϋ–Α –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ―²–Ψ –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ω―Ä–Β–¥―¹―²–Α–≤–Η –Κ–Α―²–Ψ "―Ö–Ψ–Μ–Ψ–≥―Ä–Α–Φ–Α", –Κ–Ψ―è―²–Ψ "―¹–Β –Η–Ζ–Μ―ä―΅–≤–Α" –Ψ―² –≥―Ä–Α–Ϋ–Η―Ü–Α―²–Α –Ϋ–Α ―²–Α–Ζ–Η –Ψ–±–Μ–Α―¹―² –Η–Μ–Η –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ–Η –Ψ―² ―²–Β–Ψ―Ä–Η―è―²–Α –Ϋ–Α –≥―Ä–Α–Ϋ–Η―Ü–Α―²–Α –Ϋ–Α ―²–Α–Ζ–Η –Ψ–±–Μ–Α―¹―².
–ù–Α–Ω―Ä–Η–Φ–Β―Ä, –Α–Κ–Ψ ―Ä–Α–Ζ–≥–Μ–Β–Ε–¥–Α–Ϋ–Α―²–Α –Ψ–±–Μ–Α―¹―² –Β ―¹–Μ–Α–¥–Κ–Α―Ä–Ϋ–Η―Ü–Α, ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η―è―² –Ω―Ä–Η–Ϋ―Ü–Η–Ω ―²–≤―ä―Ä–¥–Η, ―΅–Β ―Ü―è–Μ–Α―²–Α ―³–Η–Ζ–Η–Κ–Α –≤ ―¹–Μ–Α–¥–Κ–Α―Ä–Ϋ–Η―Ü–Α―²–Α –Φ–Ψ–Ε–Β –¥–Α –±―ä–¥–Β –Ω―Ä–Β–¥―¹―²–Α–≤–Β–Ϋ–Α –Ψ―² ―²–Β–Ψ―Ä–Η―è, –Κ–Ψ―è―²–Ψ ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ―è –Ω–Ψ ―¹―²–Β–Ϋ–Η―²–Β –Ϋ–Α ―¹–Μ–Α–¥–Κ–Α―Ä–Ϋ–Η―Ü–Α―²–Α.
–Δ–≤―ä―Ä–¥–Β–Ϋ–Η–Β 2. –£―²–Ψ―Ä–Ψ―²–Ψ ―²–≤―ä―Ä–¥–Β–Ϋ–Η–Β –Ϋ–Α ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η―è –Ω―Ä–Η–Ϋ―Ü–Η–Ω –Β, ―΅–Β ―²–Β–Ψ―Ä–Η―è―²–Α –Ϋ–Α –≥―Ä–Α–Ϋ–Η―Ü–Α―²–Α –Ϋ–Α –Η–Ζ―¹–Μ–Β–¥–≤–Α–Ϋ–Α―²–Α –Ψ–±–Μ–Α―¹―²¬†–Ϋ–Α –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ―²–Ψ ―²―Ä―è–±–≤–Α –¥–Α ―¹―ä–¥―ä―Ä–Ε–Α –Ϋ–Α–Ι-–Φ–Ϋ–Ψ–≥–Ψ –Β–¥–Ϋ–Α ―¹―²–Β–Ω–Β–Ϋ –Ϋ–Α ―¹–≤–Ψ–±–Ψ–¥–Α –Ϋ–Α –Η–Ζ–Κ–Μ―é―΅–Η―²–Β–Μ–Ϋ–Ψ –Φ–Α–Μ–Κ–Α –Ω–Μ–Ψ―â (–ü–Μ–Α–Ϋ–Κ–Ψ–≤a –Ω–Μ–Ψ―â), –Ψ–≥―Ä–Α–¥–Β–Ϋ–Α ―¹―ä―¹ ―¹―²―Ä–Α–Ϋ–Α ―¹¬†–¥―ä–Μ–Ε–Η–Ϋ–Α ―Ä–Α–≤–Ϋ–Α –Ϋ–Α –¥―ä–Μ–Ε–Η–Ϋ–Α―²–Α –Ϋ–Α –ü–Μ–Α–Ϋ–Κ, –Κ–Ψ―è―²–Ψ –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ψ ―¹–Β –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α –Κ–Α―²–Ψ Lp.
Lp = 1.6 * 10-33 ―¹–Φ
–ü―Ä–Β–Ζ 1993 –≥. ―Ö–Ψ–Μ–Α–Ϋ–¥―¹–Κ–Η―è―² ―³–Η–Ζ–Η–Κ –™–Β―Ä–Α―Ä–¥'―² –Ξ–Ψ–Ψ―³―² (Gerard't Hooft )¬†–Ω―Ä–Β–¥–Μ–Ψ–Ε–Η–Μ¬†―²–Ψ–Ζ–Η –Ω―Ä–Η–Ϋ―Ü–Η–Ω, –Κ–Α―²–Ψ –≥–Ψ¬†–Ω―Ä–Η–Μ–Α–≥–Α –Κ―ä–Φ ―¹―²―Ä―É–Ϋ–Ϋ–Α―²–Α ―²–Β–Ψ―Ä–Η―è –Ω–Ψ–¥ ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α¬†―². –Ϋ–Α―Ä. AdS/CFT-―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β.
–€–Β–Ε–¥―É–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ―²–Ψ –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Η–Φ–Α –Ψ―²―Ä–Η―Ü–Α―²–Β–Μ–Ϋ–Α –Κ―Ä–Η–≤–Η–Ϋ–Α, –Α –Κ―Ä–Η–≤–Η–Ϋ–Α―²–Α –Ϋ–Α –£―¹–Β–Μ–Β–Ϋ–Α―²–Α ―¹–Β ―¹–Φ―è―²–Α –Ζ–Α –±–Μ–Η–Ζ–Ψ –¥–Ψ –Ϋ―É–Μ–Α―²–Α, ―².–Β. ―²―è –Β –Ω–Μ–Ψ―¹–Κ–Α¬†–Η–Μ–Η –Ω–Ψ–Ϋ–Β βÄ™ –Ω–Ψ―΅―²–Η –Ω–Μ–Ψ―¹–Κ–Α. –ê –Κ–Α–Κ―²–Ψ –Ω–Ψ–Κ–Α–Ζ–≤–Α―²¬†–Η–Ζ―΅–Η―¹–Μ–Β–Ϋ–Η―è―²–Α –Ϋ–Α –Η–Ζ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ–Η―²–Β –Α–Ϋ–Α–Μ–Ψ–≥ –Ϋ–Α ―²–Ψ–≤–Α ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –Φ–Ψ–Ε–Β –¥–Α –≤–Α–Ε–Η –Η –Ζ–Α –Ω–Μ–Ψ―¹–Κ–Α –£―¹–Β–Μ–Β–Ϋ–Α.
–ü―Ä–Η–Ϋ―Ü–Η–Ω―ä―² –Ϋ–Α ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –≤ –Ω–Μ–Ψ―¹–Κ–Α –£―¹–Β–Μ–Β–Ϋ–Α
–½–Α ―²–Β–Ψ―Ä–Β―²–Η―΅–Ϋ–Α―²–Α ―³–Η–Ζ–Η–Κ–Α ―²–Ψ–Ι –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Ψ –Β –≤–Α–Ε–Β–Ϋ, –Ϋ–Ψ –Κ―ä–Φ –Ϋ–Α―¹―²–Ψ―è―â–Η―è –Φ–Ψ–Φ–Β–Ϋ―² –Ϋ–Α―à–Α―²–Α –£―¹–Β–Μ–Β–Ϋ–Α –Ϋ―è–Φ–Α –Ϋ–Η―â–Ψ –Ψ–±―â–Ψ ―¹ –Ϋ–Β–≥–Ψ. –£ –Κ―Ä–Α–Ι–Ϋ–Α ―¹–Φ–Β―²–Κ–Α –Ϋ–Η–Β –Ϋ–Β –Ε–Η–≤–Β–Β–Φ –≤ –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ. –ü–Ψ–¥–Ψ–±–Ϋ–Η –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α ―¹–Β –Ψ―²–Μ–Η―΅–Α–≤–Α―² ―¹ –Ϋ–Β–≤–Β―Ä–Ψ―è―²–Ϋ–Η ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η―¹―²–Η–Κ–Η. –Δ–Β –Η–Φ–Α―² –Ψ―²―Ä–Η―Ü–Α―²–Β–Μ–Ϋ–Ψ –Η–Ζ–Κ―Ä–Η–≤―è–≤–Α–Ϋ–Β –Η –Ψ–±–Β–Κ―²–Η, ―Ö–≤―ä―Ä–Μ–Β–Ϋ–Η –Ϋ–Α–¥–Α–Μ–Β―΅ –≤ –Ω―Ä–Α–≤–Α –Μ–Η–Ϋ–Η―è, ―¹–Β –≤―Ä―ä―â–Α―² –Ψ–±―Ä–Α―²–Ϋ–Ψ. βÄû–½–Α ―Ä–Α–Ζ–Μ–Η–Κ–Α –Ψ―² ―²―è―Ö –Ϋ–Α―à–Α―²–Α –£―¹–Β–Μ–Β–Ϋ–Α –Β ―¹―Ä–Α–≤–Ϋ–Η―²–Β–Μ–Ϋ–Ψ –Ω–Μ–Ψ―¹–Κ–Α βÄ™ –Η ―Ä–Α–Ζ–≥–Μ–Β–Ε–¥–Α–Ϋ–Α –Ψ―² –Α―¹―²―Ä–Ψ–Ϋ–Ψ–Φ–Η―΅–Β―¹–Κ–Η ―Ä–Α–Ζ―¹―²–Ψ―è–Ϋ–Η―è –Ϋ–Β–Ι–Ϋ–Ψ―²–Ψ –Η–Ζ–Κ―Ä–Η–≤―è–≤–Α–Ϋ–Β –Β –Ω–Ψ–Μ–Ψ–Ε–Η―²–Β–Μ–Ϋ–ΨβÄ€, ―¹–Ω–Ψ–¥–Β–Μ―è –î–Α–Ϋ–Η–Β–Μ –™―Ä―É–Φ–Η–Μ–Β―Ä.
–™―Ä―É–Φ–Η–Μ–Β―Ä –≤–Ω―Ä–Ψ―΅–Β–Φ –Ψ―â–Β –Ω―Ä–Β–¥–Η –Ϋ―è–Κ–Ψ–Μ–Κ–Ψ –≥–Ψ–¥–Η–Ϋ–Η –Ω―Ä–Β–¥–Ω–Ψ–Μ–Α–≥–Α, ―΅–Β –Ω―Ä–Η–Ϋ―Ü–Η–Ω―ä―² –Ϋ–Α ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β¬†–Φ–Ψ–Ε–Β –±–Η –≤–Α–Ε–Η –Η –Ζ–Α –Ϋ–Α―à–Α―²–Α ―Ä–Β–Α–Μ–Ϋ–Α –£―¹–Β–Μ–Β–Ϋ–Α. –½–Α –¥–Α ―¹–Β ―Ä–Α–Ζ–±–Β―Ä–Β ―²–Ψ–≤–Α, –Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –¥–Α ―¹–Β –Κ–Ψ–Ϋ―¹―²―Ä―É–Η―Ä–Α―² –≥―Ä–Α–≤–Η―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Η ―²–Β–Ψ―Ä–Η–Η, –Κ–Ψ–Η―²–Ψ –Ϋ―è–Φ–Α―² –Ϋ―É–Ε–¥–Α –Ψ―² –Α–Ϋ―²–Η-–¥–Β –Γ–Η―²–Β―Ä –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α, –Α ―¹–Α –≤ ―¹–Η–Μ–Α –Ζ–Α –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Η –Ω–Μ–Ψ―¹–Κ–Η –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Α. –£―ä―Ä―Ö―É ―²–Ψ–≤–Α –≤–Β―΅–Β –Ψ–Κ–Ψ–Μ–Ψ 3 –≥–Ψ–¥–Η–Ϋ–Η ―Ä–Α–±–Ψ―²―è―² –≤ ―¹―ä―²―Ä―É–¥–Ϋ–Η―΅–Β―¹―²–≤–Ψ ―É–Ϋ–Η–≤–Β―Ä―¹–Η―²–Β―²―ä―² –≤ –ï–¥–Η–Ϋ–±―É―Ä–≥, –Ξ–Α―Ä–≤–Α―Ä–¥, –‰–Ϋ–¥–Η–Ι―¹–Κ–Η―è―² –Η–Ϋ―¹―²–Η―²―É―² –Ζ–Α –Ϋ–Α―É―΅–Ϋ–Ψ –Ψ–±―Ä–Α–Ζ–Ψ–≤–Α–Ϋ–Η–Β –Η –Ω―Ä–Ψ―É―΅–≤–Α–Ϋ–Η―è, –€–Α―¹–Α―΅―É–Ζ–Β―²―¹–Κ–Η―è―² ―²–Β―Ö–Ϋ–Ψ–Μ–Ψ–≥–Η―΅–Β–Ϋ –Η–Ϋ―¹―²–Η―²―É―², ―É–Ϋ–Η–≤–Β―Ä―¹–Η―²–Β―²―ä―² –ö–Η–Ψ―²–Ψ –Η –Δ–Θ –£–Η–Β–Ϋ–Α. –Γ–Β–≥–Α –™―Ä―É–Φ–Η–Μ–Β―Ä –Ζ–Α–Β–¥–Ϋ–Ψ ―¹ –Κ–Ψ–Μ–Β–≥–Η –Ψ―² –‰–Ϋ–¥–Η―è –Η –·–Ω–Ψ–Ϋ–Η―è –Ω―É–±–Μ–Η–Κ―É–≤–Α ―¹―²–Α―²–Η―è –≤ ―¹–Ω–Η―¹–Α–Ϋ–Η–Β βÄûPhysical Review LettersβÄ€, –Κ–Ψ―è―²–Ψ –Ω–Ψ―²–≤―ä―Ä–Ε–¥–Α–≤–Α –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β―²–Ψ –Ζ–Α ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β –≤ –Ω–Μ–Ψ―¹–Κ–Α –£―¹–Β–Μ–Β–Ϋ–Α.
–î–≤–Α –Ω―ä―²–Η –Η–Ζ―΅–Η―¹–Μ–Β–Ϋ–Η―è βÄ™ –Β–¥–Η–Ϋ –Η ―¹―ä―â ―Ä–Β–Ζ―É–Μ―²–Α―²
βÄû–ê–Κ–Ψ –Κ–≤–Α–Ϋ―²–Ψ–≤–Α―²–Α –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è –≤ –Ω–Μ–Ψ―¹–Κ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ –¥–Ψ–Ω―É―¹–Κ–Α ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Ψ –Ψ–Ω–Η―¹–Α–Ϋ–Η–Β ―΅―Ä–Β–Ζ –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Α –Κ–≤–Α–Ϋ―²–Ψ–≤–Α ―²–Β–Ψ―Ä–Η―è, ―²–Ψ–≥–Α–≤–Α –±–Η ―¹–Μ–Β–¥–≤–Α–Μ–Ψ –¥–Α –Β –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Ψ –Η–Ζ―΅–Η―¹–Μ―è–≤–Α–Ϋ–Β―²–Ψ –Ϋ–Α ―³–Η–Ζ–Η―΅–Ϋ–Η –≤–Β–Μ–Η―΅–Η–Ϋ–Η –Ϋ–Α –±–Α–Ζ–Α―²–Α –Ϋ–Α –¥–≤–Β―²–Β ―²–Β–Ψ―Ä–Η–Η –Η ―Ä–Β–Ζ―É–Μ―²–Α―²–Η―²–Β –±–Η ―²―Ä―è–±–≤–Α–Μ–Ψ –¥–Α ―¹―ä–≤–Ω–Α–¥–Α―²βÄ€, –Κ–Α–Ζ–≤–Α –™―Ä―É–Φ–Η–Μ–Β―Ä. –ù–Α–Ι-–≤–Β―΅–Β –Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –Β–¥–Ϋ–Ψ –Κ–Μ―é―΅–Ψ–≤–Ψ ―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Ϋ–Α –Κ–≤–Α–Ϋ―²–Ψ–≤–Α―²–Α –Φ–Β―Ö–Α–Ϋ–Η–Κ–Α βÄ™ –Κ–≤–Α–Ϋ―²–Ψ–≤–Ψ―²–Ψ –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η–Β βÄ™ –¥–Α –±―ä–¥–Β –Ψ―²–Κ―Ä–Η―²–Ψ –Η –Ψ―² ―¹―²―Ä–Α–Ϋ–Α –Ϋ–Α ―²–Β–Ψ―Ä–Η―è―²–Α –Ζ–Α –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è―²–Α.
–ê–Κ–Ψ –Κ–≤–Α–Ϋ―²–Ψ–≤–Η―²–Β ―΅–Α―¹―²–Η―Ü–Η –Η–Φ–Α―² –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η–Β, –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η ―²–Β –Ϋ–Β –Ω–Ψ–¥–Μ–Β–Ε–Α―² –Ϋ–Α ―Ä–Α–Ζ–¥–Β–Μ–Ϋ–Ψ –Ψ–Ω–Η―¹–Α–Ϋ–Η–Β βÄ™ –Ψ―² –≥–Μ–Β–¥–Ϋ–Α ―²–Ψ―΅–Κ–Α –Ϋ–Α –Κ–≤–Α–Ϋ―²–Ψ–≤–Α―²–Α ―³–Η–Ζ–Η–Κ–Α ―²–Β –Ψ–±―Ä–Α–Ζ―É–≤–Α―² –Β–¥–Η–Ϋ ―Ü―è–Μ –Ψ–±–Β–Κ―², –¥–Ψ―Ä–Η –¥–Α ―¹–Β –Ϋ–Α–Φ–Η―Ä–Α―² –Ϋ–Α –≥–Ψ–Μ–Β–Φ–Η ―Ä–Α–Ζ―¹―²–Ψ―è–Ϋ–Η―è –Β–¥–Ϋ–Α –Ψ―² –¥―Ä―É–≥–Α. –€―è―Ä–Κ–Α –Ζ–Α –Κ–≤–Α–Ϋ―²–Ψ–≤–Ψ-–Φ–Β―Ö–Α–Ϋ–Η―΅–Ϋ–Ψ―²–Ψ –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η–Β –Β ―².–Ϋ–Α―Ä. βÄû–Β–Ϋ―²―Ä–Ψ–Ω–Η―è –Ϋ–Α –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η–Β―²–ΨβÄ€. –½–Α–Β–¥–Ϋ–Ψ ―¹ –ê―Ä―é–Ϋ –ë–Α–≥―Ö–Η, –†―É–¥―Ä–Α–Ϋ–Η–Μ –ë–Α―¹―É –Η –€–Α–Κ―¹ –†–Η–Ι–≥–Β–Μ –î–Α–Ϋ–Η–Β–Μ –™―Ä―É–Φ–Η–Μ–Β―Ä ―É―¹–Ω―è–≤–Α –¥–Α –Ω–Ψ–Κ–Α–Ε–Β, ―΅–Β –Ζ–Α ―²–Α–Ζ–Η –Β–Ϋ―²―Ä–Ψ–Ω–Η―è –Ϋ–Α –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η–Β―²–Ψ –≤ –Β–¥–Ϋ–Α ―²–Β–Ψ―Ä–Η―è –Ζ–Α –Κ–≤–Α–Ϋ―²–Ψ–≤–Α―²–Α –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è –≤ –Ω–Μ–Ψ―¹–Κ–Α –£―¹–Β–Μ–Β–Ϋ–Α –Η –Β–¥–Ϋ–Α –Κ–≤–Α–Ϋ―²–Ψ–≤–Α ―²–Β–Ψ―Ä–Η―è –Ϋ–Α –Ω–Ψ–Μ–Β―²–Ψ ―¹ –Ω–Ψ-–Φ–Α–Μ―ä–Κ –±―Ä–Ψ–Ι –Η–Ζ–Φ–Β―Ä–Β–Ϋ–Η―è ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―²–Η―²–Β –¥–Β–Ι―¹―²–≤–Η―²–Β–Μ–Ϋ–Ψ ―¹–Α –Β–¥–Ϋ–Η –Η ―¹―ä―â–Η.
βÄû–Δ–Ψ–≤–Α –Η–Ζ―΅–Η―¹–Μ–Β–Ϋ–Η–Β –Ω–Ψ―²–≤―ä―Ä–Ε–¥–Α–≤–Α –Ϋ–Α―à–Β―²–Ψ –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β, ―΅–Β ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η―è―² –Ω―Ä–Η–Ϋ―Ü–Η–Ω –Φ–Ψ–Ε–Β –¥–Α –±―ä–¥–Β ―Ä–Β–Α–Μ–Η–Ζ–Η―Ä–Α–Ϋ –Η –≤ –Ω–Μ–Ψ―¹–Κ–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ-–≤―Ä–Β–Φ–Β. –Γ―ä―â–Β–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Ψ ―²–Ψ–≤–Α –Β –Η –Ζ–Ϋ–Α–Κ –Ζ–Α –≤–Α–Μ–Η–¥–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α ―²–Ψ–Ζ–Η –Ω―Ä–Η–Ϋ―Ü–Η–Ω –≤ –Ϋ–Α―à–Α―²–Α –£―¹–Β–Μ–Β–Ϋ–ΑβÄ€, –Ψ–±―è―¹–Ϋ―è–≤–Α –€–Α–Κ―¹ –†–Η–Ι–≥–Β–Μ, ―¹―²–Η–Ω–Β–Ϋ–¥–Η–Α–Ϋ―² –Ω–Ψ –Ω―Ä–Ψ–≥―Ä–Α–Φ–Α―²–Α –Ζ–Α –Ϋ–Α―É―΅–Ϋ–Ψ ―Ä–Α–Ζ–≤–Η―²–Η–Β –Ϋ–Α –ê–≤―¹―²―Ä–Η–Ι―¹–Κ–Α―²–Α –Α–Κ–Α–¥–Β–Φ–Η―è –Ϋ–Α –Ϋ–Α―É–Κ–Η―²–Β –≤ –Η–Ζ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ―¹–Κ–Α―²–Α –≥―Ä―É–Ω–Α –Ϋ–Α –î–Α–Ϋ–Η–Β–Μ –™―Ä―É–Φ–Η–Μ–Β―Ä. βÄû–Γ–Α–Φ –Ω–Ψ ―¹–Β–±–Β ―¹–Η ―³–Α–Κ―²―ä―², ―΅–Β –≥–Ψ–≤–Ψ―Ä–Β–Ι–Κ–Η –Ζ–Α –≥―Ä–Α–≤–Η―²–Α―Ü–Η―è –Φ–Ψ–Ε–Β–Φ –¥–Α –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Φ–Β –Κ–≤–Α–Ϋ―²–Ψ–≤–Ψ-–Η–Ϋ―³–Ψ―Ä–Φ–Α―Ü–Η–Ψ–Ϋ–Ϋ–Η –Ω–Ψ–Ϋ―è―²–Η―è –Κ–Α―²–Ψ –Β–Ϋ―²―Ä–Ψ–Ω–Η―è –Ϋ–Α –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η–Β―²–Ψ, –Β ―¹–Φ―É―â–Α–≤–Α―â –Η –¥–Ψ –Ω―Ä–Β–¥–Η –Ϋ―è–Κ–Ψ–Μ–Κ–Ψ –≥–Ψ–¥–Η–Ϋ–Η –±–Β―à–Β ―²―Ä―É–¥–Ϋ–Ψ –¥–Α ―¹–Η –Ω―Ä–Β–¥―¹―²–Α–≤–Η–Φ –Ω–Ψ–¥–Ψ–±–Ϋ–Ψ –Ϋ–Β―â–Ψ. –Δ–Ψ–≤–Α, ―΅–Β ―¹–Β–≥–Α –¥–Ψ―Ä–Η –Φ–Ψ–Ε–Β–Φ –¥–Α –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Φ–Β ―²–Ψ–Ζ–Η ―³–Α–Κ―² –Κ–Α―²–Ψ –Η–Ϋ―¹―²―Ä―É–Φ–Β–Ϋ―² –Ζ–Α ―²–Β―¹―²–≤–Α–Ϋ–Β –≤–Α–Μ–Η–¥–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α ―Ö–Ψ–Μ–Ψ–≥―Ä–Α―³―¹–Κ–Η―è –Ω―Ä–Η–Ϋ―Ü–Η–Ω βÄ™ –Ψ―â–Β –Ω–Ψ–≤–Β―΅–Β, ―΅–Β ―²–Ψ–Ζ–Η ―²–Β―¹―² –±–Β―à–Β ―¹–Ω–Ψ–Μ―É―΅–Μ–Η–≤ βÄ™ –Β –Ϋ–Α–Η―¹―²–Η–Ϋ–Α –Ζ–Α–±–Β–Μ–Β–Ε–Η―²–Β–Μ–Ϋ–ΨβÄ€, –Κ–Α–Ζ–≤–Α –î–Α–Ϋ–Η–Β–Μ –™―Ä―É–Φ–Η–Μ–Β―Ä.
–Γ ―²–Ψ–≤–Α –¥–Α–Μ–Β―΅ –Ϋ–Β –Β –¥–Ψ–Κ–Α–Ζ–Α–Ϋ–Ψ, ―΅–Β –Ε–Η–≤–Β–Β–Φ –≤ ―Ö–Ψ–Μ–Ψ–≥―Ä–Α–Φ–Α. –½–Ϋ–Α―Ü–Η―²–Β –≤ –Ω–Ψ–Μ–Ζ–Α –Ϋ–Α –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η―è―²–Α –Ψ–±–Α―΅–Β –Ζ–Α –≤–Α–Μ–Η–¥–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α –Ω―Ä–Η–Ϋ―Ü–Η–Ω–Α –Ϋ–Α ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β―²–Ψ¬†–≤ –Ϋ–Α―à–Α―²–Α ―Ä–Β–Α–Μ–Ϋ–Α –£―¹–Β–Μ–Β–Ϋ–Α –Η–Ζ–≥–Μ–Β–Ε–¥–Α –≤―¹–Β –Ω–Ψ–≤–Β―΅–Β ―¹–Β ―É–≤–Β–Μ–Η―΅–Α–≤–Α―².




















–ö–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
–€–Ψ–Μ―è, ―Ä–Β–≥–Η―¹―²―Ä–Η―Ä–Α–Ι―²–Β ―¹–Β –Ψ―² T–Θ–ö!
–ê–Κ–Ψ –≤–Β―΅–Β –Η–Φ–Α―²–Β ―Ä–Β–≥–Η―¹―²―Ä–Α―Ü–Η―è, –Ϋ–Α―²–Η―¹–Ϋ–Β―²–Β –Δ–Θ–ö!
14033
1
16.01 2018 –≤ 15:28
–ü–Ψ―¹–Μ–Β–¥–Ϋ–Η –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
4I4ATA
–ù–Ψ–≤, ―¹–Κ―Ä–Η―² –¥–Ψ―¹–Β–≥–Α –≤―Ö–Ψ–¥ –≤ –Ω–Η―Ä–Α–Φ–Η–¥–Α―²–Α –Ϋ–Α –€–Η–Κ–Β―Ä–Η–Ϋ –Β –Ψ―²–Κ―Ä–Η―² –Ω–Ψ –Α–Ϋ–Ψ–Φ–Α–Μ–Η–Η –Ω―Ä–Η ―¹–Κ–Α–Ϋ–Η―Ä–Α–Ϋ–Β
YKoshev
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
Johnny B Goode
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
Gunteer
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
–Ξ―Ä–Η―¹―²–Η―è–Ϋ–Η–Ϋ
–Δ–Ψ–≤–Α –Β –Κ―Ä–Α–Μ―è―² –Ϋ–Α ―²–Η–Κ–≤–Η―²–Β: –Δ–Η–Κ–≤–Α―²–Α –Φ―É ―²–Β–Ε–Η –Ϋ–Α–¥ –Β–¥–Η–Ϋ –Β–¥–Η–Ϋ ―²–Ψ–Ϋ