

–ē–ī–ł–Ĺ –ĺ—ā –Ĺ–į–Ļ-–ł–∑–≤–Ķ—Ā—ā–Ĺ–ł—ā–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł –Ĺ–į –Ĺ–į—ą–Ķ—ā–ĺ –≤—Ä–Ķ–ľ–Ķ, –Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ –Ĺ–į –Ĺ–į–≥—Ä–į–ī–į—ā–į "–ź–Ī–Ķ–Ľ" –ł –ľ–Ķ–ī–į–Ľ–į "–§–ł–Ľ–ī—Ā" –ú–į–Ļ–ļ—ä–Ľ –ź—ā–ł—Ź¬†(Michael Atiyah) –ł–∑–Ľ–ĺ–∂–ł –Ĺ–į —Ā–≤–ĺ–Ī–ĺ–ī–Ķ–Ĺ –ī–ĺ—Ā—ā—ä–Ņ¬†—Ā–≤–ĺ–Ķ—ā–ĺ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ĺ–į —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –†–ł–ľ–į–Ĺ - –ľ–ĺ–∂–Ķ –Ī–ł –Ĺ–į–Ļ-–ł–∑–≤–Ķ—Ā—ā–Ĺ–į—ā–į –Ĺ–Ķ—Ä–Ķ—ą–Ķ–Ĺ–į –∑–į–ī–į—á–į –≤ –ĺ–Ī–Ľ–į—Ā—ā—ā–į –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į.
–Ē—Ä—É–≥–ł—ā–Ķ —Ā–Ņ–Ķ—Ü–ł–į–Ľ–ł—Ā—ā–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł –≤—Ā–Ķ –ĺ—Č–Ķ –Ĺ–Ķ —Ā–į –Ņ–ĺ—ā–≤—ä—Ä–ī–ł–Ľ–ł –ī–į–Ľ–ł —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ķ –≤—Ź—Ä–Ĺ–į, –∑–į—ā–ĺ–≤–į –Ķ —ā–≤—ä—Ä–ī–Ķ —Ä–į–Ĺ–ĺ –ī–į —Ā–Ķ –≥–ĺ–≤–ĺ—Ä–ł –∑–į –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ĺ–į –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł—Ź –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ.
–Ę–Ķ–ļ—Ā—ā—ä—ā –Ķ –ī–ĺ—Ā—ā—ä–Ņ–Ķ–Ĺ —ā—É–ļ.
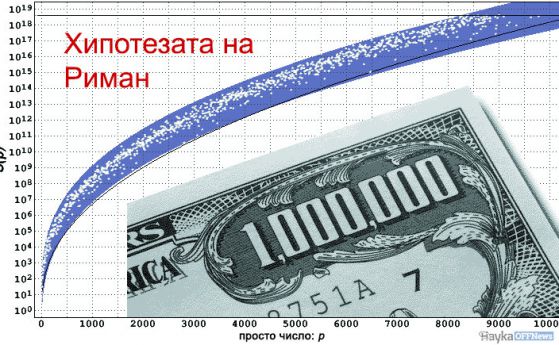
–ė–∑–≤–Ķ—Ā—ā–Ĺ–ł—Ź—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –ĺ—ā 19-—ā–ł –≤–Ķ–ļ –Ď–Ķ—Ä–Ĺ—Ö–į—Ä–ī –†–ł–ľ–į–Ĺ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į —Ā–ł –Ņ—Ä–Ķ–∑ 1859 –≥–ĺ–ī–ł–Ĺ–į. –Ę—Ź –≥–Ľ–į—Ā–ł:
"–í—Ā–ł—á–ļ–ł –Ĺ–Ķ—ā—Ä–ł–≤–ł–į–Ľ–Ĺ–ł –Ĺ—É–Ľ–ł –Ĺ–į –†–ł–ľ–į–Ĺ–ĺ–≤–į—ā–į –ī–∑–Ķ—ā–į-—Ą—É–Ĺ–ļ—Ü–ł—Ź (—Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł—ā–Ķ –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł—Ź –į—Ä–≥—É–ľ–Ķ–Ĺ—ā, –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–Ķ–≤—Ä—ä—Č–į —Ą—É–Ĺ–ļ—Ü–ł—Ź—ā–į –≤ –Ĺ—É–Ľ–į) –Ľ–Ķ–∂–į—ā –Ĺ–į –Ľ–ł–Ĺ–ł—Ź—ā–į ¬Ĺ + it, —ā.–Ķ. —ā—Ź—Ö–Ĺ–į—ā–į —Ä–Ķ–į–Ľ–Ĺ–į —á–į—Ā—ā –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į ¬Ĺ".
–ź–ļ–ĺ –≤–ł –∑–≤—É—á–ł –Ĺ–Ķ—Ä–į–∑–Ī–ł—Ä–į–Ķ–ľ–ĺ, –∑–į–Ņ–ĺ–∑–Ĺ–į–Ļ—ā–Ķ —Ā–Ķ —Ā –ĺ–Ņ–ł—ā–į –Ĺ–į –ĺ–Ī—Ź—Ā–Ĺ–Ķ–Ĺ–ł–Ķ¬†‚Äě–•–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –†–ł–ľ–į–Ĺ –∑–į –Ľ–į–ł—Ü–ł‚ÄĚ.
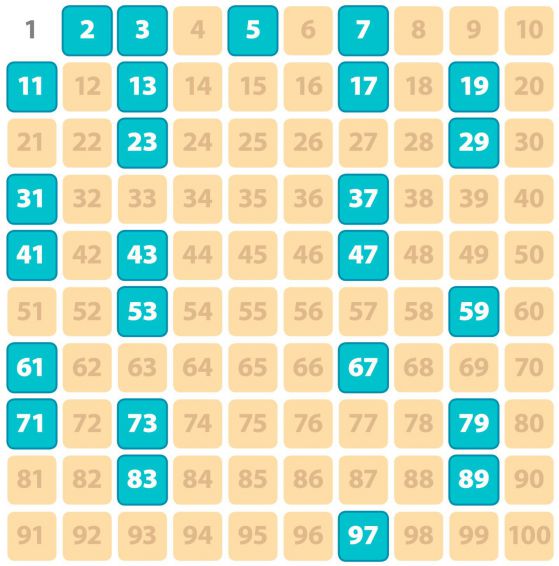
–†–į–∑–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–ł—ā–Ķ —á–ł—Ā–Ľ–į –ľ–Ķ–∂–ī—É –≤—Ā–ł—á–ļ–ł –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ł —á–ł—Ā–Ľ–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ĺ–Ķ —Ā–Ľ–Ķ–ī–≤–į –Ĺ—Ź–ļ–į–ļ–≤–į –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā. –Ě–Ķ–ľ—Ā–ļ–ł—Ź—ā –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –Ď–Ķ—Ä–Ĺ—Ö–į—Ä–ī –†–ł–ľ–į–Ĺ –∑–į–Ī–Ķ–Ľ—Ź–∑–≤–į –Ņ—Ä–Ķ–∑ 1859, —á–Ķ —á–Ķ—Ā—ā–ĺ—ā–į—ā–į –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–ł—ā–Ķ —á–ł—Ā–Ľ–į –Ķ –ľ–Ĺ–ĺ–≥–ĺ —ā—Ź—Ā–Ĺ–ĺ —Ā–≤—ä—Ä–∑–į–Ĺ–į —Ā –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ķ–ī–Ĺ–į —Ā–Ľ–ĺ–∂–Ĺ–į —Ą—É–Ĺ–ļ—Ü–ł—Ź, –ļ–ĺ—Ź—ā–ĺ –Ķ –ĺ—ā–ļ—Ä–ł–Ľ –õ–Ķ–ĺ–Ĺ–į—Ä–ī –ě–Ļ–Ľ–Ķ—Ä, –Ĺ–ĺ –†–ł–ľ–į–Ĺ –≤–∑–Ķ–Ľ —ā–į–∑–ł –ł–ī–Ķ—Ź –ł —Ź —Ä–į–∑–≤–ł–Ľ –Ņ–ĺ —Ā—ä–≤—Ā–Ķ–ľ –Ĺ–ĺ–≤ –Ĺ–į—á–ł–Ĺ, —á—Ä–Ķ–∑ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ĺ–Ķ –Ĺ–į —ā.–Ĺ–į—Ä. –ī–∑–Ķ—ā–į-—Ą—É–Ĺ–ļ—Ü–ł—Ź.
–°–į–ľ–į—ā–į –ī–∑–Ķ—ā–į-—Ą—É–Ĺ–ļ—Ü–ł—Ź –≤—ä–∑–Ĺ–ł–ļ–≤–į –≤ –ľ–Ĺ–ĺ–≥–ĺ —Ä–į–∑–ī–Ķ–Ľ–ł –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į. –í —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į —á–ł—Ā–Ľ–į—ā–į, —ā—Ź –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–į —Ā —Ä–į–∑–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ņ—Ä–ĺ—Ā—ā–ł—ā–Ķ¬†—á–ł—Ā–Ľ–į. –Ę–ĺ–≤–į –Ķ –Ķ–ī–Ĺ–į –ĺ—ā –Ĺ–į–Ļ-–ł–∑–≤–Ķ—Ā—ā–Ĺ–ł—ā–Ķ –ł –Ĺ–į–Ļ-–≤–į–∂–Ĺ–ł—ā–Ķ –∑–į–ī–į—á–ł¬†–≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į. –ú–į—ā–Ķ–ľ–į—ā–ł–ļ—ä—ā –Ē–į–≤–ł–ī –•–ł–Ľ–Ī–Ķ—Ä—ā, –∂–ł–≤—Ź–Ľ –≤ –ļ—Ä–į—Ź –Ĺ–į XIX –≤–Ķ–ļ –ł –Ĺ–į—á–į–Ľ–ĺ—ā–ĺ –Ĺ–į XX, –≤ –ĺ—ā–≥–ĺ–≤–ĺ—Ä –Ĺ–į –≤—ä–Ņ—Ä–ĺ—Ā–į, –ļ–į–ļ–≤–ĺ –Ī–ł –Ņ–ĺ–Ņ–ł—ā–į–Ľ –į–ļ–ĺ —Ā–Ķ —Ā—ä–Ī—É–ī–ł —Ā–Ľ–Ķ–ī —Ö–ł–Ľ—Ź–ī–į –≥–ĺ–ī–ł–Ĺ–ł, –∑–į—Ź–≤–ł, —á–Ķ —Č–Ķ —Ā–Ķ –∑–į–ł–Ĺ—ā–Ķ—Ä–Ķ—Ā—É–≤–į¬†–ī–ĺ–ļ–į–∑–į–Ĺ–į –Ľ–ł –Ķ —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –†–ł–ľ–į–Ĺ.
–Ē–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ, –ļ–ĺ–Ķ—ā–ĺ –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į –ź—ā–ł—Ź, –Ķ –ľ–Ĺ–ĺ–≥–ĺ –ļ—Ä–į—ā–ļ–ĺ - –∑–į–Ķ–ī–Ĺ–ĺ —Ā –≤—ä–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –ł —Ā–Ņ–ł—Ā—ä–ļ–į –Ĺ–į –Ľ–ł—ā–Ķ—Ä–į—ā—É—Ä–į—ā–į¬†–Ķ —Ā–į–ľ–ĺ –Ņ–Ķ—ā —Ā—ā—Ä–į–Ĺ–ł—Ü–ł. –°–į–ľ–ł—Ź—ā –į–≤—ā–ĺ—Ä –Ĺ–į—Ä–ł—á–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ —É–ī–ł–≤–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–ĺ –ł –ĺ–Ī—Ź—Ā–Ĺ—Ź–≤–į, —á–Ķ –Ķ –ĺ—Ā–Ĺ–ĺ–≤–į–≤–į–Ĺ–ĺ –Ĺ–į —Ä–į–Ī–ĺ—ā–į—ā–į –Ĺ–į —Ą–ĺ–Ĺ –Ě–ĺ–Ļ–ľ–į–Ĺ (1936 –≥.),¬†–§—Ä–ł–ī—Ä–ł—Ö –•–ł—Ä–∂–Ķ–Ī—Ä—É—á (1954 –≥.) –ł –Ē–ł—Ä–į–ļ (1928).
–ß—Ä–Ķ–∑ –ļ–ĺ–ľ–Ī–ł–Ĺ–ł—Ä–į–Ĺ–Ķ –Ĺ–į —ā–Ķ—Ö–Ĺ–ł—ā–Ķ –Ņ—Ä–ĺ–∑—Ä–Ķ–Ĺ–ł—Ź –ł –Ņ—Ä–ł–Ķ–ľ–į–Ĺ–Ķ—ā–ĺ, —á–Ķ —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –†–ł–ľ–į–Ĺ –Ķ –Ĺ–Ķ–≤—Ź—Ä–Ĺ–į, –ź—ā–ł—Ź —ā–≤—ä—Ä–ī–ł, —á–Ķ –ī–ĺ—Ā—ā–ł–≥–į –ī–ĺ –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł–Ķ, –ļ–ĺ–Ķ—ā–ĺ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į, —á–Ķ —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į —ā—Ä—Ź–Ī–≤–į –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –ī–į –Ķ –≤—Ź—Ä–Ĺ–į. "–ė–∑–≥–Ľ–Ķ–∂–ī–į –ļ–į—ā–ĺ —á—É–ī–ĺ", –ļ–ĺ–ľ–Ķ–Ĺ—ā–ł—Ä–į –ź—ā–ł—Ź –∑–į NewScientist, "–Ĺ–ĺ —ā–≤—ä—Ä–ī—Ź, —á–Ķ —Ü—Ź–Ľ–į—ā–į —Ä–į–Ī–ĺ—ā–į –Ī–Ķ –ł–∑–≤—ä—Ä—ą–Ķ–Ĺ–į –Ņ—Ä–Ķ–ī–ł 70 –≥–ĺ–ī–ł–Ĺ–ł".
"–†–Ķ—ą–Ķ—ā–Ķ —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –†–ł–ľ–į–Ĺ –ł —Č–Ķ —Ā—ā–į–Ĺ–Ķ—ā–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł. –ź–ļ–ĺ –≤–Ķ—á–Ķ —Ā—ā–Ķ –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł, —Č–Ķ —Ā—ā–į–Ĺ–Ķ—ā–Ķ —Ā–ļ–į–Ĺ–ī–į–Ľ–Ĺ–ł", –∑–į—Ź–≤–ł –ź—ā–ł—Ź –Ņ–ĺ –≤—Ä–Ķ–ľ–Ķ –Ĺ–į –ł–Ĺ—ā–Ķ—Ä–≤—é—ā–ĺ. "–Ě–ł–ļ–ĺ–Ļ –Ĺ–Ķ –≤—Ź—Ä–≤–į –≤ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ĺ–į —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –†–ł–ľ–į–Ĺ, –∑–į—Č–ĺ—ā–ĺ –Ķ –ľ–Ĺ–ĺ–≥–ĺ —ā—Ä—É–ī–Ĺ–ĺ. –Ě–ł–ļ–ĺ–Ļ –Ĺ–Ķ —Ź –Ķ –ī–ĺ–ļ–į–∑–į–Ľ –ī–ĺ—Ā–Ķ–≥–į, —ā–į–ļ–į —á–Ķ –∑–į—Č–ĺ –Ĺ—Ź–ļ–ĺ–Ļ —ā—Ä—Ź–Ī–≤–į –ī–į —Ź –ī–ĺ–ļ–į–∂–Ķ —Ā–Ķ–≥–į? –ě—Ā–≤–Ķ–Ĺ –į–ļ–ĺ, —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ, –ł–ľ–į —Ā—ä–≤—Ā–Ķ–ľ –Ĺ–ĺ–≤–į –ł–ī–Ķ—Ź".
–ü–ĺ—Ä–į–ī–ł –ļ—Ä–į—ā–ļ–ĺ—Ā—ā—ā–į –Ĺ–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ —Ā–Ķ –ĺ—á–į–ļ–≤–į —Ä–Ķ–į–ļ—Ü–ł—Ź—ā–į –Ĺ–į –Ņ—Ä–ĺ—Ą–Ķ—Ā–ł–ĺ–Ĺ–į–Ľ–Ĺ–į—ā–į –ĺ–Ī—Č–Ĺ–ĺ—Ā—ā –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –ī–į –Ī—ä–ī–Ķ –ī–ĺ—Ā—ā–į –Ī—ä—Ä–∑–į.
–ó–į —Ä–į–∑–Ľ–ł–ļ–į –ĺ—ā –Ľ–į–ļ–ĺ–Ĺ–ł—á–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į —ā–ĺ–≤–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ, –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –∑–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į –Ĺ–į –§–Ķ—Ä–ľ–į –ł —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –ü–ĺ–į–Ĺ–ļ–į—Ä–Ķ –∑–į–Ķ–ľ–į—Ö–į —Ā—ā–ĺ—ā–ł—Ü–ł —Ā—ā—Ä–į–Ĺ–ł—Ü–ł, –į –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į abc-—Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į¬†–®–ł–Ĺ–ł—á–ł –ú–ĺ—á–ł–∑—É–ļ–ł –Ķ –Ĺ–į –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā 500 —Ā—ā—Ä–į–Ĺ–ł—Ü–ł¬†–ł¬†—Ā–Ņ–Ķ—Ü–ł–į–Ľ–ł—Ā—ā–ł—ā–Ķ –ĺ—Č–Ķ –Ĺ–Ķ —Ā–į —É—Ā–Ņ–Ķ–Ľ–ł –ī–į –≥–ĺ –Ņ—Ä–ĺ–≤–Ķ—Ä—Ź—ā –ł –ī–į —Ā—ā–ł–≥–Ĺ–į—ā¬†–ī–ĺ –ļ–ĺ–Ĺ—Ā–Ķ–Ĺ—Ā—É—Ā, –≤—ä–Ņ—Ä–Ķ–ļ–ł —ą–Ķ—Ā—ā—ā–Ķ –≥–ĺ–ī–ł–Ĺ–ł, –ł–∑–ľ–ł–Ĺ–į–Ľ–ł –ĺ—ā –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–Ķ—ā–ĺ –ľ—É.
–†–ĺ–ī–Ķ–Ĺ–ł—Ź—ā –Ņ—Ä–Ķ–∑ 1929 –≥. –ú–į–Ļ–ļ—ä–Ľ –ź—ā–ł—Ź (Michael Atiyah) –Ķ –Ķ–ī–Ĺ–į –ĺ—ā –Ĺ–į–Ļ-–ł–∑–≤–Ķ—Ā—ā–Ĺ–ł—ā–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł —Ą–ł–≥—É—Ä–ł –≤—ä–≤ –í–Ķ–Ľ–ł–ļ–ĺ–Ī—Ä–ł—ā–į–Ĺ–ł—Ź - —ā–ĺ–Ļ –Ķ –Ņ–ĺ–Ľ—É—á–ł–Ľ –ī–≤–Ķ –Ĺ–į–≥—Ä–į–ī–ł, —á–Ķ—Ā—ā–ĺ –Ĺ–į—Ä–ł—á–į–Ĺ–ł –Ě–ĺ–Ī–Ķ–Ľ–ĺ–≤–ł—ā–Ķ –Ĺ–į–≥—Ä–į–ī–ł –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į - –ľ–Ķ–ī–į–Ľ–į –§–ł–Ľ–ī—Ā –ł –Ĺ–į–≥—Ä–į–ī–į—ā–į –ź–Ī–Ķ–Ľ. –Ę–ĺ–Ļ —Ā—ä—Č–ĺ —ā–į–ļ–į, –Ņ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–ĺ –≤—Ä–Ķ–ľ–Ķ, –Ķ –Ī–ł–Ľ –Ņ—Ä–Ķ–∑–ł–ī–Ķ–Ĺ—ā –Ĺ–į –õ–ĺ–Ĺ–ī–ĺ–Ĺ—Ā–ļ–ĺ—ā–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ –ī—Ä—É–∂–Ķ—Ā—ā–≤–ĺ, –ö—Ä–į–Ľ—Ā–ļ–ĺ—ā–ĺ –ī—Ä—É–∂–Ķ—Ā—ā–≤–ĺ –ł –ö—Ä–į–Ľ—Ā–ļ–ĺ—ā–ĺ –ī—Ä—É–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –ē–ī–ł–Ĺ–Ī—É—Ä–≥.
–ź–ļ–ĺ —Ā–Ķ –Ņ–ĺ—ā–≤—ä—Ä–ī–ł —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –†–ł–ľ–į–Ĺ, —ā–ĺ–≤–į —Č–Ķ –Ī—ä–ī–Ķ –Ĺ–į–ł—Ā—ā–ł–Ĺ–į –≥–ĺ–Ľ—Ź–ľ–į –Ĺ–ĺ–≤–ł–Ĺ–į.




















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
YKoshev
–Ē–ĺ–ļ–ĺ–Ľ–ļ–ĺ —Ā—ä–≤–ľ–Ķ—Ā—ā–ł–ľ–ł —Ā–į –ľ–ł–Ĺ–Ķ—Ä–į–Ľ–Ĺ–ĺ-—Ā—É—Ä–ĺ–≤–ł–Ĺ–Ĺ–ł—Ź—ā –ĺ—ā—Ä–į—Ā—ä–Ľ –ł —á–ł—Ā—ā–į—ā–į –ĺ–ļ–ĺ–Ľ–Ĺ–į —Ā—Ä–Ķ–ī–į?
–ö–ĺ–∑–ĺ–Ĺ
–ú–ł—Ā—ā–Ķ—Ä–ł–ĺ–∑–Ķ–Ĺ —á–Ķ—Ä–Ķ–Ņ –Ĺ–į –≥—Ä—ä—Ü–ļ–ł —Ö–ĺ–ľ–ł–Ĺ–ł–Ĺ –Ķ –ī–į—ā–ł—Ä–į–Ĺ –Ĺ–į –Ņ–ĺ–Ĺ–Ķ 286 000 –≥–ĺ–ī–ł–Ĺ–ł
Peter Petrov
–°–Ľ–Ķ–ī –ľ–Ĺ–ĺ–≥–ĺ–ļ—Ä–į—ā–Ĺ–ł –Ķ–ļ—Ā–Ņ–Ľ–ĺ–∑–ł–ł –Ĺ–ĺ–≤ —ā–Ķ—Ā—ā –∑–į –ľ–Ķ–≥–į—Ä–į–ļ–Ķ—ā–į—ā–į –Ĺ–į –ú—ä—Ā–ļ
–Ņ–ĺ–Ņ –Ē—Ä—ä–≤—á–ĺ
–ď–Ľ–Ķ–ī–į–Ļ—ā–Ķ –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā –Ĺ–į –∂–ł–≤–ĺ –ļ–į–ļ –Ĺ–ĺ–≤–ĺ–ĺ—ā–ļ—Ä–ł—ā–ł—Ź—ā "–ľ–Ķ–∂–ī—É–∑–≤–Ķ–∑–ī–Ķ–Ĺ –Ņ–ĺ—Ā–Ķ—ā–ł—ā–Ķ–Ľ" 3I/ATLAS —Ā–Ķ —É—Ā—ā—Ä–Ķ–ľ—Ź–≤–į –ļ—ä–ľ –Ĺ–į—Ā