

–Ę–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ĺ–ĺ, –Ņ—ä—Ä–≤–ł—Ź—ā –į–Ľ–≥–Ķ–Ī—Ä–ł—á–Ķ–Ĺ —Ą—Ä–į–ļ—ā–į–Ľ - –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –Ķ –ĺ–Ņ–ł—Ā–į–Ĺ –∑–į –Ņ—ä—Ä–≤–ł –Ņ—ä—ā –Ņ—Ä–Ķ–∑ 1918 –ĺ—ā —Ą—Ä–Ķ–Ĺ—Ā–ļ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –ď–į—Ā—ā–ĺ–Ĺ –Ė—é–Ľ–ł–į , –ļ–ĺ–Ļ—ā–ĺ –Ņ–ĺ —ā–ĺ–≤–į –≤—Ä–Ķ–ľ–Ķ –Ī–ł–Ľ –≤–ĺ–Ķ–Ĺ–Ĺ–į –Ī–ĺ–Ľ–Ĺ–ł—Ü–į –ł —Ā–Ķ –≤—ä–∑—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į–Ľ –ĺ—ā –Ĺ–į—Ä–į–Ĺ—Ź–≤–į–Ĺ–ł—Ź—ā–į —Ā–ł –ĺ—ā –ü—ä—Ä–≤–į—ā–į —Ā–≤–Ķ—ā–ĺ–≤–Ĺ–į –≤–ĺ–Ļ–Ĺ–į.
–ü–ĺ —Ā—ä—Č–ĺ—ā–ĺ –≤—Ä–Ķ–ľ–Ķ —Ä–į–Ī–ĺ—ā–ł –ł –ü–ł–Ķ—Ä –§–į—ā—É, —Ā—ä—Č–ĺ –Ņ–ĺ –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į z ‚Üí z2+c –ł –ī–≤–į–ľ–į—ā–į –Ņ–ĺ–Ľ—É—á–į–≤–į—ā –Ņ–ĺ —Ā—ä—Č–Ķ—Ā—ā–≤–ĺ –Ķ–ī–Ĺ–ł –ł —Ā—ä—Č–ł —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł, –Ĺ–ĺ —Ā–ļ–ĺ—Ä–ĺ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–ł—Ź—ā–į –ł–ľ —Ā–į –∑–į–Ī—Ä–į–≤–Ķ–Ĺ–ł, –ī–ĺ–ļ–į—ā–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ—ä—ā –ĺ—ā IBM, –Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ĺ–Ķ –ł–ľ –≤–ī—ä—Ö–≤–į –Ĺ–ĺ–≤ –∂–ł–≤–ĺ—ā, –Ī–Ľ–į–≥–ĺ–ī–į—Ä–Ķ–Ĺ–ł–Ķ –Ĺ–į —Ä–į–∑–≤–ł–≤–į—Č–į—ā–į —Ā–Ķ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–į —ā–Ķ—Ö–Ĺ–ł–ļ–į. –ė–Ĺ—ā–Ķ–Ľ–Ķ–ļ—ā—É–į–Ľ–Ĺ–ł—Ź—ā –Ņ–ĺ–ī–≤–ł–≥ –Ĺ–į –Ē–∂—É–Ľ–ł—Ź –ł –§–į—ā—É –Ķ –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ –∑–į–Ī–Ķ–Ľ–Ķ–∂–ł—ā–Ķ–Ľ–Ķ–Ĺ, –∑–į—Č–ĺ—ā–ĺ —Ā–į —Ä–į–∑—á–ł—ā–į–Ľ–ł —Ā–į–ľ–ĺ –Ĺ–į —Ā–≤–ĺ—Ź—ā–į —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā –∑–į –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ĺ –ľ–ł—Ā–Ľ–Ķ–Ĺ–Ķ, –į –∑–į–ī–į—á–į—ā–į –Ī–Ķ–∑ –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –ļ–ĺ–ľ–Ņ—é—ā—Ä–ł –Ķ —Ā–Ķ—Ä–ł–ĺ–∑–Ĺ–ĺ –Ņ—Ä–Ķ–ī–ł–∑–≤–ł–ļ–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –∑–į —á–ĺ–≤–Ķ—ą–ļ–ł—ā–Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł.
–ź–Ľ–≥–Ķ–Ī—Ä–ł—á–Ĺ–ł—ā–Ķ —Ą—Ä–į–ļ—ā–į–Ľ–ł –≤—ä–∑–Ĺ–ł–ļ–≤–į—ā –≤ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ł –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ł, –∑–į—ā–ĺ–≤–į —Ā–Ķ –Ĺ–į—Ä–ł—á–į—ā –ł –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–ł –ł –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ł. –Ę–Ķ —Ā–į –ĺ–Ī–Ķ–ļ—ā –Ĺ–į –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ –≤–Ĺ–ł–ľ–į–Ĺ–ł–Ķ, –∑–į—Č–ĺ—ā–ĺ –≤—ä–∑–Ņ—Ä–ĺ–ł–∑–≤–Ķ–∂–ī–į—ā –ĺ–≥—Ä–ĺ–ľ–Ĺ–ĺ –Ī–ĺ–≥–į—ā—Ā—ā–≤–ĺ –ĺ—ā –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ł —Ą–ł–≥—É—Ä–ł —Ā–į–ľ–ĺ –ĺ—ā –Ķ–ī–ł–Ĺ —Ā—ä–≤—Ā–Ķ–ľ –Ņ—Ä–ĺ—Ā—ā –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ –ł —Ā–į —ā—Ź—Ā–Ĺ–ĺ —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā—ä—Ā —Ā—ä–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–į—ā–į —ā–Ķ–ĺ—Ä–ł—Ź –Ĺ–į —Ö–į–ĺ—Ā–į.
–Ę—ä–Ļ –ļ–į—ā–ĺ.—Ā–Ķ —Ä–į–∑–≤–ł–≤–į—ā –≤ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—ā–į —Ä–į–≤–Ĺ–ł–Ĺ–į, –Ĺ–Ķ–ļ–į —Ā–ł –Ņ—Ä–ł–Ņ–ĺ–ľ–Ĺ–ł–ľ –ļ–į–ļ–≤–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—Ö–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į.
–ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į
–ó–į –ī–į —Ā–Ķ –Ņ–ĺ—Ā—ā—Ä–ĺ–ł —Ą—Ä–į–ļ—ā–į–Ľ—ä—ā¬†–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –ł–ľ–į–ľ–Ķ –Ĺ—É–∂–ī–į –ĺ—ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł —á–ł—Ā–Ľ–į. –ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į —Ā–Ķ —Ā—ä—Ā—ā–ĺ—Ź—ā –ĺ—ā –ī–≤–Ķ —á–į—Ā—ā–ł - —Ä–Ķ–į–Ľ–Ĺ–į –ł –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į, –į —Ü—Ź–Ľ–ĺ—ā–ĺ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ —Ā–Ķ –ĺ–∑–Ĺ–į—á–į–≤–į —ā–į–ļ–į: z¬†=a+bi , –ļ–į—ā–ĺ i —Ā–Ķ –Ĺ–į—Ä–ł—á–į –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į –Ķ–ī–ł–Ĺ–ł—Ü–į, –∑–į—Č–ĺ—ā–ĺ –į–ļ–ĺ —Ā–Ķ –Ņ–ĺ–≤–ī–ł–≥–Ĺ–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā, –Ņ–ĺ–Ľ—É—á–į–≤–į–ľ–Ķ -1, —ā.¬†–Ķ. i2¬†=¬†‚Äď1; a –ł b —Ā–į —Ä–Ķ–į–Ľ–Ĺ–ł —á–ł—Ā–Ľ–į, ¬†–ļ–į—ā–ĺ a¬†—Ā–Ķ –Ĺ–į—Ä–ł—á–į —Ä–Ķ–į–Ľ–Ĺ–į, –į¬†b¬†—Ā–Ķ –Ĺ–į—Ä–ł—á–į –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į —á–į—Ā—ā –Ĺ–į —á–ł—Ā–Ľ–ĺ—ā–ĺ.
–ź–ļ–ĺ b¬†=¬†0, —ā–ĺ –≤–ľ–Ķ—Ā—ā–ĺ a¬†+¬†0i –Ņ–ł—ą–Ķ–ľ –Ņ—Ä–ĺ—Ā—ā–嬆a - —ā.–Ķ. —Ä–Ķ–į–Ľ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į —Ā–į —á–į—Ā—ā–Ķ–Ĺ —Ā–Ľ—É—á–į–Ļ –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł —á–ł—Ā–Ľ–į.
–°—ä–Ī–ł—Ä–į–Ĺ–Ķ—ā–ĺ –ł –ł–∑–≤–į–∂–ī–į–Ĺ–Ķ—ā–ĺ —Ā—ā–į–≤–į—ā –Ņ–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ (a¬†+¬†bi)¬†¬Ī¬†(c¬†+¬†di)¬†= (a¬†¬Ī¬†c)¬†+¬†(b¬†¬Ī¬†d)i, –į¬†—É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ¬†- –Ņ–嬆–Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ (a¬†+¬†bi)¬†¬∑¬†(c¬†+¬†di)¬†= (ac¬†‚Ästbd)¬†+¬†(ad¬†+¬†bc)i (—ā—É–ļ —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į, —á–Ķ i2¬†=¬†‚Äď1). –Ę–Ķ–∑–ł –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź —Č–Ķ —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ –≤ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į–Ĺ–ł—ā–Ķ –Ņ–ĺ-–ļ—ä—Ā–Ĺ–ĺ —Ą—Ä–į–ļ—ā–į–Ľ–ł.
 |
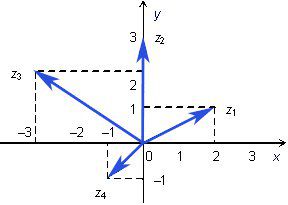 |
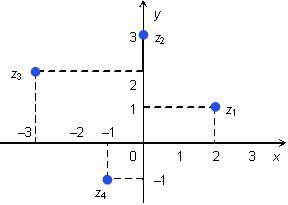
| z1 = 2+i; z2 = 3i; z3 = --3+2i; z4 = -1-i; | |z1| = ‚ąö5; |z2| = 3; |z3| = ‚ąö13; |z4| = ‚ąö2; |
–ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —Ā—ä–Ī–ł—Ä–į—ā, –ł–∑–≤–į–∂–ī–į—ā, —É–ľ–Ĺ–ĺ–∂–į–≤–į—ā, –ī–Ķ–Ľ—Ź—ā –ł –≤—Ā–ł—á–ļ–ł –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł –į–Ľ–≥–Ķ–Ī—Ä–ł—á–Ĺ–ł –ī–Ķ–Ļ—Ā—ā–≤–ł—Ź, –Ĺ–ĺ –Ĺ–Ķ –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ —Ā—Ä–į–≤–Ĺ—Ź–≤–į—ā. –ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł –ļ–į—ā–ĺ —ā–ĺ—á–ļ–į –≤ –Ē–Ķ–ļ–į—Ä—ā–ĺ–≤–į—ā–į —Ä–į–≤–Ĺ–ł–Ĺ–į, –≤ –ļ–ĺ—Ź—ā–ĺ x –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į –Ķ —Ä–Ķ–į–Ľ–Ĺ–į—ā–į —á–į—Ā—ā, –į y –Ķ –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā—ä—ā –Ĺ–į –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į—ā–į —á–į—Ā—ā b.
–ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į –ł–ľ–į—ā —É–ī–ĺ–Ī–Ĺ–ĺ –ł –Ĺ–į–≥–Ľ–Ķ–ī–Ĺ–ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź–Ĺ–Ķ - —á–ł—Ā–Ľ–ĺ—ā–ĺ z¬†=¬†a¬†+¬†bi –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ł–∑–ĺ–Ī—Ä–į–∑–Ķ–Ĺ–ĺ –ł –ļ–į—ā–ĺ –≤–Ķ–ļ—ā–ĺ—Ä —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł –Ĺ–į –≤—ä—Ä—Ö–į (a,¬†b) . –°—É–ľ–į—ā–į –ĺ—ā –ī–≤–Ķ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł —á–ł—Ā–Ľ–į —Ā–Ķ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź –ļ–į—ā–ĺ —Ā—É–ľ–į—ā–į –Ĺ–į —Ā—ä–ĺ—ā–≤–Ķ—ā–Ĺ–ł—ā–Ķ –≤–Ķ–ļ—ā–ĺ—Ä–ł –Ņ–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ –Ĺ–į —É—Ā–Ņ–ĺ—Ä–Ķ–ī–Ĺ–ł–ļ–į. –ü–ĺ —ā–Ķ–ĺ—Ä–Ķ–ľ–į—ā–į –Ĺ–į –ü–ł—ā–į–≥–ĺ—Ä –ī—ä–Ľ–∂–ł–Ĺ–į –Ĺ–į –≤–Ķ–ļ—ā–ĺ—Ä–į —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł (a,¬†b) –Ķ —Ä–į–≤–Ĺ–į –Ĺ–į¬†![]()
–Ę–į–∑–ł –≤–Ķ–Ľ–ł—á–ł–Ĺ–į —Ā–Ķ –Ĺ–į—Ä–ł—á–į –ľ–ĺ–ī—É–Ľ –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ—ā–ĺ —á–ł—Ā–Ľ–ĺ z¬†=¬†a¬†+¬†bi –ł —Ā–Ķ –ĺ–∑–Ĺ–į—á–į–≤–į —Ā |z|. –™–≥—ä–Ľ—ä—ā, –ļ–ĺ–Ļ—ā–ĺ —ā–ĺ–∑–ł –≤–Ķ–ļ—ā–ĺ—Ä —Ā–ļ–Ľ—é—á–≤–į —Ā –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ–Ĺ–į—ā–į –Ņ–ĺ—Ā–ĺ–ļ–į –Ĺ–į –ĺ—Ā —Ö (–ĺ—ā—á–Ķ—ā–Ķ–Ĺ –ĺ–Ī—Ä–į—ā–Ĺ–ĺ –Ĺ–į —á–į—Ā–ĺ–≤–Ĺ–ł–ļ–ĺ–≤–į—ā–į —Ā—ā—Ä–Ķ–Ľ–ļ–į) —Ā–Ķ –Ĺ–į—Ä–ł—á–į –į—Ä–≥—É–ľ–Ķ–Ĺ—ā –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ—ā–ĺ —á–ł—Ā–Ľ–ĺ z . –ź—Ä–≥—É–ľ–Ķ–Ĺ—ā—ä—ā –Ĺ–Ķ –Ķ –Ķ–ī–Ĺ–ĺ–∑–Ĺ–į—á–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ, –į —ā–ĺ—á–Ĺ–ĺ —Ā–į–ľ–ĺ –ī–ĺ –ī–ĺ–Ī–į–≤—Ź–Ĺ–Ķ—ā–ĺ –Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, –ļ—Ä–į—ā–Ĺ–į –Ĺ–į 2ŌÄ —Ä–į–ī–ł–į–Ĺ–į (–ł–Ľ–ł 360¬į)¬†- —Ź—Ā–Ĺ–ĺ –Ķ, —á–Ķ –Ņ—ä–Ľ–Ķ–Ĺ –ĺ–Ī–ĺ—Ä–ĺ—ā –ĺ–ļ–ĺ–Ľ–ĺ –Ĺ–į—á–į–Ľ–ĺ—ā–ĺ –Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł—ā–Ķ –Ĺ—Ź–ľ–į –ī–į –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł –≤–Ķ–ļ—ā–ĺ—Ä–į.
–ě—Ā–Ĺ–ĺ–≤–Ĺ–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ–ł
–ė–ľ–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł –≤–ł–ī–ĺ–≤–Ķ –Ĺ–Ķ–Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ł —Ą—Ä–į–ļ—ā–į–Ľ–ł, –Ĺ–ĺ –≤ –Ĺ–į–Ļ-–ĺ–Ī—Č–ł—Ź —Ā–Ľ—É—á–į–Ļ –į–Ľ–≥–Ķ–Ī—Ä–ł—á–Ĺ–ł—Ź —Ą—Ä–į–ļ—ā–į–Ľ —Ā–Ķ –∑–į–ī–į–≤–į —Ā –ł—ā–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ
–Ě–Ķ–ļ–į f(z) –Ķ –Ņ–ĺ–Ľ–ł–Ĺ–ĺ–ľ , –į z0 –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ. –Ē–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ —Ā–Ľ–Ķ–ī–Ĺ–į—ā–į –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā:
z0, z1=f(z0), z2=f(f(z0))=f(z1), z3=f(f(f(z0)))=f(f(z1))= f(z2), ...
–í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā –Ĺ–į—á–į–Ľ–Ĺ–į—ā–į —ā–ĺ—á–ļ–ł z0 , –Ņ—Ä–ł –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ –Ĺ–į –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į —ā–į–∑–ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā, –ļ–ĺ–≥–į—ā–ĺ n –ļ–Ľ–ĺ–Ĺ–ł –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā, —ā–į–∑–ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ī—ä—Ä–∂–ł –Ņ–ĺ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ –Ĺ–į—á–ł–Ĺ:
- –ī–į –ļ–Ľ–ĺ–Ĺ–Ĺ–ł –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā¬†
- –ī–į –ļ–Ľ–ĺ–Ĺ–Ĺ–ł –ļ—ä–ľ¬†–ļ—Ä–į–Ļ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ,¬†
- –ī–į –Ņ—Ä–ĺ—Ź–≤—Ź–≤–į —Ü–ł–ļ–Ľ–ł—á–Ĺ–ĺ –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –≤ –Ĺ—Ź–ļ–į–ļ–≤–ł –≥—Ä–į–Ĺ–ł—Ü–ł, –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä:¬†z1, z2, z3,z1, z2, z3...
- –ī–į —Ā–Ķ –ī—ä—Ä–∂–ł —Ö–į–ĺ—ā–ł—á–Ĺ–ĺ, —ā.–Ķ. –ī–į –Ĺ–Ķ –Ņ–ĺ–ļ–į–∑–≤–į –Ĺ–ł—ā–ĺ –Ķ–ī–ł–Ĺ –ĺ—ā –≥–ĺ—Ä–Ĺ–ł—ā–Ķ —ā—Ä–ł —ā–ł–Ņ–į –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ.
–ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į
| –Ē–į —Ā–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł–ľ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—ā–į —Ä–į–≤–Ĺ–ł–Ĺ–į, —Ü—Ź–Ľ–į—ā–į –ł–∑–Ņ—ä–Ľ–Ĺ–Ķ—ā–į —Ā —ā–ĺ—á–ļ–ł, —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į—Č–ł –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į. –Ē–į –Ĺ–į—á–Ķ—Ä—ā–į–Ķ–ľ –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā –ĺ–ļ–ĺ–Ľ–ĺ –Ĺ–į—á–į–Ľ–ĺ—ā–ĺ –Ĺ–į –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–Ĺ–į—ā–į —Ā–ł—Ā—ā–Ķ–ľ–į—Ā —Ä–į–ī–ł—É—Ā 1. –Ě—Ź–ļ–ĺ–ł —ā–ĺ—á–ļ–ł —Č–Ķ –Ņ–ĺ–Ņ–į–ī–Ĺ–į—ā –≤—ä—ā—Ä–Ķ –≤ –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į (—á–Ķ—Ä–≤–Ķ–Ĺ–ł—ā–Ķ), –į –ī—Ä—É–≥–ł (–∑–Ķ–Ľ–Ķ–Ĺ–ł—ā–Ķ) - –≤—ä—ā—Ä–Ķ. –Ē–į –≥–ł –Ņ–ĺ–≤–ī–ł–≥–Ĺ–Ķ–ľ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā. | 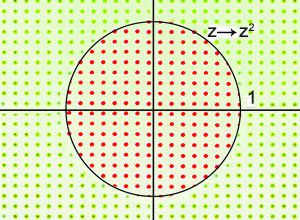 |
| –†–Ķ–∑—É–Ľ—ā–į—ā—ä—ā –ĺ—ā –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ł—ā–Ķ –ł—ā–Ķ—Ä–į—Ü–ł–ł –Ĺ–į –Ņ–ĺ–≤–ī–ł–≥–į–Ĺ–Ķ –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ –Ķ, —á–Ķ —á–Ķ—Ä–≤–Ķ–Ĺ–ł—ā–Ķ —ā–ĺ—á–ļ–ł –ĺ—Ā—ā–į–≤–į—ā –≤—ä—ā—Ä–Ķ –≤ –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į, –į –∑–Ķ–Ľ–Ķ–Ĺ–ł—ā–Ķ —Ā–Ķ —Ä–į–∑–Ī—Ź–≥–≤–į—ā –ī–į–Ľ–Ķ—á–Ķ –ĺ—ā –Ĺ–Ķ—Ź. –Ę–į–∑–ł –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā –Ķ –∑–į–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ –ĺ—ā –ł—ā–Ķ—Ä–į—Ü–ł–ł, –ł–∑–≤—ä—Ä—ą–≤–į—Č–ł –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–ł—Ź –Ņ–ĺ–≤–ī–ł–≥–į–Ĺ–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā. –Ę–ĺ—á–Ĺ–ł—ā–Ķ –ł–∑–≤—ä–Ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į, —Ā–Ľ–Ķ–ī –Ĺ–Ķ–ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–ł –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑—É–≤–į–Ĺ–ł—Ź –Ņ–ĺ–≤–ī–ł–≥–į–Ĺ–Ķ –Ĺ–į –ļ–≤–į–ī—Ä–į—ā –ĺ—ā–ł–≤–į—ā –≤ –Ī–Ķ–∑–ļ—Ä–į—Ź. | 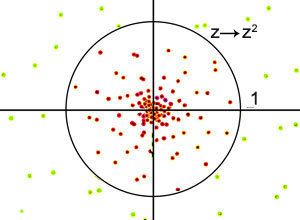 |
–ź–ļ–ĺ –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ—ä—ā —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–ł –Ĺ–į z ‚Üí z2+c, –ļ—ä–ī–Ķ—ā–ĺ c –Ķ –Ĺ—Ź–ļ–į–ļ–≤–ĺ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ, –∑–į –≤—Ā—Ź–ļ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–ĺ c , –ĺ—á–Ķ—Ä—ā–į–Ĺ–ł—Ź—ā–į –Ĺ–į —Ą–ĺ—Ä–ľ–į—ā–į –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –∑–į–Ņ–ĺ—á–≤–į –ī–į —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź. –ö–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ–ĺ –Ņ–ĺ –ľ–ĺ–ī—É–Ľ c , —ā–ĺ–Ľ–ļ–ĺ–≤–į —ā–ĺ —Ā–ł–Ľ–Ĺ–ĺ —Ā–Ķ –ĺ—ā–ļ–Ľ–ĺ–Ĺ—Ź–≤–į –ĺ—ā —Ą–ĺ—Ä–ľ–į—ā–į –Ĺ–į –ļ—Ä—ä–≥. –Ē–ĺ–Ī–į–≤—Ź–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ņ–į—Ä–į–ľ–Ķ—ā—ä—Ä–į c –ļ—ä–ľ —ā–ĺ—á–ļ–ł—ā–Ķ –ĺ—ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—ā–į —Ä–į–≤–Ĺ–ł–Ĺ–į "—Č–Ķ –∑–į–Ņ—Ä–į—ā–ł" –Ĺ—Ź–ļ–ĺ–ł –ĺ—ā —ā—Ź—Ö –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā—ā–į, –į –ī—Ä—É–≥–ł —Č–Ķ –Ĺ–į—Ā–ĺ—á–ł –ļ—ä–ľ —Ü–Ķ–Ĺ—ā—ä—Ä–į. –Ę–į–ļ–į —Č–Ķ —Ā–Ķ –ĺ–Ī—Ä–į–∑—É–≤–į—ā –Ĺ–ĺ–≤–ł —Ä–į–∑–Ĺ–ĺ–ĺ–Ī—Ä–į–∑–ł —Ą–ĺ—Ä–ľ–ł:
 |
 |
 |
 |
 |
 |
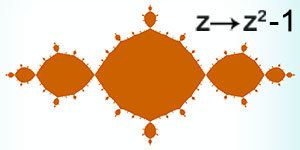 |
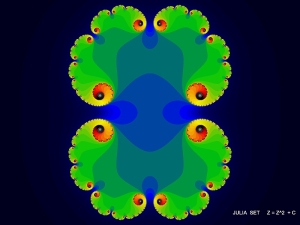
–°–ł–ľ–Ķ—ā—Ä–ł—Ź—ā–į –≤ –ĺ—á–Ķ—Ä—ā–į–Ĺ–ł—Ź—ā–į –Ĺ–į –∑–į–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł—Ź –≥–ĺ–≤–ĺ—Ä–ł –∑–į –Ľ–ł–Ņ—Ā–į –Ĺ–į –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–į —á–į—Ā—ā, –į –∑–į–≤–ł—Ö—Ä—Ź–Ĺ–ł—Ź—ā–į - –∑–į –Ĺ–į–Ľ–ł—á–ł–Ķ—ā–ĺ –Ļ. | |
–ü–ĺ–Ľ–ł–Ĺ–ĺ–ľ—ä—ā f(z) –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į –ļ–į—ā–嬆–∑–į–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į, –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ —ā–ĺ—á–ļ–ł, –ļ–ĺ–ł—ā–ĺ –Ĺ–Ķ —Ā–Ķ —Ā—ā—Ä–Ķ–ľ—Ź—ā –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā. –ź –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –§–į—ā—É –Ķ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –ł –į–ļ–ĺ –Ņ–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ĺ—ā–ĺ –Ķ –∑–į—ā–≤–ĺ—Ä–Ķ–Ĺ–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ, —ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –§–į—ā—É –Ķ –ĺ—ā–≤–ĺ—Ä–Ķ–Ĺ–ĺ.
–Ę–ĺ—á–ļ–ł—ā–Ķ, –Ľ–Ķ–∂–į—Č–ł –Ĺ–į –≥—Ä–į–Ĺ–ł—Ü–į—ā–į –ľ–Ķ–∂–ī—É –ī–≤–Ķ—ā–Ķ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į –ł–ľ–į—ā —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ—ā–ĺ –Ņ—Ä–ł –ľ–Ĺ–ĺ–≥–ĺ –ľ–į–Ľ–ļ–į –Ņ—Ä–ĺ–ľ—Ź–Ĺ–į –Ĺ–į –Ņ–ĺ–∑–ł—Ü–ł—Ź—ā–į, —Ö–į—Ä–į–ļ—ā–Ķ—Ä—ä—ā –Ĺ–į –Ņ–ĺ–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –ł–ľ –ī—Ä–į—Ā—ā–ł—á–Ĺ–ĺ –ī–į —Ā–Ķ –ł–∑–ľ–Ķ–Ĺ—Ź. –ď—Ä–į–Ĺ–ł—Ü–į—ā–į –Ĺ–į –∑–į–Ņ—ä–Ľ–Ĺ–Ķ–Ĺ–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –ł–ľ–į —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ł —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł —Ā—ä—Ā —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–ł —á–į—Ā—ā–ł, —ā—Ź –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į.
–ď—Ä–į—Ą–ł—á–Ĺ–ł—ā–Ķ –ł–Ĺ—ā–Ķ—Ä–Ņ—Ä–Ķ—ā–į—Ü–ł–ł

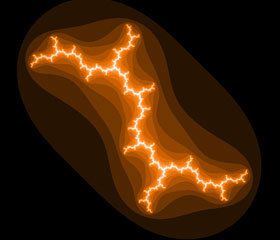
–Ę–ĺ–≤–į –ļ—Ä–į—Ā–ł–≤–ĺ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ –Ķ —ā–ĺ—á–Ĺ–ĺ —Ā–į–ľ–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į, –ļ–ĺ–Ķ—ā–ĺ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā —Ā–į–ľ–ĺ –ĺ—ā —ā–ĺ—á–ļ–ł –ł –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ł–∑—Ä–ł—Ā—É–≤–į–Ĺ–ĺ —ā–į–ļ–į. –Ě–į –ļ–į—Ä—ā–ł–Ĺ–ļ–į—ā–į —Ā–Ķ –≤–ł–∂–ī–į—ā —ā–ĺ—á–ļ–ł—ā–Ķ –ĺ—ā –ĺ–ļ–ĺ–Ľ–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –ł –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ķ –Ņ–ĺ-—Ź—Ä–ļ–į —ā–ĺ—á–ļ–į—ā–į, —ā–ĺ–Ľ–ļ–ĺ–≤–į –Ķ –Ņ–ĺ-–Ī–Ľ–ł–∑–ļ–ĺ –ī–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –ł —ā–ĺ–Ľ–ļ–ĺ–≤–į –Ņ–ĺ–≤–Ķ—á–Ķ –ł—ā–Ķ—Ä–į—Ü–ł–ł —Ā–į –Ļ –Ĺ–Ķ–ĺ–Ī—Ö–ĺ–ī–ł–ľ–ł –∑–į –ī–į —Ā–Ķ –ĺ—ā–ī–į–Ľ–Ķ—á–ł.
 |
|
||||||||||
| –ü—Ä–ł c = i –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į —Ā–Ķ –Ņ—Ä–Ķ–≤—Ä–į—Č–į –≤ –ī–Ķ–Ĺ–ī—Ä–ł—ā - –ī—ä—Ä–≤–ĺ–≤–ł–ī–Ĺ–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į, —Ā—Ä–Ķ—Č–į—Č–į —Ā–Ķ –≤ –ľ–ł–Ĺ–Ķ—Ä–į–Ľ–ĺ–≥–ł—Ź—ā–į, –ł –≤—ä–≤ —Ą–ł–∑–ł–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į, –į —ā—É–ļ –Ĺ–į–Ņ–ĺ–ľ–Ĺ—Ź –Ĺ–į —Ā–≤–Ķ—ā–ļ–į–≤–ł—Ü–į (—ā–Ķ —Ā—ä—Č–ĺ –ł–ľ–į—ā —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–į —Ā—ā—Ä—É–ļ—ā—É—Ä–į | –ö–į–ļ —Č–Ķ –ł–∑–≥–Ľ–Ķ–∂–ī–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į, –į–ļ–ĺ —Ā–Ķ —Ā–ľ–Ķ–Ĺ–ł —Ā—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –ĺ—ā —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į z ‚Üí z2+c –≤–ľ–Ķ—Ā—ā–ĺ 2, —Ā 3, 4, 5, 6. |
||||||||||
–í—Ä—ä–∑–ļ–į—ā–į –ľ–Ķ–∂–ī—É –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į—ā–į –Ĺ–į –Ė—é–Ľ–ł–į –ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā
–ú–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –Ė—é–Ľ–ł–į –ł –§–į—ā—É –ĺ—ā–ļ—Ä–ł–Ľ–ł, —á–Ķ –∑–į –≤—Ā–Ķ–ļ–ł –Ņ–į—Ä–į–ľ–Ķ—ā—ä—Ä c —Ā–Ķ –Ņ–ĺ–Ľ—É—á–į–≤–į—ā –ī–≤–į –≤–ł–ī–į —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź:
- –ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–į —Ą–ł–≥—É—Ä–į –ł–Ľ–ł
- —ā.–Ĺ. –Ņ—Ä–į—Ö –Ĺ–į –§–į—ā—É (—Ö–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ķ–Ĺ –Ĺ–į –Ņ—Ä–į—Ö–į –Ĺ–į –ö–į–Ĺ—ā–ĺ—Ä), –ļ–ĺ–Ļ—ā–ĺ —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā –Ī–Ķ–∑–ļ—Ä–į–Ķ–Ĺ –Ī—Ä–ĺ–Ļ –Ĺ–Ķ—Ā–≤—ä—Ä–∑–į–Ĺ–ł –Ķ–ī–Ĺ–į —Ā –ī—Ä—É–≥–į —ā–ĺ—á–ļ–ł, —Ä–į–∑—Ö–≤—ä—Ä–Ľ–Ķ–Ĺ–ł –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ –Ĺ–į –Ņ—Ä–į—ą–ł–Ĺ–ļ–ł –ł –ł–ľ–į —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā –Ĺ—É–Ľ–į.
–ü–ĺ–Ĺ—Ź—ā–ł—Ź—ā–į "–Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–ĺ" –ł "—Ö–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ĺ–ĺ" —Ā–į –ĺ—ā –ĺ–Ī–Ľ–į—Ā—ā—ā–į –Ĺ–į —ā–ĺ–Ņ–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į –ł —Ā —ā—Ź—Ö –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –∑–į–Ņ–ĺ–∑–Ĺ–į–Ķ—ā–Ķ –≤ —ā–Ķ–ľ–į—ā–į "–•–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į –Ĺ–į –ü–ĺ–į–Ĺ–ļ–į—Ä–Ķ".
–ź–ļ–ĺ –Ĺ–į–Ĺ–Ķ—Ā–Ķ–ľ –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –ĺ—ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—ā–į —Ä–į–≤–Ĺ–ł–Ĺ–į —Ā—ä—Ā —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā –Ņ–į—Ä–į–ľ–Ķ—ā—ä—Ä–į c, –∑–į –ļ–ĺ–Ļ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –Ķ –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–ĺ –ł –Ņ—Ä–Ķ—Ā–ļ–ĺ—á–ł–ľ —ā–ĺ—á–ļ–ł—ā–Ķ —Ā—ä—Ā —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł –Ĺ–į c, –ļ–ĺ–ł—ā–ĺ –ī–į–≤–į—ā –Ĺ–Ķ—Ā–≤—ä—Ä–∑–į–Ĺ–ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į, —Ä–Ķ–∑—É–Ľ—ā–į—ā—ä—ā —Č–Ķ –Ī—ä–ī–Ķ —Ą—Ä–į–ļ—ā–į–Ľ—ä—ā –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā. –Ě–į –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į (–ł–Ľ–ł –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į) –ĺ—ā –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į –Ĺ—Ź–ļ–į–ļ—ä–≤ —Ą—Ä–į–ļ—ā–į–Ľ –Ė—é–Ľ–ł–į.
–ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā
–ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, –ļ–ĺ–Ķ—ā–ĺ –Ī–ł–Ľ–ĺ –Ņ–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–ĺ –ĺ—ā –Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, –Ĺ–į–≤—Ź—Ä–Ĺ–ĺ –Ķ –Ņ—ä—Ä–≤–į—ā–į –į—Ā–ĺ—Ü–ł–į—Ü–ł—Ź, –≤—ä–∑–Ĺ–ł–ļ–≤–į—Č–į —É —Ö–ĺ—Ä–į—ā–į, –ļ–ĺ–≥–į—ā–ĺ —á—É—Ź—ā "—Ą—Ä–į–ļ—ā–į–Ľ".
–Ę–ĺ–∑–ł —Ą—Ä–į–ļ—ā–į–Ľ —Ā–Ķ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į –Ņ–ĺ —Ā—ä—Č–į—ā–į –Ņ—Ä–ĺ—Ā—ā –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ–į –ļ–į—ā–ĺ —Ą—Ä–į–ļ—ā–į–Ľ–į –Ĺ–į –Ė—é–Ľ–ł–į
z ‚Üí z2+c,
–Ě–ĺ —ā—É–ļ –į–ļ—Ü–Ķ–Ĺ—ā—ä—ā –Ķ –ī—Ä—É–≥–į–ī–Ķ, –∑–į—Č–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł —Ā–į–ľ–ĺ –ĺ—ā —ā–ĺ—á–ļ–ł, –∑–į –ļ–ĺ–ł—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į –ľ–ĺ–∂–Ķ –Ī—ä–ī–Ķ –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–ĺ.
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ĺ–Ķ –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā. –ö—Ä–ł—ā–Ķ—Ä–ł–Ļ –∑–į –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–ĺ—Ā—ā –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į
–ź–ļ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–ľ –ļ—Ä–ł—ā–Ķ—Ä–ł—Ź –∑–į –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–ĺ—Ā—ā –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į, —Č–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –ł–∑–ĺ–Ī—Ä–į–∑–ł–ľ –ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā. –° –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā–ĺ–∑–ł –ļ—Ä–ł—ā–Ķ—Ä–ł–Ļ —Ā–į —Ā–Ķ —Ā–Ņ—Ä–į–≤–ł–Ľ–ł –ł –Ė—é–Ľ–ł–į –ł –§–į—ā—É. –Ę–Ķ —Ā–į –ĺ—ā–ļ—Ä–ł–Ľ–ł, —á–Ķ —ā–ĺ–∑–ł —ā–ĺ–∑–ł –Ĺ–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī —ā—Ä—É–ī–Ķ–Ĺ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ —Ä–Ķ—ą–Ķ–Ĺ —Ā –Ņ—Ä–ĺ—Ā—ā–ł —Ā–ľ–Ķ—ā–ļ–ł.
–Ē–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā—ā–į –ĺ—ā —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł –Ĺ–į zn, –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ł –ĺ—ā —Ą–ĺ—Ä–ľ—É–Ľ–į—ā–į
–ź–ļ–ĺ —ā—Ź –Ĺ–Ķ –ļ–Ľ–ĺ–Ĺ–ł –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā, —ā–ĺ –į—Ā–ĺ—Ü–ł–ł—Ä–į–Ĺ–ĺ—ā–ĺ —Ā—ä—Ā —Ā—ä—Č–į—ā–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā –Ĺ–į –Ņ–į—Ä–į–ľ–Ķ—ā—ä—Ä–į c –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ė—é–Ľ–ł–į —Č–Ķ –Ī—ä–ī–Ķ –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–ĺ –ł —ā–ĺ—á–ļ–į—ā–į c —Č–Ķ –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–ł –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā.
–Ě–į –≤—Ā—Ź–ļ–į —ā–ĺ—á–ļ–į –ĺ—ā –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į —Ą—Ä–į–ļ—ā–į–Ľ –Ĺ–į –Ė—é–Ľ–ł–į.
 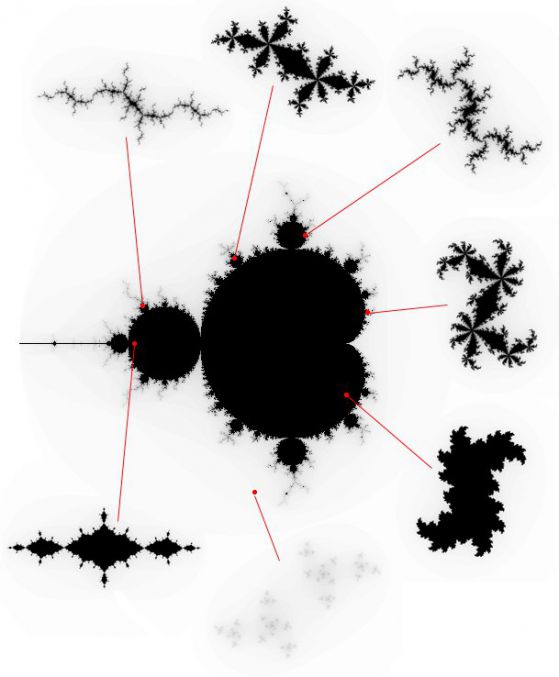
–ö–į–ļ —Ā–Ķ –ł–∑—á–Ķ—Ä—ā–į–≤–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā
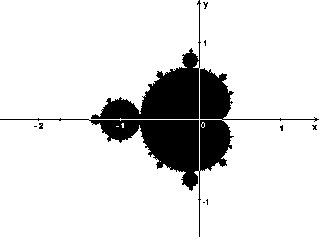 –ó–į –ī–į –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ —ā–ĺ–∑–ł –∑–Ĺ–į–ľ–Ķ–Ĺ–ł—ā —Ą—Ä–į–ļ—ā–į–Ľ –ł—ā–Ķ—Ä–į—Ü–ł–ł—ā–Ķ —Ā–Ķ –ł–∑–Ņ—ä–Ľ–Ĺ—Ź–≤–į—ā –∑–į –≤—Ā—Ź–ļ–į —Ā—ā–į—Ä—ā–ĺ–≤–į —ā–ĺ—á–ļ–į C –≤ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–į –ł–Ľ–ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–į –ĺ–Ī–Ľ–į—Ā—ā - –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—ā–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā. –ė—ā–Ķ—Ä–į—Ü–ł–ĺ–Ĺ–ł—Ź—ā –Ņ—Ä–ĺ—Ü–Ķ—Ā –Ņ—Ä–ĺ–ī—ä–Ľ–∂–į–≤–į –ī–ĺ—ā–ĺ–≥–į–≤–į, –ī–ĺ–ļ–į—ā–ĺ Z[i] –Ĺ–Ķ –ł–∑–Ľ–Ķ–∑–Ķ –ł–∑–≤—ä–Ĺ –≥—Ä–į–Ĺ–ł—Ü–ł—ā–Ķ –Ĺ–į –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā —Ā —Ä–į–ī–ł—É—Ā 2, —Ü–Ķ–Ĺ—ā—ä—Ä—ä—ā –Ĺ–į –ļ–ĺ—Ź—ā–ĺ –Ľ–Ķ–∂–ł –≤ —ā–ĺ—á–ļ–į—ā–į (0,0), (—ā–ĺ–≤–į –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –į—ā—Ä–į–ļ—ā–ĺ—Ä—ä—ā –Ĺ–į –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–į—ā–į —Ā–ł—Ā—ā–Ķ–ľ–į —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į –≤ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā—ā–į), –ł–Ľ–ł —Ā–Ľ–Ķ–ī –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –≥–ĺ–Ľ—Ź–ľ –Ī—Ä–ĺ–Ļ –ł—ā–Ķ—Ä–į—Ü–ł–ł (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä 200-500) Z[i] –∑–į–Ņ–ĺ—á–Ĺ–Ķ –ī–į –ļ–Ľ–ĺ–Ĺ–ł –ļ—ä–ľ –Ĺ—Ź–ļ–į–ļ–≤–į —ā–ĺ—á–ļ–į –ĺ—ā –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į. –í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ—ā–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –≤ —ā–Ķ—á–Ķ–Ĺ–łe –Ĺ–į –ļ–ĺ–ł—ā–ĺ Z[i] –ĺ—Ā—ā–į–≤–į –≤—ä—ā—Ä–Ķ –≤ –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į, –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł —Ü–≤–Ķ—ā–į –Ĺ–į —ā–ĺ—á–ļ–į C (–į–ļ–ĺ Z[i] –ĺ—Ā—ā–į–≤–į –≤—ä—ā—Ä–Ķ –≤ –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į –≤ —ā–Ķ—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –ł—ā–Ķ—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ł—Ź –Ņ—Ä–ĺ—Ü–Ķ—Ā —Ā–Ķ –Ņ—Ä–Ķ–ļ—Ä–į—ā—Ź–≤–į –ł —ā–į–∑–ł —ā–ĺ—á–ļ–į —Ā–Ķ –ĺ—Ü–≤–Ķ—ā—Ź–≤–į –≤ —á–Ķ—Ä–Ĺ–ĺ). –ö—ä–ľ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—ā —ā–ĺ—á–ļ–ł, –ļ–ĺ–ł—ā–ĺ –≤ —ā–Ķ—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ī–Ķ–∑–ļ—Ä–į–Ķ–Ĺ –Ī—Ä–ĺ–Ļ –ł—ā–Ķ—Ä–į—Ü–ł–ł –Ĺ–Ķ –ļ–Ľ–ĺ–Ĺ—Ź—ā –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā (—á–Ķ—Ä–Ĺ–ł —ā–ĺ—á–ļ–ł).
–ó–į –ī–į –Ņ–ĺ—Ā—ā—Ä–ĺ–ł–ľ —ā–ĺ–∑–ł –∑–Ĺ–į–ľ–Ķ–Ĺ–ł—ā —Ą—Ä–į–ļ—ā–į–Ľ –ł—ā–Ķ—Ä–į—Ü–ł–ł—ā–Ķ —Ā–Ķ –ł–∑–Ņ—ä–Ľ–Ĺ—Ź–≤–į—ā –∑–į –≤—Ā—Ź–ļ–į —Ā—ā–į—Ä—ā–ĺ–≤–į —ā–ĺ—á–ļ–į C –≤ –Ņ—Ä–į–≤–ĺ—ä–≥—ä–Ľ–Ĺ–į –ł–Ľ–ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–į –ĺ–Ī–Ľ–į—Ā—ā - –Ņ–ĺ–ī–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—ā–į –Ņ–Ľ–ĺ—Ā–ļ–ĺ—Ā—ā. –ė—ā–Ķ—Ä–į—Ü–ł–ĺ–Ĺ–ł—Ź—ā –Ņ—Ä–ĺ—Ü–Ķ—Ā –Ņ—Ä–ĺ–ī—ä–Ľ–∂–į–≤–į –ī–ĺ—ā–ĺ–≥–į–≤–į, –ī–ĺ–ļ–į—ā–ĺ Z[i] –Ĺ–Ķ –ł–∑–Ľ–Ķ–∑–Ķ –ł–∑–≤—ä–Ĺ –≥—Ä–į–Ĺ–ł—Ü–ł—ā–Ķ –Ĺ–į –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā —Ā —Ä–į–ī–ł—É—Ā 2, —Ü–Ķ–Ĺ—ā—ä—Ä—ä—ā –Ĺ–į –ļ–ĺ—Ź—ā–ĺ –Ľ–Ķ–∂–ł –≤ —ā–ĺ—á–ļ–į—ā–į (0,0), (—ā–ĺ–≤–į –ĺ–∑–Ĺ–į—á–į–≤–į, —á–Ķ –į—ā—Ä–į–ļ—ā–ĺ—Ä—ä—ā –Ĺ–į –ī–ł–Ĺ–į–ľ–ł—á–Ĺ–į—ā–į —Ā–ł—Ā—ā–Ķ–ľ–į —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į –≤ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā—ā–į), –ł–Ľ–ł —Ā–Ľ–Ķ–ī –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –≥–ĺ–Ľ—Ź–ľ –Ī—Ä–ĺ–Ļ –ł—ā–Ķ—Ä–į—Ü–ł–ł (–Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä 200-500) Z[i] –∑–į–Ņ–ĺ—á–Ĺ–Ķ –ī–į –ļ–Ľ–ĺ–Ĺ–ł –ļ—ä–ľ –Ĺ—Ź–ļ–į–ļ–≤–į —ā–ĺ—á–ļ–į –ĺ—ā –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į. –í –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ—ā–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –≤ —ā–Ķ—á–Ķ–Ĺ–łe –Ĺ–į –ļ–ĺ–ł—ā–ĺ Z[i] –ĺ—Ā—ā–į–≤–į –≤—ä—ā—Ä–Ķ –≤ –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į, –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł —Ü–≤–Ķ—ā–į –Ĺ–į —ā–ĺ—á–ļ–į C (–į–ļ–ĺ Z[i] –ĺ—Ā—ā–į–≤–į –≤—ä—ā—Ä–Ķ –≤ –ĺ–ļ—Ä—ä–∂–Ĺ–ĺ—Ā—ā—ā–į –≤ —ā–Ķ—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –ī–ĺ—Ā—ā–į—ā—ä—á–Ĺ–ĺ –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –ł—ā–Ķ—Ä–į—Ü–ł–ĺ–Ĺ–Ĺ–ł—Ź –Ņ—Ä–ĺ—Ü–Ķ—Ā —Ā–Ķ –Ņ—Ä–Ķ–ļ—Ä–į—ā—Ź–≤–į –ł —ā–į–∑–ł —ā–ĺ—á–ļ–į —Ā–Ķ –ĺ—Ü–≤–Ķ—ā—Ź–≤–į –≤ —á–Ķ—Ä–Ĺ–ĺ). –ö—ä–ľ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—ā —ā–ĺ—á–ļ–ł, –ļ–ĺ–ł—ā–ĺ –≤ —ā–Ķ—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ī–Ķ–∑–ļ—Ä–į–Ķ–Ĺ –Ī—Ä–ĺ–Ļ –ł—ā–Ķ—Ä–į—Ü–ł–ł –Ĺ–Ķ –ļ–Ľ–ĺ–Ĺ—Ź—ā –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā (—á–Ķ—Ä–Ĺ–ł —ā–ĺ—á–ļ–ł).
–Ę–ĺ—á–ļ–ł—ā–Ķ, –Ņ—Ä–ł–Ĺ–į–ī–Ľ–Ķ–∂–į—Č–ł –Ĺ–į –≥—Ä–į–Ĺ–ł—Ü–į—ā–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ (–ł–ľ–Ķ–Ĺ–Ĺ–ĺ —ā–į–ľ –≤—ä–∑–Ĺ–ł–ļ–≤–į—ā —Ā–Ľ–ĺ–∂–Ĺ–ł —Ā—ā—Ä—É–ļ—ā—É—Ä–ł) –ļ–Ľ–ĺ–Ĺ—Ź—ā –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā –∑–į –ļ—Ä–į–Ļ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł, –į —ā–ĺ—á–ļ–ł—ā–Ķ –Ľ–Ķ–∂–į—Č–ł –ł–∑–≤—ä–Ĺ –Ņ—Ä–Ķ–ī–Ķ–Ľ–ł—ā–Ķ –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ, –ļ–Ľ–ĺ–Ĺ—Ź—ā –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā —Ā–Ľ–Ķ–ī –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –ł—ā–Ķ—Ä–į—Ü–ł–ł.
–ü—Ä–ł–Ī–Ľ–ł–∑–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ
–ź–ļ–ĺ —Ā–Ķ –ł–∑—Ā–Ľ–Ķ–ī–≤–į –≥—Ä–į—Ą–ł–ļ–į—ā–į –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–į –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, —Č–Ķ –∑–į–Ī–Ķ–Ľ–Ķ–∂–ł—ā–Ķ —Ā—Ä–Ķ–ī –ľ–Ĺ–ĺ–≥–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ—ā–ĺ –ĺ—ā —Ü–≤–Ķ—ā–ĺ–≤–Ķ –ł —Ą–ĺ—Ä–ľ–ł, –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł, –ļ–ĺ–ł—ā–ĺ —Č–Ķ –≤–ł –Ĺ–į–Ņ–ĺ–ľ–Ĺ—Ź—ā –ł –Ĺ–į —Ą—Ä–į–≥–ľ–Ķ–Ĺ—ā–ł –ĺ—ā –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į—ā–į –Ĺ–į –Ė—é–Ľ–ł–į, –į –ł –Ĺ–į —Ā–į–ľ–į—ā–į —Ą–ł–≥—É—Ä–į –Ĺ–į —Ą—Ä–į–ļ—ā–į–Ľ–į –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā. –Ę–Ķ–∑–ł –Ķ—Ą–Ķ–ļ—ā–ł –Ĺ–į —Ā–į–ľ–ĺ–Ņ–ĺ–ī–ĺ–Ī–ł–Ķ —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į—ā, –ľ–į–ļ–į—Ä –ł –Ĺ–Ķ –Ī–Ķ–∑ –ī–Ķ—Ą–ĺ—Ä–ľ–į—Ü–ł–ł, –Ĺ–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ľ–į—Č–į–Ī–Ĺ–ł –Ĺ–ł–≤–į.
 |
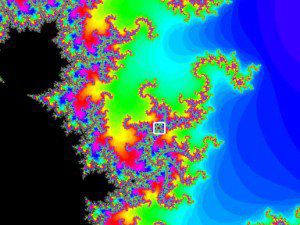 |
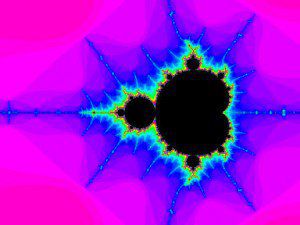
| –†–ł—Ā 1. –ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā. –ü–ĺ —Ö–ĺ—Ä–ł–∑–ĺ–Ĺ—ā–į–Ľ–Ĺ–į—ā–į –ĺ—Ā —Ā–į —Ä–Ķ–į–Ľ–Ĺ–ł—ā–Ķ —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł Cx, –į –Ņ–ĺ –≤–Ķ—Ä—ā–ł–ļ–į–Ľ–Ĺ–į—ā–į –ĺ—Ā - –ł–ľ–į–≥–ł–Ĺ–Ķ—Ä–Ĺ–ł—ā–Ķ —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł Cy | –†–ł—Ā 2. –£—á–į—Ā—ā—ä–ļ –ĺ—ā –≥—Ä–į–Ĺ–ł—Ü–į—ā–į –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, (–Ĺ–į —Ä–ł—Ā.1 –Ķ –ĺ–≥—Ä–į–ī–Ķ–Ĺ–ĺ –≤ –Ī—Ź–Ľ –ļ–≤–į–ī—Ä–į—ā) —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ 17 –Ņ—ä—ā–ł. |
 |
 |
| –†–ł—Ā 3. –£—á–į—Ā—ā—ä–ļ –ĺ—ā –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, (–Ĺ–į —Ä–ł—Ā.2 –ĺ–≥—Ä–į–ī–Ķ–Ĺ –≤ –Ī—Ź–Ľ –ļ–≤–į–ī—Ä–į—ā) —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ 13 –Ņ—ä—ā–ł | –†–ł—Ā 4. –£—á–į—Ā—ā—ä–ļ –ĺ—ā –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, —Ā–ł–ľ–Ķ—ā—Ä–ł—á–Ķ–Ĺ —Ā–Ņ—Ä—Ź–ľ–ĺ —Ä–Ķ–į–Ľ–Ĺ–į—ā–į –ĺ—Ā, (–Ĺ–į —Ä–ł—Ā.1 –ĺ–≥—Ä–į–ī–Ķ–Ĺ –ĺ—ā –∑–Ķ–Ľ–Ķ–Ĺ –ļ–≤–į–ī—Ä–į—ā) —ā–ĺ—á–Ĺ–ĺ –Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –Ĺ–į —Ü–Ķ–Ľ–ł—Ź —Ą—Ä–į–ļ—ā–į–Ľ |
–ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –∑–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ā—ā–Ķ–Ņ–Ķ–Ĺ–Ĺ–ł –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ–ł
–ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, –ļ–ĺ–Ķ—ā–ĺ –Ĺ–į–Ļ-—á–Ķ—Ā—ā–ĺ —Ā–Ķ –Ņ–ĺ–ļ–į–∑–≤–į¬†–Ķ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –ĺ—ā 2-—Ä–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ. –Ę—É–ļ –ľ–ĺ–∂–Ķ –ī–į –≤–ł–ī–ł—ā–Ķ –Ņ—Ä–ł–ľ–Ķ—Ä–ł –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā –∑–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł –∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ–Ĺ–ł—Ź –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ.
 |
|||||||||||||||
| 1 | 1.2 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.3 | 2.5 | 3 | 3.5 | 4 | 5 | 6 | 7 | 10 |
–ė–Ĺ—ā–Ķ—Ä–į–ļ—ā–ł–≤–Ĺ–ĺ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā, –Ė—é–Ľ–ł–į –ł –Ě—é—ā–ĺ–Ĺ
–ě—Ā–Ĺ–ĺ–≤–Ĺ–ł –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź –ł –Ľ–Ķ–ļ—Ā–ł–ļ–į
- –ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ł —á–ł—Ā–Ľ–į
- –ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į
- –∑–į–Ņ—ä–Ľ–Ĺ–Ķ–Ŗ嬆–ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į
- –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ—ā–ĺ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –Ė—é–Ľ–ł–į
- –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–į —Ą–ł–≥—É—Ä–į
- —Ö–ĺ–ľ–Ķ–ĺ–ľ–ĺ—Ä—Ą–Ķ–Ĺ
- –Ņ—Ä–į—Ö –Ĺ–į –§–į—ā—É
- –í—Ä—ä–∑–ļ–į—ā–į –ľ–Ķ–∂–ī—É –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į—ā–į –Ĺ–į –Ė—é–Ľ–ł–į –ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā
- –ö—Ä–ł—ā–Ķ—Ä–ł–Ļ –∑–į –Ķ–ī–Ĺ–ĺ—Ā–≤—ä—Ä–∑–į–Ĺ–ĺ—Ā—ā –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –Ė—é–Ľ–ł–į
- –ú–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–ĺ –Ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā
- –ď–į—Ā—ā–ĺ–Ĺ –Ė—é–Ľ–ł–į
- –ü–ł–Ķ—Ä –§–į—ā—É
- –Ď–Ķ–Ĺ–ĺ–į –ú–į–Ĺ–ī–Ķ–Ľ–Ī—Ä–ĺ—ā
–ė–∑—ā–ĺ—á–Ĺ–ł—Ü–ł:
Fractal Geometry, Yale University, Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger
–í–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ –≤–ĺ —Ą—Ä–į–ļ—ā–į–Ľ—č, –®–į–Ī–į—Ä—ą–ł–Ĺ –ź.–ź.
Fractals: Useful Beauty (General Introduction to Fractal Geometry)
–Į–∑—č–ļ —Ą—Ä–į–ļ—ā–į–Ľ–ĺ–≤, –•–ź–†–Ę–ú–£–Ę –ģ–†–ď–ē–Ě–°, –•–ź–ô–Ě–¶-–ě–Ę–Ę–ě –ü–ź–ô–Ę–ď–ē–Ě, –Ē–ė–Ę–ú–ź–† –ó–ź–£–ü–ē
–ö—Ä–į—Ā–ł–≤–į—Ź –∂–ł–∑–Ĺ—Ć –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —á–ł—Ā–Ķ–Ľ,¬†–°–ļ–Ľ—Ź—Ä–Ķ–≤—Ā–ļ–ł–Ļ –ē. –°.
–Ę–Ķ–ľ–į: –ĺ—Ā–Ĺ–ĺ–≤—č —ā–Ķ–ĺ—Ä–ł–ł —Ą—Ä–į–ļ—ā–į–Ľ–ĺ–≤
–Ē–ł–Ĺ–į–ľ–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—Ä–į–ļ—ā–į–Ľ—č, –ē–≤–≥–Ķ–Ĺ–ł–Ļ –ē–Ņ–ł—Ą–į–Ĺ–ĺ–≤
–ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–Ķ —á–ł—Ā–Ľ–į, –ē–≤–≥–Ķ–Ĺ–ł–Ļ –ē–Ņ–ł—Ą–į–Ĺ–ĺ–≤


























–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
YKoshev
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ