
Може ли биологията да използва такъв математически апарат като физиката например? Според Жак Дюме (Jacques Dumais), от чилийския университет Адолфо Ибанес, и Етиен Кутюрие (Etienne Couturier), от Парижкия университет Дидро, отговорът е категоричен -да, може.
"Теоретичната биология е все по-близо до теоретичната физика - където математиката е достатъчно формализирана така, че да може да предвиждате неща, които никога не са били наблюдавани или измерени", казва Дюме. Те се надяват да разкрият математически описания на биологични процеси и тези биологични закони да им позволят да предсказват по-рано неизвестни явления, подобно на великите прозрения, които прави теоретичната физика.
Разделяй и владей
На Британския колоквиум за приложна математика, проведен от 20 март до 2 април в Кеймбридж Дюме представя пример за възможностите на математиката в биологията - геометрията на клетъчното делене на растителните клетки. Това не е нова област на изследвания. През 19 век двама биолози предлагат правила за клетъчното делене.
През 1875 г. Юлиус фон Саш (Julius Von Sachs) представя две правила:
- когато една клетка се разделя, тя създава две дъщерни клетки с равни размери;
- новите клетъчните стени сключват със старите клетъчни стени ъгли от 90 градуса.
Около десетилетие по-късно Лео Ерера (Léo Errera) предлага друго правило: че новата стена, създадена от делящите се клетки е възможно най-малка. Всъщност, последното правило имитира сапунените мехури, чиято повърхност се стреми към минимум площ.
Дюме и колегите му са успели да облекат във формули тези правила на растежа и доказват, че само две от тях са необходими - правилото, че новата стена се среща със старите клетъчните стени под ъгъл 90о , следва от другите две.
Екипът на Дюме са приложили своя модел за растеж и делене на клетките върху Coleochaete, просто плоско водорасло, чиито клетки нарастват и се делят по външния периметър на близка до кръг област. Всяка външна клетка има формата на пресечен клин, което улеснява изследователите за точното математично представяне на тези клетки.
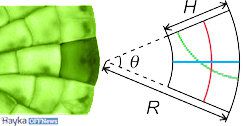 Те описват формата на всяка клетка с ъгъла θ между двете прави стените на клетката, чието продължение се среща в центъра на растението, и съотношението H/R на дължината на клетката H върху радиуса R на цялото растение до този момент.
Те описват формата на всяка клетка с ъгъла θ между двете прави стените на клетката, чието продължение се среща в центъра на растението, и съотношението H/R на дължината на клетката H върху радиуса R на цялото растение до този момент.
Клетки растат по дължина и се разделят по един от следните три начина: по протежение на клина (посочено в синьо на схемата вляво), напряко на клина (в червено), а понякога през единия ъгъл (в зелено).
Това геометрично описание на възможните клетъчни форми и двете правила на делене облечени в математически формули дават такива прогнози за растежа на Coleochaete, които съвпадат с реалните.
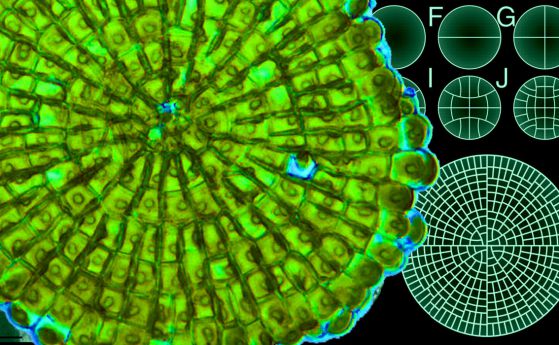
 Вляво е микроструктурата на клетъчния модел на Coleochaete (снимка: life.umd.edu), вдясно е математически предсказан клетъчен модел(изображение: PRECISION GRAPHICS)
Вляво е микроструктурата на клетъчния модел на Coleochaete (снимка: life.umd.edu), вдясно е математически предсказан клетъчен модел(изображение: PRECISION GRAPHICS)
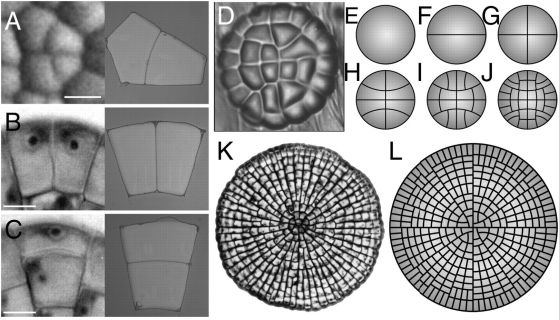 Илюстрация към работата на Дюме - Universal rule for the symmetric division of plant cells
Илюстрация към работата на Дюме - Universal rule for the symmetric division of plant cells
Притегляне към фиксирани точки
Дюме и колегите му прогнозират клетъчното делене и растеж на Coleochaete и други растения като определят бъдещето на всяка клетка като част от динамична система, като нещо, което се променя с течение на времето. Те разглеждат целия набор от геометрични форми, които една растителна клетка може да приема, а след това й прилагат математическите правила на клетъчно делене, за да предскажат как формата на тази клетка и нейните дъщерни клетки ще се променят с течение на времето.
Например, за динамичната система за Coleochaete, всички клетки трябва да попадат в двумерното пространството на възможните клетъчни форми. Това пространство се изобразява с две оси: вертикална ос за съотношението радиус/височина ( H/R ) и хоризонтална ос за ъгъла на клина ( θ ). Клетката расте и се разделя, а произтичащите от това промени в нейната форма и нейните дъщерни клетки очертават пътя през пространството на възможните форми. Повечето широки клетки ще се делят по продължение на клина (в синьо), повечето дълги клетки напряко на клина (червено). След това те ще се уголемяват, движейки се нагоре по продължение на оста H/R, докато не се разделят отново.
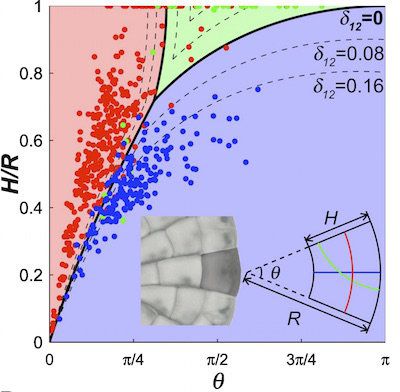 Динамична система на растежа и деленето на клетките Coleochaete. (Снимка: J. Dumais)
Динамична система на растежа и деленето на клетките Coleochaete. (Снимка: J. Dumais)
За всички клетки, формата на техните последващи дъщерни клетки ще се стреми към формата, която се описва от границата на синята и червена област. Клетките разположени в близост до началото на координатите в това пространство имат много малък ъгъл и височина, която е малка в сравнение с радиуса на растението. Не е изненадващо, тук ще имат подобна, приблизително еднородна форма.
В динамичната система на клетъчните форми на Coleochaete ще клонят към определена форма, защото има привличане на фиксирана точка.
Фиксирана точка на динамичната система е състояние, при което, ако един елемент от системата го да достигне, то тогава той остава завинаги в това състояние.
В случая на растителните клетки, фиксираната точка е такава форма, която, ако една клетка я достигне, то всяка една от нейните дъщерни клетки ще има същата форма. Това се случва, когато прилагането на двете правила на делене води до някакъв вид самоподобие между майчината и дъщерната клетка.
Изследователите съставили уравненията, описващи тези динамични системи и намерили фиксираните точки за широко разнообразие от растения, където централната клетка, наречена апикална клетка, е главната точка на растежа, непрекъснато делейки се и произвеждайки дъщерни клетки. Тъй като се произвеждат все повече и повече клетки, ранните дъщерни клетки се придвижват далече от апикалната клетка и започват и те да се делят. Тези пакети от клетки, всички потомци на конкретна дъщерна клетка, винаги запазват отпечатъка на формата на първоначалната дъщерна клетка.
Като разглеждат всички възможни форми, които апикалните клетки биха могли да приемат, Дюме и колегите му, установяват пет възможни фиксирани точки, при които правилата за разделяне създават дъщерни клетки с идентична форма. Всяка една от тези фиксирани точки се различава с броя на страните си.
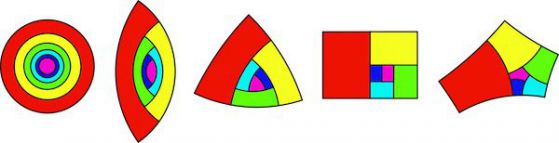
Петте възможни фиксирани точки за клетъчно делене на апикални клетки.
Лилавата фигура е апикалната клетка, която продължава да бъде централна главна точка на растежа, като същевременно продължава да се дели. Другите цветни фигури са дъщерните клетки, които се придвижват все по-далече от апикалната клетка, която произвежда все повече дъщерни клетки. Червената фигура е най-старата от тези дъщерни клетки, показани на схемите, тъмносините са най-младите. Ако правоъгълникът ви изглежда познато, това е така, защото има пропорциите на формата A на листовете хартия.
Биологичният Хигс бозон?
Учените познават някои растения, които имат клетки, отговарящи на тези фиксирани точки.
"Вече сме виждали 2- и 3-странни клетки", - казва Дюме. - "Не бях виждал 4-странни клетки [преди нашата прогноза], но вече открихме два примера."
"Остава само да се намери в природата неуловимата 5-странна фиксирана точка. Може би това ще е Хигс бозонът на биологията, прогнозиран математически, преди да се наблюдава в природата? Може би, но най-вероятно няма", казва Дюме.
Малко вероятно е, че някога ще видим клетка с такава форма в природата, както смятат учените, 5-странната клетка не може да бъде стабилна фиксирана точка при реални биологични условия.
При другите четири фиксирани точки дъщерните клетки, образувани като близки по форма на съответните фиксирани точки, си остават близки по форма на тези фиксирани точки. За разлика от първите 4 модела, дъщерните клетки, които по форма се отклонят дори малко от форма на 5-странната фиксирана точка, може да се окажат с много по-различна форма.
Елегантната простота на този математически модел на клетъчното делене е чудесен пример за успешен подход в теоретичната биология.
"В биологията, за разлика от механиката на флуидите или физиката, има много "шум" и ненадеждни данни", казва Кутюрие. "Ако направите сложен модел, той често няма да работи, няма да е достатъчно стабилен. По принцип, ако искате да направите нещо смислено, трябва да отделите много време, за да намерите нещо, което може да се вмести в прост модел."
За биологията и хаотичните данни, които предоставя, трябват прости инструменти.
Това може да направи нейната област още по-привлекателна за математиците, за които колкото е по-прост и елегантен един модел, толкова по-добър. Ако специалистите по теоретична биология успеят да приведат биологичните процеси в такива красиви математични модели, Дюме вярва, че това ще донесе големи прозрения за самата биология. "Биологията ще спечели много. Това, което липсва в момента в биологията е рамка, която да обясни или да организира цялата информация, която имаме."
И точно както теоретичната физика успешно предсказва съществуването на фундаментални частици, като бозона на Хигс, преди експерименталното им потвърждение, така може да очакваме от теоретичната биология да разкрие нови вълнуващи хоризонти в природата около нас.

















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон