
За симетрията и в частност за тази на кристалите говорихме в серия от публикации: Симетриите като групи, Видове симетрия, Кристалите-тържеството на симетрията.
За симетрия при аморфните въобще не може да се говори - молекулите им са разпределени напълно произволно.
Кристалите са строго подредени, осите на симетрия могат да сключват ъгли само 180°, 120°, 90° и 60°. Симетрия от 5-ти порядък и по-висша от 6-ти е забранена.
И така: при кристалите се наблюдава осева симетрия само от 1, 2, 3, 4 и 6-ти ред. Няма кристални решетки със симетрия от 5-ти ред и над шести ред, но в животинския свят, симетрия от 5-ти порядък е не рядко срещана - и при растенията, и при едни от най-развитите безгръбначни и братовчеди на първите гръбначни организми, бодлокожите - морските звезди и таралежи..
Възможно ли е да съществува нежива материя със симетрия от 5-ти ред?
Кристален или аморфен
Доскоро се смяташе, че всички тела в природата може да бъдат разделени на две коренно противоположни, рязко различаващи се групи:
|
Кристални тела
|
Аморфни тяла
|
|---|---|
 Кристалната решетка на кварц SiO2 Кристалната решетка на кварц SiO2 |
 Молекулярна схема на стъкло SiO2 Молекулярна схема на стъкло SiO2 |
| Илюстрации: Sólido amorfo | |
|
подредена структура, повтаряща се в в трите пространствени измерения навсякъде в материала
|
липсва подредена структура, без определени форми и повърхности.
|
|
анизотропни - имат различни свойства в различни направления
|
изотропни
|
|
точно определена температура на топене или кристализация
|
няма точна температура на топене, а материалът постепенно се размеква.
|
Това разделение на структурата на твърдите вещества е продължило почти до края на ХХ век, когато е открит един не съвсем подреден кристал - квази-(от лат. quasi - мним, не съвсем) кристал - междинна форма между аморфна и кристална и със "забранена" симетрия - 5 и над 6-ти порядък и с непериодична структура.
Квазикристалът на един не квази-учен
На 8 април 1982 г. израелският учен Даниел Шехтман (Dan Shechtman) и негови сътрудници извършват рутинно изследване на бързоохлаждаща се сплав от алуминий и манган Al6Mn. Разглеждайки получената дифракционна картина видяли, че съдържа типичните за кристалите ярки максимуми (рефлекси), но и те били подредени в ротационна симетрия от 5-ти порядък, което противоречало на класическата кристалография и смятано досега за невъзможна в триизмерна периодична решетка.
"Казах на всеки, който е готов да слуша, че имам материал с петоъгълна симетрия. Хората просто ми се изсмяха."
Заради еретичните си идеи, Шехтман бил изритан от университетската изследователска група и не намира нова група. Премества се в Израел, където се опитва да намери някой, който да публикува изследванията му. Статията първо отхвърлена, накрая е публикувана през ноември 1984 г., но резултатите му са обект на скептицизъм и насмешка. Двойният нобелов лауреат Линус Паулинг заявил:
"Дани Шехтман говори глупости. Няма такова нещо като квазикристали, има само квази-учени".
По-късно обаче били открити други квазикристали с различен състав и различни симетрии - от пети, седми и по-висши редове. Вече по-прецизни експерименти разсеяли всякакви съмнения и доказали, че симетрията на квазикристалите е на всички нива, чак до атомите . Това е наистина нова структура на организация на материята.
 |
 |
| Дифракционна електронна картина на квазикристал Ho-Mg-Zn. Кредит: Ron Lifschitz, Cornell University | Кристал на сплав Ho-Mg-Zn (холмий, манган, цинк) - икосаедричен квазикристал във форма на додекаедър, който е дуален на икосаедъра. Кредит: stanford.edu |
През 1992 Международният съюз по кристалография променя своето определение на кристал, разширява го като резултат от усилията на Шехтман, като признава възможността за периодично или непериодично подреждане.
В края на краищата Шехтман "е принудил учените да преразгледат своята концепция за самата същност на материята", казва Шведската Академия са присъждане на нобелови премии и през 2011г, той получава Нобелова награда за химия..
След първият, открит от Дан Шехтман квазикристал (наречен шехтматин), са открити още стотици други, най-често многометални сплави и някои полимери: алуминиеви сплави (Al-Li-Cu, Al-Mn-Si, Al-Ni-Co, Al-Пд-Mn, Al-Cu-Fe, Al-Cu-V и т.н.), и множество други композити (Cd-Yb, Ti-Zr-Ni, Zn-Mg-Хо, Zn-Mg-SC-Ag-Yb, Pd-U-Si и др.).
Известни са два вида квазикристали:
|
 Снимка с електронен микроскоп на силициев композит - икосаедричен квазикристал: Quasicrystals from nanocrystals ,Alfons van Blaaderen (чертичката е 2 микрона) Снимка с електронен микроскоп на силициев композит - икосаедричен квазикристал: Quasicrystals from nanocrystals ,Alfons van Blaaderen (чертичката е 2 микрона) |
Опити за обяснение
Да се обясни растежа и стабилността на квазикристалите е невъзможно със средствата на класическата кристалография. Липсва транслация, но как се обясняват белезите на все пак някаква подреденост?
Установено е, че съотношението на елементите на квазикристалите е в златна пропорция, което съчетано с петоъгълната симетрия натрапва приликата с "мозайките на Пенроуз" и както казва Питър Дж. Лу, от Харвардския университет като че ли ислямските математици и художници са открили схемата на квазикристалите преди стотици години.
 Атомен модел на повърхността на квазикристал (Al-Pd-Mn).Снимка: wikipedia Атомен модел на повърхността на квазикристал (Al-Pd-Mn).Снимка: wikipedia |
 Мозайка на Пенроуз "двата ромба". Илюстрация: quadibloc.com Мозайка на Пенроуз "двата ромба". Илюстрация: quadibloc.com |
 Фрагмент от средновековна ислямска мозайка, Исфахан, Иран. Снимка: math.ucr.edu Фрагмент от средновековна ислямска мозайка, Исфахан, Иран. Снимка: math.ucr.edu |
|
Въпреки, че непериодичните мозайки на Пенроуз са се появили като математическа игра, те са впрегнати да обяснят това ново явление. Тази теория приложил към кристалографията Алън Маккей. Той поставил атоми във възлите на мозайката на Пенроуз, изчислява картината на дифракция и получава модел със симетрия от десети ред, подобен на квазикристалните. Фрагменти на атомната структура на квазикристалите могат да бъдат тримерни аналози на мозайките на Пенроуз - остри и тъпи ромбоедри с ъгли при върховете 63,43° и 116,57°, из които може да се сглоби многостен, наречен триаконтаедър със симетрия 53m. |
 Обемна мозайка на Пенроуз. Снимка: Livejournal Обемна мозайка на Пенроуз. Снимка: Livejournal |
В обемния си вариант мозайката на Пенроуз може да е съставена от икосаедри - дванайсетостени с триъгълни стени, като на всеки връх се срещат пет триъгълници, от където идва и симетрията от 5-ти порядък.
Проекция от 6-тото измерение
Преди да продължим, ви препоръчвам да прегледате раздел Четвъртото измерение в този сайт, ако досега не сте се сблъсквали с идеята за пространства с размерност над обичайната ни.
Тъй като да се опишат квазикристалите в 3D пространството не е толкова лесно, колкото при нормални кристални структури, на помощ ни идват и по-висшите пространства.
За да се определят нормалните кристали са достатъчни три цели числа (индекси на Милер), отразяващи триизмерната транслационна периодичност на структурата.
Необходимостта от n вектора съответства на nD-мерно пространство. С други думи, в пространство с по-висока размерност от трета, квазикристалите може да се опишат периодично.
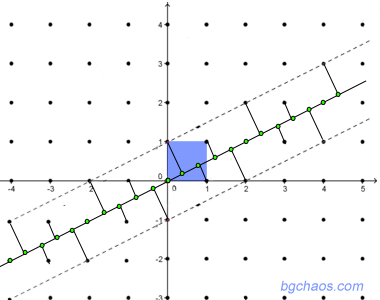 |
Ще си обясним това с пример от една по-ниска размерност. Представете си една двумерна периодична решетка Да прекараме ос и проектираме върху нея точките, които попадат в ивицата около оста. Ако наклонът й някаква част от периода, да речем 1/2, то проекциите ще отразяват периодичната структура на двумерната решетка. |
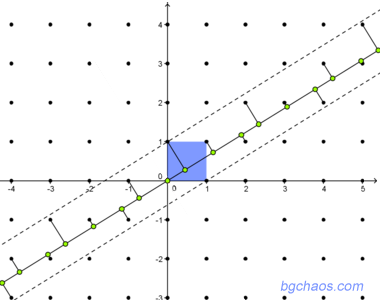 |
Но ако наклонът е някакво ирационално число като π (3.1415...) или златното сечение φ=1.618... - често срещано при кристалите, тогава проекциите ще са една непериодична едномерна решетка. Последователността на тези стойности изглежда повече или по-малко хаотична - липсва транслационна симетрия, ако не разширим пространството до две измерения, тогава всичко става ясно: нашият едномерен квазикристал е само част от проекцията на една периодична квадратна мрежа. |
И така, за да се зададат целочислени индекси на квазикристалите са необходими най-малко 5 линейно независими вектори за многоъгълните квазикристали и 6 за икосаедрични квазикристали.
Тоест необходимо е пет- или шестмерно пространство, в което квазикристалите са периодични. При проекция в тримерното пространство периодичността изчезва и се превръща в необичайната петоъгълно-симетрична дифракционна картина.
|
Вдясно е модел на хексаракт ( 6-мерен куб ), представен като изпъкналата обвивка в 3D. Тялото се нарича ромбоичен триаконтаедър (30-тостен), диагоналите на стените му са в златна пропорция: 1: φ . Тази 3D-проекция се използва, за да се разбере структурата на квазикристалите. 3D базисните вектори [U, V, W] са: U = (1, φ , 0, -1, φ , 0)V = ( φ , 0, 1, φ , 0, -1)W = (0, 1, φ 0, -1, φ )Това тяло има 192 ръба с дължина единица, 64 върха, центрове на петоъгълна симетрия по една ос и шестоъгълна симетрия по друга ос. |
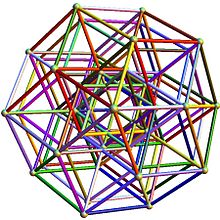 Илюстрация: wikipedia Илюстрация: wikipedia |
Истинската квазипериодична структура в 3D-физическото пространство може да бъде получена чрез подходящи техники за проекция и сечение. Така че е достатъчно да се определи една единична клетка с nD-структура, чието съдържание се състои от "хиператоми", по аналогия на атомите в една нормална единична клетка в кристалите. Това ни позволява да се опише цялата структура на квазикристалите с ограничен набор от параметри.
Оказва се, че картината на мозайката на Пенроуз при квазикристалите се получава като сечение на пет- и шестмерна кубична решетка с наклонена равнина.
Не всички приемат това толкова сложно обяснение - то обяснява дифракционната картина, но не дава отговор на въпроса как локалните междуатомни взаимодействия може да стабилизират квазикристала и установят периодичност на далечни разстояния в едно хиперпространство.
В същото време, при растежа на кристала от стопилката, атомите се присъединяват към повърхността на зародиша по някакъв закон, който има локален характер. Как атомите "знаят" (заради естеството на междуатомните си взаимодействия) какви местната конфигурации може да образуват и какви не може за да се формира в двумерния случай мозайка на Пенроуз.
 Илюстрация: discovermagazine
Илюстрация: discovermagazine
Харвардският физик Ерик Хелър ни напомня за вълновите свойства на материята в субатомни мащаби. Той генерира компютърно взаимодействието на няколко плоски вълни, а резултатът е картина на квазикристал, която оцветена виждаме горе.
| Представям и две анимации, първата приписвана на Джейсън Дейвис (Jason Davies), но Кийгън (Keegan) представя в блога си, кода на Java. |  Илюстрация: Джейсън Дейвис Илюстрация: Джейсън Дейвис |
 Илюстрация: michaelerule Илюстрация: michaelerule |
Някои смятат, че квазикристалът е всъщност микрокристално състояние, при което веществото се групира в икосаедрични клъстери, произволно свързани помежду си, а кристалографски ограничения върху такива опаковки няма, защото клъстерът може да има каквато и да е форма - той няма нужда да запълва с решетката си безкрайни пространства. Въпросът остава открит.
Квазизаразата е от космоса
От 1984 г. са получени в лабораторни условия повече от 100 квазикристали и се смяташе, че естественото им образуване е невъзможно, тъй като структурата им е изключително нестабилна.
 Метеоритът от Чукотка - единственият засега природен образец на квазикристал. Снимка: Paul J. Steinhardt
Метеоритът от Чукотка - единственият засега природен образец на квазикристал. Снимка: Paul J. Steinhardt
Природни квазикристали са намерени в планините Коряк в Чукотка, в Даления Изток на Русия. Човекът, който пръв е намерил проба през 1979 г. е Валери Крячко, който е бил изпратен да търси платина в глинестото корито на приток на река Хатирка. Той не успял да намери платина, но се върнал с "няколко скални отломъка с метални фази". Пробата квазикристал е сред тях. Тези първи находки предизвикали вълна на интерес към далечните планини. .
През 2010 г. Пол Дж.Щайнхард ( Paul J. Steinhardt) изказал предположението, че камъкът, в който е намерен квазикристала е метеорит. Дори е успял да идентифицира метеорита - въглероден хондрит CV3, много древен метеорит, образуван заедно със Слънчевата система преди около 4,5 милиарда години
Тази проба се съхранява сега в Природно-историческия музей във Флоренция. Как е стигнала до там изяснява следствие с участващи "тайни дневници, контрабандисти, злато златотърсачи и мечки".
 Река Хатирка. Снимка: PeterSobolev
Река Хатирка. Снимка: PeterSobolev
В едно приключение, с цената на много усилия и премеждия екип от десет учени, начело с италианския учен Лука Бинди и Пол Щайнхард стигат до планината Коряк и събират още проби, които съдържат естествени квазикристали и всичките се оказали с метеоритен произход.
Още необикновени неща за квазикристалите
Физичните свойства на квазикристалите са също така необикновени, както и техните структури. Въпреки че са метални сплави, те имат рекордни топло- и електроизолационни характеристики. В сравнение със специалните сплави квазикристалите имат много по-висока твърдост и механична устойчивост , но са твърде крехки, поради което най-често се прилагат под формата на покрития. Тези покрития имат нисък коефициент на триене, слабо се мокрят и са с изключително висока корозионна устойчивост.
Квазикристалите имат доказана биологична съвместимост заради почти напълната им химична и имунна пасивност. Това ги прави идеални за имплантиране с дълготрайна поносимост от живия организъм.
Учените си задават смелия въпрос дали точно квазикристалите не са липсващото звено в прехода между физичните и биологичните структури, между живата и неживата материя? В светлината на метеоритния произход на единствените намерени в природата квазикристали, обаче излиза на преден план отново теорията за панспермията, която ни насочва към идеята за извънземния произход на Живота на Земята.
Теория на конспирацията
Квазикристали от Розуел
Вероятно сте чували, че кристалите са живи, лекуват, че е възможен и силициен живот и т.н. Мистерията около квазикристалите обаче е още по-сгъстена. В главата "Сакралната геометрия в квантовата реалност" в книгата си "Божествения Космос", Дейвид Уилкок намеква, че на Шехтман, който по това време работи в лаборатория към ВВС на САЩ, му е било позволено да “открие“ квазикристала.
Идеята е, че квази кристалите са, заедно с тефлона и кевлара, един от продуктите на реверсивната технология (разработка по готово изделие). Ако има някой, който не е чувал за Розуел, нека последва линка.
Житните кръгове и квазикристалите
|
Ето на какво попаднах в сайта на Crop Circles Research Foundation Този житен кръг се е появил на плантация "Юбилейна" в Уилтшир, Великобритания на 15 август, 2011г. Впечатлява с дизайна и съвършенството на изпълнението си. Пшеницата в дебелия пръстен е оформена в повтарящ се мотив, напомнящ на течаща вода в поточе Но това, което виждаме в центъра е най-поразително: дифракционна картина на икосаедричен квазикристал на Ho-Mg-Zn. Това, което трябва да ви напомня обаче е това, че Нобелова награда на Дан Шехтман е обявена пред света на 5 октомври 2011, 51 дни след появата на кръга. |
 |
 Снимка: Bert Janssen Снимка: Bert Janssen |
Източници:
Chemistry Nobel: Quasicrystals – Israeli Found New Form of Matter Imagined in Islamic Art
Кристалл сомнения , С. М. Комаров, кандидат физико-математических наук
Ю. Х. Векилов, М. А. Черников. Квазикристаллы. Успехи физических наук,
Generalized Penrose Tilings as Projections, JT Halbert
Two-dimensional tiling in three-dimensional space, Antony J. Bourdillon
Гуртов В.А., Осауленко Р.Н./ Научный редактор Л.А. Алешина Физика твердого тела
Квазикристаллы, livejournal
Божествения космос, Дейвид Уилкок
О “золотом” квазикристалле
Утрата симметрии: Мозаики Пенроуза и квазикристаллы
Quasicrystals , Steffen Weber
Higher Dimensions, Klein Project Blog
Aperiodic Crystals: From Modulated Phases to Quasicrystals , Ted Janssen, Gervais Chapuis, and Marc de Boissieu
Mathematical Details, deBruijn
























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Доколко съвместими са минерално-суровинният отрасъл и чистата околна среда?
Козон
Мистериозен череп на гръцки хоминин е датиран на поне 286 000 години
Peter Petrov
След многократни експлозии нов тест за мегаракетата на Мъск
поп Дръвчо
Гледайте за първи път на живо как новооткритият "междузвезден посетител" 3I/ATLAS се устремява към нас