Задачи за плочкаджии и математици
Английският математик Дж. Х. Харди (Godfrey Harold Hardy), в книгата си "Апология на математиката" е написал: "Математикът, също както художника или поета, е създател на образи и ако неговите образи са по-трайни от техните, то е, защото са изградени от идеи". Този цитат е използвал и Мартин Гарднер за да въведе читателите си в темата за мозайките в популярния си тритомни "Занимателна математика".
|
Край нас е изобилие от този математичен модел - мозайки, паркети, плочници, зидарии, тапети, платове и покривала от всякакъв тип с десени върху тях. В природата от една страна - кожа, листа, люспи, пера, от друга страна - пяна, напукана почва (клетки на Бенар под една или друга форма) - 3D-еквивалент на мозайките - са все начини за решаване на задачата за опаковката за равнината или пространството. |
 |
| Шестостенни базалтови структури при Пътя на гигантите (Giant's Causeway), Северна Ирландия. Снимка: wikipedia |
Това е и икономическа задача - максимум резултат с минимум енергия и материал - да се скрои плат без много остатъци, да се покрие тротоара по-ефективно, с минимум разтвор между плочките - задача, която между впрочем, пчелите са решили блестящо. Изкуших се да ви представя една малка галерия от образци на природни мозайки с различим и не толкова различим произход.
Надявам се, да ви е забавно да откриете сами кое от кого е: пчелна пита, риба, боа, кора, царевица, жираф, шишарка, ананас, морска звезда, крокодил, слон, паун, растението Aeonium, напукана земя и един странен бозайник, панголин, чиято кожа се обзалагам, че няма да познаете.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
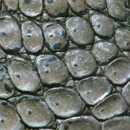Забележете, че тази задача е изпълнена по сходен начин при доста отдалечени видове. Това е резултат от решаването на сходни задачи при сходни условия - законите на геометрията важат за всички. Тези мозайки напомнят и на някои от нашите, човешки практични изобретения - зидария, настилки, керемиди, брони.
Задачата за изпълване на пространството с еднообразни фигури е идея, която се е развивала от древните египтяни и гръцките питагорейци до наши дни. Това е идея, която носи дълбокия смисъл за начините на експанзия с дискретни средства, за възможния строеж на веществото и структурата на пространството.
Мозайките са любима тема на холандския художник-математик Ешер и тук може да видите доста от тях. Той е бил вдъхновен от мозайките на арабския дворец Алхамбра (Испания) - и ние ще обърнем малко внимание на тази магия на ислямското изкуство малко по-късно. А преди това - малко геометрия:
Правилните решения
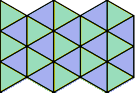
В Кристалите-тържеството на симетрията доказахме, че възможностите са три за запълване на равнина с правилни фигури чрез транслация: това са правилен триъгълник, квадрат и правилен шестоъгълник.
 |  |  |  |
|---|---|---|---|
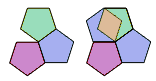
| 3-ти порядък | 4-ти порядък | 5-ти порядък ? | 6-ти порядък |
Положението изглежда безнадежно: правилните петоъгълници имат ъгли 108°. Ако се опитате да наредите плочник с правилни петоъгълници, три не запълват възела до 360°, тъй като 3 х 108° = 324° , а и четири се припокриват, защото 4 х 108° = 432° . Добре, наистина няма други решения, което било ясно още на древните гърци, но какво би станало, ако престъпим лекичко някое от тези ограничения?
Някои полуправилни мозайки
С две и повече различни правилни фигури
|
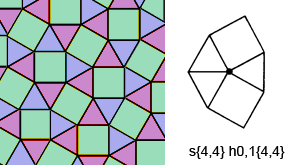
При тези "полуправилни" мозайки два и повече различни правилни многоъгълници се подреждат плътно връх до връх така, че едни и същи фигури да обградят всеки връх в циклично повтарящ се ред. Възможностите са точно 8 и представляват различни комбинации от триъгълници, квадрати, шестоъгълници, осмоъгълници и дванайсетоъгълници. Илюстрации: List of uniform tilings |
 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
Мозайки с не толкова правилни фигури
Има четиринадесет (засега) типа петоъгълници, които запълват плътно равнината
|
Типове от 1 до 5 са открити от K. Райнхард (K. Reinhardt) през 1918г. B. Кершнер (R. B. Kershner) през 1968г. открива типове от 6 до 8 и заявява, че списъкът е пълен, но през 1975г. Р. Джеймс III (R. James III). пише писмо до Мартин Гарднер, описвайки нов тип - 10. Типовете 9, 11-13 са открити от аматьорката-математик Марджъри Райс (M. Rice) през 1976-1977.Тип 14 е открит от Р. Щайн (R Stein) през 1985. Илюстрации: wikipedia |
|
|||||||||||||||||||||
Плочника на Кайро
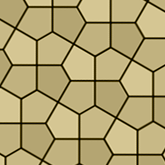
Тип 4 е известната мозайка "плочките на Кайро", защото се говори, че с такива петоъгълни плочки са покрити улиците на Кайро. Облицовка е от петоъгълници, неправилни, страните им не са равни, а техните ъгли са последователно 120°, 120°, 90°, 120°, 90°. Дейвид Бейли е организирал наблюдение в Кайро заедно с трима фотографи на тези знаменити плочници. В страницата си David Bailey's World of Escher-like Tessellations е публикувал резултатите.
|
Тази облицовка може да се разглежда производна на първия тип от колекцията "неправилни мозайки" по-горе, състоящ се от квадрати и равностранни триъгълници. Ако желаете да го проследите, минете с мишката по цифририте под илюстрацията вдясно. За геометричните традиции в ислямското изкуство ще имаме възможност да говорим и по-късно. |
||||||||
Периодични мозайки
Досега разглеждахме само периодични мозайки. Те имат не само повтарящи се мотиви, но и тези мотиви се повтарят през равни интервали и за равнината те трябва да се портарят и по x и по y . Те имат т.н. транслационна симетрия , която развита в пространството моделира кристалните структури.
Тест за периодични мозайки
Кога една облицовка е периодична? Един от начините е да се направи решетка - мрежа от два набора от равномерно разположени успоредни линии.
Тук съм ви дала възможност да си поиграете с различни мозайки и решетки като определите коя решетката пасва на избраната мозайка. Правилно избраната решетка разделя мозайката винаги на еднообразни мотиви. Образуваните от решетката успоредници са периода на решетката.
| Отговорите: | мозайка: | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| решетка: | 1,4 | 1,3 | 2,5 | 6 | - | |
| Това не са единствените възможни решетки - често има по няколко варианта. За последната мозайка обаче няма подходяща решетка - тя е непериодична. | ||||||
Религиозните забрани - стимул за развитието на математиката
Втората Божия заповед: Не си създавай кумири“ е приета абсолютно буквално в исляма като пълна забрана за изобразяване на всякакви живи същества - хора, животни и растения. "Не копирай творенията на Бога, а ги изучавай" - тази повеля е тласнала ислямското изкуство към изобразяване само на абстрактни фигури, но тя е и стимулирала и абстрактното мислене и от там и математиката.
Около 830г., персийският математик Мохамед ибн Муса ал-Хорезми доразвива геометрията на Евклид в обединяваща теория, която ни е известна сега като алгебра (от арабски al-jabara). Неговото име пък е останало до наши дни в думата "алгоритъм".
 Фонтан в гр.Фес, Мароко. Снимка: jannahsteps.com  Мозайка от двореца Алхамбра, Гренада, Испания. Снимка: soler7.com |
Разцветът на ислямската наука от девети до около 13-ти век предава на Европа множество новаторски за нея идеи, някои от тях идващи от Древна Гърция или Индия като десетичната бройна система и нулата. Въвеждането на индуско-арабската бройна система в Европа в началото на 13 век се подкрепя от Леонардо от Пиза (известен като Фибоначи), а за редицата, днес свързана с неговото име е научил от мюсюлманите в Северна Африка. Ислямските мозайки не са просто форма на изкуство или занаят, а и форма на поклонение и духовно преживяване. Алхамбра, мавърски дворец в Гранада, построена около 1300г., има мозайки с най-малко 13 от 17-те възможни групи на симетрия. |
Питър Лу, физик от Харвардския университет, заявява в интервю: "Това е абсолютно зашеметяващо. Те са създали мозайки, които са толкова сложни, че отразяват математика, която ние не сме могли го разберем до последните 20 или 30 години".
 |
 |
 |
 |
 |
| Декоративни решетки от малко известната гробница Paigah в Хайдерабад, понякога наричана "Тадж Махал на Юга".Снимки: Xplore & Xpress, Centre for exploring links between Science , Art & Technology | ||||
 Гробницата на Salim Chisti, каменен релеф, Фатепур Сикри, Индия |
 Гробниците на Саади, керамична мозайка, Маракеш, Мароко |
 Фонтан в гр.Фес, керамична мозайка, Мароко. |
 Imamzeda Darbi Islam, декоративни панели, Исфахан, Иран |
 Тадж Махал, каменна решетка, Агра, Индия |
| Снимка: vishaka jayakumar | Снимка: Susan Reep Photo Art | Снимка: australiantrendsetter | Снимка: math.ucr.edu | Снимки: bgchaos.com |
В тази скромна галерия ви показах някои образци на ислямски мозайки - някои по-прости, с известната ни досега периодичност, но мароканските от Фес и тези от Исфахан са непериодични - едно качество, свързано напоследък с един нов материал, притежаващ подобна непериодична структура, но за това - в следващата тема - "Непериодичните мозайки – хаос и ред в забранени симетрии".
Източници:
Pentagon tiling, wikipedia
CS: Tilings, Islamic Art, Our Retina, Papoulis Sub-Nyquist Theorem
Morphing Tilings
Pentagonal Tesselations, quadibloc
Паркеты, Холодова О.
What are Tilings and Tessellations and how are they used in Architecture?, Jaspreet Khaira
Decorated pottery tile in Museum of Islamic Art ...
Arabic / Islamic geometry
Fun with Mathematics: Tessellations & Islamic Art
Tilings and Tesselations, Science U
An Introduction to Tilings, Cornell Mathematics Занимателна математика, Мартин Гарднер
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
29.03 2015 в 10:55
Последни коментари