Представете си математически инструмент, толкова мощен, че би могъл да свърже сферите на физиката на елементарните частици и космологията така, че да предефинира начина, по който възприемаме архитектурата на Вселената, предлагайки път към дълго търсената "Теория на всичко".
Точно това предлага ново проучване на д-р Клаудия Февола (Claudia Fevola) и д-р Анна-Лаура Сателбергер (Anna‑Laura Sattelberger) от Института по математика в науките "Макс Планк" в Германия.
Чрез прилагане на нововъзникващата област на позитивната геометрия - пресечната точка на физиката и математиката, по-специално физика на елементарните частици, космология и алгебрична геометрия, така и към космологията, учените изследват как нови подходи в алгебричната геометрия биха могли потенциално да изплетат самата тъкан на Вселената.
Публикувано в Notices of the American Mathematical Society, изследването разкрива как многомерни геометрични форми – като амплитуедри и космологични многостени от висши размерности – могат да опишат взаимодействия, вариращи от най-малките частици до най-големите структури в космоса. (вж: "https://nauka.offnews.bg/news/a-190144.html?preview=ok")
Работата демонстрира как инструменти от алгебричната геометрия, теорията на D-модулите и комбинаториката могат да осигурят обединяваща математическа рамка, точно вида пробив, необходим за преодоляване на пропастта между квантовата механика и Общата теория на относителността.
В математиката D-модул е модул над пръстена D от диференциални оператори. Основният интерес на такива D-модули е като подход към теорията на линейните частични диференциални уравнения
"Позитивната геометрия е все още млада област, но има потенциал да повлияе значително на фундаменталните изследвания както във физиката, така и в математиката", казват авторите на изследването в прессъобщение.
"Сега е ред на научната общност да изясни детайлите на тези нововъзникващи математически обекти и теории и да ги валидира."
Търсенето на единство във Вселената
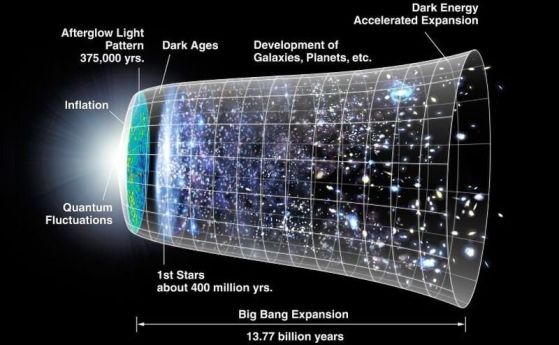
Повече от век физиците се борят с факта, че Вселената изглежда функционира според два различни набора от правила.
От една страна, квантовата теория на полето управлява микроскопичния свят на частиците и силите. От друга страна, Общата теория на относителността елегантно обяснява мащабната кривина на пространство-времето. И двете теории са изумително успешни в своите собствени области. В основата си обаче те остават фундаментално несъвместими една с друга.
Физиците отдавна се стремят да намерят "Теория на всичко" или унифицирана рамка, която може да съгласува гравитацията с квантовата механика. Това търсене е подхранвало десетилетия изследвания в области като теорията на струните или цикличната квантова гравитация.
Въпреки значителния напредък обаче, все още няма подход, който да е успял да обедини всички известни физически закони и явления в единна, всеобхватна "теория на всичко ".
Позитивната геометрия излиза на сцената
Вместо да описва физическите събития, използвайки конвенционалните инструменти на диференциалните уравнения и пертурбативните разширения, позитивната геометрия преформулира взаимодействията по отношение на обеми на форми от висши измерения.
Тези форми – като например амплитуедъра, въведен през 2013 г. – позволяват на учените да изчисляват амплитудите на разсейване на частиците, като измерват обема на внимателно дефиниран геометричен обект, заобикаляйки обичайните изчисления на диаграмата на Файнман.
Д-р Февола и д-р Сателбергер отиват още една крачка напред с този подход. Тяхното проучване показва, че същите геометрични идеи могат да бъдат приложени и към космологични модели – по-специално към ранната Вселена и космическото микровълново фоново лъчение, което все още отеква от Големия взрив. Използвайки космологични политопи (n-мерен многостен), изследователите демонстрират как структурите в самото пространство-време могат да бъдат кодирани на геометричен език.
Какво значение има това за обединението?
Независимо дали частица се движи около колайдер в ЦЕРН или галактика се формира на милиарди светлинни години разстояние, и двете явления могат да бъдат описани с един и същ вид геометрия. Това е силен намек за по-дълбоко единство в природата.
В подкрепа на своя подход, авторите се позовават на богатия апарат на алгебричната геометрия – изучаването на форми, дефинирани от полиномиални уравнения. Те свързват амплитудите на разсейване с "графови полиноми", които могат да се интерпретират като алгебрични многообразия, и използват теорията на D-модулите, за да анализират диференциалните уравнения, които управляват тези системи.
Скица на амплитуедър, представящ взаимодействие между 8 глуонни частици. При използване на диаграмите на Файнман същото изчисление би отнело около 500 страници алгебра. Кредит: Nima Arkani-Hamed
Това, което прави това особено мощно, е начинът, по който тези техники опростяват трудните изчисления, които измъчват физиката на високите енергии. Вместо ръчно да изчисляват хиляди диаграми на Файнман, изследователите могат да се съсредоточат върху идентифицирането на геометричните свойства на един-единствен главен интеграл.
Броят на тези главни интеграли, от своя страна, се определя от топологични характеристики, отново подсилвайки дълбоката връзка между геометрията и физиката.
В областта на космологията подобни интеграли възникват в "модели-играчки", които симулират корелациите между квантовите флуктуации в ранната Вселена. Д-р Февола и д-р Сателбергер обаче демонстрират, че интегралите на тези модели могат да бъдат представени като обеми на геометрично дефинирани многостени.
Още по-забележително е, че остатъците от тези интеграли, които улавят основните характеристики на основната физика, съответстват на лицата на тези форми – допълнително потвърждаване, че позитивната геометрия може да държи ключа към обединението.
Отвъд теоретичните модели към реалността
Въпреки че голяма част от настоящата работа се фокусира върху опростени версии на физическите теории, последиците се простират далеч отвъд абстрактното.
Д-р Февола и д-р Сателбергер са част от проекта за синергийна субсидия на Европейския съвет за научни изследвания, UNIVERSE+, мултинационална инициатива, която има за цел да разработи реалистични геометрични модели, включващи гравитацията и разширяващата се Вселена, проправяйки пътя за истинско обединение.
Това, което отличава това изследване от предишни опити за Теория на всичко, е неговата гъвкавост. Геометрията тук не е просто метафора – тя е изчислителен двигател. Чрез идентифициране на правилните геометрични форми, изследователите могат да получат по-задълбочени познания за природата и да разработят практически методи за решаване на преди това сложни проблеми.
За разлика от Теорията на струните или квантовата гравитация на циклите, които са били обект на десетилетия на критичен анализ и оживени дебати, позитивната геометрия до голяма степен е избягвала широка критика досега. Отчасти това се дължи на факта, че тя все още е сравнително млада и развиваща се рамка – по-скоро обещаващ математически инструментариум, отколкото пълноценна физическа теория.
Освен това, дори в ранните си етапи, позитивната геометрия все още е съпроводена с няколко важни уговорки.
Някои физици предупреждават, че голяма част от настоящата работа се основава на хипотетични модели, които опростяват сложните реалности на квантовата теория на полето и космологията. Освен това, най-елегантните приложения на позитивната геометрия често включват суперсиметрични системи или плоски пространства-времена. Това са идеални условия, които може да не отразяват реалната структура на Вселената.
От решаващо значение е, че макар и математически убедителни, идеите, представени в последната статия на д-р Февола и д-р Сателбергер, са съвсем нови и трябва да бъдат тествани спрямо по-строги и реалистични модели, преди да могат да послужат като основа за истинско обединение.
В крайна сметка, с всяка смела стъпка в теоретичната физика, пътят от абстракцията до физическата релевантност може да бъде дълъг и труден. Въпреки това, потенциалът на позитивната геометрия да преодолее най-дълбоките разделения и да предложи път към единна "Теория на всичко" е достатъчен, за да предизвика вълнение.
Като предлага свеж, елегантен математически език, способен да описва както взаимодействията на частиците, така и космическата еволюция, той кани изследователите да преосмислят Вселената не като мозайка от несвързани теории, а като единно геометрично цяло.
С развитието на областта, следващото предизвикателство се състои в превръщането на нейните абстрактни структури във физическа реалност – по едно уравнение и по един модел.
"Физиката предлага нови, интригуващи математически структури. Сега е оставено на общността да се заеме с детайлите на нововъзникващите математически обекти и теории и да ги удостовери", заключават изследователите. "Както е потвърдено от различни плодотворни и успешни сътрудничества, вече са направени важни първи стъпки."
Справка: Claudia Fevola et al, Algebraic and Positive Geometry of the Universe: From Particles to Galaxies, Notices of the American Mathematical Society (2025). DOI: 10.1090/noti3220. www.ams.org/journals/notices/2 … .html?adat=September
Източник: Could Mysterious New Shapes and ‘Positive Geometry’ Help Researchers Discover a “Theory of Everything”?, Tim McMillan, The Debrief
Още по темата
Физика
Примиряване на непримиримите - гравитацията и другите фундаментални сили?
Физика
Защо виртуалните частици не съществуват, но обясняват реалността - засега
Физика
Физици пренаписват квантово правило, което противоречи на нашата Вселена
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Доколко съвместими са минерално-суровинният отрасъл и чистата околна среда?
Козон
Мистериозен череп на гръцки хоминин е датиран на поне 286 000 години
Peter Petrov
След многократни експлозии нов тест за мегаракетата на Мъск
поп Дръвчо
Гледайте за първи път на живо как новооткритият "междузвезден посетител" 3I/ATLAS се устремява към нас