

"–Ґ–Њ–≤–∞ –µ –љ–µ–Њ—З–∞–Ї–≤–∞–љ–Њ, –Є–Ј–љ–µ–љ–∞–і–≤–∞—Й–Њ - –Є –Ј–∞ –Љ–µ–љ –љ–µ–≤–µ—А–Њ—П—В–љ–Њ –≤—К–ї–љ—Г–≤–∞—Й–Њ. –Ч–∞ –і–∞ –±—К–і–∞ —З–µ—Б—В–µ–љ, –љ–∞ –љ—П–Ї–∞–Ї–≤–Њ –љ–Є–≤–Њ —А–∞–±–Њ—В—П –Ј–∞ —В–Њ–≤–∞ –±–ї–Є–Ј–Њ 50 –≥–Њ–і–Є–љ–Є. –Э–Њ –µ–і–≤–∞ –≤ –њ–Њ—Б–ї–µ–і–љ–Є—В–µ –љ—П–Ї–Њ–ї–Ї–Њ –Љ–µ—Б–µ—Ж–∞ –љ–∞–є-–љ–∞–Ї—А–∞—П —Б–µ –Њ–±–µ–і–Є–љ–Є—Е–∞. –Ш –µ –Љ–љ–Њ–≥–Њ –њ–Њ-–њ—А–µ–Ї—А–∞—Б–љ–Њ –Є –Ї—А–∞—Б–Є–≤–Њ, –Њ—В–Ї–Њ–ї–Ї–Њ—В–Њ –љ—П–Ї–Њ–≥–∞ —Б—К–Љ —Б–Є –њ—А–µ–і—Б—В–∞–≤—П–ї".
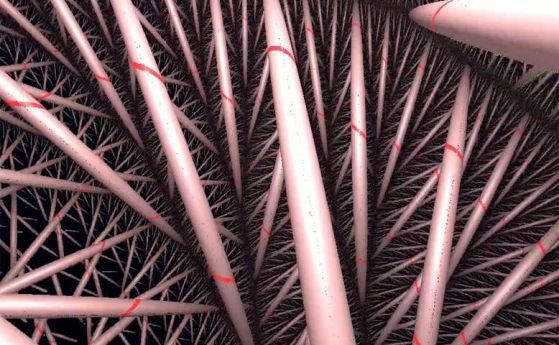
–Ґ–∞–Ї–∞ –Ј–∞–њ–Њ—З–≤–∞ –Є–Ј–ї–Њ–ґ–µ–љ–Є–µ—В–Њ —Б–Є —Д–Є–Ј–Є–Ї—К—В –Є –Ї–Њ–Љ–њ—О—В—К—А–µ–љ —Г—З–µ–љ –°—В–Є–≤—К–љ –Т–Њ–ї—Д—А–∞–Љ (Stephen Wolfram). –Ґ–Њ–є —Б–Љ—П—В–∞, —З–µ –Т—Б–µ–ї–µ–љ–∞—В–∞ –µ –Њ–≥—А–Њ–Љ–љ–∞, –љ–∞—А–∞—Б—В–≤–∞—Й–∞ –Љ—А–µ–ґ–∞ –Њ—В –≤–Ј–∞–Є–Љ–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П, –Ї–Њ–Є—В–Њ —Б—К—Б—В–∞–≤–ї—П–≤–∞—В —Б–∞–Љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Є –≤—Б–Є—З–Ї–Њ –≤ –љ–µ–≥–Њ. –Т —В–∞–Ј–Є –Ї–∞—А—В–Є–љ–∞ –Т–Њ–ї—Д—А–∞–Љ –≤–Є–ґ–і–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –µ–і–љ–∞ –Њ–Ї–Њ–љ—З–∞—В–µ–ї–љ–∞ —В–µ–Њ—А–Є—П, –Ї–Њ—П—В–Њ –ї–µ–ґ–Є –≤ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –≤—Б–Є—З–Ї–Є —Д–Є–Ј–Є—З–љ–Є –Ј–∞–Ї–Њ–љ–Є.
–Ш–Ј—Г—З–∞–≤–∞–є–Ї–Є "–Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞ –љ–∞ –њ—А–Њ—Б—В–Є –њ—А–Њ–≥—А–∞–Љ–Є" –≤ –љ–∞—З–∞–ї–Њ—В–Њ –љ–∞ 80-—В–µ, —В–Њ–є –њ—А–∞–≤–Є –Ј–∞ —Б–µ–±–µ —Б–Є –µ–і–љ–Њ –Љ–љ–Њ–≥–Њ –Є–Ј–љ–µ–љ–∞–і–≤–∞—Й–Њ –Є –≤–∞–ґ–љ–Њ –Њ—В–Ї—А–Є—В–Є–µ: —З–µ –і–Њ—А–Є –Ї–Њ–≥–∞—В–Њ –Њ—Б–љ–Њ–≤–љ–Є—В–µ –њ—А–∞–≤–Є–ї–∞ –Ј–∞ –µ–і–љ–∞ —Б–Є—Б—В–µ–Љ–∞ —Б–∞ –Є–Ј–Ї–ї—О—З–Є—В–µ–ї–љ–Њ –њ—А–Њ—Б—В–Є, –њ–Њ–≤–µ–і–µ–љ–Є–µ—В–Њ –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ –Ї–∞—В–Њ —Ж—П–ї–Њ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –њ–Њ —Б—К—Й–µ—Б—В–≤–Њ –њ—А–Њ–Є–Ј–≤–Њ–ї–љ–Њ –±–Њ–≥–∞—В–Њ –Є —Б–ї–Њ–ґ–љ–Њ.
"–Ш —В–Њ–≤–∞ –Љ–µ –љ–∞–Ї–∞—А–∞ –і–∞ —Б–µ –Ј–∞–Љ–Є—Б–ї—П: –Ь–Њ–ґ–µ –ї–Є –Т—Б–µ–ї–µ–љ–∞—В–∞ –і–∞ —А–∞–±–Њ—В–Є –њ–Њ —В–Њ–Ј–Є –љ–∞—З–Є–љ? –Т—К–Ј–Љ–Њ–ґ–љ–Њ –ї–Є –µ –≤—Б—К—Й–љ–Њ—Б—В, —З–µ –њ–Њ–і —Ж—П–ї–Њ—В–Њ —В–Њ–≤–∞ –±–Њ–≥–∞—В—Б—В–≤–Њ –Є —Б–ї–Њ–ґ–љ–Њ—Б—В, –Ї–Њ–Є—В–Њ –≤–Є–ґ–і–∞–Љ–µ –≤—К–≤ —Д–Є–Ј–Є–Ї–∞—В–∞, –Є–Љ–∞ –њ—А–Њ—Б—В–Њ –њ—А–Њ—Б—В–Є –њ—А–∞–≤–Є–ї–∞?¬†"
–°–≤–Њ–Є—В–µ –Є–і–µ–Є –Њ—В–њ—А–µ–і–Є 18 –≥–Њ–і–Є–љ–Є –Т–Њ–ї—Д—А–∞–Љ –њ—А–µ–і—Б—В–∞–≤—П —В–Њ–≥–∞–≤–∞ –≤ —В–Њ–Љ –Њ—В 1197 —Б—В—А–∞–љ–Є—Ж–Є, –Њ–Ј–∞–≥–ї–∞–≤–µ–љвАЮ–Э–Њ–≤ –≤–Є–і –љ–∞—Г–Ї–∞вАЬ (A New Kind of Science). –Э–Њ –Њ–љ–Њ–≤–∞ –≤—А–µ–Љ–µ –Ї–∞—А—В–Є–љ–∞—В–∞ –Љ—Г –µ –≤—Б–µ –Њ—Й–µ –Љ–∞–ї–Ї–Њ —А–∞–Ј–Љ–Є—В–∞.
–°–µ–≥–∞ —В–Њ–є —Б–Љ—П—В–∞, —З–µ –µ –љ–∞–Љ–µ—А–Є–ї –њ–Њ-–Њ—В—З–µ—В–ї–Є–≤–∞ –≤–Є–Ј–Є—П –Ї–∞–Ї –Љ–Њ–ґ–µ –і–∞ —Б–µ –Њ–±—П—Б–љ–Є —А–µ–∞–ї–љ–Њ—Б—В—В–∞.
–Т –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –њ–Њ–і—Е–Њ–і–∞ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –µ –њ—А–µ–і—Б—В–∞–≤–∞—В–∞ –Ј–∞ —Е–Є–њ–µ—А–≥—А–∞—Д. вАЮ–У—А–∞—Д—К—ВвАЬ –≤ —В–Њ–Ј–Є –Ї–Њ–љ—В–µ–Ї—Б—В –µ –Ї–∞—В–Њ —Б—Е–µ–Љ–∞—В–Є—З–љ–Њ—В–Њ –њ—А–µ–і—Б—В–∞–≤—П–љ–µ –љ–∞ –Љ—А–µ–ґ–∞: –ї–Є–љ–Є–Є, —Б–≤—К—А–Ј–≤–∞—Й–Є —В–Њ—З–Ї–Є. –Э–Њ —А–µ–∞–ї–љ–Њ—Б—В—В–∞ –љ–µ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ —Г–ї–Њ–≤–µ–љ–∞ –Њ—В –ї–Є–љ–Є–Є, —Б–≤—К—А–Ј–≤–∞—Й–Є —В–Њ—З–Ї–Є –љ–∞ –њ–ї–Њ—Б—К–Ї –ї–Є—Б—В —Е–∞—А—В–Є—П.¬†–Т–Њ–ї—Д—А–∞–Љ –≥–µ–љ–µ—А–Є—А–∞ –Ї–Њ–Љ–њ—О—В—К—А–љ–Є –≤–Є–Ј—Г–∞–ї–Є–Ј–∞—Ж–Є–Є, –Ј–∞ –і–∞ –Є–Ј–Њ–±—А–∞–Ј–Є –≤–Ј–∞–Є–Љ–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П—В–∞ –≤ –њ–Њ-—Б–ї–Њ–ґ–љ–Є вАЮ—Е–Є–њ–µ—А–≥—А–∞—Д–ЄвАЬ. (–Т —Е–Є–њ–µ—А–≥—А–∞—Д–∞ вАЮ–ї–Є–љ–Є–Є—В–µвАЬ –Љ–Њ–≥–∞—В –і–∞ —Б–≤—К—А–Ј–≤–∞—В –њ—А–Њ–Є–Ј–≤–Њ–ї–µ–љ –±—А–Њ–є —В–Њ—З–Ї–Є, –∞ –љ–µ —Б–∞–Љ–Њ –і–≤–µ.)
–Ш–Ј—Б–ї–µ–і–≤–∞–љ–Є—П—В–∞ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –њ–Њ–Ї–∞–Ј–≤–∞—В, —З–µ —Б–ї–Њ–ґ–љ–Є—В–µ —Е–Є–њ–µ—А–≥—А–∞—Д–Є –Љ–Њ–≥–∞—В –і–∞ –Є–Љ–Є—В–Є—А–∞—В –Љ–љ–Њ–≥–Њ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞, –≤–Ї–ї—О—З–Є—В–µ–ї–љ–Њ –Љ–∞—В–µ—А–Є—П –Є –µ–љ–µ—А–≥–Є—П, –∞ —Б—К—Й–Њ –Є –і–∞ –≤—К–Ј–њ—А–Њ–Є–Ј–≤–µ–і–∞—В —Д–Є–Ј–Є—З–љ–Є—В–µ —Б—В—А—Г–Ї—В—Г—А–Є –Є –њ—А–Њ—Ж–µ—Б–Є, –Њ–њ–Є—Б–∞–љ–Є –Њ—В —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ –Є –Ї–≤–∞–љ—В–Њ–≤–∞—В–∞ –Љ–µ—Е–∞–љ–Є–Ї–∞.
–Ш –Љ–∞–Ї–∞—А —В–Њ–≤–∞ –і–∞ —Б–∞¬†–Ї–∞–Љ–∞—А–∞ –љ–Њ–≤–Є –Є–і–µ–Є, –Љ–Њ–і–µ–ї–Є—В–µ –Є–Љ–∞—В —А–∞–Ј–ї–Є—З–љ–∞ –±–∞–Ј–Њ–≤–∞¬†—Б—В—А—Г–Ї—В—Г—А–∞, –Ї–∞–Ї—В–Њ –Є –Љ–µ—В–Њ–і–Є—В–µ —Б–∞ —А–∞–Ј–ї–Є—З–љ–Є, —В—Г–Ї –љ–µ —Б—В–∞–≤–∞ –≤—К–њ—А–Њ—Б вАЮ–і–∞ –Є–Ј—Е–≤—К—А–ї–Є¬†—Б—В–∞—А–∞—В–∞ —Д–Є–Ј–Є–Ї–∞вАЬ. –Т–Њ–ї—Д—А–∞–Љ –Ї–∞–Ј–≤–∞, —З–µ "–Ј–∞ –і–∞ —А–∞–±–Њ—В–Є –≤—Б–Є—З–Ї–Њ, —Й–µ —В—А—П–±–≤–∞ –і–∞ –љ–∞–і–≥—А–∞–ґ–і–∞–Љ–µ".
"–†–∞–і–≤–∞–Љ —Б–µ –і–∞ –Ї–∞–ґ–∞, —З–µ –Љ–Є—Б–ї—П, —З–µ —Б–Љ–µ –љ–∞–Љ–µ—А–Є–ї–Є –њ—К—В –Ї—К–Љ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї–љ–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞. –°—К–Ј–і–∞–і–Њ—Е–Љ–µ –њ–∞—А–∞–і–Є–≥–Љ–∞ –Є —А–∞–Љ–Ї–∞ (–Є, –і–∞, —Б—К—Й–Њ —Б–Љ–µ –Є–Ј–≥—А–∞–і–Є–ї–Є –Љ–љ–Њ–≥–Њ –і–Њ–±—А–Є, –њ—А–∞–Ї—В–Є—З–љ–Є –Є –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–Є –Є–љ—Б—В—А—Г–Љ–µ–љ—В–Є ). –Э–Њ —Б–µ–≥–∞ —В—А—П–±–≤–∞ –і–∞ –Ј–∞–≤—К—А—И–Є–Љ —А–∞–±–Њ—В–∞—В–∞. –Ґ—А—П–±–≤–∞ –і–∞ —А–∞–±–Њ—В–Є–Љ —Б –Љ–љ–Њ–≥–Њ —Б–ї–Њ–ґ–љ–Є –Є–Ј—З–Є—Б–ї–µ–љ–Є—П, –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –Є —Д–Є–Ј–Є–Ї–∞. –Ш¬†–і–∞ –≤–Є–і–Є–Љ –і–∞–ї–Є –љ–∞–є-–љ–∞–Ї—А–∞—П —Й–µ –Љ–Њ–ґ–µ–Љ –і–∞ –і–∞–і–µ–Љ –Њ—В–≥–Њ–≤–Њ—А–∞ –љ–∞ —В–Њ–≤–∞ –Ї–∞–Ї —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї–љ–Њ —А–∞–±–Њ—В–Є –љ–∞—И–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞", –њ—А–µ–і—Б—В–∞–≤—П –Т–Њ–ї—Д—А–∞–Љ —Б–≤–Њ–µ—В–Њ "–≥–Њ–ї—П–Љ–Њ –Є –Є—Б—В–Њ—А–Є—З–µ—Б–Ї–Њ –Є–љ—В–µ–ї–µ–Ї—В—Г–∞–ї–љ–Њ –њ—А–Є–Ї–ї—О—З–µ–љ–Є–µ" - —Б–≤–Њ—П¬†–њ—А–Њ–µ–Ї—В –њ–Њ —Д–Є–Ј–Є–Ї–∞.
–Ъ–∞–Ї —А–∞–±–Њ—В–Є
–Т—Б–Є—З–Ї–Њ –Ј–∞–њ–Њ—З–≤–∞ —Б –љ–µ—Й–Њ –Љ–љ–Њ–≥–Њ –њ—А–Њ—Б—В–Њ –Є –Љ–љ–Њ–≥–Њ –±–µ–Ј—Б—В—А—Г–Ї—В—Г—А–љ–Њ¬†- —Б—К–≤–Ї—Г–њ–љ–Њ—Б—В –Њ—В –∞–±—Б—В—А–∞–Ї—В–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –∞–±—Б—В—А–∞–Ї—В–љ–Є –µ–ї–µ–Љ–µ–љ—В–Є.¬†–Ґ–Њ–≤–∞ –µ —Б–њ–Њ–Љ–µ–љ–∞—В–Є—П—В –њ–Њ-—А–∞–љ–Њ¬†—Е–Є–њ–µ—А–≥—А–∞—Д - –Є–ї–Є, –≤ –њ—А–Њ—Б—В–Є—В–µ —Б–ї—Г—З–∞–Є,¬†–≥—А–∞—Д.
–Ф–∞ —А–µ—З–µ–Љ, —З–µ –Є–Љ–∞–Љ–µ –Ї–Њ–ї–µ–Ї—Ж–Є—П –Њ—В –Њ—В–љ–Њ—И–µ–љ–Є—П –Ї–∞—В–Њ:
{{1, 2}, {2, 3}, {3, 4}, {2, 4}}
–Ї–Њ–Є—В–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –њ—А–µ–і—Б—В–∞–≤–µ–љ–Є –Њ—В –≥—А–∞—Д¬†—В–∞–Ї–∞:
  
 
–Ґ–Њ–≤–∞ —Б–∞ –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –µ–ї–µ–Љ–µ–љ—В–Є (–Ї–∞—В–Њ {2,3} ). –†–µ–і—К—В, –≤ –Ї–Њ–є—В–Њ —Б–∞ –Ј–∞—П–≤–µ–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П—В–∞, –љ—П–Љ–∞ –Ј–љ–∞—З–µ–љ–Є–µ (–≤—К–њ—А–µ–Ї–Є —З–µ —А–µ–і—К—В –≤—К–≤ –≤—Б—П–Ї–∞ –≤—А—К–Ј–Ї–∞ –Є–Љ–∞ –Ј–љ–∞—З–µ–љ–Є–µ). –Ґ–Њ–≤–∞, –Ї–Њ–µ—В–Њ –Є–Љ–∞ –Ј–љ–∞—З–µ–љ–Є–µ, –µ –Ї–Њ–µ –µ —Б–≤—К—А–Ј–∞–љ–Њ —Б –Ї–Њ–µ. –Э—П–Љ–∞ –Ј–љ–∞—З–µ–љ–Є–µ –Ї–∞–Ї —Б–µ –љ–∞—А–Є—З–∞—В вАЛвАЛ–µ–ї–µ–Љ–µ–љ—В–Є—В–µ. –Ґ—Г–Ї —Б–∞ –Є–Ј–њ–Њ–ї–Ј–≤–∞–љ–Є —З–Є—Б–ї–∞, –љ–Њ –≤–∞–ґ–љ–Њ—В–Њ –µ,¬†–і–∞–ї–Є –µ–ї–µ–Љ–µ–љ—В–Є—В–µ —Б–∞ –µ–і–љ–∞–Ї–≤–Є –Є–ї–Є —А–∞–Ј–ї–Є—З–љ–Є.
–Ф–∞ –њ—А–Є–ї–Њ–ґ–Є–Љ –µ–і–љ–Њ –њ—А–Њ—Б—В–Њ –њ—А–∞–≤–Є–ї–Њ –Ї—К–Љ —В—П—Е, –Њ—В–љ–Њ–≤–Њ –Є –Њ—В–љ–Њ–≤–Њ. –Х—В–Њ –њ—А–Є–Љ–µ—А –Ј–∞ –≤—К–Ј–Љ–Њ–ґ–љ–Њ –њ—А–∞–≤–Є–ї–Њ:
{{
–Ъ–∞–Ї —Б—В–∞–≤–∞ –њ—А–Є–ї–∞–≥–∞–љ–µ—В–Њ –љ–∞ —В–Њ–≤–∞ –њ—А–∞–≤–Є–ї–Њ?
–Т–Ј–µ–Љ–∞—В–µ –і–≤–µ –Њ—В–љ–Њ—И–µ–љ–Є—П - –Њ—В –≤—Б—П–Ї–∞ —В–Њ—З–Ї–∞ –љ–∞ –Ї–Њ–ї–µ–Ї—Ж–Є—П—В–∞ - –Є –≤–Є–ґ–і–∞—В–µ –і–∞–ї–Є –µ–ї–µ–Љ–µ–љ—В–Є—В–µ –≤ —В—П—Е —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞—В –љ–∞ –Љ–Њ–і–µ–ї–∞ {{
–Ь–Њ–ґ–µ–Љ –і–∞ –њ—А–µ–і—Б—В–∞–≤–Є–Љ –њ—А–∞–≤–Є–ї–Њ—В–Њ –Ї–∞—В–Њ –њ—А–µ–Њ–±—А–∞–Ј—Г–≤–∞–љ–µ –љ–∞ –≥—А–∞—Д–Є–Ї–Є:

–°–µ–≥–∞ –љ–µ–Ї–∞ –њ—А–Є–ї–Њ–ґ–Є–Љ –њ—А–∞–≤–Є–ї–Њ—В–Њ –≤–µ–і–љ—К–ґ –Ї—К–Љ:
{{1, 2}, {2, 3}, {3, 4}, {2, 4}}
–Ю—В–љ–Њ—И–µ–љ–Є—П—В–∞ {2,3} –Є {2,4} —Б—К–≤–њ–∞–і–∞—В –Є –њ—А–∞–≤–Є–ї–Њ—В–Њ –≥–Є –Ј–∞–Љ–µ—Б—В–≤–∞ —Б —З–µ—В–Є—А–Є –љ–Њ–≤–Є –Њ—В–љ–Њ—И–µ–љ–Є—П, —В–∞–Ї–∞ —З–µ —А–µ–Ј—Г–ї—В–∞—В—К—В –µ:
{{1, 2}, {3, 4}, {2, 4}, {2, 5}, {3, 5}, {4, 5}}
–Ь–Њ–ґ–µ–Љ –і–∞ –њ—А–µ–і—Б—В–∞–≤–Є–Љ —В–Њ–Ј–Є —А–µ–Ј—Г–ї—В–∞—В –Ї–∞—В–Њ –≥—А–∞—Д (–Ї–Њ–є—В–Њ —Б–µ –Њ–Ї–∞–Ј–≤–∞ –Њ–±—К—А–љ–∞—В —Б–њ—А—П–Љ–Њ –≥—А–∞—Д–∞ –њ–Њ-–≥–Њ—А–µ):

–Х—В–Њ —А–µ–Ј—Г–ї—В–∞—В–∞, –∞–Ї–Њ –њ—А–Њ—Б—В–Њ –њ—А–Њ–і—К–ї–ґ–Є–Љ –і–∞ –њ—А–Є–ї–∞–≥–∞–Љ–µ –њ—А–∞–≤–Є–ї–Њ—В–Њ –Њ—В–љ–Њ–≤–Њ –Є –Њ—В–љ–Њ–≤–Њ:

–Ю—Й–µ –љ—П–Ї–Њ–ї–Ї–Њ –њ—К—В–Є –Є –µ—В–Њ –µ–і–љ–∞ –њ–Њ-–≥–Њ–ї—П–Љ–∞ –Ї–∞—А—В–Є–љ–∞:

–Ъ–∞–Ї–≤–Њ —Б—В–∞–≤–∞ —В—Г–Ї? –Ш–Љ–∞–Љ–µ —В–Њ–ї–Ї–Њ–≤–∞ –њ—А–Њ—Б—В–Њ –њ—А–∞–≤–Є–ї–Њ. –Э–Њ –њ—А–Є–ї–∞–≥–∞–љ–µ—В–Њ –љ–∞ —В–Њ–≤–∞ –њ—А–∞–≤–Є–ї–Њ –Њ—В–љ–Њ–≤–Њ –Є –Њ—В–љ–Њ–≤–Њ –њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –Є–Ј–≥–ї–µ–ґ–і–∞ –љ–∞–Є—Б—В–Є–љ–∞ —Б–ї–Њ–ґ–љ–Њ. –Ш –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–∞—В–∞ –љ–Є –Є–љ—В—Г–Є—Ж–Є—П –љ–µ –Љ–Њ–ґ–µ –і–∞ –њ—А–µ–і—Б–Ї–∞–ґ–µ, —З–µ —Й–µ —Б–µ —Б–ї—Г—З–Є.¬†
–Р–Ї–Њ –њ—А–µ–љ–µ–±—А–µ–≥–љ–µ–Љ —Ж—П–ї–∞—В–∞ –Љ–∞—В–µ—А–Є—П –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞, –љ–∞—И–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞ –µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Є —В–Њ –Љ–љ–Њ–≥–Њ –њ—А–Є–ї–Є—З–∞ –љ–∞ –Ї–∞—А—В–Є–љ–Ї–∞—В–∞ –њ–Њ-–≥–Њ—А–µ, —Б–њ–Њ—А–µ–і –Т–Њ–ї—Д—А–∞–Љ. –°—К–≤–Ї—Г–њ–љ–Њ—Б—В –Њ—В –њ–Њ —Б—К—Й–µ—Б—В–≤–Њ –∞–±—Б—В—А–∞–Ї—В–љ–Є —В–Њ—З–Ї–Є, –∞–±—Б—В—А–∞–Ї—В–љ–Њ —Б–≤—К—А–Ј–∞–љ–Є –њ–Њ–Љ–µ–ґ–і—Г —Б–Є. –°–∞–Љ–Њ —З–µ –љ–∞ —Б–љ–Є–Љ–Ї–∞—В–∞ –Є–Љ–∞ 6704 –Њ—В —В–µ–Ј–Є —В–Њ—З–Ї–Є, –і–Њ–Ї–∞—В–Њ –≤ –љ–∞—И–∞—В–∞ —А–µ–∞–ї–љ–∞ –≤—Б–µ–ї–µ–љ–∞ –Љ–Њ–ґ–µ –і–∞ –Є–Љ–∞ –њ–Њ–≤–µ—З–µ –Њ—В 10400¬†–Є–ї–Є –і–Њ—А–Є –Љ–љ–Њ–≥–Њ –њ–Њ–≤–µ—З–µ.
–Т—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—А–∞–≤–Є–ї–∞
–Ъ–Њ–µ –њ—А–∞–≤–Є–ї–Њ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –љ–∞—И–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞? –Э–µ –µ –љ–∞–Љ–µ—А–µ–љ–Њ –Њ—Й–µ –Є —Б–Є–≥—Г—А–љ–Њ –љ–µ –µ –Њ–њ–Є—Б–∞–љ–Њ—В–Њ –њ–Њ-–≥–Њ—А–µ. –Ґ—Г–Ї –Т–Њ–ї—Д—А–∞–Љ –Њ–±—Б—К–ґ–і–∞¬†–Ї–∞–Ї–≤–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—А–∞–≤–Є–ї–∞ –Є–Љ–∞ –Є –Ї–∞–Ї–≤–Њ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ –њ—А–∞–≤—П—В.
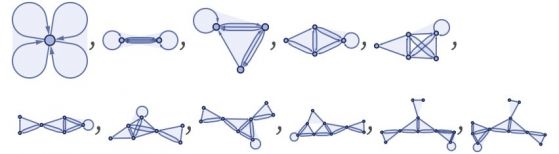
–Х–і–љ–∞ –Њ—Б–Њ–±–µ–љ–Њ—Б—В –љ–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ, –Ї–Њ–µ—В–Њ –±–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞–љ–Њ –њ–Њ-–≥–Њ—А–µ, –µ, —З–µ —В–Њ —Б–µ –Њ—Б–љ–Њ–≤–∞–≤–∞ –љ–∞ –Ї–Њ–ї–µ–Ї—Ж–Є–Є –Њ—В вАЮ–±–Є–љ–∞—А–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—ПвАЬ, —Б—К–і—К—А–ґ–∞—Й–Є –і–≤–Њ–є–Ї–Є –µ–ї–µ–Љ–µ–љ—В–Є (–љ–∞–њ—А–Є–Љ–µ—А {2,3}). –Э–Њ —Б—К—Й–∞—В–∞ —Б—Е–µ–Љ–∞ –њ–Њ–Ј–≤–Њ–ї—П–≤–∞ –і–∞ —Б–µ —А–∞–Ј–≥–ї–µ–і–∞—В –Њ—В–љ–Њ—И–µ–љ–Є—П—В–∞ –Є —Б –њ–Њ–≤–µ—З–µ –µ–ї–µ–Љ–µ–љ—В–Є. –Э–∞–њ—А–Є–Љ–µ—А, –µ—В–Њ –Ї–Њ–ї–µ–Ї—Ж–Є—П –Њ—В –і–≤–µ —В—А–Њ–є–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П:
{{1, 2, 3}, {3, 4, 5}}
–Э–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ –≥—А–∞—Д, –љ–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞¬†—Е–Є–њ–µ—А–≥—А–∞—Д - –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є—П, –њ—А–Є –Ї–Њ—П—В–Њ —Б–µ –Њ–±–Њ–±—Й–∞–≤–∞—В —А—К–±–Њ–≤–µ—В–µ –≤ –≥—А–∞—Д–Є, –Ї–Њ–Є—В–Њ —Б–≤—К—А–Ј–≤–∞—В –і–≤–Њ–є–Ї–Є –≤—К–Ј–ї–Є —Б вАЮ—Е–Є–њ–µ—А–≤—К–Ј–ї–ЄвАЬ, –Ї–Њ–Є—В–Њ —Б–≤—К—А–Ј–≤–∞—В –њ—А–Њ–Є–Ј–≤–Њ–ї–µ–љ –±—А–Њ–є –≤—К–Ј–ї–Є:

(–•–Є–њ–µ—А–≥—А–∞—Д–Є—В–µ —Б–∞ –љ–∞—Б–Њ—З–µ–љ–Є, –Ї—К–і–µ—В–Њ –Є–Љ–∞ –Ј–љ–∞—З–µ–љ–Є–µ —А–µ–і—К—В, –≤ –Ї–Њ–є—В–Њ –≤—К–Ј–ї–Є—В–µ —Б–µ –њ–Њ—П–≤—П–≤–∞—В –≤ —Е–Є–њ–µ—А–≤—К–Ј–µ–ї–∞. –Э–∞ –Є–ї—О—Б—В—А–∞—Ж–Є—П—В–∞ вАЮ–Љ–µ–Љ–±—А–∞–љ–Є—В–µвАЬ —Б–∞–Љ–Њ —Г–Ї–∞–Ј–≤–∞—В –Ї–Њ–Є –≤—К–Ј–ї–Є —Б–∞ —Б–≤—К—А–Ј–∞–љ–Є –Ї—К–Љ –µ–і–Є–љ –Є —Б—К—Й —Е–Є–њ–µ—А–≤—К–Ј–µ–ї.)
–Ь–Њ–ґ–µ –і–∞ —Б–µ –њ—А–Є–ї–Њ–ґ–∞—В –њ—А–∞–≤–Є–ї–∞ –Є –Ј–∞ —Е–Є–њ–µ—А–≥—А–∞—Д–Є:
{{

–Р–Ї–Њ —Б—В–∞—А—В–Є—А–∞–Љ–µ —В–Њ–≤–∞ –њ—А–∞–≤–Є–ї–Њ, –Ї–∞—В–Њ —Б–µ –Ј–∞–њ–Њ—З–љ–µ –Њ—В –љ–∞–є-–њ—А–Њ—Б—В–Є—П –≤—К–Ј–Љ–Њ–ґ–µ–љ —В—А–Њ–µ–љ —Е–Є–њ–µ—А–≥—А–∞—Д, —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ —В—А–Њ–µ–љ —Б–∞–Љ–Њ–Ј–∞—В–≤–∞—А—П—Й —Б–µ —Ж–Є–Ї—К–ї {{0,0,0}}:

–Р –µ—В–Њ –Ї–∞–Ї–≤–Њ —Б–µ —Б–ї—Г—З–≤–∞, –∞–Ї–Њ —Б–µ –Є–Ј–±–Є—А–∞—В –њ—А–Њ—Б—В–Є—З–Ї–Є –њ—А–∞–≤–Є–ї–∞ –љ–∞ —Б–ї—Г—З–∞–µ–љ –њ—А–Є–љ—Ж–Є–њ:

–Я–Њ –љ—П–Ї–∞–Ї—К–≤ –љ–∞—З–Є–љ —В–Њ–≤–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ –Љ–љ–Њ–≥–Њ –±–Є–Њ–ї–Њ–≥–Є—З–љ–Њ. –Э–Њ –≤—Б—К—Й–љ–Њ—Б—В —В–Њ–≤–∞ –і–µ–Љ–Њ–љ—Б—В—А–Є—А–∞, —З–µ –Є–Љ–∞ —А–∞–Ј–ї–Є—З–љ–Є –Њ–±—Й–Є —Д–Њ—А–Љ–Є –љ–∞ –њ–Њ–≤–µ–і–µ–љ–Є–µ, –љ—П–Ї–Њ–Є –њ—А–Њ—Б—В–Є, –∞ –і—А—Г–≥–Є –љ–µ.
–Х—В–Њ –Њ—Й–µ –љ—П–Ї–Њ–ї–Ї–Њ –њ—А–Є–Љ–µ—А–∞:

–Э–Њ –Љ–Њ–ґ–µ –ї–Є –Њ—В —В–∞–Ј–Є –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞ –≤—Б–µ–ї–µ–љ–∞ –Њ—В –њ—А–Њ—Б—В–Є –њ—А–∞–≤–Є–ї–∞ –і–∞ –љ–∞–Љ–µ—А–Є–Љ –љ–∞—И–∞—В–∞ —Д–Є–Ј–Є—З–µ—Б–Ї–∞ –≤—Б–µ–ї–µ–љ–∞?
–Ґ–Њ–≤–∞, –Ї–Њ–µ—В–Њ –≤–Є–ґ–і–∞–Љ–µ —В—Г–Ї, —Б–∞ —А–µ–Ј—Г–ї—В–∞—В–Є—В–µ –Њ—В –њ—А–Є–ї–∞–≥–∞–љ–µ—В–Њ –љ–∞ –њ—А–∞–≤–Є–ї–∞ –љ—П–Ї–Њ–ї–Ї–Њ —Е–Є–ї—П–і–Є –њ—К—В–Є¬†- –≤ –љ–∞—И–∞—В–∞ —А–µ–∞–ї–љ–∞ –≤—Б–µ–ї–µ–љ–∞ –Љ–Њ–ґ–µ –і–∞ —Б–∞ –љ—Г–ґ–љ–Є 10500¬†¬†–Є–ї–Є –і–Њ—А–Є –њ–Њ–≤–µ—З–µ.¬†
–Ґ–∞–Ј–Є –њ—А–Њ–њ–∞—Б—В –µ —В—А—Г–і–љ–Њ –њ—А–µ–Њ–і–Њ–ї–Є–Љ–∞. –°–њ–Њ—А–µ–і –Т–Њ–ї—Д—А–∞–Љ —В—А—П–±–≤–∞ –і–∞ —Б–µ —А–∞–±–Њ—В–Є –Њ—В –і–≤–µ –њ–Њ—Б–Њ–Ї–Є:
–Я—К—А–≤–Њ, —В—А—П–±–≤–∞ –і–∞ –Є–Ј–њ–Њ–ї–Ј–≤–∞–Љ–µ –љ–∞–є-–і–Њ–±—А–Њ—В–Њ –Њ–±–Њ–±—Й–µ–љ–Є–µ –љ–∞ —А–∞–±–Њ—В–∞—В–∞ –љ–∞ –љ–∞—И–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞, –Ї–Њ–µ—В–Њ —Б–Љ–µ –љ–∞—Г—З–Є–ї–Є –≤—К–≤ —Д–Є–Ј–Є–Ї–∞—В–∞ –њ—А–µ–Ј –њ–Њ—Б–ї–µ–і–љ–Є—В–µ –љ—П–Ї–Њ–ї–Ї–Њ –≤–µ–Ї–∞. –Ш –≤—В–Њ—А–Њ, —В—А—П–±–≤–∞ –і–∞ —Б—В–Є–≥–љ–µ–Љ –і–Њ—В–∞–Љ, –і–Њ–Ї–Њ–ї–Ї–Њ—В–Њ –Љ–Њ–ґ–µ–Љ, –Ј–∞ –і–∞ —А–∞–Ј–±–µ—А–µ–Љ –Ї–∞–Ї–≤–Њ –≤—Б—К—Й–љ–Њ—Б—В –њ—А–∞–≤—П—В –љ–∞—И–Є—В–µ –њ—А–∞–≤–Є–ї–∞.
–Ш —В—Г–Ї –Є–Љ–∞¬†–µ–і–Є–љ –±–∞–Ј–Њ–≤ –њ—А–Њ–±–ї–µ–Љ: —Д–µ–љ–Њ–Љ–µ–љ—К—В –љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ –љ–µ–њ—А–Є–≤–Њ–і–Є–Љ–Њ—Б—В. –Х–і–љ–Њ –Њ—В –≥–Њ–ї–µ–Љ–Є—В–µ –њ–Њ—Б—В–Є–ґ–µ–љ–Є—П –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—В–µ –љ–∞—Г–Ї–Є –µ –њ—А–µ–і–Њ—Б—В–∞–≤—П–љ–µ—В–Њ –љ–∞ —Г—А–∞–≤–љ–µ–љ–Є—П –Є —Д–Њ—А–Љ—Г–ї–Є, –Ї–Њ–Є—В–Њ –њ–Њ —Б—К—Й–µ—Б—В–≤–Њ –њ—А–µ–і—Б–Ї–∞–Ј–≤–∞—В –Ї–∞–Ї —Й–µ —Б–µ –і—К—А–ґ–Є –µ–і–љ–∞ —Б–Є—Б—В–µ–Љ–∞, –±–µ–Ј –і–∞ —Б–µ –љ–∞–ї–∞–≥–∞ –і–∞ —Б–µ –њ—А–Њ—Б–ї–µ–і—П–≤–∞ –≤—Б—П–Ї–∞ –љ–µ–є–љ–∞ —Б—В—К–њ–Ї–∞ –љ—К –і–µ–є—Б—В–≤–Є—П—В–∞ –є.
–Э–Њ –њ—А–µ–і–Є –Љ–љ–Њ–≥–Њ –≥–Њ–і–Є–љ–Є¬†–Т–Њ–ї—Д—А–∞–Љ —А–∞–Ј–±–Є—А–∞, —З–µ –≤ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞ –Њ—В –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—А–∞–≤–Є–ї–∞ —В–Њ–≤–∞ –Љ–љ–Њ–≥–Њ —З–µ—Б—В–Њ –µ –љ–µ–≤—К–Ј–Љ–Њ–ґ–љ–Њ. –Т–Љ–µ—Б—В–Њ —В–Њ–≤–∞, –і–Њ—А–Є –Є –і–∞ –µ –Є–Ј–≤–µ—Б—В–љ–Њ —В–Њ—З–љ–Њ—В–Њ –њ—А–∞–≤–Є–ї–Њ, –Ї–Њ–µ—В–Њ —Б–ї–µ–і–≤–∞ –µ–і–љ–∞ —Б–Є—Б—В–µ–Љ–∞, –Љ–Њ–ґ–µ –≤—Б–µ –њ–∞–Ї –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ —А–∞–Ј–±–µ—А–µ –Ї–∞–Ї–≤–Њ —Й–µ –љ–∞–њ—А–∞–≤–Є —Б–Є—Б—В–µ–Љ–∞—В–∞, –Њ—Б–≤–µ–љ –∞–Ї–Њ –љ–µ —Б–µ –њ—А–Њ—Б–ї–µ–і–Є –≤—Б—П–Ї–∞ –љ–µ–є–љ–∞ —Б—В—К–њ–Ї–∞.
–Э—П–Ї–Њ–є –Љ–Њ–ґ–µ –і–∞ –Ї–∞–ґ–µ, —З–µ —Б–ї–µ–і –Ї–∞—В–Њ –Ј–љ–∞–µ–Љ –њ—А–∞–≤–Є–ї–Њ—В–Њ –Ј–∞ –љ—П–Ї–∞–Ї–≤–∞ —Б–Є—Б—В–µ–Љ–∞, –љ–µ –±–Є —В—А—П–±–≤–∞–ї–Њ –і–∞ –Є–Љ–∞ –њ—А–Њ–±–ї–µ–Љ —Б –≤—Б–Є—З–Ї–Є—В–µ –љ–Є –Ї–Њ–Љ–њ—О—В—А–Є –Є –Є–љ—В–µ–ї–µ–Ї—В –≤–Є–љ–∞–≥–Є –і–∞ –Љ–Њ–ґ–µ–Љ –і–∞ –њ—А–µ–і–≤–Є–і–Є–Љ –Ї–∞–Ї–≤–Њ –±–Є –љ–∞–њ—А–∞–≤–Є–ї–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞. –Э–Њ –≤—Б—К—Й–љ–Њ—Б—В –Є–Љ–∞ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –Т–Њ–ї—Д—А–∞–Љ –љ–∞—А–Є—З–∞¬†–Я—А–Є–љ—Ж–Є–њ –љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ –µ–Ї–≤–Є–≤–∞–ї–µ–љ—В–љ–Њ—Б—В, —Б–њ–Њ—А–µ–і –Ї–Њ–є—В–Њ –њ–Њ—З—В–Є –≤–Є–љ–∞–≥–Є, –Ї–Њ–≥–∞—В–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ—В–Њ –љ–∞ –і–∞–і–µ–љ–∞ —Б–Є—Б—В–µ–Љ–∞ –љ–µ –µ –Њ—З–µ–≤–Є–і–љ–Њ –њ—А–Њ—Б—В–Њ, –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–Њ –µ —В–Њ–ї–Ї–Њ–≤–∞ —Б–ї–Њ–ґ–љ–Њ, –Ї–∞–Ї—В–Њ –≤—Б–Є—З–Ї–Њ –Њ—Б—В–∞–љ–∞–ї–Њ. –Ґ–∞–Ї–∞ —З–µ –љ—П–Љ–∞ –і–∞ –Љ–Њ–ґ–µ–Љ –і–∞ –≥–Њ "–Є–Ј—З–Є—Б–ї–Є–Љ" - –Є –Ј–∞ –і–∞ —А–∞–Ј–±–µ—А–µ–Љ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –њ—А–∞–≤–Є, —Й–µ –µ –љ—Г–ґ–µ–љ –љ–µ—А–µ–і—Г—Ж–Є—А—Г–µ–Љ –Њ–±–µ–Љ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ —А–∞–±–Њ—В–∞.
–Ґ–Њ–≤–∞ –Ј–∞¬†–Љ–Њ–і–µ–ї –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞ –µ –њ–Њ—В–µ–љ—Ж–Є–∞–ї–љ–Њ –≥–Њ–ї—П–Љ –њ—А–Њ–±–ї–µ–Љ.
–Э–Њ¬†–Т–Њ–ї—Д—А–∞–Љ¬†–µ –Њ—В–Ї—А–Є–ї, —З–µ –≤–Є–љ–∞–≥–Є, –Ї–Њ–≥–∞—В–Њ –Є–Љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞ –љ–µ—А–µ–і—Г—Ж–Є—А—Г–µ–Љ–Њ—Б—В –≤ —Б–Є—Б—В–µ–Љ–∞—В–∞, –Є–Љ–∞ –Є –±–µ–Ј–Ї—А–∞–µ–љ –±—А–Њ–є –і–ґ–Њ–±–Њ–≤–µ –љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞ —А–µ–і—Г—Ж–Є—А—Г–µ–Љ–Њ—Б—В. –Ш –Љ–∞–Ї–∞—А –і–∞ –µ –љ–∞–њ—К–ї–љ–Њ –љ–µ—П—Б–љ–Њ –і–∞–ї–Є –≤ —В–Њ–Ј–Є —Б–ї—Г—З–∞–є —В–µ–Ј–Є –і–ґ–Њ–±–Њ–≤–µ —Й–µ —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞—В¬† –љ–∞ —В–Њ–≤–∞, –Ї–Њ–Є—В–Њ –Ј–љ–∞–µ–Љ –Њ—В —Д–Є–Ј–Є–Ї–∞—В–∞. –Ш –њ—А–Є—П—В–љ–∞—В–∞ –Є–Ј–љ–µ–љ–∞–і–∞ –µ, —З–µ –Є–Ј–≥–ї–µ–ґ–і–∞ –Љ–љ–Њ–≥–Њ –Њ—В —В—П—Е –≥–Њ –њ—А–∞–≤—П—В.
–Ъ–∞–Ї–≤–Њ –µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ?
–Э–µ–Ї–∞ —А–∞–Ј–≥–ї–µ–і–∞–Љ–µ –µ–і–љ–Њ –њ—А–Њ—Б—В–Њ –њ—А–∞–≤–Є–ї–Њ –Њ—В –±–µ–Ј–Ї—А–∞–є–љ–∞—В–∞ –Ї–Њ–ї–µ–Ї—Ж–Є—П –љ–∞ –Т–Њ–ї—Д—А–∞–Љ:
{{
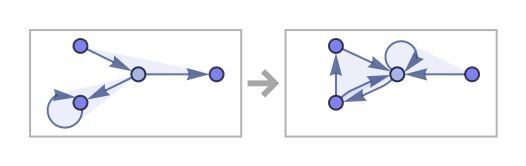
–Я–Њ –њ—К—А–≤–Є—В–µ 10 —Б—В—К–њ–Ї–Є –љ–µ –µ —П—Б–љ–Њ –Ї–∞–Ї–≤–Њ —Й–µ —Б–µ –њ–Њ–ї—Г—З–Є –љ–∞—В–∞—В—К–Ї:
–Э–Њ —Б–ї–µ–і 1000 —Б—В—К–њ–Ї–Є —Б—В–∞–≤–∞ —П—Б–љ–Њ: –њ—А–∞–≤–Є–ї–Њ—В–Њ —Б—К–Ј–і–∞–≤–∞ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–∞ –њ—А–Њ—Б—В–∞ —А–µ—И–µ—В–Ї–∞:
![]()
–Ш —Б–ї–µ–і –Є–Ј–≤–µ—Б—В–љ–Њ –≤—А–µ–Љ–µ —Б–µ —Б–ї—Г—З–≤–∞ —В–Њ–≤–∞:
–Я–Њ —Б—К—Й–µ—Б—В–≤–Њ —В–Њ–≤–∞ –љ–Є –њ—А–∞–≤–Є –Љ–љ–Њ–≥–Њ –њ—А–Њ—Б—В–Њ вАЮ–њ–∞—А—З–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–ЊвАЬ. –Р–Ї–Њ –њ—А–Њ–і—К–ї–ґ–Є–Љ –њ–Њ-–і—К–ї–≥–Њ –Є –њ–Њ-–і—К–ї–≥–Њ, —В–Њ–≤–∞ —Й–µ –љ–∞–њ—А–∞–≤–Є –њ–Њ-—Д–Є–љ–∞ –Є –њ–Њ-—Д–Є–љ–∞ –Љ—А–µ–ґ–∞, –і–Њ –Љ–Њ–Љ–µ–љ—В–∞, –≤ –Ї–Њ–є—В–Њ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –Є–Љ–∞–Љ–µ, –µ –њ–Њ—З—В–Є –љ–µ—А–∞–Ј–ї–Є—З–Є–Љ–Њ –Њ—В –њ–∞—А—З–µ –Њ—В –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–∞ —А–∞–≤–љ–Є–љ–∞.
–Х—В–Њ –і—А—Г–≥–Њ –њ—А–∞–≤–Є–ї–Њ:
{{ x, x, y }, { x, z,¬†u }} вЖТ {{ u, u, z }, { y, v,¬†z }, { y, v,¬†z }}
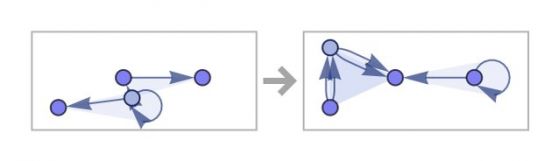
–Ъ–∞—В–Њ —А–∞–Ј–≥–ї–µ–і–∞–Љ–µ –њ—К—А–≤–Є—В–µ 10 —Б—В—К–њ–Ї–Є –љ–∞ –µ–≤–Њ–ї—О—Ж–Є—П—В–∞, –Њ—В–љ–Њ–≤–Њ –љ–µ –µ —П—Б–љ–Њ –Ї–∞–Ї–≤–Њ —Й–µ —Б–µ —Б–ї—Г—З–Є:
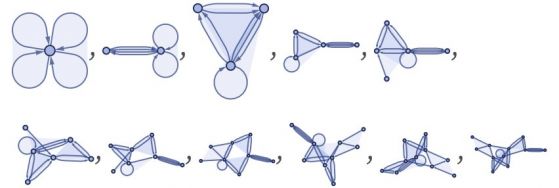
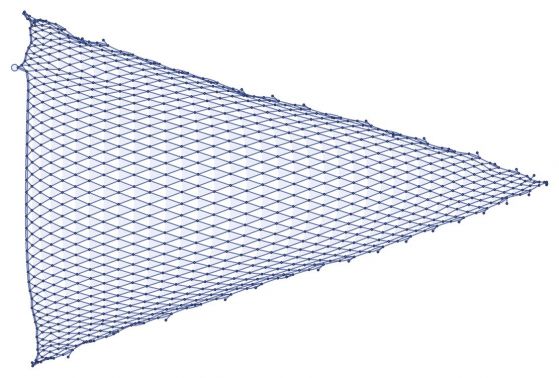
–Э–Њ —Б–ї–µ–і 1000 —Б—В—К–њ–Ї–Є —Б–µ –њ–Њ—П–≤–Є –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–∞ —Б—В—А—Г–Ї—В—Г—А–∞:
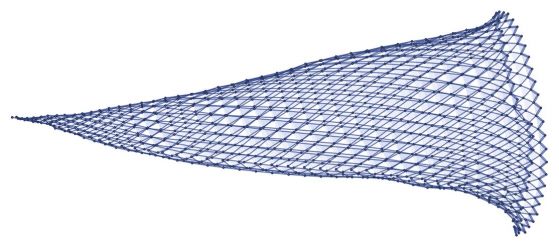
–Ш–Љ–∞ –і–∞–љ–љ–Є –Ј–∞ —А–µ—И–µ—В–Ї–∞, –љ–Њ —Б–µ–≥–∞ –≤–µ—З–µ –љ–µ –µ –њ–ї–Њ—Б–Ї–∞. –Т–Є–Ј—Г–∞–ї–Є–Ј–∞—Ж–Є—П—В–∞ –≤ 3D –њ—А–∞–≤–Є –њ–Њ-—П—Б–љ–Њ –Ї–∞–Ї–≤–Њ —Б–µ —Б–ї—Г—З–≤–∞: –Љ—А–µ–ґ–∞—В–∞ –µ—Д–µ–Ї—В–Є–≤–љ–Њ –Њ–њ—А–µ–і–µ–ї—П 2D –њ–Њ–≤—К—А—Е–љ–Њ—Б—В –≤ 3D:
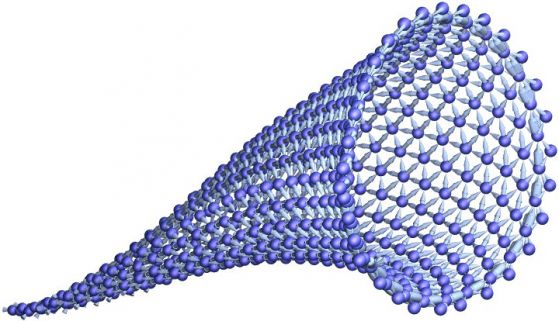
–Ф—А—Г–≥–Є –њ—А–∞–≤–Є–ї–∞ –њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞—В –і—А—Г–≥–Є —Д–Њ—А–Љ–Є. –Э–∞–њ—А–Є–Љ–µ—А, –њ—А–∞–≤–Є–ї–Њ—В–Њ:
{{
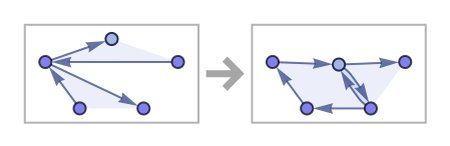
–і–∞–≤–∞ —Б–ї–µ–і 1000 —Б—В—К–њ–Ї–Є:

–†–µ–Ј—Г–ї—В–∞—В—К—В –љ–∞–Є—Б—В–Є–љ–∞ –µ —Б—В—А–∞–љ–µ–љ. –Ґ—А—К–≥–≤–∞ —Б–µ –Њ—В –њ—А–∞–≤–Є–ї–Њ, –Ї–Њ–µ—В–Њ –њ—А–Њ—Б—В–Њ —Г—В–Њ—З–љ—П–≤–∞ –Ї–∞–Ї –і–∞ —Б–µ –њ—А–µ–љ–∞–њ–Є—И–∞—В —З–∞—Б—В–Є –Њ—В –∞–±—Б—В—А–∞–Ї—В–µ–љ —Е–Є–њ–µ—А–≥—А–∞—Д –±–µ–Ј –љ–∞–Љ–µ–Ї –Ј–∞ –≥–µ–Њ–Љ–µ—В—А–Є—П –Є–ї–Є –љ–µ—Й–Њ –Ј–∞ 3D –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ. –Ш –≤—К–њ—А–µ–Ї–Є —В–Њ–≤–∞ —Б–µ —Б—В–Є–≥–∞ –і–Њ —Е–Є–њ–µ—А–≥—А–∞—Д, –Ї–Њ–є—В–Њ –њ—А–Є–ї–Є—З–∞ –љ–∞ 3D –њ–Њ–≤—К—А—Е–љ–Њ—Б—В.
–Т—К–њ—А–µ–Ї–Є —З–µ –µ–і–Є–љ—Б—В–≤–µ–љ–Њ—В–Њ –љ–∞–ї–Є—З–љ–Њ –љ–µ—Й–Њ —В—Г–Ї –µ –≤—А—К–Ј–Ї–∞—В–∞ –Љ–µ–ґ–і—Г —В–Њ—З–Ї–Є—В–µ, –Љ–Њ–ґ–µ–Љ –і–∞ вАЮ–Њ—В–≥–∞—В–љ–µ–ЉвАЬ –Ї—К–і–µ –Љ–Њ–ґ–µ –і–∞ –µ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞ –Є –µ—В–Њ —А–µ–Ј—Г–ї—В–∞—В—К—В –≤ 3D:

–Т—К–њ—А–µ–Ї–Є –≥–ї–∞–і–Ї–∞—В–∞ –Љ—Г —Д–Њ—А–Љ–∞, –Є–Ј–≥–ї–µ–ґ–і–∞, —З–µ –љ—П–Љ–∞ –њ—А–Њ—Б—В–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –љ–∞ —В–∞–Ј–Є –њ–Њ–≤—К—А—Е–љ–Њ—Б—В. (–Э–µ–≥–Њ–≤–∞—В–∞ —В—А–Є–њ–ї–∞—Б—В–Њ–≤–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ —В—П –љ–µ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–∞ –∞–ї–≥–µ–±—А–Є—З–љ–∞ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В¬†- —В—П –µ –њ–Њ–і–Њ–±–љ–∞, –љ–Њ –љ–µ –µ –Ї–∞—В–Њ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞
–Р–Ї–Њ –њ—А–Њ–і—К–ї–ґ–Є–Љ, —В–Њ–≥–∞–≤–∞ –Ї–∞—В–Њ –≤ –њ—А–Є–Љ–µ—А–∞ –љ–∞ —А–∞–≤–љ–Є–љ–∞—В–∞, –Љ—А–µ–ґ–∞—В–∞ —Й–µ —Б—В–∞–≤–∞ –њ–Њ-—Д–Є–љ–∞ –Є —Д–Є–љ–∞ —Б –љ–∞—А–∞—Б—В–≤–∞–љ–µ—В–Њ –љ–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ - —В–Њ—З–Ї–∞ –њ–Њ —В–Њ—З–Ї–∞, –≤—А—К–Ј–Ї–∞ —Б–ї–µ–і¬†–≤—А—К–Ј–Ї–∞ - –≤ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –µ –њ—А–Є–ї–Є—З–∞ –љ–∞ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–∞ 3D –њ–Њ–≤—К—А—Е–љ–Њ—Б—В, –Ї–Њ—П—В–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј—Г—З–∞–≤–∞ –≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—П –∞–љ–∞–ї–Є–Ј. –†–∞–Ј–±–Є—А–∞ —Б–µ, –≤ –љ—П–Ї–∞–Ї—К–≤ —Б–Љ–Є—Б—К–ї —В–Њ–≤–∞ –љ–µ –µ вАЮ–Є—Б—В–Є–љ—Б–Ї–∞вАЬ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В: —В–Њ–≤–∞ –µ –њ—А–Њ—Б—В–Њ —Е–Є–њ–µ—А–≥—А–∞—Д, –Ї–Њ–є—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞¬†–Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –∞–±—Б—В—А–∞–Ї—В–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П, –љ–Њ –њ–Њ –љ—П–Ї–∞–Ї—К–≤ –љ–∞—З–Є–љ –Љ–Њ–і–µ–ї—К—В –љ–∞ —В–µ–Ј–Є –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ—Г –њ—А–Є–і–∞–≤–∞ —Б—В—А—Г–Ї—В—Г—А–∞, –Ї–Њ—П—В–Њ –µ –њ–Њ-–±–ї–Є–Ј–Њ –Є –њ–Њ-–±–ї–Є–Ј–Њ –і–Њ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В.
–Ґ–∞–Ї–∞ –Љ–Є—Б–ї–Є –Т–Њ–ї—Д—А–∞–Љ, —З–µ —А–∞–±–Њ—В–Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞. –Ю—В–і–Њ–ї—Г —Б–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –і–Є—Б–Ї—А–µ—В–љ–Є, –∞–±—Б—В—А–∞–Ї—В–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –∞–±—Б—В—А–∞–Ї—В–љ–Є —В–Њ—З–Ї–Є. –Э–Њ –≤ –Љ–∞—Й–∞–±–∞, –≤ –Ї–Њ–є—В–Њ –ґ–Є–≤–µ–µ–Љ, –Љ–Њ–і–µ–ї—К—В –љ–∞ –Њ—В–љ–Њ—И–µ–љ–Є—П—В–∞, –≥–Њ –њ—А–∞–≤–Є –і–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Њ—В –≤–Є–і–∞, —Б –Ї–Њ–є—В–Њ —Б–Љ–µ —Б–≤–Є–Ї–љ–∞–ї–Є. –Ґ–Њ–≤–∞ –µ –Љ–∞–ї–Ї–Њ –Ї–∞—В–Њ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ —Б–µ —Б–ї—Г—З–≤–∞, –і–∞ —А–µ—З–µ–Љ, —Б –≤–Њ–і–∞—В–∞. –Ю—В–і–Њ–ї—Г –µ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –і–Є—Б–Ї—А–µ—В–љ–Є –Љ–Њ–ї–µ–Ї—Г–ї–Є, –љ–Њ –Ј–∞ –љ–∞—Б —В—П¬†–Є–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–∞ —В–µ—З–љ–Њ—Б—В.
–Ю—Й–µ –Њ—В –і—А–µ–≤–љ–Њ—Б—В—В–∞¬†—Е–Њ—А–∞—В–∞ —Б–∞ —Б–Љ—П—В–∞–ї–Є, —З–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –≤ –Ї—А–∞–є–љ–∞ —Б–Љ–µ—В–Ї–∞ –Љ–Њ–ґ–µ –і–∞¬† –і–Є—Б–Ї—А–µ—В–љ–Њ. –Э–Њ —Б—К–≤—А–µ–Љ–µ–љ–љ–∞—В–∞ —Д–Є–Ј–Є–Ї–∞ –љ–Є–Ї–Њ–≥–∞ –љ–µ –µ –Є–Љ–∞–ї–∞ –љ–∞—З–Є–љ –і–∞ –≥–Њ –њ—А–Њ–≤–µ—А–Є, –Њ—Б–≤–µ–љ —В–Њ–≤–∞ —В–∞–Ї–∞ –Є–ї–Є –Є–љ–∞—З–µ –µ –Љ–љ–Њ–≥–Њ –њ–Њ-—Г–і–Њ–±–љ–Њ¬†–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –і–∞ –±—К–і–µ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Њ, –Ј–∞ –і–∞ —Б–µ –Є–Ј—Б–ї–µ–і–≤–∞ –≤ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—П –∞–љ–∞–ї–Є–Ј. –Э–Њ —Б–µ–≥–∞ –Є–Ј–≥–ї–µ–ґ–і–∞, —З–µ –Є–і–µ—П—В–∞ –Ј–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –і–∞ –±—К–і–µ –і–Є—Б–Ї—А–µ—В–љ–Њ –≤—Б—К—Й–љ–Њ—Б—В –µ —А–µ—И–∞–≤–∞—Й–∞ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ—В–Њ –љ–∞ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї–љ–∞ —В–µ–Њ—А–Є—П –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞.
–†–∞–Ј–Љ–µ—А—К—В –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ
–Ь–љ–Њ–≥–Њ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї–µ–љ —Д–∞–Ї—В –Ј–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ, –≤ –Ї–Њ–µ—В–Њ –ґ–Є–≤–µ–µ–Љ, –µ, —З–µ —В–Њ –µ —В—А–Є–Є–Ј–Љ–µ—А–љ–Њ. –Ь–Њ–≥–∞—В –ї–Є –њ—А–∞–≤–Є–ї–∞—В–∞ –і–∞ –≤—К–Ј–њ—А–Њ–Є–Ј–≤–µ–і–∞—В —В–Њ–≤–∞?
–Ґ—А–Є¬†–Њ—В –њ–Њ—Б–ї–µ–і–љ–Є—В–µ –њ—А–∞–≤–Є–ї–∞ –њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞—В –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –ї–µ—Б–љ–Њ –Љ–Њ–ґ–µ–Љ –і–∞ —А–∞–Ј–њ–Њ–Ј–љ–∞–µ–Љ –Ї–∞—В–Њ –і–≤—Г–Є–Ј–Љ–µ—А–љ–Є –њ–Њ–≤—К—А—Е–љ–Њ—Б—В–Є - –≤ –µ–і–Є–љ–Є—П —Б–ї—Г—З–∞–є –њ–ї–Њ—Б–Ї–Є, –≤ –і—А—Г–≥–Є—В–µ¬†- –њ–Њ–і—А–µ–і–µ–љ–Є –≤ –Њ–њ—А–µ–і–µ–ї–µ–љ–∞ —Д–Њ—А–Љ–∞. –†–∞–Ј–±–Є—А–∞ —Б–µ, —В–Њ–≤–∞ —Б–∞ –Љ–љ–Њ–≥–Њ –љ–µ–њ—А–Є—П—В–љ–Є –њ—А–Є–Љ–µ—А–Є –Ј–∞ –і–≤—Г–Љ–µ—А–љ–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ: —В–µ –љ–∞ –њ—А–∞–Ї—В–Є–Ї–∞ —Б–∞ –њ—А–Њ—Б—В–Њ –њ—А–Њ—Б—В–Є —А–µ—И–µ—В–Ї–Є, –Љ–∞–Ї–∞—А —З–µ —В–Њ–≤–∞ –≥–Є –њ—А–∞–≤–Є –ї–µ—Б–љ–Є –Ј–∞ —А–∞–Ј–њ–Њ–Ј–љ–∞–≤–∞–љ–µ, —В–Њ–≤–∞ —Б—К—Й–Њ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ —В–µ –≤—Б—К—Й–љ–Њ—Б—В –љ–µ —Б–∞ –Љ–љ–Њ–≥–Њ –Ї–∞—В–Њ –љ–∞—И–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞, –Ї—К–і–µ—В–Њ –≤ –Є–Ј–≤–µ—Б—В–µ–љ —Б–Љ–Є—Б—К–ї —Б–µ —Б–ї—Г—З–≤–∞ –Љ–љ–Њ–≥–Њ –њ–Њ–≤–µ—З–µ.
–Ф–∞ —А–∞–Ј–≥–ї–µ–і–∞–Љ–µ —Б–ї—Г—З–∞—П:

–Р–Ї–Њ –њ—А–Њ–і—К–ї–ґ–∞–≤–∞–Љ–µ –і–Њ—Б—В–∞—В—К—З–љ–Њ –і—К–ї–≥–Њ, –і–∞–ї–Є —В–Њ–≤–∞ –±–Є –љ–∞–њ—А–∞–≤–Є–ї–Њ –љ–µ—Й–Њ –Ї–∞—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Є –∞–Ї–Њ –і–∞, —Б –Ї–Њ–ї–Ї–Њ –Є–Ј–Љ–µ—А–µ–љ–Є—П?
–Э—Г–ґ–µ–љ –µ –љ—П–Ї–∞–Ї—К–≤ —Б—В–∞–±–Є–ї–µ–љ –љ–∞—З–Є–љ –і–∞ –Є–Ј–Љ–µ—А–Є–Љ –Є–Ј–Љ–µ—А–µ–љ–Є–µ—В–Њ. –Ш –≤—Б–µ –њ–∞–Ї –і–∞ –љ–µ –Ј–∞–±—А–∞–≤—П–Љ–µ, —З–µ —В–µ–Ј–Є –Ї–∞—А—В–Є–љ–Ї–Є —Б–∞ —Б–∞–Љ–Њ –≤–Є–Ј—Г–∞–ї–Є–Ј–∞—Ж–Є–Є - –Њ—Б–љ–Њ–≤–љ–∞—В–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –і–Є—Б–Ї—А–µ—В–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П, –Њ–њ—А–µ–і–µ–ї—П—Й–Є —Е–Є–њ–µ—А–≥—А–∞—Д–∞ - –±–µ–Ј –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—П –Ј–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є, –≥–µ–Њ–Љ–µ—В—А–Є—П –Є–ї–Є –і–Њ—А–Є —В–Њ–њ–Њ–ї–Њ–≥–Є—П. –Ш –Љ–µ–ґ–і—Г –і—А—Г–≥–Њ—В–Њ, –Ј–∞ –і–∞ —Б–µ –њ–Њ–і—З–µ—А—В–∞–µ —В–Њ–≤–∞ —В–≤—К—А–і–µ–љ–Є–µ, –і–Њ–ї—Г –µ –µ–і–љ–∞ –Є —Б—К—Й–∞ –≥—А–∞—Д–Є–Ї–∞ - —Б –∞–±—Б–Њ–ї—О—В–љ–Њ –µ–і–љ–∞ –Є —Б—К—Й–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –љ–∞ —Б–≤—К—А–Ј–∞–љ–Њ—Б—В - –њ–Њ —З–µ—В–Є—А–Є —А–∞–Ј–ї–Є—З–љ–Є –љ–∞—З–Є–љ–∞:

–Э–Њ –і–∞ —Б–µ –≤—К—А–љ–µ–Љ –Ї—К–Љ –≤—К–њ—А–Њ—Б–∞ –Ј–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–µ—В–Њ, –њ—А–Є–њ–Њ–Љ–љ–µ—В–µ, —З–µ –њ–ї–Њ—Й—В–∞ –љ–∞ –Њ–Ї—А—К–ґ–љ–Њ—Б—В –µ
–Ф–∞ —Б–µ –≤—К—А–љ–µ–Љ –Ї—К–Љ¬†—Е–Є–њ–µ—А–≥—А–∞—Д–∞. –°–ї–µ–і —В–Њ–≤–∞ –і–∞ –њ–Њ—Б–ї–µ–і–≤–∞–Љ–µ


–Ш –∞–Ї–Њ —Б–µ–≥–∞ –њ—А–µ–±—А–Њ–Є—В–µ –±—А–Њ—П –љ–∞ —В–Њ—З–Ї–Є—В–µ, –і–Њ—Б—В–Є–≥–љ–∞—В–Є –њ—А–µ–Љ–Є–љ–∞–≤–∞–є–Ї–Є вАЮ—А–∞–Ј—Б—В–Њ—П–љ–Є–µ
–Ґ–∞–Ї–∞ —З–µ —В–Њ–≤–∞ –љ–Є –і–∞–≤–∞ –љ–∞—З–Є–љ –і–∞ –Є–Ј–Љ–µ—А–Є–Љ –µ—Д–µ–Ї—В–Є–≤–љ–Њ—В–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ –љ–∞ –љ–∞—И–Є—В–µ —Е–Є–њ–µ—А–≥—А–∞—Д–Є. –Я—А–Њ—Б—В–Њ –Ј–∞–њ–Њ—З–≤–∞–Љ–µ –≤ –Ї–Њ–љ–Ї—А–µ—В–љ–∞ —В–Њ—З–Ї–∞ –Є –≤–Є–ґ–і–∞–Љ–µ –Ї–Њ–ї–Ї–Њ —В–Њ—З–Ї–Є —Б–µ –і–Њ—Б—В–Є–≥–∞—В, –∞–Ї–Њ —Б–µ –љ–∞–њ—А–∞–≤—П—В¬†

–°–µ–≥–∞, –Ј–∞ –і–∞ –љ–∞–Љ–µ—А–Є–Љ –µ—Д–µ–Ї—В–Є–≤–љ–Њ—В–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ, –њ–Њ –њ—А–Є–љ—Ж–Є–њ –њ—А–Њ—Б—В–Њ —В—А—П–±–≤–∞ –і–∞ –њ—А–Є—Б–њ–Њ—Б–Њ–±–Є–Љ —А–µ–Ј—Г–ї—В–∞—В–Є—В–µ –Ї—К–Љ 
–Р–Ї–Њ —Б–µ –љ–∞–њ—А–∞–≤–Є —Б—К—Й–Њ—В–Њ –Ј–∞

—Б–µ —Б—В–Є–≥–∞ –і–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ 2:

–Ъ–∞–Ї–≤–Њ –Њ–Ј–љ–∞—З–∞–≤–∞ –і—А–Њ–±–љ–Њ—В–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ?¬†–Ш–Љ–µ–љ–љ–Њ¬†—Д—А–∞–Ї—В–∞–ї–Є—В–µ –Є–Љ–∞—В –і—А–Њ–±–љ–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П –Є¬† –њ—А–∞–≤–Є–ї–∞—В–∞ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –Љ–Њ–≥–∞—В –ї–µ—Б–љ–Њ –і–∞ –≥–Є —Б—К—Б—В–∞–≤—П—В:
{{


–Р–Ї–Њ –Є–Ј–Љ–µ—А–Є–Љ –Є–Ј–Љ–µ—А–µ–љ–Є–µ—В–Њ —В—Г–Ї, –њ–Њ–ї—Г—З–∞–≤–∞–Љ–µ 1,58 - –Њ–±–Є—З–∞–є–љ–Њ—В–Њ —Д—А–∞–Ї—В–∞–ї–љ–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ

–Я—А–∞–≤–Є–ї–Њ—В–Њ –њ–Њ-–≥–Њ—А–µ –љ–µ —Б—К–Ј–і–∞–≤–∞ —Б—В—А—Г–Ї—В—Г—А–∞, –Ї–Њ—П—В–Њ –µ —В–Њ–ї–Ї–Њ–≤–∞ –њ–Њ–і—А–µ–і–µ–љ–∞ –Ї–∞—В–Њ —В–∞–Ј–Є. –Т—Б—К—Й–љ–Њ—Б—В, –≤—К–њ—А–µ–Ї–Є —З–µ —Б–∞–Љ–Њ—В–Њ –њ—А–∞–≤–Є–ї–Њ –µ –љ–∞–њ—К–ї–љ–Њ –і–µ—В–µ—А–Љ–Є–љ–Є—А–∞–љ–Њ, —Б—В—А—Г–Ї—В—Г—А–∞—В–∞, –Ї–Њ—П—В–Њ —Б—К–Ј–і–∞–≤–∞, –Є–Ј–≥–ї–µ–ґ–і–∞ –і–Њ—Б—В–∞ —Б–ї—Г—З–∞–є–љ–∞. –Э–Њ –Є–Ј–Љ–µ—А–≤–∞–љ–Є—П—В–∞ –њ–Њ–і—Б–Ї–∞–Ј–≤–∞—В, —З–µ –Ї–Њ–≥–∞—В–Њ –њ—А–Њ–і—К–ї–ґ–∞–≤–∞ –і–∞ —Б–µ –Є–Ј–њ—К–ї–љ—П–≤–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ, —В–Њ –њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –µ 2,7-–Љ–µ—А–љ–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ.
–†–∞–Ј–±–Є—А–∞ —Б–µ, 2.7 –љ–µ –µ 3 –Є –≤–µ—А–Њ—П—В–љ–Њ —В–Њ–≤–∞ –Ї–Њ–љ–Ї—А–µ—В–љ–Њ –њ—А–∞–≤–Є–ї–Њ –љ–µ –µ —В—К—А—Б–µ–љ–Њ—В–Њ –њ—А–∞–≤–Є–ї–Њ –Ј–∞ –љ–∞—И–∞—В–∞ –Ї–Њ–љ–Ї—А–µ—В–љ–∞ –≤—Б–µ–ї–µ–љ–∞ (–Љ–∞–Ї–∞—А —З–µ –љ–µ –µ —П—Б–љ–Њ –Ї–∞–Ї–≤–Њ –µ—Д–µ–Ї—В–Є–≤–љ–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ –±–Є –Є–Љ–∞–ї–Њ, –∞–Ї–Њ –≥–Њ –Є–Ј–њ—К–ї–љ–Є–Љ 10 100 —Б—В—К–њ–Ї–Є). –Э–Њ –њ—А–Њ—Ж–µ—Б—К—В –љ–∞ –Є–Ј–Љ–µ—А–≤–∞–љ–µ –љ–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–µ—В–Њ –њ–Њ–Ї–∞–Ј–≤–∞ –њ—А–Є–Љ–µ—А –Ј–∞ —В–Њ–≤–∞ –Ї–∞–Ї –Љ–Њ–ґ–µ–Љ –і–∞ –Ј–∞–њ–Њ—З–љ–µ–Љ –і–∞ –њ—А–∞–≤–Є–Љ вАЮ—Б–≤—К—А–Ј–∞–љ–Є —Б —Д–Є–Ј–Є–Ї–∞—В–∞вАЬ —В–≤—К—А–і–µ–љ–Є—П –Ј–∞ –њ–Њ–≤–µ–і–µ–љ–Є–µ—В–Њ –љ–∞ –њ—А–∞–≤–Є–ї–∞—В–∞.
–Т–Њ–ї—Д—А–∞–Љ –Њ–±–∞—З–µ –≥–Њ–≤–Њ—А–Є –љ–µ —Б–∞–Љ–Њ –Ј–∞ вАЮ—Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–ЊвАЬ —Б –љ–µ–≥–Њ–≤–Є—В–µ –Љ–Њ–і–µ–ї–Є, —В–Њ–є —Б–µ –Њ–њ–Є—В–≤–∞ –љ–µ —Б–∞–Љ–Њ –і–∞ –љ–∞–њ—А–∞–≤–Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ, –∞ —Б–µ –Њ–њ–Є—В–≤–∞ –і–∞ –љ–∞–њ—А–∞–≤–Є –≤—Б–Є—З–Ї–Њ –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞. –Т —Б—В–∞–љ–і–∞—А—В–љ–∞—В–∞ —Б—К–≤—А–µ–Љ–µ–љ–љ–∞ —Д–Є–Ј–Є–Ї–∞ –Є–Љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ - –Њ–њ–Є—Б–∞–љ–Њ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –Ї–∞—В–Њ –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ* - –Є —Б–ї—Г–ґ–µ—Й–Њ –Ї–∞—В–Њ –µ–і–Є–љ –≤–Є–і —Д–Њ–љ, —Б—А–µ–і–∞, –∞ —Б–ї–µ–і —В–Њ–≤–∞ –µ –≤—Б–Є—З–Ї–Њ, –Ї–Њ–µ—В–Њ –µ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ, —Ж—П–ї–∞—В–∞ –Љ–∞—В–µ—А–Є—П, —З–∞—Б—В–Є—Ж–Є –Є –њ–ї–∞–љ–µ—В–Є –Є —В.–љ.
*–Ь–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ—В–Њ –µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ –њ–Њ–љ—П—В–Є–µ, –Њ–±–Њ–±—Й–∞–≤–∞—Й–Њ –Ј–∞ –Ї–Њ–µ –і–∞ –µ –Є–Ј–Љ–µ—А–µ–љ–Є–µ –њ–Њ–љ—П—В–Є—П—В–∞ –Ј–∞ –ї–Є–љ–Є–Є, –њ–Њ–≤—К—А—Е–љ–Њ—Б—В–Є (–∞ –Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞), –љ–µ —Б—К–і—К—А–ґ–∞—Й–Є –Њ—Б–Њ–±–µ–љ–Є —В–Њ—З–Ї–Є (–±–µ–Ј —В–Њ—З–Ї–Є –љ–∞ —Б–∞–Љ–Њ–њ—А–µ—Б–µ—З–∞–љ–µ, –Ї—А–∞–є–љ–Є —В–Њ—З–Ї–Є –Є –і—А.). –Ч–∞ –њ—А–Є–Љ–µ—А –Ј–∞ –µ–і–љ–Њ–Љ–µ—А–љ–Њ –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ –Љ–Њ–ґ–µ –і–∞ —Б–ї—Г–ґ–Є –њ—А–∞–≤–∞—В–∞, –Њ–Ї—А—К–ґ–љ–Њ—Б—В—В–∞, –µ–ї–Є–њ—Б–∞—В–∞ –Є –≤—К–Њ–±—Й–µ –≤—Б—П–Ї–∞ –ї–Є–љ–Є—П, —З–Є–Є—В–Њ —В–Њ—З–Ї–Є, –Ј–∞–µ–і–љ–Њ —Б –Њ–Ї–Њ–ї–љ–Њ—Б—В–∞ —Б–Є –Њ—В —Б—К—Б–µ–і–љ–Є —В–Њ—З–Ї–Є —Б–∞ –≤–Ј–∞–Є–Љ–љ–Њ –µ–і–љ–Њ–Ј–љ–∞—З–љ–Є –Є –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Є –Є–ї–Є, –Ї–∞–Ї—В–Њ –Ї–∞–Ј–≤–∞—В –≤ —В–Њ–њ–Њ–ї–Њ–≥–Є—П—В–∞,
–Э–Њ –≤ –љ–∞—И–Є—В–µ –Љ–Њ–і–µ–ї–Є –≤ –Є–Ј–≤–µ—Б—В–µ–љ —Б–Љ–Є—Б—К–ї –љ—П–Љ–∞ –љ–Є—Й–Њ –і—А—Г–≥–Њ –Њ—Б–≤–µ–љ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ - –Є –≤ –Є–Ј–≤–µ—Б—В–µ–љ —Б–Љ–Є—Б—К–ї –≤—Б–Є—З–Ї–Њ –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞ —В—А—П–±–≤–∞ –і–∞ –±—К–і–µ вАЮ–љ–∞–њ—А–∞–≤–µ–љ–Њ –Њ—В –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–ЊвАЬ. –Ш–ї–Є –Ї–∞–Ј–∞–љ–Њ –њ–Њ –і—А—Г–≥ –љ–∞—З–Є–љ, —В–Њ—З–љ–Њ —Б—К—Й–Є—П—В —Е–Є–њ–µ—А–≥—А–∞—Д –љ–Є –і–∞–≤–∞ —Б—В—А—Г–Ї—В—Г—А–∞—В–∞ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є –≤—Б–Є—З–Ї–Њ, –Ї–Њ–µ—В–Њ —Б—К—Й–µ—Б—В–≤—Г–≤–∞ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ.
–Ґ–Њ–≤–∞ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ –љ–∞–њ—А–Є–Љ–µ—А —З–∞—Б—В–Є—Ж–∞ –Ї–∞—В–Њ –µ–ї–µ–Ї—В—А–Њ–љ –Є–ї–Є —Д–Њ—В–Њ–љ —В—А—П–±–≤–∞ –і–∞ –Њ—В–≥–Њ–≤–∞—А—П –љ–∞ –љ—П–Ї–∞–Ї–≤–∞ –ї–Њ–Ї–∞–ї–љ–∞ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–∞ –љ–∞ —Е–Є–њ–µ—А–≥—А–∞—Д–∞, –Љ–∞–ї–Ї–Њ –Ї–∞—В–Њ –≤ —В–Њ–Ј–Є –њ—А–Є–Љ–µ—А:

–°–њ–Њ—А–µ–і –Т–Њ–ї—Д—А–∞–Љ¬†10 200 –њ—К—В–Є –њ–Њ–≤–µ—З–µ вАЮ–∞–Ї—В–Є–≤–љ–Њ—Б—ВвАЬ –≤ —Е–Є–њ–µ—А–≥—А–∞—Д–∞, –Ї–Њ–є—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –љ–∞—И–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞, –Њ—В–Є–≤–∞ –њ–Њ-—Б–Ї–Њ—А–Њ –Ј–∞ вАЮ–њ–Њ–і–і—К—А–ґ–∞–љ–µ –љ–∞ —Б—В—А—Г–Ї—В—Г—А–∞—В–∞ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–ЊвАЬ, –Њ—В–Ї–Њ–ї–Ї–Њ—В–Њ –Ј–∞ –њ–Њ–і–і—К—А–ґ–∞–љ–µ –љ–∞ —Ж—П–ї–∞—В–∞ –Љ–∞—В–µ—А–Є—П, –Ї–Њ—П—В–Њ —Б—К—Й–µ—Б—В–≤—Г–≤–∞ –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞.
–Ъ—А–Є–≤–Є–љ–∞—В–∞ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є —Г—А–∞–≤–љ–µ–љ–Є—П—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ
–Х—В–Њ –љ—П–Ї–Њ–ї–Ї–Њ —Б—В—А—Г–Ї—В—Г—А–Є, —Б—К–Ј–і–∞–і–µ–љ–Є –Њ—В –њ—А–Њ—Б—В–Є –њ—А–∞–≤–Є–ї–∞:

–Т—Б–Є—З–Ї–Є —В–µ –Є–Ј–≥–ї–µ–ґ–і–∞—В –Ї–∞—В–Њ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В–Є, –љ–Њ –Њ—З–µ–≤–Є–і–љ–Њ –≤—Б–Є—З–Ї–Є —Б–∞ —А–∞–Ј–ї–Є—З–љ–Є. –Ш –µ–і–Є–љ –Њ—В –љ–∞—З–Є–љ–Є—В–µ –Ј–∞ —Е–∞—А–∞–Ї—В–µ—А–Є–Ј–Є—А–∞–љ–µ—В–Њ –Є–Љ –µ —З—А–µ–Ј —В—П—Е–љ–∞—В–∞ –ї–Њ–Ї–∞–ї–љ–∞ –Ї—А–Є–≤–Є–љ–∞. –Ю–Ї–∞–Ј–≤–∞ —Б–µ, —З–µ –≤ –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞¬†–Т–Њ–ї—Д—А–∞–Љ –Ї—А–Є–≤–Є–љ–∞—В–∞ –µ –њ–Њ–љ—П—В–Є–µ, —В—П—Б–љ–Њ —Б–≤—К—А–Ј–∞–љ–Њ —Б –Є–Ј–Љ–µ—А–µ–љ–Є–µ—В–Њ - –Є —В–Њ–Ј–Є —Д–∞–Ї—В –≤—Б—К—Й–љ–Њ—Б—В —Й–µ –±—К–і–µ –Љ–љ–Њ–≥–Њ –≤–∞–ґ–µ–љ –Ј–∞ —А–∞–Ј–±–Є—А–∞–љ–µ—В–Њ, –љ–∞–њ—А–Є–Љ–µ—А –Ї–∞–Ї –≤—К–Ј–љ–Є–Ї–≤–∞ –≥—А–∞–≤–Є—В–∞—Ж–Є—П—В–∞.
–Ш —В–∞–Ї–∞ –Ї–∞–Ї –Љ–Њ–ґ–µ –і–∞ —Б–µ¬†–Є–Ј–Љ–µ—А–Є¬†–Ї—А–Є–≤–Є–љ–∞—В–∞ –љ–∞ —Е–Є–њ–µ—А–≥—А–∞—Д. –Ю–±–Є–Ї–љ–Њ–≤–µ–љ–Њ –њ–ї–Њ—Й—В–∞ –љ–∞ –Њ–Ї—А—К–ґ–љ–Њ—Б—В –µ

–Ґ–∞–Ј–Є –Њ–±–ї–∞—Б—В –≤–µ—З–µ –љ–µ –µ
¬†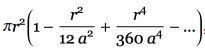 , –Ї—К–і–µ—В–Њ
, –Ї—К–і–µ—В–Њ
–Р–Ї–Њ –Њ–±–Њ–±—Й–Є–Љ –і–Њ
![]() , –Ї—К–і–µ—В–Њ
, –Ї—К–і–µ—В–Њ
–Т—Б–Є—З–Ї–Њ —В–Њ–≤–∞ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ –∞–Ї–Њ —А–∞–Ј–≥–ї–µ–і–∞–Љ–µ —В–µ–Љ–њ–Њ–≤–µ—В–µ –љ–∞ —А–∞—Б—В–µ–ґ –љ–∞ —Б—Д–µ—А–Є—З–љ–Є—В–µ —В–Њ–њ–Ї–Є –≤ —Е–Є–њ–µ—А–≥—А–∞—Д–Єte, –Љ–Њ–ґ–µ–Љ –і–∞ –Њ—З–∞–Ї–≤–∞–Љ–µ –і–≤–∞ –њ—А–Є–љ–Њ—Б–∞: –≤–Њ–і–µ—Й –Њ—В –њ–Њ—А—П–і—К–Ї–∞
–Х—В–Њ –њ—А–Є–Љ–µ—А. –Т–Љ–µ—Б—В–Њ –і–∞ –і–∞–≤–∞–Љ–µ –њ–ї–Њ—Б–Ї–∞ –Њ—Ж–µ–љ–Ї–∞ –љ–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–µ—В–Њ (—В—Г–Ї —А–∞–≤–љ–∞ –љ–∞ 2), –Є–Љ–∞–Љ–µ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –љ–∞–Љ–∞–ї—П–≤–∞, –Њ—В—А–∞–Ј—П–≤–∞–є–Ї–Є –њ–Њ–ї–Њ–ґ–Є—В–µ–ї–љ–∞—В–∞ (вАЮ—Б—Д–µ—А–Њ–њ–Њ–і–Њ–±–љ–∞вАЬ) –Ї—А–Є–≤–Є–љ–∞ –љ–∞ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞:

–Ъ–∞–Ї–≤–Њ –µ –Ј–љ–∞—З–µ–љ–Є–µ—В–Њ –љ–∞ –Ї—А–Є–≤–Є–љ–∞—В–∞? –Х–і–љ–Њ –µ, —З–µ –Є–Љ–∞ –Ј–љ–∞—З–µ–љ–Є–µ –Ј–∞ –≥–µ–Њ–і–µ–Ј–Є—З–љ–∞—В–∞ –ї–ЄћБ–љ–Є—П. –У–µ–Њ–і–µ–Ј–Є—З–љ–∞—В–∞ –ї–Є–љ–Є—П –µ –љ–∞–є-–Ї—К—Б–Њ—В–Њ —А–∞–Ј—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –і–≤–µ —В–Њ—З–Ї–Є. –Т –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ—В–Њ –њ–ї–Њ—Б–Ї–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –≥–µ–Њ–і–µ–Ј–Є—З–љ–∞—В–∞ –ї–Є–љ–Є—П –µ –њ—А–Њ—Б—В–Њ –ї–Є–љ–Є—П. –Э–Њ –Ї–Њ–≥–∞—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є–Љ–∞ –Ї—А–Є–≤–Є–љ–∞, –≥–µ–Њ–і–µ–Ј–Є—З–љ–∞—В–∞ –ї–Є–љ–Є—П –µ –Є–Ј–≤–Є—В–∞:

–Т —Б–ї—Г—З–∞—П –љ–∞ –њ–Њ–ї–Њ–ґ–Є—В–µ–ї–љ–∞ –Ї—А–Є–≤–Є–љ–∞ —Б–љ–Њ–њ–Њ–≤–µ—В–µ –≥–µ–Њ–і–µ–Ј–Є—З–љ–Є –ї–ЄћБ–љ–Є–Є —Б–µ —А–∞–Ј–і–µ–ї—П—В –Є —Б—К–±–Є—А–∞—В, –Ј–∞ –Њ—В—А–Є—Ж–∞—В–µ–ї–љ–∞—В–∞ –Ї—А–Є–≤–Є–љ–∞ —В–µ —Б–µ —Б–±–ї–Є–ґ–∞–≤–∞—В. –Э–Њ –і–Њ–±—А–µ, –≤—К–њ—А–µ–Ї–Є —З–µ –њ—К—А–≤–Њ–љ–∞—З–∞–ї–љ–Њ –≥–µ–Њ–і–µ–Ј–Є—З–љ–Є—В–µ –ї–Є–љ–Є–Є —Б–∞ –±–Є–ї–Є –і–µ—Д–Є–љ–Є—А–∞–љ–Є –Ј–∞ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ (–≤—Б—К—Й–љ–Њ—Б—В, –Ї–∞–Ї—В–Њ –њ–Њ–і—Б–Ї–∞–Ј–≤–∞ –Є–Љ–µ—В–Њ, —В–µ —Б–∞ –і–µ—Д–Є–љ–Є—А–∞–љ–Є –Ј–∞ –њ—К—В–µ–Ї–Є –њ–Њ –њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞ –љ–∞ –Ч–µ–Љ—П—В–∞),¬†—В–µ –Љ–Њ–≥–∞—В –і–∞ —Б–µ –Њ–њ—А–µ–і–µ–ї—П—В¬†–Є –Ј–∞ –≥—А–∞—Д–Є (–Є —Е–Є–њ–µ—А–≥—А–∞—Д–Є). –Ш –Њ—В–љ–Њ–≤–Њ –≥–µ–Њ–і–µ–Ј–Є—З–љ–Є—В–µ –ї–Є–љ–Є–Є¬†—Б–∞ –љ–∞–є-–Ї—А–∞—В–Ї–Є—П—В –њ—К—В –Љ–µ–ґ–і—Г –і–≤–µ —В–Њ—З–Ї–Є –≤ –≥—А–∞—Д (–Є–ї–Є —Е–Є–њ–µ—А–≥—А–∞—Д).
–Х—В–Њ –≥–µ–Њ–і–µ–Ј–Є—З–љ–Є—В–µ –ї–Є–љ–Є–Є –љ–∞ вАЮ–њ–Њ–≤—К—А—Е–љ–Њ—Б—В—В–∞ —Б –њ–Њ–ї–Њ–ґ–Є—В–µ–ї–љ–∞ –Ї—А–Є–≤–Є–љ–∞вАЬ, —Б—К–Ј–і–∞–і–µ–љ–∞ –њ–Њ –µ–і–љ–Њ –Њ—В –њ—А–∞–≤–Є–ї–∞—В–∞:

–Ш –µ—В–Њ –≥–Є –Ј–∞ –њ–Њ-—Б–ї–Њ–ґ–љ–∞ —Б—В—А—Г–Ї—В—Г—А–∞:

–Ч–∞—Й–Њ —Б–∞ –≤–∞–ґ–љ–Є –≥–µ–Њ–і–µ–Ј–Є—З–љ–Є—В–µ –ї–Є–љ–Є–Є? –Х–і–љ–∞ –Њ—В –њ—А–Є—З–Є–љ–Є—В–µ –µ, —З–µ –≤ –Ю–±—Й–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ —В–Њ–≤–∞ —Б–∞ —В—А–∞–µ–Ї—В–Њ—А–Є–Є—В–µ, –Ї–Њ–Є—В–Њ —Б–≤–µ—В–ї–Є–љ–∞—В–∞ (–Є–ї–Є "—Б–≤–Њ–±–Њ–і–љ–Њ –њ–∞–і–∞—Й" –Њ–±–µ–Ї—В) —Б–ї–µ–і–≤–∞ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ. –Ш –≤ —В–∞–Ј–Є —В–µ–Њ—А–Є—П –≥—А–∞–≤–Є—В–∞—Ж–Є—П—В–∞ —Б–µ —Б–≤—К—А–Ј–≤–∞ —Б—К—Б –Ї—А–Є–≤–Є–љ–∞—В–∞ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ. –Ґ–∞–Ї–∞ —З–µ, –Ї–Њ–≥–∞—В–Њ –µ–і–Є–љ –Њ–±–µ–Ї—В —Б–µ –Њ—В–Ї–ї–Њ–љ–Є, –Ј–∞–Њ–±–Є–Ї–∞–ї—П–є–Ї–Є –°–ї—К–љ—Ж–µ—В–Њ, —В–Њ–≤–∞ —Б–µ —Б–ї—Г—З–≤–∞, –Ј–∞—Й–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Њ–Ї–Њ–ї–Њ –°–ї—К–љ—Ж–µ—В–Њ –µ –Є–Ј–Ї—А–Є–≤–µ–љ–Њ, —В–∞–Ї–∞ —З–µ –≥–µ–Њ–і–µ–Ј–Є—З–љ–∞—В–∞ –ї–Є–љ–Є—П, –Ї–Њ—П—В–Њ –Њ–±–µ–Ї—В—К—В —Б–ї–µ–і–≤–∞, —Б—К—Й–Њ –µ –Є–Ј–≤–Є—В–∞.
–Ю–њ–Є—Б–∞–љ–Є–µ—В–Њ –љ–∞ –Ю–±—Й–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ –љ–∞ –Ї—А–Є–≤–Є–љ–∞—В–∞ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ —Б–µ –Њ—Б–љ–Њ–≤–∞–≤–∞ –љ–∞ —Б–Ї–∞–ї–∞—А–љ–∞—В–∞ –Ї—А–Є–≤–Є–љ–∞
–Т —В–∞–Ј–Є –Ј–∞–і–∞—З–∞ —Б–њ–Њ—А–µ–і –Т–Њ–ї—Д—А–∞–Љ¬†–Є–Љ–∞ "–Љ–∞–ї–Ї–Њ"¬†–Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—В–∞ —Б–ї–Њ–ґ–љ–Њ—Б—В - —В—А—П–±–≤–∞ –і–∞ —Б–µ –≤–Ј–µ–Љ–µ –њ—А–µ–і–≤–Є–і –Ї—А–Є–≤–Є–љ–∞—В–∞¬†–љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ + –≤—А–µ–Љ–µ—В–Њ, –∞ –љ–µ —Б–∞–Љ–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ.
–Ш –і–∞! –Ъ–Њ–ї–Ї–Њ—В–Њ –Є –і–∞ –µ —Г–і–Є–≤–Є—В–µ–ї–љ–Њ, –Ј–∞–і–∞—З–∞—В–∞ –µ –Є–Ј–њ—К–ї–љ–µ–љ–∞!
–° —Г—В–Њ—З–љ–µ–љ–Є–µ—В–Њ¬†"–≤ —А–∞–Ј–ї–Є—З–љ–Є –≥—А–∞–љ–Є—Ж–Є –Є –њ—А–Є —А–∞–Ј–ї–Є—З–љ–Є –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є—П" –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –љ–∞–Є—Б—В–Є–љ–∞ –≤—К–Ј–њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞—В —Г—А–∞–≤–љ–µ–љ–Є—П—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ.
"–Т –љ–∞—З–∞–ї–Њ—В–Њ –њ—А–Њ—Б—В–Њ –≤—К–Ј–њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞—Е–Љ–µ —Г—А–∞–≤–љ–µ–љ–Є—П—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ –Ј–∞ –≤–∞–Ї—Г—Г–Љ, –њ–Њ–і—Е–Њ–і—П—Й–Є, –Ї–Њ–≥–∞—В–Њ –љ—П–Љ–∞¬†–Љ–∞—В–µ—А–Є—П (–Є–ї–Є –µ –њ—А–µ–љ–µ–±—А–µ–ґ–Є–Љ–∞), –љ–Њ –Ї–Њ–≥–∞—В–Њ –Њ–±—Б—К–ґ–і–∞–Љ–µ –Љ–∞—В–µ—А–Є—П—В–∞, —Й–µ –≤–Є–і–Є–Љ, —З–µ –≤—Б—К—Й–љ–Њ—Б—В –њ–Њ–ї—Г—З–∞–≤–∞–Љ–µ –њ—К–ї–љ–Є—В–µ —Г—А–∞–≤–љ–µ–љ–Є—П –љ–∞ –Р–є–љ—Й–∞–є–љ", —А–∞–Ј–Ї–∞–Ј–≤–∞¬†–Т–Њ–ї—Д—А–∞–Љ.
–Ф–∞ —Б–µ –≤—К–Ј–њ—А–Њ–Є–Ј–≤–µ–і–∞—В —Г—А–∞–≤–љ–µ–љ–Є—П—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ –µ –≥–Њ–ї—П–Љ–Њ –њ–Њ—Б—В–Є–ґ–µ–љ–Є–µ.
–°—В—А—Г–≤–∞ —Б–Є –і–∞ —Б–µ –Ї–∞–ґ–µ –Љ–∞–ї–Ї–Њ –Ј–∞ —В–Њ–≤–∞ –Ї–∞–Ї —А–∞–±–Њ—В–Є –і–Є—Д–µ—А–µ–љ—Ж–Є—А–∞–љ–µ—В–Њ. –Ґ–Њ–≤–∞ –≤—Б—К—Й–љ–Њ—Б—В –µ –і–Њ–љ—П–Ї—К–і–µ –∞–љ–∞–ї–Њ–≥–Є—З–љ–Њ –љ–∞ –Є–Ј–≤–µ–ґ–і–∞–љ–µ—В–Њ –љ–∞ —Г—А–∞–≤–љ–µ–љ–Є—П—В–∞ –љ–∞ –њ–Њ—В–Њ–Ї —Д–ї—Г–Є–і–Є¬†–Њ—В –≥—А–∞–љ–Є—Ж–∞—В–∞ –љ–∞ –±–∞–Ј–Њ–≤–∞—В–∞ –і–Є–љ–∞–Љ–Є–Ї–∞ –љ–∞ –Љ–љ–Њ–≥–Њ –і–Є—Б–Ї—А–µ—В–љ–Є –Љ–Њ–ї–µ–Ї—Г–ї–Є. –Э–Њ –≤ —Б–ї—Г—З–∞—П –µ–Ї–Є–њ—К—В –Є–Ј—З–Є—Б–ї—П–≤–∞ –Є–Љ–µ–љ–љ–Њ —Б—В—А—Г–Ї—В—Г—А–∞—В–∞ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ, –∞ –љ–µ —Б–Ї–Њ—А–Њ—Б—В—В–∞ –љ–∞ —Д–ї—Г–Є–і. –Ґ–Њ–є –Њ–±–∞—З–µ –≤–Ї–ї—О—З–≤–∞ –љ—П–Ї–Њ–Є –Њ—В —Б—К—Й–Є—В–µ –≤–Є–і–Њ–≤–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –њ—А–Є–±–ї–Є–ґ–µ–љ–Є—П –Є –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є—П. –І–Њ–≤–µ–Ї —В—А—П–±–≤–∞ –і–∞ –њ—А–Є–µ–Љ–µ –љ–∞–њ—А–Є–Љ–µ—А, —З–µ –Є–Љ–∞ –і–Њ—Б—В–∞—В—К—З–љ–Њ –µ—Д–µ–Ї—В–Є–≤–љ–∞ —Б–ї—Г—З–∞–є–љ–Њ—Б—В, –≥–µ–љ–µ—А–Є—А–∞–љ–∞ –≤ —Б–Є—Б—В–µ–Љ–∞—В–∞, –Ј–∞ –і–∞ —А–∞–±–Њ—В—П—В —Б—В–∞—В–Є—Б—В–Є—З–µ—Б–Ї–Є—В–µ —Б—А–µ–і–љ–Є —Б—В–Њ–є–љ–Њ—Б—В–Є. –Ш–Љ–∞ –Є —Ж—П–ї –љ–∞–±–Њ—А –Њ—В —Д–Є–љ–Є –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є –≥—А–∞–љ–Є—Ж–Є, –Ї–Њ–Є—В–Њ —В—А—П–±–≤–∞ –і–∞ —Б–µ –≤–Ј–µ–Љ–∞—В –њ—А–µ–і–≤–Є–і. –†–∞–Ј—Б—В–Њ—П–љ–Є—П—В–∞ —В—А—П–±–≤–∞ –і–∞ —Б–∞ –≥–Њ–ї–µ–Љ–Є –≤ —Б—А–∞–≤–љ–µ–љ–Є–µ —Б –Њ—В–і–µ–ї–љ–Є—В–µ —Е–Є–њ–µ—А–≥—А–∞—Д—Б–Ї–Є –≤—А—К–Ј–Ї–Є, –љ–Њ –Љ–∞–ї–Ї–Є –≤ —Б—А–∞–≤–љ–µ–љ–Є–µ —Б —Ж–µ–ї–Є—П —А–∞–Ј–Љ–µ—А –љ–∞ —Е–Є–њ–µ—А–≥—А–∞—Д–∞ –Є —В.–љ.
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—П—В –∞–љ–∞–ї–Є–Ј –љ–∞ "–±–µ–Ј–Ї—А–∞–є–љ–Њ –Љ–∞–ї–Ї–Є—В–µ", —Б—К—З–µ—В–∞–≤–∞—Й –і–Є—Д–µ—А–µ–љ—Ж–Є–∞–ї–љ–Њ—В–Њ –Є –Є–љ—В–µ–≥—А–∞–ї–љ–Њ—В–Њ —Б–Љ—П—В–∞–љ–µ, –µ –Є–Ј–≥—А–∞–і–µ–љ –і–∞ —А–∞–±–Њ—В–Є –≤ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Є –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ (–Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є—П, –Ї–Њ–Є—В–Њ –ї–Њ–Ї–∞–ї–љ–Њ –њ—А–Є–±–ї–Є–ґ–∞–≤–∞—В –µ–≤–Ї–ї–Є–і–Њ–≤–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ). –Э–Њ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –Є–Љ–∞–Љ–µ —В—Г–Ї, –µ –љ–µ—Й–Њ —А–∞–Ј–ї–Є—З–љ–Њ¬†-¬† –љ–∞¬†–≥—А–∞–љ–Є—Ж–∞—В–∞¬†—Б–Є –±–µ–Ј–Ї—А–∞–є–љ–Њ –≥–Њ–ї—П–Љ —Е–Є–њ–µ—А–≥—А–∞—Д –µ –Ї–∞—В–Њ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ, –љ–Њ –Њ–±–Є–Ї–љ–Њ–≤–µ–љ–Њ—В–Њ –Є–Ј—З–Є—Б–ї–µ–љ–Є–µ –љ–µ —А–∞–±–Њ—В–Є¬†–Ј–∞ –љ–µ–≥–Њ (–љ–µ –љ–∞ –њ–Њ—Б–ї–µ–і–љ–Њ –Љ—П—Б—В–Њ, –Ј–∞—Й–Њ—В–Њ –љ—П–Љ–∞¬†–љ–µ–њ—А–µ–Љ–µ–љ–љ–Њ —Ж–µ–ї–Њ—З–Є—Б–ї–µ–љ–Њ –Є–Ј–Љ–µ—А–µ–љ–Є–µ). –Ч–∞—В–Њ–≤–∞¬†–µ –љ—Г–ґ–љ–Њ –љ–µ—Й–Њ, –Ї–Њ–µ—В–Њ –µ –Ї–∞—В–Њ –Њ–±–Њ–±—Й–µ–љ–Є–µ –љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є—П –∞–љ–∞–ї–Є–Ј, –Ї–Њ–µ—В–Њ –µ –љ–∞–њ—А–Є–Љ–µ—А —Б–њ–Њ—Б–Њ–±–љ–Њ –і–∞ —Б–µ —Б–њ—А–∞–≤–Є —Б –Ї—А–Є–≤–Є–љ–∞—В–∞ –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–∞ —Б –і—А–Њ–±–љ–Є –Є–Ј–Љ–µ—А–µ–љ–Є—П. (–Э–∞–є-–±–ї–Є–Ј–Ї–∞ –і–Њ —В–Њ–≤–∞ –µ —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—В–µ –≥—А—Г–њ–Є.)
–Ґ—А—П–±–≤–∞¬†–і–∞ —Б–µ –Њ—В–±–µ–ї–µ–ґ–Є, —З–µ –Є–Љ–∞ –Љ–љ–Њ–≥–Њ —В—К–љ–Ї–Њ—Б—В–Є –≤ –њ—А–µ—Ж–Є–Ј–љ–Є—П –Ї–Њ–Љ–њ—А–Њ–Љ–Є—Б –Љ–µ–ґ–і—Г –њ—А–Њ–Љ—П–љ–∞—В–∞ –љ–∞ –Є–Ј–Љ–µ—А–µ–љ–Є–µ—В–Њ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є –Ї—А–Є–≤–Є–љ–∞—В–∞ –≤ –љ–µ–≥–Њ. –Ш –Љ–∞–Ї–∞—А –і–∞ —Б–µ –Љ–Є—Б–ї–Є–Љ, —З–µ –љ–∞—И–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞ –µ —В—А–Є–Є–Ј–Љ–µ—А–љ–∞, —Б–њ–Њ—А–µ–і –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –µ –љ–∞–њ—К–ї–љ–Њ –≤—К–Ј–Љ–Њ–ґ–љ–Њ –і–∞ –Є–Љ–∞ –њ–Њ–љ–µ –ї–Њ–Ї–∞–ї–љ–Є –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П - –Є –љ–∞–є-–≤–µ—А–Њ—П—В–љ–Њ –≤ –і–µ–є—Б—В–≤–Є—В–µ–ї–љ–Њ—Б—В –µ –Є–Љ–∞–ї–Њ –≥–Њ–ї–µ–Љ–Є –Њ—В–Ї–ї–Њ–љ–µ–љ–Є—П –≤ —А–∞–љ–љ–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞.
–Т—А–µ–Љ–µ—В–Њ
–Т –љ–∞—И–Є—В–µ –Љ–Њ–і–µ–ї–Є –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ —Б–µ –Њ–њ—А–µ–і–µ–ї—П –Њ—В –Љ–∞—Й–∞–±–љ–∞—В–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –љ–∞ —Е–Є–њ–µ—А–≥—А–∞—Д, –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞—Й –Ї–Њ–ї–µ–Ї—Ж–Є—П –Њ—В –∞–±—Б—В—А–∞–Ї—В–љ–Є –Њ—В–љ–Њ—И–µ–љ–Є—П.
–Э–Њ –Ї–∞–Ї–≤–Њ —В–Њ–≥–∞–≤–∞ –µ –≤—А–µ–Љ–µ—В–Њ?
"–Я—А–µ–Ј –Љ–Є–љ–∞–ї–Є—П –≤–µ–Ї –≤—К–≤ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї–љ–∞—В–∞ —Д–Є–Ј–Є–Ї–∞ –µ –≤—Б–µ–Њ–±—Й–Њ –њ—А–Є–µ—В–Њ, —З–µ –≤—А–µ–Љ–µ—В–Њ –µ –≤ –љ—П–Ї–∞–Ї—К–≤ —Б–Љ–Є—Б—К–ї вАЮ–њ–Њ–і–Њ–±–љ–Њ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–ЊвАЬ - –Є —З–µ —В—А—П–±–≤–∞ –љ–∞–њ—А–Є–Љ–µ—А –і–∞ –љ–µ —Б–µ —А–∞–Ј–і–µ–ї—П—В –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Є –≤—А–µ–Љ–µ, –∞ –і–∞ —Б–µ –≥–Њ–≤–Њ—А–Є –Ј–∞ вАЮ–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–Њ-–≤—А–µ–Љ–µ–≤–Є –Ї–Њ–љ—В–Є–љ—Г—Г–ЉвАЬ. –Ш —Б—К—Б —Б–Є–≥—Г—А–љ–Њ—Б—В —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ —Б–Њ—З–Є –≤ —В–∞–Ј–Є –њ–Њ—Б–Њ–Ї–∞. –Э–Њ –∞–Ї–Њ –≤ –Љ–Є–љ–∞–ї–Є—П –≤–µ–Ї –µ –Є–Љ–∞–ї–Њ –µ–і–Є–љ вАЮ–≥—А–µ—И–µ–љ –Њ–±—А–∞—ВвАЬ –≤ –Є—Б—В–Њ—А–Є—П—В–∞ –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞, –Љ–Є—Б–ї—П, —З–µ —В–Њ–≤–∞ –µ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ—В–Њ, —З–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є –≤—А–µ–Љ–µ—В–Њ —Б–∞ –µ–і–љ–Њ –Є —Б—К—Й–Њ –љ–µ—Й–Њ. –Р –њ—А–Є –љ–∞—И–Є—В–µ –Љ–Њ–і–µ–ї–Є —В–µ –љ–µ —Б–∞ - –≤—К–њ—А–µ–Ї–Є —З–µ, –Ї–∞–Ї—В–Њ —Й–µ –≤–Є–і–Є–Љ, –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ –Њ—В–ї–Є—З–љ–Њ", –Ї–∞–Ј–≤–∞ –Т–Њ–ї—Д—А–∞–Љ.
–Ґ–Њ–≥–∞–≤–∞¬†–Ї–∞–Ї–≤–Њ –µ –≤—А–µ–Љ–µ—В–Њ?
–Т—Б—К—Й–љ–Њ—Б—В —В–Њ–≤–∞ –µ –Љ–љ–Њ–≥–Њ –њ–Њ–і–Њ–±–љ–Њ –љ–∞ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –Ј–љ–∞–µ–Љ –Њ—В –Њ–њ–Є—В: –љ–µ—Г–Љ–Њ–ї–Є–Љ–Є—П—В¬†—Е–Њ–і –љ–∞ –љ–µ—Й–∞—В–∞, –Ї–Њ–Є—В–Њ —Б–µ —Б–ї—Г—З–≤–∞—В –Є –≤–Њ–і—П—В –і–Њ –і—А—Г–≥–Є –љ–µ—Й–∞. –Э–Њ –≤ –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ¬†–≤—А–µ–Љ–µ—В–Њ –µ –љ–µ—Й–Њ –Љ–љ–Њ–≥–Њ –њ–Њ-–њ—А–µ—Ж–Є–Ј–љ–Њ: —В–Њ–≤–∞ –µ –њ—А–Њ–≥—А–µ—Б–Є–≤–љ–Њ—В–Њ –њ—А–Є–ї–∞–≥–∞–љ–µ –љ–∞ –њ—А–∞–≤–Є–ї–∞, –Ї–Њ–Є—В–Њ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–Њ –њ—А–Њ–Љ–µ–љ—П—В –∞–±—Б—В—А–∞–Ї—В–љ–∞—В–∞ —Б—В—А—Г–Ї—В—Г—А–∞, –Ї–Њ—П—В–Њ –Њ–њ—А–µ–і–µ–ї—П —Б—К–і—К—А–ґ–∞–љ–Є–µ—В–Њ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞.
–Т–µ—А—Б–Є—П—В–∞ –љ–∞ –≤—А–µ–Љ–µ—В–Њ –≤ –љ–∞—И–Є—В–µ –Љ–Њ–і–µ–ї–Є –µ –≤ –Є–Ј–≤–µ—Б—В–µ–љ —Б–Љ–Є—Б—К–ї –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞, –Ї–Њ–Љ–њ—О—В—К—А–љ–∞. –° —В–µ—З–µ–љ–Є–µ –љ–∞ –≤—А–µ–Љ–µ—В–Њ –љ–Є–µ –љ–∞ –њ—А–∞–Ї—В–Є–Ї–∞ –≤–Є–ґ–і–∞–Љ–µ —А–µ–Ј—Г–ї—В–∞—В–Є—В–µ –Њ—В –≤—Б–µ –њ–Њ–≤–µ—З–µ –Є –њ–Њ–≤–µ—З–µ —Б—В—К–њ–Ї–Є –≤ –Є–Ј—З–Є—Б–ї–µ–љ–Є–µ—В–Њ. –Ш –і–µ–є—Б—В–≤–Є—В–µ–ї–љ–Њ —Д–µ–љ–Њ–Љ–µ–љ—К—В –љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞—В–∞ –љ–µ–њ—А–Є–≤–Њ–і–Є–Љ–Њ—Б—В –њ—А–µ–і–њ–Њ–ї–∞–≥–∞, —З–µ –Є–Љ–∞ –љ–µ—Й–Њ –Њ–њ—А–µ–і–µ–ї–µ–љ–Њ –Є –љ–µ–њ—А–Є–≤–Њ–і–Є–Љ–Њ вАЮ–њ–Њ—Б—В–Є–≥–љ–∞—В–ЊвАЬ –Њ—В —В–Њ–Ј–Є –њ—А–Њ—Ж–µ—Б. (–љ–∞–њ—А–Є–Љ–µ—А —В–∞–Ј–Є –љ–µ–њ—А–Є–≤–Њ–і–Є–Љ–Њ—Б—В –µ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –µ –Њ—В–≥–Њ–≤–Њ—А–љ–Њ –Ј–∞ вАЮ–Ї—А–Є–њ—В–Є—А–∞–љ–µ—В–ЊвАЬ –љ–∞ –њ—К—А–≤–Њ–љ–∞—З–∞–ї–љ–Є—В–µ —Г—Б–ї–Њ–≤–Є—П, –Ї–Њ–µ—В–Њ –µ —Б–≤—К—А–Ј–∞–љ–Њ —Б—К—Б –Ј–∞–Ї–Њ–љ–∞ –Ј–∞ —Г–≤–µ–ї–Є—З–∞–≤–∞–љ–µ –љ–∞ –µ–љ—В—А–Њ–њ–Є—П—В–∞ –Є —В–µ—А–Љ–Њ–і–Є–љ–∞–Љ–Є—З–љ–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ –љ–∞ –≤—А–µ–Љ–µ—В–Њ.) –Ш–Ј–ї–Є—И–љ–Њ –µ –і–∞ –Ї–∞–Ј–≤–∞–Љ–µ, —З–µ¬†–љ–∞—И–∞—В–∞ —Б—К–≤—А–µ–Љ–µ–љ–љ–∞ –Є–Ј—З–Є—Б–ї–Є—В–µ–ї–љ–∞ –њ–∞—А–∞–і–Є–≥–Љ–∞ –љ–µ –µ —Б—К—Й–µ—Б—В–≤—Г–≤–∞–ї–∞ –њ—А–µ–і–Є –≤–µ–Ї, –Ї–Њ–≥–∞—В–Њ –µ –≤—К–≤–µ–і–µ–љ–Њ –њ–Њ–љ—П—В–Є–µ—В–Њ вАЮ–њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ-–≤—А–µ–Љ–µвАЬ –Є –∞–Ї–Њ —П –Є–Љ–∞—И–µ, –Є—Б—В–Њ—А–Є—П—В–∞ –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞ –Љ–Њ–ґ–µ –±–Є —Й–µ—И–µ –і–∞ –µ –Љ–љ–Њ–≥–Њ —А–∞–Ј–ї–Є—З–љ–∞.
–Т –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –≤—А–µ–Љ–µ—В–Њ –µ –њ—А–Њ—Б—В–Њ –њ—А–Њ–≥—А–µ—Б–Є–≤–љ–Њ—В–Њ –њ—А–Є–ї–∞–≥–∞–љ–µ –љ–∞ –њ—А–∞–≤–Є–ї–∞—В–∞. –Э–Њ –Є–Љ–∞ –µ–і–љ–∞ —В—К–љ–Ї–Њ—Б—В –≤ —В–Њ–≤–∞ –Ї–∞–Ї —В–Њ—З–љ–Њ —А–∞–±–Њ—В–Є —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –≤ –љ–∞—З–∞–ї–Њ—В–Њ –Љ–Њ–ґ–µ –і–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –Љ–∞–ї—К–Ї –і–µ—В–∞–є–ї, –љ–Њ¬† –≤—Б—К—Й–љ–Њ—Б—В —Б–µ –Њ–Ї–∞–Ј–≤–∞ –Њ–≥—А–Њ–Љ–љ–Њ –Є –Ї–ї—О—З—К—В –Ї–∞–Ї—В–Њ –Ї—К–Љ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞, —В–∞–Ї–∞ –Є –Ї—К–Љ –Ї–≤–∞–љ—В–Њ–≤–∞—В–∞ –Љ–µ—Е–∞–љ–Є–Ї–∞.
–Т –љ–∞—З–∞–ї–Њ—В–Њ –љ–∞ —В–∞–Ј–Є —Б—В–∞—В–Є—П –Т–Њ–ї—Д—А–∞–Љ –≥–Њ–≤–Њ—А–Є –Ј–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ
{{

–Є –њ–Њ–Ї–∞–Ј–∞ "–њ—К—А–≤–Є—В–µ –љ—П–Ї–Њ–ї–Ї–Њ —Б—В—К–њ–Ї–Є" –њ—А–Є –њ—А–Є–ї–∞–≥–∞–љ–µ—В–Њ –Љ—Г

–Э–Њ –Ї–∞–Ї —В–Њ—З–љ–Њ —Б–µ –њ—А–Є–ї–∞–≥–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ? –Ъ–∞–Ї–≤–Њ –µ "–≤—К—В—А–µ" –≤ —В–µ–Ј–Є —Б—В—К–њ–Ї–Є? –Я—А–∞–≤–Є–ї–Њ—В–Њ –Њ–њ—А–µ–і–µ–ї—П –Ї–∞–Ї –і–∞ —Б–µ –≤–Ј–µ–Љ–∞—В –і–≤–µ –≤—А—К–Ј–Ї–Є –≤ —Е–Є–њ–µ—А–≥—А–∞—Д–∞ (–Ї–Њ–є—В–Њ –≤ —Б–ї—Г—З–∞—П –≤—Б—К—Й–љ–Њ—Б—В –µ —Б–∞–Љ–Њ –≥—А–∞—Д) –Є –і–∞ —Б–µ —В—А–∞–љ—Б—Д–Њ—А–Љ–Є—А–∞—В –≤ —З–µ—В–Є—А–Є –љ–Њ–≤–Є –≤—А—К–Ј–Ї–Є, —Б—К–Ј–і–∞–≤–∞–є–Ї–Є –љ–Њ–≤ –µ–ї–µ–Љ–µ–љ—В –≤ –њ—А–Њ—Ж–µ—Б–∞. –Ґ–∞–Ї–∞ —З–µ –≤—Б—П–Ї–∞ вАЮ—Б—В—К–њ–Ї–∞вАЬ, –Ї–Њ—П—В–Њ –±–µ –њ–Њ–Ї–∞–Ј–∞–љ–∞ –њ—А–µ–і–Є, –≤—Б—К—Й–љ–Њ—Б—В —Б–µ —Б—К—Б—В–Њ–Є –Њ—В –љ—П–Ї–Њ–ї–Ї–Њ –Њ—В–і–µ–ї–љ–Є вАЮ–∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞—Й–Є —Б—К–±–Є—В–Є—ПвАЬ (—В—Г–Ї —Б–∞ –њ–Њ–і—З–µ—А—В–∞–љ–Є –љ–Њ–≤–Њ –і–Њ–±–∞–≤–µ–љ–Є—В–µ –≤—А—К–Ј–Ї–Є –Є —В–µ–Ј–Є, –Ї–Њ–Є—В–Њ –њ—А–µ–і—Б—В–Њ–Є –і–∞ –±—К–і–∞—В –њ—А–µ–Љ–∞—Е–љ–∞—В–Є).

–Э–Њ —Б–µ–≥–∞ —В—Г–Ї –µ —А–µ—И–∞–≤–∞—Й–Є—П—В –Љ–Њ–Љ–µ–љ—В: —В–Њ–≤–∞ –љ–µ –µ –µ–і–Є–љ—Б—В–≤–µ–љ–∞—В–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В –љ–∞ –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞–љ–µ –љ–∞ —Б—К–±–Є—В–Є—П—В–∞, —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞—Й–Є –љ–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ. –Я—А–∞–≤–Є–ї–Њ—В–Њ –њ—А–Њ—Б—В–Њ –Ї–∞–Ј–≤–∞ –і–∞ —Б–µ –љ–∞–Љ–µ—А—П—В –і–≤–µ —Б—К—Б–µ–і–љ–Є –≤—А—К–Ј–Ї–Є –Є –∞–Ї–Њ –Є–Љ–∞ –љ—П–Ї–Њ–ї–Ї–Њ –≤—К–Ј–Љ–Њ–ґ–љ–Є –Є–Ј–±–Њ—А–∞, –љ–µ –Ї–∞–Ј–≤–∞ –љ–Є—Й–Њ –Ї–Њ–Є –≤—А—К–Ј–Ї–Є —В—А—П–±–≤–∞ –і–∞ —Б–µ –Є–Ј–±–µ—А–∞—В. –Ш –µ–і–љ–∞ –Ї–ї—О—З–Њ–≤–∞ –Є–і–µ—П –≤ –Љ–Њ–і–µ–ї–∞ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –≤ –Є–Ј–≤–µ—Б—В–µ–љ —Б–Љ–Є—Б—К–ї¬†–њ—А–Њ—Б—В–Њ –і–∞ –њ–Њ–Ї–∞–ґ–µ —В–µ–Ј–Є –Є–Ј–±–Њ—А–Є.
–Ґ–Њ–≤–∞ –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–і—Б—В–∞–≤–Є —Б –≥—А–∞—Д, –Ї–Њ–є—В–Њ –њ–Њ–Ї–∞–Ј–≤–∞ –≤—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—К—В–Є—Й–∞:

–Ч–∞ –њ—К—А–≤–∞—В–∞ –∞–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є—П –Є–Љ–∞ –і–≤–µ –≤—К–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є. –Ґ–Њ–≥–∞–≤–∞ –Ј–∞ –≤—Б–µ–Ї–Є –Њ—В —А–µ–Ј—Г–ї—В–∞—В–Є—В–µ –Њ—В —В—П—Е –Є–Љ–∞ —З–µ—В–Є—А–Є –і–Њ–њ—К–ї–љ–Є—В–µ–ї–љ–Є –≤—К–Ј–Љ–Њ–ґ–љ–Њ—Б—В–Є. –Э–Њ –њ—А–Є —Б–ї–µ–і–≤–∞—Й–∞—В–∞ –∞–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є—П —Б–µ —Б–ї—Г—З–≤–∞ –љ–µ—Й–Њ –≤–∞–ґ–љ–Њ: –і–≤–∞ –Њ—В –Ї–ї–Њ–љ–Њ–≤–µ—В–µ —Б–µ —Б–ї–Є–≤–∞—В. –° –і—А—Г–≥–Є –і—Г–Љ–Є, –≤—К–њ—А–µ–Ї–Є —А–∞–Ј–ї–Є—З–љ–∞—В–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В –љ–∞ –∞–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є–Є—В–µ, —А–µ–Ј—Г–ї—В–∞—В—К—В –µ –µ–і–Є—В –Є —Б—К—Й.
–Э–µ—Й–∞—В–∞ –±—К—А–Ј–Њ —Б–µ —Г—Б–ї–Њ–ґ–љ—П–≤–∞—В. –Х—В–Њ –≥—А–∞—Д—К—В —Б–ї–µ–і –Њ—Й–µ –µ–і–љ–∞ –∞–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є—П, –Ї–Њ—П—В–Њ –≤–µ—З–µ –љ–µ¬† –њ–Њ–Ї–∞–Ј–≤–∞ —А–∞–Ј–≤–Є—В–Є–µ—В–Њ –Љ—Г –љ–∞–і–Њ–ї—Г –≤ —Б—В—А–∞–љ–Є—Ж–∞—В–∞:

–Ш —В–∞–Ї–∞, –Ї–∞–Ї —Б–µ —Б–≤—К—А–Ј–≤–∞ —Б –≤—А–µ–Љ–µ—В–Њ? –Э—П–Љ–∞ —Б–∞–Љ–Њ –µ–і–Є–љ –њ—К—В –љ–∞ –≤—А–µ–Љ–µ—В–Њ, –Є–Љ–∞ –Љ–љ–Њ–≥–Њ –њ—К—В–µ–Ї–Є –Є –Љ–љ–Њ–≥–Њ вАЮ–Є—Б—В–Њ—А–Є–ЄвАЬ. –Э–Њ –Љ–Њ–і–µ–ї—К—В - –Є –њ—А–∞–≤–Є–ї–Њ—В–Њ, –Ї–Њ–µ—В–Њ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞ - –Њ–њ—А–µ–і–µ–ї—П –≤—Б–Є—З–Ї–Є —В—П—Е. –Ш –≤–Є–і—П—Е–Љ–µ –љ–∞–Љ–µ–Ї –Ј–∞ –љ–µ—Й–Њ –і—А—Г–≥–Њ: —З–µ –і–Њ—А–Є –Є –і–∞ –Љ–Є—Б–ї–Є–Љ, —З–µ —Б–ї–µ–і–≤–∞–Љ–µ вАЮ–љ–µ–Ј–∞–≤–Є—Б–Є–ЉвАЬ –њ—К—В –љ–∞ –Є—Б—В–Њ—А–Є—П—В–∞, —В–Њ–є –≤—Б—К—Й–љ–Њ—Б—В –Љ–Њ–ґ–µ –і–∞ —Б–µ —Б–ї–µ–µ —Б –і—А—Г–≥ –њ—К—В.
–У—А–∞—Д—К—В –љ–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—А—К–Ј–Ї–Є
–Ф–∞ –Ї–∞–ґ–µ–Љ, —З–µ –Є–Љ–∞–Љ–µ –њ—А–∞–≤–Є–ї–Њ—В–Њ:
{A вЖТ BBB, BB вЖТ A}
–Я—А–∞–≤–Є–ї–Њ—В–Њ –µ: –Ї—К–і–µ—В–Њ –Є –і–∞ —Б—А–µ—Й–љ–µ–Љ¬†–Р, –Љ–Њ–ґ–µ–Љ –і–∞ –≥–Њ –Ј–∞–Љ–µ–љ–Є–Љ —Б BBB –Є –љ–∞–≤—Б—П–Ї—К–і–µ, –Ї—К–і–µ—В–Њ —Б—А–µ—Й–љ–µ–Љ BB, –Љ–Њ–ґ–µ–Љ –і–∞ –≥–Є –Ј–∞–Љ–µ–љ–Є —Б A. –Р–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є–Є—В–µ –љ–∞ AB –Є BA –і–∞–≤–∞—В BBBB. –°–ї–µ–і —В–Њ–≤–∞ BBBB —Б—В–∞–≤–∞ ABB, BBA –Є BAB.¬†–° –≤—Б—П–Ї–Њ –њ—А–Є–ї–∞–≥–∞–љ–µ –љ–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ, –≥—А–∞—Д—К—В —Б–µ —Г—Б–ї–Њ–ґ–љ—П–≤–∞:
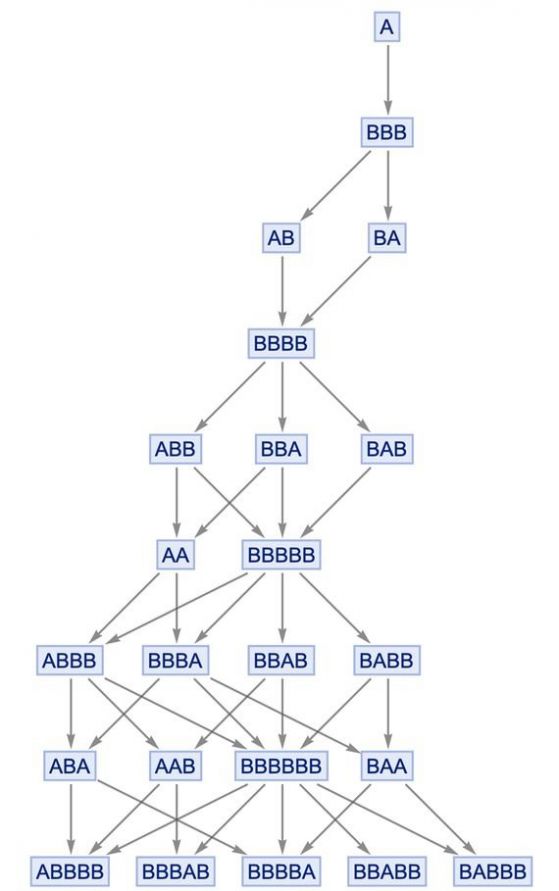
–Ш –∞–Ї–Њ –њ—А–Њ—Б–ї–µ–і–Є–Љ —Б—Е–µ–Љ–∞—В–∞ –њ–Њ-–≥–Њ—А–µ, —Й–µ¬†–≤–Є–і–Є–Љ, —З–µ –≤—Б—П–Ї–∞¬†–і–≤–Њ–є–Ї–∞ —А–∞–Ј–Ї–ї–Њ–љ–µ–љ–Є—П –≤–Є–љ–∞–≥–Є —Б–µ —Б–ї–Є–≤–∞, –∞ –≤ —В–Њ–Ј–Є —Б–ї—Г—З–∞–є —Б–∞–Љ–Њ —Б–ї–µ–і –Њ—Й–µ –µ–і–љ–∞ —Б—В—К–њ–Ї–∞.
–Ґ–Њ–Ј–Є –≤–Є–і –±–∞–ї–∞–љ—Б –Љ–µ–ґ–і—Г —А–∞–Ј–Ї–ї–Њ–љ—П–≤–∞–љ–µ –Є —Б–ї–Є–≤–∞–љ–µ –µ —П–≤–ї–µ–љ–Є–µ, –Ї–Њ–µ—В–Њ –Т–Њ–ї—Д—А–∞–Љ –љ–∞—А–Є—З–∞ вАЮ–њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—ВвАЬ. –Ш –Љ–∞–Ї–∞—А —З–µ —В—Г–Ї –Љ–Њ–ґ–µ –і–∞ –Є–Ј–≥–ї–µ–ґ–і–∞ –Ї–∞—В–Њ –њ—А–Њ—Б—В–Њ –љ—П–Ї–∞–Ї–≤–∞ –њ–Њ–і—А–Њ–±–љ–Њ—Б—В, —В–∞–Ї–Є–≤–∞ –Ї–Њ–љ–≤–µ—А–≥–µ–љ—Ж–Є–Є –њ–Њ–Ј–≤–Њ–ї—П–≤–∞—В –і–∞ —Б–µ –Ј–∞–њ–∞–Ј–Є –њ—А–Є—З–Є–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞—В–∞ –≤–µ—А–Є–≥–∞¬†–љ–∞ —Б—К–±–Є—В–Є—П—В–∞¬†–≤—К–≤ –≤—А–µ–Љ–µ—В–Њ.¬†
–Ф–Њ—А–Є –Ї–Њ–≥–∞—В–Њ –њ—К—В–Є—Й–∞—В–∞ –љ–∞ –Є—Б—В–Њ—А–Є—П—В–∞, –Ї–Њ–Є—В–Њ —Б–µ —Б–ї–µ–і–≤–∞—В, —Б–∞ —А–∞–Ј–ї–Є—З–љ–Є, —В–µ–Ј–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –≤—А—К–Ј–Ї–Є –Љ–Њ–≥–∞—В –і–∞ —Б–µ –Њ–Ї–∞–ґ–∞—В –µ–і–љ–∞–Ї–≤–Є - –Є –≤ –і–µ–є—Б—В–≤–Є—В–µ–ї–љ–Њ—Б—В –Ј–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї, –≤–≥—А–∞–і–µ–љ –≤ —Б–Є—Б—В–µ–Љ–∞—В–∞, —Й–µ –Є–Љ–∞ —Б–∞–Љ–Њ –µ–і–љ–∞ –ї–Є–љ–Є—П –љ–∞ –≤—А–µ–Љ–µ—В–Њ.
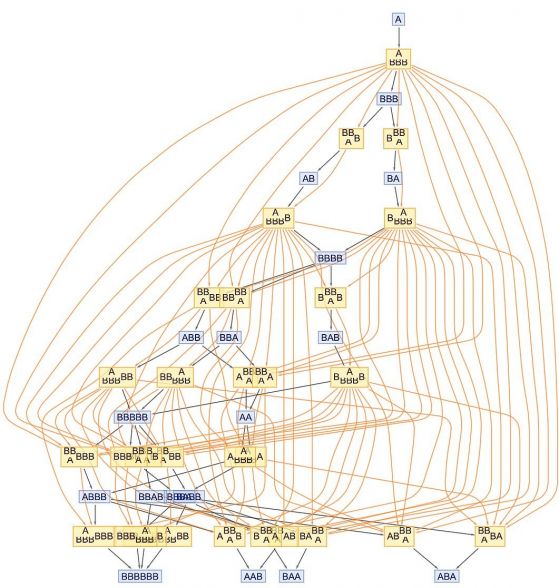 –Х—В–Њ –Ї–∞–Ї–≤–Њ —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞, –∞–Ї–Њ —Б–µ –њ–Њ–Ї–∞–ґ–∞—В –≤—Б–Є—З–Ї–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б—К–±–Є—В–Є—П—В–∞. –Ю—А–∞–љ–ґ–µ–≤–Є—В–µ –ї–Є–љ–Є–Є –њ–Њ–Ї–∞–Ј–≤–∞—В –Ї–Њ–µ —Б—К–±–Є—В–Є–µ —В—А—П–±–≤–∞ –і–∞ —Б–µ —Б–ї—Г—З–Є –њ—А–µ–і–Є –і—А—Г–≥–Њ —Б—К–±–Є—В–Є–µ –Є–ї–Є –Ї–∞–Ї–≤–Є —Б–∞ –≤—Б–Є—З–Ї–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –≤—А—К–Ј–Ї–Є —Б –≤—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—К—В–Є—Й–∞ –≤ –Љ—Г–ї—В–Є–≤–∞—А–Є–∞–љ—В–љ–∞—В–∞ —Б–Є—Б—В–µ–Љ–∞,¬†–Ї–∞–Ї—В–Њ –Є —Ж—П–ї–∞—В–∞ –Љ—А–µ–ґ–∞ –Њ—В –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –≤—А—К–Ј–Ї–Є –≤—К—В—А–µ –Є –Љ–µ–ґ–і—Г —В–µ–Ј–Є –њ—К—В–µ–Ї–Є.
–Х—В–Њ –Ї–∞–Ї–≤–Њ —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞, –∞–Ї–Њ —Б–µ –њ–Њ–Ї–∞–ґ–∞—В –≤—Б–Є—З–Ї–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Љ–µ–ґ–і—Г —Б—К–±–Є—В–Є—П—В–∞. –Ю—А–∞–љ–ґ–µ–≤–Є—В–µ –ї–Є–љ–Є–Є –њ–Њ–Ї–∞–Ј–≤–∞—В –Ї–Њ–µ —Б—К–±–Є—В–Є–µ —В—А—П–±–≤–∞ –і–∞ —Б–µ —Б–ї—Г—З–Є –њ—А–µ–і–Є –і—А—Г–≥–Њ —Б—К–±–Є—В–Є–µ –Є–ї–Є –Ї–∞–Ї–≤–Є —Б–∞ –≤—Б–Є—З–Ї–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –≤—А—К–Ј–Ї–Є —Б –≤—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—К—В–Є—Й–∞ –≤ –Љ—Г–ї—В–Є–≤–∞—А–Є–∞–љ—В–љ–∞—В–∞ —Б–Є—Б—В–µ–Љ–∞,¬†–Ї–∞–Ї—В–Њ –Є —Ж—П–ї–∞—В–∞ –Љ—А–µ–ґ–∞ –Њ—В –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –≤—А—К–Ј–Ї–Є –≤—К—В—А–µ –Є –Љ–µ–ґ–і—Г —В–µ–Ј–Є –њ—К—В–µ–Ї–Є.
–Я—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞—В–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В –њ—А–µ–і–њ–Њ–ї–∞–≥–∞, —З–µ –≤—Б—К—Й–љ–Њ—Б—В –≥—А–∞—Д—К—В –љ–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—А—К–Ј–Ї–Є –µ –µ–і–Є–љ –Є —Б—К—Й, –љ–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ –Ї–Њ–є –њ—К—В –љ–∞ –Є—Б—В–Њ—А–Є—П—В–∞ —Б–µ —Б–ї–µ–і–≤–∞.
–Ш –∞–Ї–Њ —Б–µ –њ—А–Њ—Б–ї–µ–і–Є —Б—Е–µ–Љ–∞—В–∞ –њ–Њ-–≥–Њ—А–µ (–Є —Б–µ –Є–Ј–≤—К—А–≤—П—В –Њ—Й–µ –љ—П–Ї–Њ–ї–Ї–Њ —Б—В—К–њ–Ї–Є), —Й–µ —Б–µ –Њ—В–Ї—А–Є–µ, —З–µ –Ј–∞ –≤—Б–µ–Ї–Є –њ—К—В –љ–∞ –Є—Б—В–Њ—А–Є—П—В–∞ –Ї–∞–Ј—Г–∞–ї–љ–Є—П—В –≥—А–∞—Д, –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞—Й –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—А—К–Ј–Ї–Є –Љ–µ–ґ–і—Г —Б—К–±–Є—В–Є—П—В–∞, –≤–Є–љ–∞–≥–Є —Й–µ –±—К–і–µ –Њ—В —В–Њ–Ј–Є –≤–Є–і:
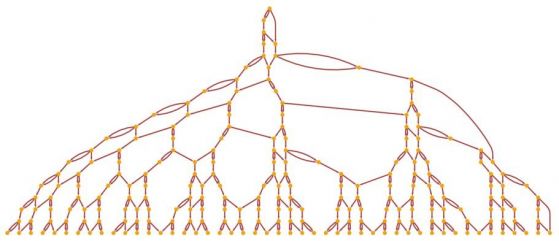
–С–ї–∞–≥–Њ–і–∞—А–µ–љ–Є–µ –љ–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞—В–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В, —Е–Є–њ–µ—А–≥—А–∞—Д–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –≤—К–Ј–њ—А–Њ–Є–Ј–≤–µ–ґ–і–∞—В –Љ–љ–Њ–≥–Њ –Њ—В —Б–ї–µ–і—Б—В–≤–Є—П—В–∞ –љ–∞ —А–∞–Ј–ї–Є—З–љ–Є —Д–Є–Ј–Є—З–µ—Б–Ї–Є —В–µ–Њ—А–Є–Є, –Ї–∞—В–Њ –°–њ–µ—Ж–Є–∞–ї–љ–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ.
–Ґ—К–є –Ї–∞—В–Њ –Є–Љ–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В, –љ–Є–µ –Ј–љ–∞–µ–Љ –љ–µ—Й–Њ –Љ–љ–Њ–≥–Њ –≤–∞–ґ–љ–Њ: —В–Њ–≤–∞ —Б–∞ –≤—Б—К—Й–љ–Њ—Б—В –Љ–љ–Њ–≥–Њ –Ї–Њ–њ–Є—П –љ–∞ –µ–і–Є–љ –Є —Б—К—Й –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ –≥—А–∞—Д - –њ—А–Њ—Б—В–∞ —А–µ—И–µ—В–Ї–∞:

–Ъ—А—К—Б—В–Њ—Б–∞–љ–Є—В–µ –≤—А—К–Ј–Ї–Є –Љ–µ–ґ–і—Г —В–µ–Ј–Є –Ї–Њ–њ–Є—П –љ–µ —Б–∞ —В—А–Є–≤–Є–∞–ї–љ–Є, –∞ —Б–∞ —Б–≤—К—А–Ј–∞–љ–Є —Б –і—К–ї–±–Њ–Ї–Є –≤—А—К–Ј–Ї–Є –Љ–µ–ґ–і—Г —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ –Є –Ї–≤–∞–љ—В–Њ–≤–∞—В–∞ –Љ–µ—Е–∞–љ–Є–Ї–∞.
–Т—Б–µ–Ї–Є —А–∞–Ј–ї–Є—З–µ–љ –љ–∞—З–Є–љ –љ–∞ –њ—А–Є–ї–∞–≥–∞–љ–µ –љ–∞ –њ—А–∞–≤–Є–ї–Њ—В–Њ –Ј–∞ —Б–Њ—А—В–Є—А–∞–љ–µ —В—А—П–±–≤–∞ –і–∞ –і–∞–≤–∞ –µ–і–Є–љ –Є —Б—К—Й –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ –≥—А–∞—Д. –Х—В–Њ –µ–і–Є–љ –њ—А–Є–Љ–µ—А –Ј–∞ —В–Њ–≤–∞ –Ї–∞–Ї –Љ–Њ–ґ–µ–Љ –і–∞ –њ—А–Є–ї–Њ–ґ–Є–Љ –њ—А–∞–≤–Є–ї–Њ—В–Њ, –Ј–∞–њ–Њ—З–≤–∞–є–Ї–Є —Б –Њ–њ—А–µ–і–µ–ї–µ–љ –љ–∞—З–∞–ї–µ–љ –љ–Є–Ј:

–Э–Њ —Б–µ–≥–∞ –љ–µ–Ї–∞ –њ–Њ–Ї–∞–ґ–µ–Љ –≥—А–∞—Д—К—В –љ–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—А—К–Ј–Ї–Є. –Ш –≤–Є–ґ–і–∞–Љ–µ, —З–µ —В–Њ–≤–∞ –µ –њ—А–Њ—Б—В–Њ —А–µ—И–µ—В–Ї–∞:

–Х—В–Њ —В—А–Є –і—А—Г–≥–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В–Є –љ–∞ –∞–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є–Є—В–µ:

–°–µ–≥–∞ –≤–Є–ґ–і–∞–Љ–µ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞—В–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В –≤ –і–µ–є—Б—В–≤–Є–µ: –≤—К–њ—А–µ–Ї–Є —З–µ –≤ —А–∞–Ј–ї–Є—З–љ–Є –Љ–Њ–Љ–µ–љ—В–Є —Б–µ —Б–ї—Г—З–≤–∞—В —А–∞–Ј–ї–Є—З–љ–Є –∞–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є–Є, –≥—А–∞—Д—К—В –љ–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—А—К–Ј–Ї–Є –Љ–µ–ґ–і—Г —Б—К–±–Є—В–Є—П—В–∞ –≤–Є–љ–∞–≥–Є –µ –µ–і–Є–љ –Є —Б—К—Й–Є.¬†
–Ш–Ј–≤–ї–Є—З–∞–љ–µ –љ–∞¬†–°–њ–µ—Ж–Є–∞–ї–љ–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞
–Ґ–Є–њ–Є—З–µ–љ –њ—К—А–≤–Є –Є–љ—Б—В–Є–љ–Ї—В –≤ –Љ–Є—Б–ї–µ–љ–µ—В–Њ –љ–∞ –Ј–∞–љ–Є–Љ–∞–≤–∞—Й–Є—В–µ —Б–µ —Б –љ–∞—Г–Ї–∞ –µ –і–∞ —Б–Є –њ—А–µ–і—Б—В–∞–≤—П—В –Ї–∞–Ї –њ—А–∞–≤—П—В –µ–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В –≤—К—А—Е—Г —Б–Є—Б—В–µ–Љ–∞, –љ–Њ –Ї–∞—В–Њ вАЮ–љ–∞–±–ї—О–і–∞—В–µ–ї–ЄвАЬ –Є–Ј–≤—К–љ —Б–Є—Б—В–µ–Љ–∞—В–∞. –Э–Њ –∞–Ї–Њ —В—А—П–±–≤–∞ –і–∞ —Б–µ –Љ–Њ–і–µ–ї–Є—А–∞—В —Ж—П–ї–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞ –Є –≤—Б–Є—З–Ї–Њ –≤ –љ–µ—П, —В–Њ–≤–∞ –≤ –Ї—А–∞–є–љ–∞ —Б–Љ–µ—В–Ї–∞ –љ–µ –µ —А–∞–Ј—Г–Љ–µ–љ –љ–∞—З–Є–љ, –Ј–∞—Й–Њ—В–Њ вАЮ–љ–∞–±–ї—О–і–∞—В–µ–ї—П—ВвАЬ –љ–µ–Љ–Є–љ—Г–µ–Љ–Њ –µ —З–∞—Б—В –Њ—В –Т—Б–µ–ї–µ–љ–∞—В–∞ –Є –Ј–∞—В–Њ–≤–∞ —В—А—П–±–≤–∞ –і–∞ —Б–µ –Љ–Њ–і–µ–ї–Є—А–∞ –Ї–∞–Ї—В–Њ –≤—Б–Є—З–Ї–Њ –Њ—Б—В–∞–љ–∞–ї–Њ.
–Т –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ —В–Њ–≤–∞ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ вАЮ—Г–Љ—К—В –љ–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї—ПвАЬ, –њ–Њ–і–Њ–±–љ–Њ –љ–∞ –≤—Б–Є—З–Ї–Њ –Њ—Б—В–∞–љ–∞–ї–Њ –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞, —В—А—П–±–≤–∞ –і–∞ —Б–µ –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞ —З—А–µ–Ј –њ–Њ—А–µ–і–Є—Ж–∞ –Њ—В –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞—Й–Є —Б—К–±–Є—В–Є—П. –Э—П–Љ–∞ –∞–±—Б–Њ–ї—О—В–µ–љ –љ–∞—З–Є–љ –љ–∞–±–ї—О–і–∞—В–µ–ї—П—В –і–∞ вАЮ–Ј–љ–∞–µ –Ї–∞–Ї–≤–Њ —Б–µ —Б–ї—Г—З–≤–∞ –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞вАЬ, –≤—Б–Є—З–Ї–Њ, –Ї–Њ–µ—В–Њ –њ—А–µ–ґ–Є–≤—П–≤–∞ —В–Њ–є, –µ –њ–Њ—А–µ–і–Є—Ж–∞ –Њ—В –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞—Й–Є —Б—К–±–Є—В–Є—П, –Ї–Њ–Є—В–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –Ј–∞—Б–µ–≥–љ–∞—В–Є –Њ—В –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞–љ–µ—В–Њ –љ–∞ —Б—К–±–Є—В–Є—П—В–∞, —Б–ї—Г—З–≤–∞—Й–Є —Б–µ –і—А—Г–≥–∞–і–µ –≤—К–≤ –Т—Б–µ–ї–µ–љ–∞—В–∞. –Ш–ї–Є –Ї–∞–Ј–∞–љ–Њ –њ–Њ —А–∞–Ј–ї–Є—З–µ–љ –љ–∞—З–Є–љ, –≤—Б–Є—З–Ї–Њ, –Ї–Њ–µ—В–Њ –љ–∞–±–ї—О–і–∞—В–µ–ї—П—В –Љ–Њ–ґ–µ –і–∞ –љ–∞–±–ї—О–і–∞–≤–∞, –µ –Љ—А–µ–ґ–∞—В–∞ –Њ—В –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є –≤—А—К–Ј–Ї–Є –Љ–µ–ґ–і—Г —Б—К–±–Є—В–Є—П—В–∞ - –Є–ї–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—П –≥—А–∞—Д.
–°–µ–≥–∞ –љ–µ–Ї–∞ –њ–Њ–Љ–Є—Б–ї–Є–Љ –Ї–∞–Ї –љ–∞–±–ї—О–і–∞—В–µ–ї–Є—В–µ –Љ–Њ–≥–∞—В –і–∞ вАЮ–њ—А–µ–ґ–Є–≤–µ—П—ВвАЬ —В–Њ–Ј–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ –≥—А–∞—Д. –Ю—В–і–Њ–ї—Г –љ–∞–±–ї—О–і–∞—В–µ–ї—П—В —Б–µ –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞ —З—А–µ–Ј –љ—П–Ї–∞–Ї–≤–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В –Њ—В –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞–љ–µ –љ–∞ —Б—К–±–Є—В–Є—П—В–∞. –Э–Њ –≤—К–њ—А–µ–Ї–Є —З–µ —В–Њ–≤–∞ вАЮ–љ–∞–Є—Б—В–Є–љ–∞ —Б–µ —Б–ї—Г—З–≤–∞вАЬ, –Ј–∞ –і–∞ –≥–Њ –Њ—Б–Љ–Є—Б–ї–Є–Љ, –Љ–Њ–ґ–µ–Љ –і–∞ —Б–Є –њ—А–µ–і—Б—В–∞–≤–Є–Љ –Ї–∞–Ї –љ–∞—И–Є—В–µ –љ–∞–±–ї—О–і–∞—В–µ–ї–Є —Б—К–Ј–і–∞–≤–∞—В –≤—К—В—А–µ—И–љ–Є вАЮ–Љ–µ–љ—В–∞–ї–љ–ЄвАЬ –Љ–Њ–і–µ–ї–Є –Ј–∞ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –≤–Є–ґ–і–∞—В. –Ш –і–Њ—Б—В–∞ –µ—Б—В–µ—Б—В–≤–µ–љ–Њ –љ–µ—Й–Њ –Ј–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї–Є—В–µ –Ї–∞—В–Њ –љ–∞—Б –µ –њ—А–Њ—Б—В–Њ –і–∞ –Ї–∞–ґ–∞—В вАЮ–µ–і–Є–љ –Ї–Њ–Љ–њ–ї–µ–Ї—В –љ–µ—Й–∞ —Б–µ —Б–ї—Г—З–≤–∞ –≤ —Ж—П–ї–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞, —Б–ї–µ–і —В–Њ–≤–∞ –і—А—Г–≥ –Є —В.–љ.вАЬ. –Ш –Љ–Њ–ґ–µ–Љ –і–∞ –≥–Њ –њ—А–µ–≤–µ–і–µ–Љ –Ї–∞—В–Њ –Ї–∞–Ј–≤–∞–Љ–µ, —З–µ —Б–Є –њ—А–µ–і—Б—В–∞–≤—П–Љ–µ –њ–Њ—А–µ–і–Є—Ж–∞ –Њ—В вАЮ–Љ–Њ–Љ–µ–љ—В–ЄвАЬ –≤—К–≤ –≤—А–µ–Љ–µ—В–Њ, –Ї—К–і–µ—В–Њ –љ–µ—Й–∞—В–∞ —Б–µ —Б–ї—Г—З–≤–∞—В вАЮ–µ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–ЊвАЬ –≤ —Ж—П–ї–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞ - –њ–Њ–љ–µ —Б –љ—П–Ї–∞–Ї–≤–∞ –Ї–Њ–љ–≤–µ–љ—Ж–Є—П –Ј–∞ –µ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ—Б—В.
–Х—В–Њ –µ–і–Є–љ –≤—К–Ј–Љ–Њ–ґ–µ–љ –љ–∞—З–Є–љ –Ј–∞ —В–Њ–≤–∞:

–І–Њ–≤–µ–Ї –Љ–Њ–ґ–µ –і–∞ –Њ–њ–Є—И–µ —В–Њ–≤–∞ –Ї–∞—В–Њ вАЮ—Б–ї–Њ–µ–≤–µвАЬ –љ–∞ –Ї–∞–Ј—Г–∞–ї–љ–Є—П –≥—А–∞—Д. –†–∞–Ј–і–µ–ї—П–Љ–µ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—П –≥—А–∞—Д –љ–∞ —Б–ї–Њ–µ–≤–µ –Є–ї–Є —А–µ–Ј–µ–љ–Є. –Ш –≤—Б–µ–Ї–Є —Б–ї–Њ–є –љ–∞–±–ї—О–і–∞—В–µ–ї–Є—В–µ –Љ–Њ–≥–∞—В –і–∞ —Б—З–Є—В–∞—В –Ј–∞ вАЮ–њ–Њ—А–µ–і–µ–љ –Љ–Њ–Љ–µ–љ—В –≤—К–≤ –≤—А–µ–Љ–µ—В–ЊвАЬ.
–Т–∞–ґ–љ–Њ –µ –і–∞ —Б–µ –Њ—В–±–µ–ї–µ–ґ–Є, —З–µ –Є–Љ–∞ –љ—П–Ї–Њ–Є –Њ–≥—А–∞–љ–Є—З–µ–љ–Є—П –≤—К–≤ —Д–Њ–ї–Є–∞—Ж–Є—П—В–∞ (—А–∞–Ј–і–µ–ї—П–љ–µ—В–Њ –љ–∞ —Б–ї–Њ–µ–≤–µ), –Ї–Њ—П—В–Њ –Љ–Њ–ґ–µ–Љ –і–∞ –Є–Ј–±–µ—А–µ–Љ. –Я—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—П—В –≥—А–∞—Д –Њ–њ—А–µ–і–µ–ї—П –Ї–∞–Ї–≤–Њ —Б—К–±–Є—В–Є–µ —В—А—П–±–≤–∞ –і–∞ —Б–µ —Б–ї—Г—З–Є, –Ј–∞ –і–∞ —Б–µ —Б–ї—Г—З–Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Њ —Б–ї–µ–і–≤–∞—Й–Њ. –Ш –∞–Ї–Њ –љ–∞–±–ї—О–і–∞—В–µ–ї–Є—В–µ —Й–µ –Є–Љ–∞—В —И–∞–љ—Б–∞ –і–∞ –Њ—Б–Љ–Є—Б–ї—П—В —Б–≤–µ—В–∞, –њ–Њ-–і–Њ–±—А–µ –µ¬† –њ—А–µ–і—Б—В–∞–≤–∞—В–∞ –Є–Љ –Ј–∞ –љ–∞–њ—А–µ–і—К–Ї–∞ –љ–∞ –≤—А–µ–Љ–µ—В–Њ –і–∞ —Б–µ –њ—А–Є–≤–µ–і–µ –≤ —Б—К–Њ—В–≤–µ—В—Б—В–≤–Є–µ —Б —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –Ї–∞–Ј–≤–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—П—В –≥—А–∞—Д. –Ґ–∞–Ї–∞ –љ–∞–њ—А–Є–Љ–µ—А, —В–Њ–≤–∞ —А–∞–Ј–і–µ–ї—П–љ–µ –љ–∞ —Б–ї–Њ–µ–≤–µ –љ–µ –±–Є —А–∞–±–Њ—В–Є–ї–Њ - –Ј–∞—Й–Њ—В–Њ –њ–Њ–Ї–∞–Ј–≤–∞, —З–µ –≤—А–µ–Љ–µ—В–Њ, –Њ—В—А–µ–ґ–і–∞–љ–Њ –љ–∞ —Б—К–±–Є—В–Є—П—В–∞, —Й–µ —Б–µ —А–∞–Ј–Љ–Є–љ–∞–≤–∞ —Б —А–µ–і–∞, –≤ –Ї–Њ–є—В–Њ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—П—В –≥—А–∞—Д –Њ–њ—А–µ–і–µ–ї—П, —З–µ —В—А—П–±–≤–∞ –і–∞ —Б–µ —Б–ї—Г—З–∞—В:

–Р–Ї–Њ —Б–≤—К—А–ґ–µ–Љ —В–Њ–≤–∞ —Б —Д–Є–Ј–Є–Ї–∞—В–∞, —Д–Њ–ї–Є–∞—Ж–Є—П—В–∞ –µ –Њ—В –Ј–љ–∞—З–µ–љ–Є–µ –Ј–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї–Є, –Ї–Њ–Є—В–Њ –њ–Њ –љ—П–Ї–∞–Ї—К–≤ –љ–∞—З–Є–љ —Б–∞ вАЮ–љ–µ–њ–Њ–і–≤–Є–ґ–љ–Є –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞вАЬ (вАЮ–Ї–Њ—Б–Љ–Њ–ї–Њ–≥–Є—З–љ–∞ —А–∞–Љ–Ї–∞ –љ–∞ –њ–Њ–Ї–Њ–євАЬ). –І–Њ–≤–µ–Ї –Љ–Њ–ґ–µ –і–∞ —Б–Є –њ—А–µ–і—Б—В–∞–≤–Є, —З–µ —Б —В–µ—З–µ–љ–Є–µ –љ–∞ –≤—А–µ–Љ–µ—В–Њ —Б—К–±–Є—В–Є—П—В–∞, –Ї–Њ–Є—В–Њ –њ—А–µ–ґ–Є–≤—П–≤–∞ –Њ–њ—А–µ–і–µ–ї–µ–љ –љ–∞–±–ї—О–і–∞—В–µ–ї, —Б–∞ —В–µ–Ј–Є –≤ –Ї–Њ–ї–Њ–љ–∞—В–∞, –Ї–Њ—П—В–Њ –≤—К—А–≤–Є –≤–µ—А—В–Є–Ї–∞–ї–љ–Њ –љ–∞–і–Њ–ї—Г –њ–Њ —Б—В—А–∞–љ–Є—Ж–∞—В–∞:

–Э–Њ —Б–µ–≥–∞ –љ–µ–Ї–∞ –і–∞ —Б–Є –њ—А–µ–і—Б—В–∞–≤–Є–Љ –Ј–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї, –Ї–Њ–є—В–Њ —А–∞–≤–љ–Њ–Љ–µ—А–љ–Њ —Б–µ –і–≤–Є–ґ–Є –≤ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ. –Ґ–Њ–є —Й–µ –њ—А–µ–ґ–Є–≤–µ–µ —А–∞–Ј–ї–Є—З–љ–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В –Њ—В —Б—К–±–Є—В–Є—П, –і–∞ —А–µ—З–µ–Љ:

–Р —В–Њ–≤–∞ –Њ–Ј–љ–∞—З–∞–≤–∞, —З–µ —Д–Њ–ї–Є–∞—Ж–Є—П—В–∞, –Ї–Њ—П—В–Њ —В–Њ–є –µ—Б—В–µ—Б—В–≤–µ–љ–Њ —Й–µ –Ї–Њ–љ—Б—В—А—Г–Є—А–∞, —Й–µ –±—К–і–µ —А–∞–Ј–ї–Є—З–љ–∞. –Ю—В–≤—К–љ –Љ–Њ–ґ–µ –і–∞ —Б–µ –љ–∞—А–Є—Б—Г–≤–∞¬†–Ї–∞–Ј—Г–∞–ї–љ–Є—П –≥—А–∞—Д —В–∞–Ї–∞:

–Э–Њ –Ј–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї—П –≤—Б–µ–Ї–Є —Б–ї–Њ–є –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞ –њ—А–Њ—Б—В–Њ –њ–Њ—А–µ–і–µ–љ –Љ–Њ–Љ–µ–љ—В –Њ—В –≤—А–µ–Љ–µ. –Ш –љ—П–Љ–∞—В –љ–∞—З–Є–љ –і–∞ —А–∞–Ј–±–µ—А–µ –Ї–∞–Ї –µ –љ–∞—А–Є—Б—Г–≤–∞–љ –Ї–∞–Ј—Г–∞–ї–љ–Є—П –≥—А–∞—Д. –Ґ–∞–Ї–∞ —З–µ —В–Њ–є —Й–µ –Ї–Њ–љ—Б—В—А—Г–Є—А–∞ —Б–≤–Њ—П —Б–Њ–±—Б—В–≤–µ–љ–∞ –≤–µ—А—Б–Є—П, –Ї—К–і–µ—В–Њ —Б—А–µ–Ј–Њ–≤–µ—В–µ —Б–∞ —Е–Њ—А–Є–Ј–Њ–љ—В–∞–ї–љ–Є:

–Ч–∞ –і–∞ —Б–µ –Є–Ј–≤—К—А—И–Є —В–Њ–≤–∞ –њ—А–µ–љ–∞—А–µ–ґ–і–∞–љ–µ, –Ј–∞–њ–∞–Ј–≤–∞–є–Ї–Є –Њ—Б–љ–Њ–≤–љ–∞—В–∞ —Б—В—А—Г–Ї—В—Г—А–∞ (–Є —К–≥–ї–Є—В–µ) –љ–∞ –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—П –≥—А–∞—Д, –≤—Б–µ–Ї–Є –Љ–Њ–Љ–µ–љ—В –Њ—В –≤—А–µ–Љ–µ –Є–Ј–±–Є—А–∞ –њ–Њ-–Љ–∞–ї–Ї–Њ —Б—К–±–Є—В–Є—П –≤ –Ї–∞–Ј—Г–∞–ї–љ–Є—П –≥—А–∞—Д —Б –Ї–Њ–µ—Д–Є—Ж–Є–µ–љ—В, ![]() –Ї—К–і–µ—В–Њ ќ≤ –µ —К–≥—К–ї—К—В, –Ї–Њ–є—В–Њ –њ—А–µ–і—Б—В–∞–≤—П —Б–Ї–Њ—А–Њ—Б—В—В–∞ –љ–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї—П.
–Ї—К–і–µ—В–Њ ќ≤ –µ —К–≥—К–ї—К—В, –Ї–Њ–є—В–Њ –њ—А–µ–і—Б—В–∞–≤—П —Б–Ї–Њ—А–Њ—Б—В—В–∞ –љ–∞ –љ–∞–±–ї—О–і–∞—В–µ–ї—П.
–Э–Њ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –Т–Њ–ї—Д—А–∞–Љ –љ–∞—А–Є—З–∞ —Д–Њ–ї–Є–∞—Ж–Є–Є, –Ї–Њ–Є—В–Њ –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞—В –і–≤–Є–ґ–µ–љ–Є–µ—В–Њ, —Б–∞ —Б—В–∞–љ–і–∞—А—В–љ–Є—В–µ –∞ вАЮ–Њ—В–њ—А–∞–≤–љ–Є¬†–Є–љ–µ—А—Ж–Є–Њ–љ–љ–Є —Б–Є—Б—В–µ–Љ–ЄвАЬ –Њ—В –°–њ–µ—Ж–Є–∞–ї–љ–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞.
–Т–∞–ґ–µ–љ –Љ–Њ–Љ–µ–љ—В –µ, —З–µ –Ј–∞—А–∞–і–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞—В–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В –љ—П–Љ–∞ –Ј–љ–∞—З–µ–љ–Є–µ, —З–µ —Б–µ –љ–∞–Љ–Є—А–∞–Љ–µ –≤ –і—А—Г–≥–∞ –Њ—В–њ—А–∞–≤–љ–∞ –Є–љ–µ—А—Ж–Є–Њ–љ–љ–∞ —Б–Є—Б—В–µ–Љ–∞ - –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—П—В –≥—А–∞—Д –Ј–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ (–Є –љ–∞—З–Є–љ–∞, –њ–Њ –Ї–Њ–є—В–Њ –≤ –Ї—А–∞–є–љ–∞ —Б–Љ–µ—В–Ї–∞ —Б–µ –њ–Њ–і—А–µ–ґ–і–∞ –љ–Є–Ј—К—В) –µ –∞–±—Б–Њ–ї—О—В–љ–Њ –µ–і–Є–љ –Є —Б—К—Й–Є.
–Т –°–њ–µ—Ж–Є–∞–ї–љ–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞, –Њ—Б–љ–Њ–≤–љ–∞—В–∞ –Є–і–µ—П –µ, —З–µ "–Ј–∞–Ї–Њ–љ–Є—В–µ –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞" —А–∞–±–Њ—В—П—В –µ–і–љ–∞–Ї–≤–Њ –≤—К–≤ –≤—Б–Є—З–Ї–Є –Њ—В–њ—А–∞–≤–љ–Є –Є–љ–µ—А—Ж–Є–Њ–љ–љ–Є —Б–Є—Б—В–µ–Љ–Є.
–Э–Њ –Ј–∞—Й–Њ —В–Њ–≤–∞ —В—А—П–±–≤–∞ –і–∞ –µ –≤—П—А–љ–Њ?
–Ш –Т–Њ–ї—Д—А–∞–Љ –і–∞–≤–∞ –Њ—В–≥–Њ–≤–Њ—А: —В–Њ–≤–∞ –µ —Б–ї–µ–і—Б—В–≤–Є–µ –Њ—В –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞—В–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В –≤ –±–∞–Ј–Њ–≤–Є—В–µ –њ—А–∞–≤–Є–ї–∞. –° –і—А—Г–≥–Є –і—Г–Љ–Є, –Њ—В —Б–≤–Њ–є—Б—В–≤–Њ—В–Њ –љ–∞ –њ—А–Є—З–Є–љ–љ–∞—В–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В –Љ–Њ–ґ–µ–Љ –і–∞ –Є–Ј–≤–ї–µ—З–µ–Љ —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞.
–Ю–±–Є–Ї–љ–Њ–≤–µ–љ–Њ –≤—К–≤ —Д–Є–Ј–Є–Ї–∞—В–∞¬†—Б–µ –≤—К–≤–µ–ґ–і–∞¬†–Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В, –Ј–∞ –і–∞ —Б–µ —Б—К–Ј–і–∞–і–µ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞—В–∞ —Б—В—А—Г–Ї—В—Г—А–∞ –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ-–≤—А–µ–Љ–µ—В–Њ.
–Т–Њ–ї—Д—А–∞–Љ –љ–µ –њ—А–∞–≤–Є –љ–Є—Й–Њ –њ–Њ–і–Њ–±–љ–Њ –Є –≤—Б—К—Й–љ–Њ—Б—В –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є –≤—А–µ–Љ–µ—В–Њ –і–Њ—А–Є –љ–µ —Б–∞ –µ–і–љ–Њ –Є —Б—К—Й–Њ. –Э–Њ¬† –њ–Њ—А–∞–і–Є –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–∞—В–∞ –Є–љ–≤–∞—А–Є–∞–љ—В–љ–Њ—Б—В - –≤ –љ–µ–≥–Њ–≤–Є—В–µ –Љ–Њ–і–µ–ї–Є –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ —Б–µ –њ—А–Њ—П–≤—П–≤–∞ —Б –≤—Б–Є—З–Ї–Є –≤–Ј–∞–Є–Љ–Њ–Њ—В–љ–Њ—И–µ–љ–Є—П –Љ–µ–ґ–і—Г –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ –Є –≤—А–µ–Љ–µ, –Ї–Њ–Є—В–Њ —В–Њ–≤–∞ –Є–Ј–Є—Б–Ї–≤–∞ —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞.
–Ґ–∞–Ї–∞ –љ–∞–њ—А–Є–Љ–µ—А¬†–≤ –љ–µ–≥–Њ–≤–∞—В–∞ —Б–Є—Б—В–µ–Љ–∞ –Љ–Њ–ґ–µ–Љ –і–∞ —Б–µ –≤–Є–і–Є —А–µ–ї–∞—В–Є–≤–Є—Б—В–Ї–Њ –Ј–∞–±–∞–≤—П–љ–µ –љ–∞ –≤—А–µ–Љ–µ—В–Њ. –Т—Б—К—Й–љ–Њ—Б—В, –њ–Њ—А–∞–і–Є —Д–Њ–ї–Є–∞—Ж–Є—П—В–∞, –Ї–Њ—П—В–Њ –±–µ –Є–Ј–±—А–∞–љ–∞, –≤—А–µ–Љ–µ—В–Њ —А–∞–±–Њ—В–Є –њ–Њ-–±–∞–≤–љ–Њ. –Ш–ї–Є, –Ї–∞–Ј–∞–љ–Њ –њ–Њ –і—А—Г–≥ –љ–∞—З–Є–љ, –љ–∞–±–ї—О–і–∞—В–µ–ї—П—В –Є–Ј–њ–Є—В–≤–∞ –њ–Њ-–±–∞–≤–љ–Њ –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞–љ–µ –љ–∞ —Б–Є—Б—В–µ–Љ–∞—В–∞ –≤—К–≤ –≤—А–µ–Љ–µ—В–Њ.
–°–Ї–Њ—А–Њ—Б—В—В–∞ –љ–∞ —Б–≤–µ—В–ї–Є–љ–∞—В–∞ c –≤ —В–∞–Ј–Є —Б–Є—Б—В–µ–Љ–∞ —Б–µ –Њ–њ—А–µ–і–µ–ї—П –Њ—В –Љ–∞–Ї—Б–Є–Љ–∞–ї–љ–∞—В–∞ —Б–Ї–Њ—А–Њ—Б—В, —Б –Ї–Њ—П—В–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ —А–∞–Ј–њ—А–Њ—Б—В—А–∞–љ—П–≤–∞ –Є–љ—Д–Њ—А–Љ–∞—Ж–Є—П—В–∞, –Ї–Њ—П—В–Њ —Б–µ –Њ–њ—А–µ–і–µ–ї—П –Њ—В –њ—А–∞–≤–Є–ї–Њ—В–Њ, –∞ –≤ —Б–ї—Г—З–∞—П –љ–∞ —В–Њ–≤–∞ –њ—А–∞–≤–Є–ї–Њ –µ –µ–і–Є–љ –Ј–љ–∞–Ї –љ–∞ —Б—В—К–њ–Ї–∞. –Ш –њ–Њ –Њ—В–љ–Њ—И–µ–љ–Є–µ –љ–∞ —В–Њ–≤–∞ –Љ–Њ–ґ–µ–Љ —Б–ї–µ–і —В–Њ–≤–∞ –і–∞ –Ї–∞–ґ–µ–Љ, —З–µ –≤ —Б–ї—Г—З–∞—П —Д–Њ–ї–Є–∞—Ж–Є—П—В–∞ —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞ –љ–∞ —Б–Ї–Њ—А–Њ—Б—В 0,3 c. –Э–Њ —Б–µ–≥–∞ –Љ–Њ–ґ–µ–Љ –і–∞ —А–∞–Ј–≥–ї–µ–і–∞–Љ–µ –≤–µ–ї–Є—З–Є–љ–∞—В–∞ –љ–∞ –Ј–∞–±–∞–≤—П–љ–µ—В–Њ –љ–∞ –≤—А–µ–Љ–µ—В–Њ –Є –µ —В–Њ—З–љ–Њ —В–Њ–ї–Ї–Њ–≤–∞, ![]() . –Ї–Њ–ї–Ї–Њ—В–Њ —В—А—П–±–≤–∞ –і–∞ –±—К–і–µ —Б–њ–Њ—А–µ–і —В–µ–Њ—А–Є—П—В–∞ –љ–∞¬†–Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞.
. –Ї–Њ–ї–Ї–Њ—В–Њ —В—А—П–±–≤–∞ –і–∞ –±—К–і–µ —Б–њ–Њ—А–µ–і —В–µ–Њ—А–Є—П—В–∞ –љ–∞¬†–Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞.
–Ь–µ–ґ–і—Г –і—А—Г–≥–Њ—В–Њ, –∞–Ї–Њ —Б–Є –њ—А–µ–і—Б—В–∞–≤–Є–Љ, —З–µ —Б–µ –Њ–њ–Є—В–≤–∞–Љ–µ –і–∞ –љ–∞–Ї–∞—А–∞–Љ–µ –љ–∞—И–Є—П –љ–∞–±–ї—О–і–∞—В–µ–ї –і–∞ —Б–µ –і–≤–Є–ґ–Є вАЮ–њ–Њ-–±—К—А–Ј–Њ –Њ—В —Б–≤–µ—В–ї–Є–љ–∞—В–∞вАЬ,¬†—Й–µ –≤–Є–і–Є–Љ, —З–µ —В–Њ–≤–∞ –љ–µ¬†—Б—В–∞–≤–∞. –Ґ—К–є –Ї–∞—В–Њ –≤ —В–∞–Ј–Є –Ї–∞—А—В–Є–љ–∞ –љ—П–Љ–∞ –љ–∞—З–Є–љ –і–∞ —Б–µ –љ–∞–Ї–ї–Њ–љ—П—В¬†—Б–ї–Њ–µ–≤–µ—В–µ¬†–љ–∞ –њ–Њ–≤–µ—З–µ –Њ—В 45 ¬∞ –Є –≤—Б–µ –Њ—Й–µ –і–∞ —Б–µ –њ–Њ–і–і—К—А–ґ–∞—В –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—А—К–Ј–Ї–Є, –њ—А–Њ–Є–Ј—В–Є—З–∞—Й–Є –Њ—В –Ї–∞–Ј—Г–∞–ї–љ–Є—П –≥—А–∞—Д.
–Х–љ–µ—А–≥–Є—П, –Љ–∞—Б–∞, –≥—А–∞–≤–Є—В–∞—Ж–Є—П, —В—К–Љ–љ–∞ –Љ–∞—В–µ—А–Є—П –Є¬†–≤—Б–Є—З–Ї–Њ –Њ—Б—В–∞–љ–∞–ї–Њ
–Т–Њ–ї—Д—А–∞–Љ –Є–і–µ–љ—В–Є—Д–Є—Ж–Є—А–∞ –і–≤–∞ –≤–Є–і–∞ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є—П –≤ —Б–≤–Њ—П –Љ–Њ–і–µ–ї: –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–Њ–њ–Њ–і–Њ–±–љ–Є (—Е–Њ—А–Є–Ј–Њ–љ—В–∞–ї–љ–Є) –Є –≤—А–µ–Љ–µ–њ–Њ–і–Њ–±–љ–Є (–≤–µ—А—В–Є–Ї–∞–ї–љ–Є).

"–Т—Б—К—Й–љ–Њ—Б—В –≤ –љ–∞—И–Є—П –Љ–Њ–і–µ–ї –Є–Љ–∞ –љ–µ—Й–Њ, –љ–∞ –Ї–Њ–µ—В–Њ –Љ–Њ–ґ–µ–Љ –і–∞ –њ–Њ—Б–Њ—З–Є–Љ –Є –і–∞ –Ї–∞–ґ–µ–Љ вАЮ—В–Њ–≤–∞ –µ –µ–љ–µ—А–≥–Є—П!вАЬ, –Э–µ–Ј–∞–≤–Є—Б–Є–Љ–Њ –Њ—В —В–Њ–≤–∞, –Ї–∞–Ї–≤–∞ –µ –µ–љ–µ—А–≥–Є—П—В–∞. –Ґ–µ—Е–љ–Є—З–µ—Б–Ї–Њ—В–Њ —В–≤—К—А–і–µ–љ–Є–µ –µ: –µ–љ–µ—А–≥–Є—П—В–∞ —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞ –љ–∞ –њ–Њ—В–Њ–Ї–∞ –Њ—В –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—К–Ј–ї–Є –њ—А–µ–Ј –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–µ–љ–Њ–њ–Њ–і–Њ–±–љ–Є—В–µ —Е–Є–њ–µ—А–њ–Њ–≤—К—А—Е–љ–Њ—Б—В–Є. –Ш –Љ–µ–ґ–і—Г –і—А—Г–≥–Њ—В–Њ –Є–Љ–њ—Г–ї—Б—К—В —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞ –љ–∞ –њ–Њ—В–Њ–Ї–∞ –Њ—В –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –≤—К–Ј–ї–Є –њ—А–µ–Ј –≤—А–µ–Љ–µ–њ–Њ–і–Њ–±–љ–Є—В–µ —Е–Є–њ–µ—А–њ–Њ–≤—К—А—Е–љ–Њ—Б—В–Є", –Њ–±—П—Б–љ—П–≤–∞ –Т–Њ–ї—Д—А–∞–Љ.
–Я—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ–њ–Њ–і–Њ–±–љ–∞—В–∞ —Е–Є–њ–µ—А–њ–Њ–≤—К—А—Е–љ–Њ—Б—В –≤—Б—К—Й–љ–Њ—Б—В –µ —Б—В–∞–љ–і–∞—А—В–љ–∞ –Ї–Њ–љ—Ж–µ–њ—Ж–Є—П –≤ –Ю–±—Й–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞, –Ї–Њ—П—В–Њ –Є–Љ–∞ –њ—А—П–Ї–∞ –∞–љ–∞–ї–Њ–≥–Є—П –≤ –Љ–Њ–і–µ–ї–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ –Є –њ–Њ —Б—К—Й–µ—Б—В–≤–Њ —Б–µ –Њ–±—А–∞–Ј—Г–≤–∞ –Њ—В —Б–ї–Њ—П –≤—К–≤ —Д–Њ–ї–Є–∞—Ж–Є—П—В–∞.
–У—А–∞–≤–Є—В–∞—Ж–Є—П—В–∞ - –Њ–њ–Є—Б–∞–љ–∞ –Њ—В –Ю–±—Й–∞—В–∞ —В–µ–Њ—А–Є—П –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ—Б—В—В–∞ –љ–∞ –Р–є–љ—Й–∞–є–љ, –≤—К–Ј–љ–Є–Ї–≤–∞ –≤—К–≤ –≤—А—К–Ј–Ї–∞—В–∞ –Љ–µ–ґ–і—Г —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є—В–µ –≤ —Е–Є–њ–µ—А–≥—А–∞—Д–∞, –Ї–Њ–Є—В–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –Є–љ—В–µ—А–њ—А–µ—В–Є—А–∞–љ–Є –Ї–∞—В–Њ —З–∞—Б—В–Є—Ж–Є –Њ—В –Љ–∞—В–µ—А–Є—П—В–∞. –І–∞—Б—В–Є—Ж–Є—В–µ —Й–µ –±—К–і–∞—В –Љ–∞–ї–Ї–Є –≥—А—Г–њ–Є –Њ—В —Б–≤—К—А–Ј–∞–љ–Є —В–Њ—З–Ї–Є, –Ї–Њ–Є—В–Њ –њ—А–Њ–і—К–ї–ґ–∞–≤–∞—В –і–∞ —Б–µ –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞—В —Б –∞–Ї—В—Г–∞–ї–Є–Ј–∞—Ж–Є—П—В–∞ –љ–∞ —Е–Є–њ–µ—А–≥—А–∞—Д–∞.
–Т –Њ—Й–µ –њ–Њ-—Б–ї–Њ–ґ–љ–Њ —А–∞–Ј—И–Є—А–µ–љ–Є–µ –љ–∞ —В–µ–Ј–Є –Є–і–µ–Є –Т–Њ–ї—Д—А–∞–Љ –Є–Ј—Б–ї–µ–і–≤–∞ –Ї–∞–Ї —Б–≤–Њ–є—Б—В–≤–∞—В–∞ –љ–∞¬† —Е–Є–њ–µ—А–≥—А–∞—Д–Є—В–µ –і–Њ—А–Є —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞—В –љ–∞ —Б—В—А–∞–љ–љ–Є—В–µ —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є –љ–∞ –Ї–≤–∞–љ—В–Њ–≤–∞—В–∞ –Љ–µ—Е–∞–љ–Є–Ї–∞. вАЮ–Т –љ–∞—И–Є—В–µ –Љ–Њ–і–µ–ї–Є –Ї–≤–∞–љ—В–Њ–≤–∞—В–∞ –Љ–µ—Е–∞–љ–Є–Ї–∞ –µ –љ–µ –њ—А–Њ—Б—В–Њ –≤—К–Ј–Љ–Њ–ґ–љ–∞, —В—П –µ –∞–±—Б–Њ–ї—О—В–љ–Њ –љ–µ–Є–Ј–±–µ–ґ–љ–∞вАЭ, —В–≤—К—А–і–Є –Т–Њ–ї—Д—А–∞–Љ.
–Я—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ, –Є–Ј–≥—А–∞–і–µ–љ–Њ –≤ —В–∞–Ї–Є–≤–∞ —Е–Є–њ–µ—А–≥—А–∞—Д–Є, –Љ–Њ–ґ–µ –і–∞ –Є–Љ–∞ –Љ–љ–Њ–≥–Њ —Д–Є–љ–∞ —Б—В—А—Г–Ї—В—Г—А–∞, –Ї–∞—В–Њ —Б–µ–љ–Ј–Њ—А –Ј–∞ —Ж–Є—Д—А–Њ–≤–∞ –Ї–∞–Љ–µ—А–∞ —Б –љ–µ–≤–µ—А–Њ—П—В–љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –Љ–µ–≥–∞–њ–Є–Ї—Б–µ–ї–Є. –Т–Њ–ї—Д—А–∞–Љ –Є–Ј—З–Є—Б–ї—П–≤–∞, —З–µ —Е–Є–њ–µ—А–≥—А–∞—Д, –Њ—В–≥–Њ–≤–∞—А—П—Й –љ–∞ –і–љ–µ—И–љ–∞—В–∞ –Т—Б–µ–ї–µ–љ–∞, –Љ–Њ–ґ–µ –і–∞ –Є–Љ–∞ 10 500 —Б—В—К–њ–Ї–Є –≤—К–≤ –≤—А–µ–Љ–µ—В–Њ (–љ–µ—А–∞–Ј–±–Є—А–∞–µ–Љ–Њ –њ–Њ–≤–µ—З–µ –Њ—В –≤—К–Ј—А–∞—Б—В—В–∞ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞ –Ј–∞ —Б–µ–Ї—Г–љ–і–Є, –њ—А–Є–±–ї–Є–Ј–Є—В–µ–ї–љ–Њ 1015). –Ґ–∞–Ї–∞ —З–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –і–Њ—Б—В–∞—В—К—З–љ–Њ –Ј—К—А–љ–µ—Б—В–Њ, –Ј–∞ –і–∞ —Б—К–і—К—А–ґ–∞ —Б—В—А—Г–Ї—В—Г—А–Є –Њ—В —З–∞—Б—В–Є—Ж–Є –Љ–∞—В–µ—А–Є—П –Љ–љ–Њ–≥–Њ, –Љ–љ–Њ–≥–Њ –њ–Њ-–Љ–∞–ї–Ї–Є –Њ—В –Є–Ј–≤–µ—Б—В–љ–Є—В–µ —З–∞—Б—В–Є—Ж–Є –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞. –Т—Б—К—Й–љ–Њ—Б—В, –Т–Њ–ї—Д—А–∞–Љ –њ—А–µ–і–њ–Њ–ї–∞–≥–∞, —Б–≤—А—К—Е –Љ–∞–ї–Ї–Є –љ–µ–Є–Ј–≤–µ—Б—В–љ–Є —З–∞—Б—В–Є—Ж–Є, –Ї–Њ–Є—В–Њ —В–Њ–є –љ–∞—А–Є—З–∞ –Њ–ї–Є–≥–Њ–љ–Є, –Љ–Њ–ґ–µ –і–∞ —Б–∞ –±–Є–ї–Є —Б—К–Ј–і–∞–і–µ–љ–Є –≤ –Є–Ј–Њ–±–Є–ї–Є–µ –Љ–∞–ї–Ї–Њ —Б–ї–µ–і –љ–∞—З–∞–ї–Њ—В–Њ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞. –Ґ–∞–Ї–Є–≤–∞ –Њ–ї–Є–≥–Њ–љ–Є, –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–∞—Й–Є —Б–∞–Љ–Њ —Б –≥—А–∞–≤–Є—В–∞—Ж–Є—П—В–∞, –±–Є—Е–∞ –Љ–Њ–≥–ї–Є –і–∞ —Б–µ –љ–Њ—Б—П—В –≤—К–≤ –Є –Њ–Ї–Њ–ї–Њ –≥–∞–ї–∞–Ї—В–Є–Ї–Є—В–µ –љ–∞–њ—К–ї–љ–Њ –љ–µ–Ј–∞–±–µ–ї—П–Ј–∞–љ–Њ - —Б –Є–Ј–Ї–ї—О—З–µ–љ–Є–µ –љ–∞ –≥—А–∞–≤–Є—В–∞—Ж–Є–Њ–љ–љ–Њ—В–Њ –Є–Љ –≤—К–Ј–і–µ–є—Б—В–≤–Є–µ.
–°–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ –Њ–ї–Є–≥–Њ–љ–Є—В–µ –Љ–Њ–≥–∞—В –і–∞ –Њ–±—П—Б–љ—П—В –Ј–∞—Й–Њ –∞—Б—В—А–Њ–љ–Њ–Љ–Є—В–µ –Ј–∞–Ї–ї—О—З–∞–≤–∞—В –Ј–∞ —Б—К—Й–µ—Б—В–≤—Г–≤–∞–љ–µ—В–Њ –љ–∞ –Њ–≥—А–Њ–Љ–љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –љ–µ–≤–Є–і–Є–Љ–∞ "—В—К–Љ–љ–∞ –Љ–∞—В–µ—А–Є—П" –≤ –Ї–Њ—Б–Љ–Њ—Б–∞. (–Ш —В–Њ–≤–∞ —Б—К—Й–Њ –±–Є –Љ–Њ–≥–ї–Њ –і–∞ –Њ–±—П—Б–љ–Є –Ј–∞—Й–Њ –і–Њ—Б–µ–≥–∞ –Њ–њ–Є—В–Є—В–µ –Ј–∞ –Є–і–µ–љ—В–Є—Д–Є—Ж–Є—А–∞–љ–µ –љ–∞ –њ—А–Є—А–Њ–і–∞—В–∞ –љ–∞ —В—К–Љ–љ–∞—В–∞ –Љ–∞—В–µ—А–Є—П –±—П—Е–∞ –љ–µ—Г—Б–њ–µ—И–љ–Є.)
–Я–Њ —Б—К—Й–Є—П –љ–∞—З–Є–љ –Љ–Є—Б—В–µ—А–Є–Њ–Ј–љ–∞—В–∞ вАЮ—В—К–Љ–љ–∞ –µ–љ–µ—А–≥–Є—ПвАЬ, –Ї–Њ—П—В–Њ –Ї–∞—А–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞ –і–∞ —Б–µ —А–∞–Ј—И–Є—А—П–≤–∞ —Б —Г—Б–Ї–Њ—А—П–≤–∞—Й–∞ —Б–µ —Б–Ї–Њ—А–Њ—Б—В, –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –њ—А–Њ—Б—В–Њ –µ—Б—В–µ—Б—В–≤–µ–љ–∞ –Њ—Б–Њ–±–µ–љ–Њ—Б—В –љ–∞ —Е–Є–њ–µ—А–≥—А–∞—Д–Є—В–µ –љ–∞ –Т–Њ–ї—Д—А–∞–Љ. –Ь–Њ–ґ–µ –±–Є —В—К–Љ–љ–∞—В–∞ –µ–љ–µ—А–≥–Є—П –њ–Њ —Б—К—Й–µ—Б—В–≤–Њ –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ –њ—А–Њ—Б—В–Њ —В–Њ–≤–∞, –Њ—В –Ї–Њ–µ—В–Њ –µ –љ–∞–њ—А–∞–≤–µ–љ–Њ —Б–∞–Љ–Њ—В–Њ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ.
–Ю—В–≤—К–і —В–Њ–≤–∞ –Т–Њ–ї—Д—А–∞–Љ —Б–Љ—П—В–∞, —З–µ –љ–µ–≥–Њ–≤–Є—В–µ —Е–Є–њ–µ—А–≥—А–∞—Д–Є –Љ–Њ–≥–∞—В –і–∞ —А–∞–Ј—А–µ—И–∞—В —В–µ–Ї—Г—Й–Є—В–µ —Б–њ–Њ—А–Њ–≤–µ –Ј–∞ —В–Њ–≤–∞ –Ї–Њ—П –Њ—В –Љ–љ–Њ–≥–Њ —Б–њ–µ–Ї—Г–ї–∞—В–Є–≤–љ–Є —В–µ–Њ—А–Є–Є —Б–∞ –љ–∞–є-–і–Њ–±—А–Є—В–µ –Ј–∞–ї–Њ–Ј–Є –Ј–∞ –Њ–±—П—Б–љ–µ–љ–Є–µ –љ–∞ —Д—Г–љ–і–∞–Љ–µ–љ—В–∞–ї–љ–∞—В–∞ —Д–Є–Ј–Є–Ї–∞. –Ґ–Њ–≤–∞ —Б–∞ —В–µ–Њ—А–Є—П—В–∞ –љ–∞ —Б—Г–њ–µ—А—Б—В—А—Г–љ–Є—В–µ, –Ї–≤–∞–љ—В–Њ–≤–∞—В–∞ –≥—А–∞–≤–Є—В–∞—Ж–Є—П, –њ—А–Є—З–Є–љ–љ–Њ-—Б–ї–µ–і—Б—В–≤–µ–љ–Є—В–µ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –Є –і—А—Г–≥–Є –Є–і–µ–Є —Б–∞ –њ—А–µ–і–ї–∞–≥–∞–љ–Є –Є –Њ–±—Б—К–ґ–і–∞–љ–Є –Њ—В –і–µ—Б–µ—В–Є–ї–µ—В–Є—П. –Т–Њ–ї—Д—А–∞–Љ —Б–Љ—П—В–∞, —З–µ —Е–Є–њ–µ—А–≥—А–∞—Д–Є—В–µ –Љ–Њ–≥–∞—В –і–∞ —Б—К–і—К—А–ґ–∞—В –≤—Б–Є—З–Ї–Є —В—П—Е.
вАЮ–Я–Њ—З—В–Є –Є–Ј–≥–ї–µ–ґ–і–∞, —З–µ –≤—Б–Є—З–Ї–Є —Б–∞ –±–Є–ї–Є –њ—А–∞–≤–Є –њ—А–µ–Ј —Ж—П–ї–Њ—В–Њ –≤—А–µ–Љ–µвАЬ, –њ–Є—И–µ —В–Њ–є, вАЮ–Є –њ—А–Њ—Б—В–Њ –µ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Њ –і–∞ —Б–µ –і–Њ–±–∞–≤–Є –љ–Њ–≤–∞ —Б—Г–±—Б—В–∞–љ—Ж–Є—П, –Ј–∞ –і–∞ –≤–Є–і–Є—В–µ –Ї–∞–Ї –≤—Б–Є—З–Ї–Њ —Б–µ –≤–њ–Є—Б–≤–∞ –Ј–∞–µ–і–љ–Њ.вАЬ
–Т–Њ–ї—Д—А–∞–Љ –Ї–∞–љ–Є –Њ–±—Й–љ–Њ—Б—В—В–∞ –љ–∞ —Д–Є–Ј–Є—Ж–Є—В–µ –і–∞ —Г—З–∞—Б—В–≤–∞ –≤ –Њ–±—Б—К–ґ–і–∞–љ–µ—В–Њ –љ–∞ –љ–µ–≥–Њ–≤–∞—В–∞ –≤–Є–Ј–Є—П.
вАЮ–Т –Ї—А–∞–є–љ–∞ —Б–Љ–µ—В–Ї–∞ –љ–∞—И–∞—В–∞ —Ж–µ–ї —В—А—П–±–≤–∞ –і–∞ –±—К–і–µ –і–∞ –Є–Ј–≥—А–∞–і–Є–Љ –Љ–Њ—Б—В, –Ї–Њ–є—В–Њ –і–∞ —Б–≤—К—А–Ј–≤–∞ –љ–∞—И–Є—В–µ –Љ–Њ–і–µ–ї–Є —Б—К—Б —Б—К—Й–µ—Б—В–≤—Г–≤–∞—Й–Є—В–µ –Ј–љ–∞–љ–Є—П –Ј–∞ —Д–Є–Ј–Є–Ї–∞—В–∞вАЬ, –њ–Є—И–µ —В–Њ–є. вАЮ–Р–Ј —Б—К–Љ –Є–Ј–Ї–ї—О—З–Є—В–µ–ї–љ–Њ –Њ–њ—В–Є–Љ–Є—Б—В, —З–µ –љ–∞–є-–љ–∞–Ї—А–∞—П —Б–Љ–µ –љ–∞ –њ—А–∞–≤–Є–ї–љ–Є—П –њ—К—ВвАЬ –Ї—К–Љ –љ–∞–Љ–Є—А–∞–љ–µ—В–Њ –љ–∞ вАЮ–њ—А–∞–≤–Є–ї–љ–Њ—В–ЊвАЬ –њ—А–∞–≤–Є–ї–Њ –Ј–∞ –љ–∞—И–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞.
–Ґ–Њ–≤–∞ вАЮ–њ—А–∞–≤–Є–ї–љ–Њ –њ—А–∞–≤–Є–ї–ЊвАЬ –±–Є –≥–µ–љ–µ—А–Є—А–∞–ї–Њ —Е–Є–њ–µ—А–≥—А–∞—Д —Б —В–Њ—З–љ–Є—В–µ —Б–≤–Њ–є—Б—В–≤–∞ –љ–∞ –љ–∞—И–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞: —В—А–Є (–њ—А–Є–≤–Є–і–љ–Њ) –Є–Ј–Љ–µ—А–µ–љ–Є—П –љ–∞ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ, –њ—А–∞–≤–Є–ї–љ–∞—В–∞ —Б–Ї–Њ—А–Њ—Б—В –љ–∞ —А–∞–Ј—И–Є—А–µ–љ–Є–µ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞, –њ—А–∞–≤–Є–ї–љ–Є—П –љ–∞–±–Њ—А¬† –µ–ї–µ–Љ–µ–љ—В–∞—А–љ–Є —З–∞—Б—В–Є—Ж–Є —Б –њ—А–∞–≤–Є–ї–љ–Є—В–µ –Ј–∞—А—П–і–Є –Є –Љ–∞—Б–Є –Є –і—А—Г–≥–Є —Е–∞—А–∞–Ї—В–µ—А–Є—Б—В–Є–Ї–Є.
–Э–Њ –Љ–Њ–ґ–µ –±–Є –Т–Њ–ї—Д—А–∞–Љ –µ –Њ—Б—К–Ј–љ–∞–ї, —З–µ —В—К—А—Б–µ–љ–µ—В–Њ –љ–∞ –µ–і–љ–Њ –µ–і–Є–љ—Б—В–≤–µ–љ–Њ –њ—А–∞–≤–Є–ї–Њ –њ—А–Њ–њ—Г—Б–Ї–∞ –љ–µ—Й–Њ –њ–Њ-–≥–Њ–ї—П–Љ–Њ. –Ь–Њ–ґ–µ –±–Є –Т—Б–µ–ї–µ–љ–∞—В–∞ –Є–Ј–њ–Њ–ї–Ј–≤–∞ –≤—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—А–∞–≤–Є–ї–∞. –Ґ–Њ–≥–∞–≤–∞ –≤—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –≤—Б–µ–ї–µ–љ–Є —Б–∞ —Б–∞–Љ–Њ —З–∞—Б—В–Є –Њ—В –µ–і–љ–∞ –љ–∞–Є—Б—В–Є–љ–∞ –≥–Њ–ї—П–Љ–∞ –≤—Б–µ–ї–µ–љ–∞, –≤ –Ї–Њ—П—В–Њ вАЮ–∞–±—Б–Њ–ї—О—В–љ–Њ –≤—Б–Є—З–Ї–ЊвА¶ –Љ–Њ–ґ–µ –і–∞ —Б–µ —Б–ї—Г—З–Є - –≤–Ї–ї—О—З–Є—В–µ–ї–љ–Њ –≤—Б–Є—З–Ї–Є —Б—К–±–Є—В–Є—П –Ј–∞ –≤—Б–Є—З–Ї–Є –≤—К–Ј–Љ–Њ–ґ–љ–Є –њ—А–∞–≤–Є–ї–∞.вАЬ
–†–∞–Ј–ї–Є—З–∞–≤–∞–Љ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ –љ–∞–±–Њ—А –Њ—В —Д–Є–Ј–Є—З–µ—Б–Ї–Є –Ј–∞–Ї–Њ–љ–Є, –±–∞–Ј–Є—А–∞–љ–Є –љ–∞ вАЮ–µ–Ј–Є–Ї–∞вАЬ, –Ї–Њ–є—В–Њ –Є–Ј–њ–Њ–ї–Ј–≤–∞–Љ–µ –Ј–∞ –Њ–њ–Є—Б–∞–љ–Є–µ –Є —А–∞–Ј–±–Є—А–∞–љ–µ –љ–∞ —Б–≤–µ—В–∞. –Х–ї–µ–Љ–µ–љ—В–Є—В–µ –љ–∞ —В–Њ–Ј–Є –µ–Ј–Є–Ї —Б–∞ –љ–∞—Б—В—А–Њ–µ–љ–Є –љ–∞ вАЮ–≤–Є–і–Њ–≤–µ—В–µ –љ–µ—Й–∞, –Ї–Њ–Є—В–Њ —Б–µ—В–Є–≤–∞—В–∞ –љ–Є –Њ—В–Ї—А–Є–≤–∞—В, –Є–Ј–Љ–µ—А–≤–∞—В–µ–ї–љ–Є—В–µ –љ–Є —Г—А–µ–і–Є –Є –љ–∞—И–∞—В–∞ —Б—К—Й–µ—Б—В–≤—Г–≤–∞—Й–∞ —Д–Є–Ј–Є–Ї–∞ –Њ–њ–Є—Б–≤–∞вАЬ. –Я—А–∞–≤–Є–ї–љ–Њ—В–Њ –њ—А–∞–≤–Є–ї–Њ –µ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ —Б—К–Њ—В–≤–µ—В—Б—В–≤–∞ –љ–∞ —З–∞—Б—В—В–∞ –Њ—В —Е–Є–њ–µ—А–≥—А–∞—Д–∞, –Ї–Њ—П—В–Њ –Є–Ј—Б–ї–µ–і–≤–∞–Љ–µ –Њ—В –љ–∞—И–∞—В–∞ —Б–Њ–±—Б—В–≤–µ–љ–∞ –Ї–Њ–љ–Ї—А–µ—В–љ–∞ —А–µ—Д–µ—А–µ–љ—В–љ–∞ —А–∞–Љ–Ї–∞. –Ц–Є–≤–Њ—В—К—В –і—А—Г–≥–∞–і–µ –Љ–Њ–ґ–µ –і–∞ –≤–Є–і–Є –љ–µ—Й–∞—В–∞ –њ–Њ —А–∞–Ј–ї–Є—З–µ–љ –љ–∞—З–Є–љ. вАЮ–Т—Б—К—Й–љ–Њ—Б—В –Є–Љ–∞ –њ–Њ—З—В–Є –±–µ–Ј–Ї—А–∞–є–љ–Њ –Љ–љ–Њ–≥–Њ–Њ–±—А–∞–Ј–Є–µ –Њ—В —А–∞–Ј–ї–Є—З–љ–Є –љ–∞—З–Є–љ–Є –і–∞ –Њ–њ–Є—И–µ–Љ –Є –њ—А–µ–ґ–Є–≤–µ–µ–Љ –љ–∞—И–∞—В–∞ –≤—Б–µ–ї–µ–љ–∞вАЬ, –њ—А–µ–і–њ–Њ–ї–∞–≥–∞ –Т–Њ–ї—Д—А–∞–Љ.
–° –і—А—Г–≥–Є –і—Г–Љ–Є, –Њ–±—П—Б–љ—П–≤–∞–љ–µ—В–Њ –љ–∞ —Д–Є–Ј–Є–Ї–∞—В–∞, –Ї–Њ—П—В–Њ —Б–µ –њ—А–Є–ї–∞–≥–∞ –Ј–∞ –љ–∞—И–µ—В–Њ —Б—К—Й–µ—Б—В–≤—Г–≤–∞–љ–µ, –Љ–Њ–ґ–µ –і–∞ –Є–Ј–Є—Б–Ї–≤–∞ –≤–љ–Є–Ї–≤–∞–љ–µ –≤ –Љ–µ—Е–∞–љ–Є–Ј–Љ–Є—В–µ –љ–∞ –µ–і–љ–∞ –Љ–љ–Њ–≥–Њ –њ–Њ-—Б–ї–Њ–ґ–љ–∞ —А–µ–∞–ї–љ–Њ—Б—В, –Є–Ј–≤—К–љ —Б—Д–µ—А–∞—В–∞ –љ–∞ —В–Њ–≤–∞, –Ї–Њ–µ—В–Њ –Љ–Њ–ґ–µ–Љ –і–∞ –њ—А–µ–ґ–Є–≤–µ–µ–Љ. –Ъ–∞–Ї—В–Њ –Т–Њ–ї—Д—А–∞–Љ –Ї–∞–Ј–≤–∞: вАЮ–Т –Љ–љ–Њ–≥–Њ –Њ—В–љ–Њ—И–µ–љ–Є—П –љ–µ–Љ–Є–љ—Г–µ–Љ–Њ —Б–µ –њ—К—А–Ј–∞–ї—П–Љ–µ –љ–∞ —А—К–±–∞ –љ–∞ –Њ–љ–Њ–≤–∞, –Ї–Њ–µ—В–Њ —Е–Њ—А–∞—В–∞ –Љ–Њ–≥–∞—В –і–∞ —А–∞–Ј–±–µ—А–∞—В.вАЬ
–Ш –≤—Б–µ –њ–∞–Ї –Њ—Б–љ–Њ–≤–љ–Є—В–µ —Д–Є–Ј–Є—Ж–Є –Њ—В–і–∞–≤–љ–∞ –њ–Њ–і–Њ–Ј–Є—А–∞—В, —З–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є –≤—А–µ–Љ–µ—В–Њ –љ–µ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –Њ—Б–љ–Њ–≤–љ–Є –њ–Њ–љ—П—В–Є—П. –Я–Њ-—Б–Ї–Њ—А–Њ –Є–Ј–≥–ї–µ–ґ–і–∞, —З–µ –њ—А–Њ—Б—В—А–∞–љ—Б—В–≤–Њ—В–Њ –Є –≤—А–µ–Љ–µ—В–Њ —Б–∞ —Г—Б–ї–Њ–≤–љ–Њ—Б—В–Є, –Ї–Њ–Є—В–Њ —В—А—П–±–≤–∞ –і–∞ —Б–∞ –≤—К–Ј–љ–Є–Ї–љ–∞–ї–Є –Њ—В –љ–µ—Й–Њ –њ–Њ-–і—К–ї–±–Њ–Ї–Њ. –Ґ–Њ–≤–∞ –Љ–Њ–ґ–µ –і–∞ –µ —Б–Љ–µ–ї–Њ –њ—А–µ–і–њ–Њ–ї–Њ–ґ–µ–љ–Є–µ, –љ–Њ –њ—А–Њ—Б—В–Њ –Љ–Њ–ґ–µ –±–Є –Т–Њ–ї—Д—А–∞–Љ –µ –≤—К–Ј–њ—А–Є–µ–ї –њ—К—В, –Ї–Њ–є—В–Њ –≤–Њ–і–Є –і–Њ –і—К–ї–±–Є–љ–Є—В–µ, –Њ—В–Ї—К–і–µ—В–Њ –≤—К–Ј–љ–Є–Ї–≤–∞ —А–µ–∞–ї–љ–Њ—Б—В—В–∞.
–°–∞–Љ–Њ –≤—А–µ–Љ–µ—В–Њ - –Є–ї–Є –Њ—Й–µ –Љ–љ–Њ–≥–Њ —Б—В—К–њ–Ї–Є –Ј–∞ –∞–Ї—В—Г–∞–ї–Є–Ј–Є—А–∞–љ–µ –љ–∞ —Е–Є–њ–µ—А–≥—А–∞—Д–∞ - —Й–µ –њ–Њ–Ї–∞–ґ–µ.
–°–њ—А–∞–≤–Ї–∞:
A Class of Models with the Potential to Represent Fundamental Physics, technical introduction, Stephen Wolfram
Some Relativistic and Gravitational Properties of the Wolfram Model (pdf), Jonathan Gorard
Some Quantum Mechanical Properties of the Wolfram Model (pdf), Jonathan Gorard
–Ш–Ј—В–Њ—З–љ–Є–Ї:
Finally We May Have a Path to the Fundamental Theory of PhysicsвА¶ and ItвАЩs Beautiful, –њ–Њ–њ—Г–ї—П—А–љ–Њ –Њ–±—П—Б–љ–µ–љ–Є–µ –љ–∞ –°—В–Є–≤—К–љ –Т–Њ–ї—Д—А–∞–Љ
Stephen WolframвАЩs hypergraph project aims for a fundamental theory of physics,¬†sciencenews
–Ю—Й–µ –њ–Њ —В–µ–Љ–∞—В–∞
–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Ь–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞ –њ—А–Њ–≥—А–∞–Љ–∞ –Љ–Њ–ґ–µ –і–∞ –њ–Њ–Љ–Њ–≥–љ–µ –і–∞ —Б–µ —А–∞–Ј–±–µ—А–µ —Д–Њ—А–Љ–∞—В–∞ –љ–∞ –Т—Б–µ–ї–µ–љ–∞—В–∞

–§–Є–Ј–Є–Ї–∞
–Ю—В–Ї—А–Є—Е–∞ –≤ –Ї–≤–∞–љ—В–Њ–≤ –Љ–∞—В–µ—А–Є–∞–ї —Д—А–∞–Ї—В–∞–ї–љ–Є –Љ–Њ–і–µ–ї–Є –Є –њ–∞–Љ–µ—В

–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Ъ–∞–Ї –і–∞ –њ—А–µ–±—А–Њ–Є–Љ —З–Є—Б–ї–∞—В–∞, –±–µ–Ј –і–∞ –≥–Є –±—А–Њ–Є–Љ –Є–ї–Є –Ј–∞—Й–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞—В–∞ –µ –Ї—А–∞—Б–Є–≤–∞




















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
7011
2
10.05 2020 –≤ 09:22
–°—В—А–∞—Е–Њ—В–љ–∞ —Б—В–∞—В–Є—П - –љ—О –і–∞–ґ–µ –Љ–Є —Б–µ —Б—В–Њ—А–Є –Ї—А–∞—В–Ї–∞. –Т–Њ–ї—Д—А–∞–Љ –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П—В–∞ —Б–∞ –Љ–Є —Б–њ–∞—Б—П–≤–∞–ї–Є –Ї–Њ–ґ–∞—В–∞ –і–Њ—Б—В–∞ —З–µ—Б—В–Њ. –Т—Б–Є—З–Ї–Њ —В–∞–Љ –Є —В—Г–Ї –≤ —Б—В–∞—В–Є—П—В–∞ –µ –Њ–±—П—Б–љ–µ–љ–Њ –і–Њ—Б—В–∞ –∞–і–µ–Ї–≤–∞—В–љ–Њ –Њ—В –Ї–Њ–ї–Ї–Њ—В–Њ –≤ —Б—К–Њ—В–≤–µ–љ–Є—П—В –Ї—Г—А—Б –њ–Њ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–∞ –љ–∞ –Ь–Ю–Э.
–Ф–Њ –Ї–Њ–ї–µ–≥–∞—В–∞ - —Б—К–ґ–∞–ї—П–≤–∞–Љ –≥—А–∞—Д–∞ —Б–Є –µ –≥—А–∞—Д - –Ї–∞–Ї—В–Њ –Ї–∞–Ј–≤–∞—И–µ –∞—Б–Є—Б—В–µ–љ—В–∞ –њ–Њ –Т–Ь - —Б–Љ–µ–љ–Є–Љ –ї–Є –Є–Љ–µ—В–Њ, –≥—Г–±–Є —В–Є—В–ї–∞—В–∞!
14618
1
21.04 2020 –≤ 10:14
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
–•—А–Є—Б—В–Є—П–љ–Є–љ
–Ґ–Њ–≤–∞ –µ –Ї—А–∞–ї—П—В –љ–∞ —В–Є–Ї–≤–Є—В–µ: –Ґ–Є–Ї–≤–∞—В–∞ –Љ—Г —В–µ–ґ–Є –љ–∞–і –µ–і–Є–љ –µ–і–Є–љ —В–Њ–љ
dolivo
–°–∞—Е–∞—А–∞ –Њ—З–∞–Ї–≤–∞ 75% —Г–≤–µ–ї–Є—З–µ–љ–Є–µ –љ–∞ –≤–∞–ї–µ–ґ–Є—В–µ –і–Њ 2100 –≥.
dolivo
–Ч–µ–Љ–љ–∞—В–∞ —П–±—К–ї–Ї–∞: —Б—В–∞—А–∞ –Ї—Г–ї—В—Г—А–∞ –Ј–∞ –љ–Њ–≤–Є—В–µ –Ї–ї–Є–Љ–∞—В–Є—З–љ–Є –≤—А–µ–Љ–µ–љ–∞