Математическа програма, която визуализира вътрешността на странни 3D пространства, може да ни помогне да разберем формата на Вселената.
Хенри Сегерман (Henry Segerman) от Университета на Оклахома и неговите колеги работят по интерактивното картиране на вътрешността на математическите пространства, известни като триизмерни многообразия, използвайки програма, наречена SnapPy.
„Мисля за тези неща от 20 години, но никога не сме имали изображения“, разказва Сегерман.
Триизмерното многообразие е като обобщена версия на обикновено триизмерно пространство. „Триизмерното многообразие е нещо, което прилича на триизмерното пространство, ако погледнете само малък участък от него“, обяснява Сегерман.
Различните многообразия могат или не могат да имат граница. „Може да има място, където не можете да продължите по-нататък“, разказва Сегерман.
За да стане по-ясно, да си представим двуизмерно многообразие, което е обобщена версия на двуизмерното пространство. Двуизмерното многообразие може да бъде плоско пространство, което продължава безкрайно, но може също да бъде сфера или лента на Мьобиус, по която можете да се движите безкрайно и никога да не стигнете ръб.
Екипът разглежда триизмерни многообразия с форма на възел, отстранен от тях. „Триизмерните многообразия, от които сме премахнали възела имат граница там, където преди е бил възелът“, казва Сегерман.
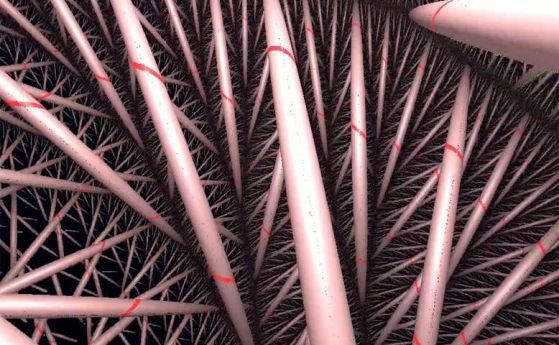
Това премахване има странни ефекти върху пространството. Например розовите топки се трансформират във форми на пръчки, тъй като програмата предлага различни геометрии вътре, където е възелът (вижте изображенията по-горе).
„Не можете да използвате обикновена графика, както в компютърните игри“, обяснява Сегерман. 'Трябва да се изгради от нулата".
Една от темите на този клон от математиката, наречен топология, е формата на Вселената. „Продължава ли безкрайно във всички посоки? По някакъв начин върти ли се около себе си? “, се пита Сегерман. „Не можем да видим достатъчно далеч, за да знаем.“
Екипът се надява, че други математици могат да използват програмата за визуализации, която може да доведе до бъдещи идеи.
Източник:
Trippy maths program could help figure out the shape of the universe, NewScientist
Що е то топология?
Топология като клон на математиката е плод на въображението на ХХ век. Топологичните идеи са проникнали почти всички области на математиката, както и в съвременната физика и технология. Без топологични знания е невъзможен математическия анализ, решаването на сложни системи на диференциални уравнения (например описание на физическите полета или атмосферни явления) и дори проектирането на печатни платки.
Топологията е наука за непрекъснатостта. В математиката една функция се казва, че е непрекъсната, ако една малка промяна на аргумента, причинява само малка промяна в резултата. Ако това не е така, за функцията се казва, че е прекъсната.
Според една популярна шега тополозите са такива шемети, които не различават чаша за кафе от геврек - и двете са тела с една дупка. И наистина в топологията формата е без значение - обектите са все едно направени от фантастично еластичен материал, който можем да огъваме, разтегляме и мачкаме колкото си искаме, но без да ги чупим, разрушаваме или им правим дупки.
Какво означава "без край" в топологията
Вътрешна точка на геометричен обект е такава точка, когато не само тя принадлежи на обекта, а и всичките й съседните точки също принадлежат на обекта. А при една крайна точка не всички съседни точки принадлежат на обекта. Под край разбираме тези точки от обекта, които не са вътрешни, т.е такава точка, при която не всички нейни съседни точки принадлежат на обекта. Краят на кръга е окръжността, а на кълбото - сферата. Правата няма край.
Що е то "многообразие"
Многообразието е математическо понятие, обобщаващо за кое да е измерение понятията за линии, повърхности (а и пространства), не съдържащи особени точки (без точки на самопресечане, крайни точки и др.). За пример за едномерно многообразие може да служи правата, окръжността, елипсата и въобще всяка линия, чиито точки, заедно с околноста си от съседни точки са взаимно еднозначни и непрекъснати или, както казват в топологията, хомеоморфни на интервал. Под интервал се разбира в топологията вътрешната част от отсечка, без крайните 2 точки. Ще кажете, ако махнем крайните 2, ще останат други 2 крайни, но случаят, ако се замислим не е такъв. Ако имаме отсечка с крайни точки 0 и 1, кои ще са крайните точки на интервала й? 0.5? 0.001? 0.00000001? За "съседството" в топологията не се определят разстояния, те може да са безкрайно малки. Аналогично пример за двумерно многообразие е кръг, на който сме махнали крайната окръжност, а за тримерно - кълбо, на което сме одрали външната сфера.
Ако един обект, независимо от каква размерност, плосък, триизмерен или n-мерен, може чрез деформация (без разкъсване и слепване) да се превърне в друг, ние ги наричаме хомеоморфни. Хомеоморфни са например кълбото и куба. Но не бихме могли да направим от кълбото геврек, ако спазваме правилата на топологията.
Крупномащабната геометрия на Вселената е фундаментален проблем на космологията, особено важни са пространствената й кривина и топология. Уравненията на Айнщайн за гравитационното поле определят само локалните свойства на пространство-времето, но и не глобалната структура на Вселената като цяло.
В исторически контекст великите теоретически открития в математиката по правило имат последствия, които ще наблюдаваме тепърва в бъдеще.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари