„Животът няма да бъде същият дълго време“, казва Джулия Гог (Julia Gog), математик от Университета в Кеймбридж.
Животът на Гог рязко се променя в началото на февруари, когато тя изоставя нормалните си задължения в Центъра за математически науки и започна да посвещава всичките си усилия на SPI-M, група за моделиране, която подава своите резултати в Научно-консултативната група за извънредни ситуации (SAGE). SPI-M работи известно време в готовност за грипна пандемия, но сега е насочена изцяло върху пандемията на COVID-19.
Задачата на SPI-M е да разработи и използва математически модели, които могат да ни помогнат да прогнозираме какво ще се случи по-нататък и как различните интервенции могат да променят това - как ще се развие пандемията COVID-19 и какъв ефект ще имат социалните мерки, в условията на които живеем всички сега.
Но какви са тези модели и дали са точни?
Моделите
Ако сте чували, че броят на инфекциите с COVID-19 се удвоява на всеки три дни, може би ще разберете, че ако днес имаме x случаи и тази тенденция продължава, тогава ще имаме
2x случая за 3 дни,
4x случая за 6 дни,
8x случая за 9 дни
и като цяло 2nx за 3*n дни. Това е стръмният растеж, довел до това бедствие.
Тази екстраполация, толкова проста, колкото е възможно, подчертава основните елементи на модела - математически израз, който описва общия характер на промяната, която ще се случи с времето, и параметри, които определят точната форма на промяната. В нашия пример имаме експоненциален растеж във времето и стръмността на този растеж се определя от параметъра на времето на удвояване, което е 3 дни.
Моделът SIR
Можете да разберете повече за модела SIR в тази статия.
Ако искаме по-дългосрочни прогнози и да симулираме в детайли въздействието на интервенциите (предприетите мерки за ограничение на движението, карантина, затварянето на училища, търговски центрове и т.н.), се нуждаем от по-сложен модел. Различните модели са проектирани за различни цели, като например да правят краткосрочни прогнози, дългосрочни прогнози или да симулират ефекта от конкретни мерки, като затварянето на училищата. Но макар моделите се различават, те обикновено се изграждат около подход, който съществува от 10-те години: моделът SIR.
За да разберете общата идея на модела SIR, представете си популация от хора, изложени на вируса, в която всички са податливи на заболяването (S - susceptible), заразени (I - infectious) или възстановени и следователно придобили имунитет (R - recovered). Начинът, по който хората преминават от S клас в I класа, а след това от I клас в клас R, се описва с математически уравнения. Тези уравнения зависят от скоростта на предаване на болестта, както и от скоростта на възстановяване. Започваме модела само с малка част от популацията в I клас и след това го оставяме да се развива с течение на времето, наблюдавайки как се разпространява болестта и след това отшумява, докато хората се възстановяват и придобиват имунитет.
Движение между класовете на модела SIR
Макар и прост, моделът SIR дава добри прогнози за прости популации, като например ученици в интернат. Когато става въпрос за по-сложни популации, може да се свържат много отделни модели SIR, представящи различни географски местоположения и подгрупи, включително например отделни градове или училища.
Контактите са ключови
В този контекст са изключително важни моделите на контакти между хората: кой с кого се среща и колко често. Информацията за това идва от проучванията за смесването в обществото.
Пример е мащабен научен проект, който се проведе през 2018 г. в сътрудничество между BBC и екипа на Гог. Участниците изтеглят приложение, което проследява движенията им, а те си записват хората, с които се срещат (анонимно). Тези данни за контактите се представят математически от масиви (матрици) от числа (виж фигурата по-долу), които се вграждат в модела.
Контактна матрица, показваща средния брой контакти между различни възрастови групи. По-тъмните нюанси означават повече контакти (тук цветовете се използват вместо числа, за да стане матрицата по-нагледна). Илюстрацията е от статията Contagion! BBC Pandemic Four – The model behind the documentary.
За да видите как определена социална мярка, като затваряне на училища, може да повлияе на разпространението на болестта, съответно се адаптират данните за контактите, като се премахват или мащабират части от тях, които са свързани с някаква интервенция.
Но трябва да се внимава.
„Изключването изцяло на влиянието на училищния компонент е нереалистично, то просто трябва да бъде намалено“, препоръчва Гог. "И ако няма ясни насоки, тогава децата извън училище може да се смесят в обществото по други начини, например с бабите и дядовците си, което означава, че ще се случват допълнителни контакти, които трябва да бъдат взети под внимание. Въпреки че можем само да гадаем в каква степен ще са".
Съществуващите данни, като например информация за случилото се по време на стачки на учители, могат да ни помогнат да калибрираме нашите данни за контактите, за да отразят мерките и да се прогнозира техния ефект върху епидемията.
Но дават ли верен резултат моделите?
Вместо един модел, предназначен да представи цяла държава, Европа или дори целия свят, има много различни модели, предназначени да правят различни неща и въпреки че подхода на подразделяне на модела SIR е основна парадигма, моделите все пак могат да бъдат различни по своето естество. Някои от тях са напълно детерминирани, други съдържат степен на случайност, някои са създадени да се изпълняват само веднъж, за да демонстрират ролята на един конкретен фактор, други се изпълняват много пъти, за да се получат диапазони от прогнози в условията на несигурност.
Големият въпрос е дали моделите са реалистични.
Един от проблемите е, че COVID-19 е ново заболяване, но съществуват модели за сезонния грип.
„Всички започнахме от грип, никой нямаше модел на пандемия на коронавирус“, разказва Гог. „Така че в началото на тази пандемия трябваше да се опитаме да разберем какво може да е систематично различно между COVID-19 и типичните модели, които бяхме изградили за грипа“.
Въпреки че динамиката на пандемията е сходна при грипа и коронавируса, има някои разлики. Първата е, че при COVID-19 има голям латентен период - човек може да е заразен, без да прояви никакви симптоми.
При грипа симптомите се проявяват след няколко часа от заразяването, но за коронавируса може да изминат няколко дена.
По отношение на модела това означава да преминем от SIR в SEIR, където E означава exposed („изложени“): хората от този клас имат инфекция, но все още нямат симптоми. Класът Е може да бъде разделен допълнително на такива, които са заразни за другите и такива, които не са.
„Всички модели са приблизителни и за грипа често може да се мине с SIR, в зависимост от това, за какво е предназначен моделът. Но пренебрегването на латентния период за този вирус би било много лошо приближение".
Това е типичният изход от обикновен модел SIR. Броят на хората, податливи на болестта, е показан в син цвят, броят на заразените е в зелено и броят на възстановените е в червено.
Има и много други неща, които не знаем за COVID-19.
"Има някои подробности, които просто не знаем, например точно колко сме заразни в първия ден или на втория ден", коментира Гог. „Да се предположи на база несъвършените ни данни е много трудно, макар че сега имаме някои данни от Китай и други страни, а данните от круизните кораби бяха много интересни. Просто се опитваме да направим всичко възможно да екстраполираме от ограничена информация“.
Когато няма достатъчно информация хората, които правят моделите, решават кои от неизвестните са най-важни за развитието на модела, за да се премахне несигурността - извършването на такива промени е критично важен аспект на моделирането.
Значението на всеки един параметър може да зависи от това какво точно се опитваме да направим.
"За да прогнозираме колко случаи ще има утре, не е нужно да знаем много неща. В момента това е почти експоненциално", разказва Гог. "Но за да направим прогноза дали ще има втора вълна, трябва да знаем много различни неща."
Важен фактор за по-дългосрочните прогнози е базовото число на репродукция на заболяването (често обозначавано като R0): броят на хората, които заразен човек ще зарази средно, като се предполага, че всички в популацията са податливи на заболяването (то е свързано със скоростта на предаване, вижте илюстрацията по-горе). За COVID-19 се изчислява, че е между 2 и 2,5. Хората, които правят моделите, често пускат своя модел за всяка от възможните стойности, предлагайки диапазон от съответни прогнози.
Заразени, но не болни
Друго важно число, за което в момента много епидемиолози биха искали много да разберат, е броят на истинските случаи на инфекцията сред популацията, който включва броя на случаите на хора, които са имали заболяването, но не са показали някакви симптоми.
„Броят на асимптоматичните е числото, заради което в момента не ме хваща сън. Знаем, че това е изключително важно за нашата стратегия за излизане от епидемията“, коментира Гог.
Това е така, защото има основно две неща, които могат да намалят сегашния експоненциален растеж.
„Първото е, че степента на контактите се променя при мерки като затваряне на училища и физическо дистанциране“, пояснява Гог. "Второто нещо, което променя експоненциалния процес, е изчерпването на податливите на инфекцията хора".
След преболедуването хората придобиват имунитет за известно време и знаейки истинския брой случаи, включително тези без симптоми, може да се разбере колко бързо ще намалее класът на податливите хора. Много обсъжданият механизъм на стадния имунитет означава, че с намаляването на броя на податливите, експоненциалният растеж на болестта се изравнява и след това става експоненциален разпад.
За щастие има надежда, що се отнася до данните за асимптоматиката. Тестове за антитела, които могат да покажат дали един човек е прекарал заболяването, съществуват и сега.
Но дори и при несъвършена информация, моделните прогнози не са удари насляпо, особено ако отчитат и представят диапазона на несигурност. Добрите модели съдържат цялата необходима информация, която имаме. Добрите специалисти по моделиране внимателно следят ограниченията на своите модели и несигурните данни в тях и често включват диапазони от възможни стойности на параметрите, които след това водят до диапазони от прогнози: диапазони от възможни бъдещи сценарии, които могат да възникнат при различни стратегии за интервенция. Прогнозите няма да са перфектни, но те са най-доброто, което можем да направим с информацията, която имаме.
И така, какво ще стане?
Никой не може да каже какво точно ще се случи. Най-голямата надежда - появата на ваксина, още едно средство, чрез което може да бъде изграден стадният имунитет с вариантите за защита на най-уязвимите като приоритет - се очаква след около 12 до 18 месеца. Въпросът е как да стигнем до този момент с най-малко щети.
Едно нещо не се оспорва от никой - ще даваме още дълго време жертви.
„Не можем просто да се затворим за една седмица и да очакваме това нещо да изчезне“, подчертава Гог. „Все още ще е тук (ако мерките за социално дистанциране бъдат отменени твърде скоро] и няма да имаме колективен имунитет. В момента нямаме друг избор, освен да се затворим, за да гарантираме, че здравната ни система няма да е с претоварен капацитет, но сме пределно наясно, че това не може да бъде постоянна стратегия".
Наскоро бе публикувана статия под заглавие "Стратегии за социално дистанциране за ограничаване на епидемията COVID-19" от бившия докторант на Гог, Стивън Кислър (Stephen Kissler) и колегите му в Харвард. Те провеждат задълбочен преглед към проблема за завръщането на епидемията, като се вземат предвид и сезонните колебания - огнищата на заболяванията на дихателната система по-често се проявяват през есента и зимата, което поставя под още по-голямо напрежение здравните системи, тъй като те съвпадат с епидемията от сезонен грип. Кислър и неговият екип използват модела SEIR, който включва компоненти, отразяващи такива сезонни вариации. Ефектът от мерките за социално дистанциране се отразява в модела чрез намаляване на базовото число на репродукция на COVID-19 с до 60%, каквото е наблюдавано и в Китай.
Заключенията от това последно изследване не са съвсем весели. Само един период на социално дистанциране няма да бъде достатъчен, за да се предотврати претоварването на капацитета на леглата за интензивни грижи (проучването разглежда капацитета за САЩ, а не за България, но подобни резултати може да се приложат навсякъде).
"[Според това проучване], се разглеждат периоди на последователни блокировки", разказва Гог. "Идеята е да се въвеждат мерки, когато интензивните отделения са на път да се претоварят. Но във Великобритания Министерството на здравеопазването разширява разпоредбите си, така че да се надяваме, че ограничителните мерки да станат по-кратки и по-малко тежки и не твърде чести".
Колко дълго и често ще се случват тези периоди на социално дистанциране при различни допускания (базирани на данни от САЩ), е показано на графиките по-долу, взети от статията.
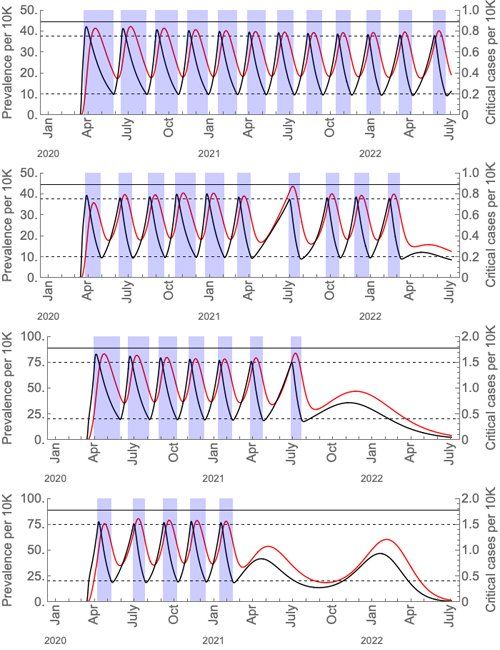
Тези графики показват разпространението на вируса (черните криви) и критичните случаи (червените криви) при периодично социално дистанциране (щтрихованите сини области). Първата и третата графика са без сезонни форсировки; втората и четвъртата със сезонни форсировки. Капацитетът на интензивните отделения е изобразен от плътните хоризонтални черни линии; първите две графики са сценариите с текущия капацитет за интензивни грижи в САЩ, а третата и четвъртата графики са сценариите с удвояване на текущия капацитет за критична помощ. Максималната стойност на базовото число на репродукция е 2 през зимата, а за сезонните сценарии е 1,4 през лятото. Графиките са е от статията Social distancing strategies for curbing the COVID-19 epidemic от Kissler et al.
В цялата тази мрачна картина обаче има няколко лъча надежда. Единият е, че протоколите за терапия и по-добро лечение за тежките случаи на COVID-19 могат да станат реалност в някакъв момент. Това би означавало, че хората ще се разболяват по-малко за по-кратки периоди от време, намалявайки натиска върху здравните системи. Тъй като голяма част от тежестта на мерките за социално дистанциране се свежда до нуждата да предпазим системата на здравеопазване от колапс, така че хората в тежка състояние да могат да бъдат ефективно обгрижвани, това може да означава и по-малко драконични мерки за по-кратки периоди от време.
Другият лъч на надежда е онзи неизвестен общ брой леки и безсимптомни инфекции. Ако те е много по-високо, отколкото се предполага в модела, ако много повече хора са били болни и сега са имунизирани, тогава прогнозите не са никъде близо до толкова лоши, колкото показват цифрите по-горе. Можем само да се надяваме, че това е така. Докато не разберем, всичко, което можем да направим, е да се придържаме към правилата и да останем у дома.
Източник:
How can maths fight a pandemic?, Marianne Freiberger, Plus magazine
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари