

–Į–Ņ–ĺ–Ĺ—Ā–ļ–ł –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł –ĺ–Ņ–ł—Ā–į—Ö–į –Ķ–ī–Ĺ–į –ĺ—ā –Ĺ–į–Ļ-—Ä–į–∑–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ–Ķ–Ĺ–ł—ā–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į¬†- –ľ–ĺ–ī–Ķ–Ľ, –ļ–ĺ–Ļ—ā–ĺ —ā–ĺ—á–Ĺ–ĺ –ĺ–Ņ–ł—Ā–≤–į –ļ–į–ļ —Ä–į—Ā—ā–į—ā –Ľ–ł—Ā—ā–į—ā–į –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į.
‚Äě–†–į–∑—Ä–į–Ī–ĺ—ā–ł—Ö–ľ–Ķ –Ĺ–ĺ–≤–ł—Ź –ľ–ĺ–ī–Ķ–Ľ, –∑–į –ī–į –ĺ–Ī—Ź—Ā–Ĺ–ł–ľ –Ķ–ī–ł–Ĺ —Ā–≤–ĺ–Ķ–ĺ–Ī—Ä–į–∑–Ĺ–į –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā –Ĺ–į —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į. –Ě–ĺ –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā —ā–ĺ–Ļ –Ņ–ĺ-—ā–ĺ—á–Ĺ–ĺ –ĺ—ā—Ä–į–∑—Ź–≤–į –Ĺ–Ķ —Ā–į–ľ–ĺ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į –Ĺ–į –Ķ–ī–Ĺ–ĺ –ļ–ĺ–Ĺ–ļ—Ä–Ķ—ā–Ĺ–ĺ —Ä–į—Ā—ā–Ķ–Ĺ–ł–Ķ, –Ĺ–ĺ –ł –ĺ–Ī—Ö–≤–į—ā–į –Ĺ–į —Ä–į–∑–Ĺ–ĺ–ĺ–Ī—Ä–į–∑–ł–Ķ—ā–ĺ –Ĺ–į –Ņ–ĺ—á—ā–ł –≤—Ā–ł—á–ļ–ł –ľ–ĺ–ī–Ķ–Ľ–ł –Ĺ–į —Ä–į–∑–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į, –Ĺ–į–Ī–Ľ—é–ī–į–≤–į–Ĺ–ł –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į ‚ÄĚ, –∑–į—Ź–≤–ł –ī–ĺ—Ü. –ú—É–Ĺ–Ķ—ā–į–ļ–į –°—É–≥–ł—Ź–ľ–į (Munetaka Sugiyama) –ĺ—ā –Ď–ĺ—ā–į–Ĺ–ł—á–Ķ—Ā–ļ–į—ā–į –≥—Ä–į–ī–ł–Ĺ–į –Ĺ–į –Ę–ĺ–ļ–ł–ĺ.
–õ–ł—Ā—ā–į—ā–į –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į –ĺ—á–į—Ä–ĺ–≤–į—ā —á–ĺ–≤–Ķ—á–Ķ—Ā—ā–≤–ĺ—ā–ĺ –ĺ—ā –Ĺ–Ķ–∑–į–Ņ–ĺ–ľ–Ĺ–Ķ–Ĺ–ł –≤—Ä–Ķ–ľ–Ķ–Ĺ–į. –Ě—Ź–ļ–ĺ–ł, –ļ–į—ā–ĺ —Ā–Ľ—ä–Ĺ—á–ĺ–≥–Ľ–Ķ–ī–į, —Ä–į—Ā—ā–į—ā –≤ –∑–į–Ī–Ķ–Ľ–Ķ–∂–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–į –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź. –Ē—Ä—É–≥–ł –ł–∑–≥–Ľ–Ķ–∂–ī–į—ā –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-—Ö–į–ĺ—ā–ł—á–Ĺ–ł –ł —Ā—Ź–ļ–į—ą –Ĺ–Ķ –Ņ–ĺ–ī–Ľ–Ķ–∂–į—ā –Ĺ–į –Ĺ–ł–ļ–į–ļ–≤–ĺ –ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ. –ė–ľ–į –ī–ĺ—Ä–ł —Ā–Ņ–Ķ—Ü–ł–į–Ľ–Ĺ–ĺ –ł–ľ–Ķ, –ļ–ĺ–Ķ—ā–ĺ –ĺ–Ņ–ł—Ā–≤–į —Ä–į—Ā—ā–Ķ–∂–į –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į: —Ą–ł–Ľ–ĺ—ā–į–ļ—Ā–ł—Ā.
–ē—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ —Ā—ä—Č–ĺ —Ā–į –ĺ—á–į—Ä–ĺ–≤–į–Ĺ–ł –ĺ—ā —ā–Ķ–∑–ł –ľ–ĺ–ī–Ķ–Ľ–ł. –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł –Ķ –Ņ—Ä–į–≤–ł–Ľ –Ĺ–į–Ī–Ľ—é–ī–Ķ–Ĺ–ł—Ź –≤—ä—Ä—Ö—É —Ā–Ņ–ł—Ä–į–Ľ–ĺ–≤–ł–ī–Ĺ–ĺ—ā–ĺ –Ņ–ĺ–ī—Ä–Ķ–∂–ī–į–Ĺ–Ķ –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į, –≤—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ –Ĺ–Ķ –Ķ –ĺ—Ā—ā–į–≤–ł–Ľ —ā–≤—ä—Ä–ī–Ķ –ľ–Ĺ–ĺ–≥–ĺ –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł. –ü–ĺ-–ļ—ä—Ā–Ĺ–ĺ –Ķ—Ā—ā–Ķ—Ā—ā–≤–ĺ–ł–∑–Ņ–ł—ā–į—ā–Ķ–Ľ–ł—ā–Ķ –ĺ—ā–Ī–Ķ–Ľ—Ź–∑–≤–į—ā, —á–Ķ —Ā–Ņ–ł—Ä–į–Ľ–Ĺ–ł—Ź—ā —Ą–ł–Ľ–ĺ—ā–į–ļ—Ā–ł—Ā –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į –Ķ –Ņ–ĺ–Ĺ—Ź–ļ–ĺ–≥–į –Ņ–ĺ –Ņ–ĺ—Ā–ĺ–ļ–į –Ĺ–į —á–į—Ā–ĺ–≤–Ĺ–ł–ļ–ĺ–≤–į—ā–į —Ā—ā—Ä–Ķ–Ľ–ļ–į –ł –ĺ–Ī—Ä–į—ā–Ĺ–ĺ –Ĺ–į —á–į—Ā–ĺ–≤–Ĺ–ł–ļ–ĺ–≤–į—ā–į —Ā—ā—Ä–Ķ–Ľ–ļ–į, –Ĺ–ĺ –ł–∑–≥–Ľ–Ķ–∂–ī–į, —á–Ķ —Ā–Ľ–Ķ–ī–≤–į —ā.–Ĺ–į—Ä.¬†¬†–∑–Ľ–į—ā–Ĺ–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ.
–°—ā–į–Ĺ–į —Ź—Ā–Ĺ–ĺ, —á–Ķ –ľ–Ĺ–ĺ–≥–ĺ —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź —Ā–Ľ–Ķ–ī–≤–į—ā –Ĺ—Ź–ļ–į–ļ–≤–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ —Ä–į–∑–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ, –Ĺ–ĺ –Ĺ–ł–ļ–ĺ–Ļ –Ĺ–Ķ –Ķ —É—Ā–Ņ—Ź–Ľ –ī–į –Ĺ–į–ľ–Ķ—Ä–ł —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ķ–Ĺ –∑–į–ļ–ĺ–Ĺ, –ļ–ĺ–Ļ—ā–ĺ –ī–į –ĺ–Ņ–ł—Ā–≤–į —Ä–į—Ā—ā–Ķ–∂–į –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į.
–ü—Ä–Ķ–∑ 1996 –≥.¬† –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —Ā—ā–ł–≥–Ĺ–į—Ö–į –ľ–Ĺ–ĺ–≥–ĺ –Ī–Ľ–ł–∑–ĺ –ī–ĺ —ā–į–∑–ł —Ü–Ķ–Ľ. –§—Ä–Ķ–Ĺ—Ā–ļ–ł—ā–Ķ¬†—Ą–ł–∑–ł—Ü–ł –°—ā–Ķ—Ą–į–Ĺ –Ē—É–į–ī–ł (Stephane Douady) –ł –ė–≤ –ö—É–ī–Ķ (Yves Couder)¬†—Ä–į–∑—Ä–į–Ī–ĺ—ā–ł—Ö–į –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ, –ļ–ĺ–Ļ—ā–ĺ –Ī–ł –ľ–ĺ–≥—ä–Ľ –ī–į –ĺ–Ī—Ź—Ā–Ĺ–ł –ľ–Ĺ–ĺ–≥–ĺ, –Ĺ–ĺ –Ĺ–Ķ –≤—Ā–ł—á–ļ–ł —Ā—Ö–Ķ–ľ–ł –Ĺ–į –ĺ—Ą–ĺ—Ä–ľ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į. –Ę–ĺ–Ļ —Ā—ā–į–Ĺ–į –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ –ļ–į—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ DC2 –ł –ī–ĺ –ī–Ķ–Ĺ –ī–Ĺ–Ķ—ą–Ķ–Ĺ —Ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į –∑–į –ł–∑–≤–Ķ–∂–ī–į–Ĺ–Ķ –Ĺ–į —Ä–į–∑–Ľ–ł—á–Ĺ–ł –Ņ—Ä–ĺ–ľ–Ķ–Ĺ–Ľ–ł–≤–ł –∑–į —Ą–ł–∑–ł–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į.
 |
–Ę–Ķ–∑–ł –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł —Ā–į –Ĺ–į–Ļ-—Ź—Ā–Ĺ–ĺ –ł–∑—Ä–į–∑–Ķ–Ĺ–ł, –Ī–Ķ–∑ –ĺ—ā–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź, –Ĺ–į –≤—ä—Ä—Ö–į, –Ņ—Ä–ł –Ņ—ä–Ņ–ļ–į—ā–į –Ĺ–į–Ļ-–ĺ—ā–≥–ĺ—Ä–Ķ ‚Äď –ľ–Ķ—Ä–ł—Ā—ā–Ķ–ľ–į ‚Äď –Ĺ–į—Ä–į—Ā—ā–≤–į—Č–ł—Ź –ļ—Ä–į–Ļ –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł–Ķ—ā–ĺ. –Ď–ĺ—ā–į–Ĺ–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł –ļ–į—ā–ĺ –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä –Ľ–ł—Ā—ā–į, –Ľ—é—Ā–Ņ–ł, –Ī–ĺ–ī–Ľ–ł —Ā–Ķ –∑–į—Ä–į–∂–ī–į—ā —ā–į–ľ. –Ě–į —ā–ĺ–∑–ł —Ä–į–Ĺ–Ķ–Ĺ –Ķ—ā–į–Ņ —ā–Ķ —Ā–į —Ā–į–ľ–ĺ –ł–∑–Ņ—ä–ļ–Ĺ–į–Ľ–ĺ—Ā—ā–ł –Ĺ–į –Ī—ä—Ä–∑–ĺ –Ĺ–į—Ä–į—Ā—ā–≤–į—Č–ł –ļ–Ľ–Ķ—ā–ļ–ł, –ł–∑–≤–Ķ—Ā—ā–Ĺ–ł –ļ–į—ā–ĺ –Ņ—Ä–ł–ľ–ĺ—Ä–ī–ł—Ź. |
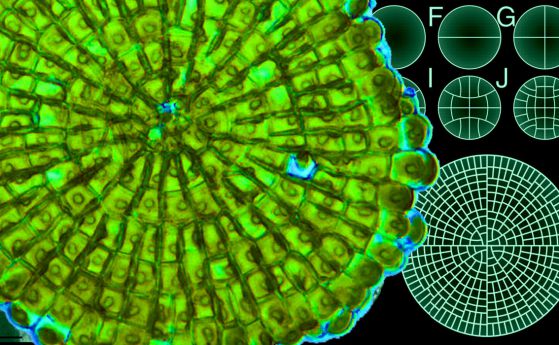
 –°—Ö–Ķ–ľ–į—ā–ł—á–Ĺ–ł –ł–∑–≥–Ľ–Ķ–ī–ł –Ĺ–į –≤—ä—Ä—Ö–į –Ĺ–į —Ą–ł–Ľ–ł–∑–į —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł –≤ DC –ľ–ĺ–ī–Ķ–Ľ–ł. . –ö—Ä–Ķ–ī–ł—ā:¬†Takaaki Yonekura, Akitoshi Iwamoto, Hironori Fujita, Munetaka Sugiyama. 2019. Mathematical model studies of the comprehensive generation of major and minor phyllotactic patterns in plants with a predominant focus on orixate phyllotaxis. PLOS Computational Biology
–°—Ö–Ķ–ľ–į—ā–ł—á–Ĺ–ł –ł–∑–≥–Ľ–Ķ–ī–ł –Ĺ–į –≤—ä—Ä—Ö–į –Ĺ–į —Ą–ł–Ľ–ł–∑–į —Ā –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–ł –≤ DC –ľ–ĺ–ī–Ķ–Ľ–ł. . –ö—Ä–Ķ–ī–ł—ā:¬†Takaaki Yonekura, Akitoshi Iwamoto, Hironori Fujita, Munetaka Sugiyama. 2019. Mathematical model studies of the comprehensive generation of major and minor phyllotactic patterns in plants with a predominant focus on orixate phyllotaxis. PLOS Computational Biology
–°–Ķ–≥–į —Ź–Ņ–ĺ–Ĺ—Ā–ļ–ł—ā–Ķ –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł —Ā–ľ—Ź—ā–į—ā, —á–Ķ —Ā–į –Ĺ–į–ľ–Ķ—Ä–ł–Ľ–ł –ĺ—Č–Ķ –Ņ–ĺ-–ī–ĺ–Ī—Ä–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ, –ļ–ĺ–Ķ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –ĺ–Ī—Ź—Ā–Ĺ–ł –≤—Ā–ł—á–ļ–ł –ľ–ĺ–ī–Ķ–Ľ–ł –≤ —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į.
–Ě–Ķ–Ņ–ĺ–∑–≤–ĺ–Ľ–Ķ–Ĺ–ł –ł–∑–ļ–Ľ—é—á–Ķ–Ĺ–ł—Ź
–Ę–Ķ –∑–į–Ņ–ĺ—á–≤–į—ā –ĺ—ā —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į –ĺ—ā –≤–ł–ī–į¬†Orixa japonica, —Ö—Ä–į—Ā—ā, –ľ–Ķ—Ā—ā–Ķ–Ŭ†–∑–į –Į–Ņ–ĺ–Ĺ–ł—Ź, –ö–ł—ā–į–Ļ –ł –ö–ĺ—Ä–Ķ–Ļ—Ā–ļ–ł—Ź –Ņ–ĺ–Ľ—É–ĺ—Ā—ā—Ä–ĺ–≤. –†–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į –ĺ—ā —ā–ĺ–∑–ł —Ä–ĺ–ī,¬†Orixa, —Ā–į —á–į—Ā—ā –ĺ—ā —É–Ņ–ĺ—Ä–ł—ā–į –≥—Ä—É–Ņ–į, –ļ–ĺ—Ź—ā–ĺ –Ĺ–Ķ —Ā–Ķ –Ņ–ĺ–ī—á–ł–Ĺ—Ź–≤–į –Ĺ–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ DC2. –™–≥–Ľ–ł—ā–Ķ –ľ–Ķ–∂–ī—É –Ľ–ł—Ā—ā–į—ā–į –Ĺ–į O. Japonica —Ā–į –Ņ–ĺ–ī 180 –≥—Ä–į–ī—É—Ā–į, 90 –≥—Ä–į–ī—É—Ā–į, 180 –≥—Ä–į–ī—É—Ā–į, 270 –≥—Ä–į–ī—É—Ā–į, –į —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į —Ā–Ľ–Ķ–ī–≤–į—Č–ł—Ź—ā –Ľ–ł—Ā—ā —Ā–Ķ –≤—Ä—ä—Č–į –ľ–ĺ–ī–Ķ–Ľ–į –Ĺ–į 180 –≥—Ä–į–ī—É—Ā–į.

–õ–ł—Ā—ā–į –Ĺ–į O. japonica –ļ–Ľ–ĺ–Ĺ (–≥–ĺ—Ä–Ķ –≤–Ľ—Ź–≤–ĺ) –ł —Ā—Ö–Ķ–ľ–į—ā–ł—á–Ĺ–į –ī–ł–į–≥—Ä–į–ľ–į –Ĺ–į —Ą–ł–Ľ–ĺ—ā–į–ļ—Ā–ł—Ā–į –ł–ľ (–≤–ī—Ź—Ā–Ĺ–ĺ). –ú–ĺ–ī–Ķ–Ľ—ä—ā –Ĺ–į —ā–ĺ–∑–ł —Ä–ĺ–ī —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ļ–į–∑–≤–į —Ā–Ņ–Ķ—Ü–ł—Ą–ł—á–Ĺ–į —á–Ķ—ā–ł—Ä–ł-—Ü–ł–ļ–Ľ–ł—á–Ĺ–į –Ņ—Ä–ĺ–ľ—Ź–Ĺ–į –Ĺ–į —ä–≥—ä–Ľ–į –ľ–Ķ–∂–ī—É –Ľ–ł—Ā—ā–į—ā–į (180 –≥—Ä–į–ī—É—Ā–į –ī–ĺ 90 –≥—Ä–į–ī—É—Ā–į –ī–ĺ 180 –≥—Ä–į–ī—É—Ā–į –ī–ĺ 270 –≥—Ä–į–ī—É—Ā–į). –ė–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł–Ķ —Ā—ä—Ā —Ā–ļ–į–Ĺ–ł—Ä–į—Č –Ķ–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ķ–Ĺ –ľ–ł–ļ—Ä–ĺ—Ā–ļ–ĺ–Ņ (—Ü–Ķ–Ĺ—ā—ä—Ä –ł –ī–ĺ–Ľ—É –≤–Ľ—Ź–≤–ĺ) –Ņ–ĺ–ļ–į–∑–≤–į –∑–ł–ľ–Ĺ–į –Ņ—ä–Ņ–ļ–į –Ĺ–į Orixa japonica, –≤ –ļ–ĺ—Ź—ā–ĺ –Ľ–ł—Ā—ā–į—ā–į –∑–į–Ņ–ĺ—á–≤–į—ā –ī–į —Ä–į—Ā—ā–į—ā. –ü—Ä–ł–ľ–ĺ—Ä–ī–ł–į–Ľ–Ĺ–ł—ā–Ķ –Ľ–ł—Ā—ā–į —Ā–į –Ķ—ā–ł–ļ–Ķ—ā–ł—Ä–į–Ĺ–ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ —Ā –Ĺ–į–Ļ-—Ā—ā–į—Ä–ł—Ź –Ľ–ł—Ā—ā –ļ–į—ā–ĺ –†8 –ł –Ĺ–į–Ļ-–ľ–Ľ–į–ī–ł—Ź—ā –Ľ–ł—Ā—ā –ļ–į—ā–ĺ –†1. –ö—Ä–Ķ–ī–ł—ā: Takaaki Yonekura, Akitoshi Iwamoto, and Munetaka Sugiyama.
–ü–ĺ–Ĺ–Ķ —á–Ķ—ā–ł—Ä–ł –ī—Ä—É–≥–ł –Ĺ–Ķ—Ā–≤—ä—Ä–∑–į–Ĺ–ł –≥—Ä—É–Ņ–ł —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź —Ā–Ľ–Ķ–ī–≤–į—ā –Ņ–ĺ–ī–ĺ–Ī–Ķ–Ĺ –ľ–ĺ–ī–Ķ–Ľ. –°—É–≥–ł—Ź–ľ–į –ł –ļ–ĺ–Ľ–Ķ–≥–ł—ā–Ķ –ľ—É —Ä–Ķ—ą–į–≤–į—ā –ī–į –Ņ—Ä–ĺ–≤–Ķ—Ä—Ź—ā –ī–į–Ľ–ł –ľ–ĺ–≥–į—ā –ī–į –Ĺ–į–ľ–Ķ—Ä—Ź—ā –ī—Ä—É–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ, —Ā –ļ–ĺ–Ķ—ā–ĺ –ī–į –ĺ–Ņ–ł—ą–į—ā —ā–Ķ–∑–ł —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź, –ļ–į—ā–ĺ —Ā–Ķ –∑–į–Ņ–ĺ—á–Ĺ–Ķ –ĺ—ā —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–ł—ā–Ķ –≥–Ķ–Ĺ–Ķ—ā–ł—á–Ĺ–ł –ł –ļ–Ľ–Ķ—ā—ä—á–Ĺ–ł –ľ–Ķ—Ö–į–Ĺ–ł–∑–ľ–ł, –ļ–ĺ–ł—ā–ĺ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –≤—ä–≤¬† –≤—Ā–ł—á–ļ–ł —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź. –ź–ļ–ĺ —á–Ķ—ā–ł—Ä–ł –ĺ—ā–ī–Ķ–Ľ–Ĺ–ł –≥—Ä—É–Ņ–ł —Ä–į–∑–≤–ł–≤–į—ā –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č –ľ–ĺ–ī–Ķ–Ľ, —ā–ĺ–≥–į–≤–į –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ –ł–ľ–į –Ņ—Ä–ł—á–ł–Ĺ–į –ī–į –Ķ —ā–į–ļ–į. –°–Ľ—É—á–į–Ļ–Ĺ–ĺ –ī–į –Ķ –Ņ–ĺ—Ź–≤–ł –Ĺ–Ķ—Č–ĺ 4 –Ņ—ä—ā–ł –Ķ —ā–≤—ä—Ä–ī–Ķ –ľ–į–Ľ–ļ–ĺ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ, —Ä–į–∑—Ā—ä–∂–ī–į–≤–į—ā –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ.
–Ę–Ķ —ā—Ä—ä–≥–≤–į—ā –ĺ—ā –ī–≤–į—ā–į –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ł –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā—ä–ļ–į –Ĺ–į DC2 —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ:
- –Ď–Ķ–∑ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –ļ–į–ļ–≤–ł –Ņ–į—Ä–į–ľ–Ķ—ā—Ä–ł —Ā–Ķ –Ņ–ĺ—Ā—ā–į–≤—Ź—ā –≤ –Ĺ–Ķ–≥–ĺ, –Ĺ—Ź–ļ–ĺ–ł —Ä–į–∑–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—Ź –Ĺ–į –Ľ–ł—Ā—ā–į –Ĺ–Ķ —Ā–Ķ –ĺ—ā—á–Ķ—ā–į—ā.
- –°–Ņ–ł—Ä–į–Ľ–ĺ–≤–ł–ī–Ĺ–į—ā–į —Ā—Ö–Ķ–ľ–į –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł –Ķ –Ĺ–į–Ļ-—á–Ķ—Ā—ā–ĺ —Ā—Ä–Ķ—Č–į–Ĺ–į—ā–į —Ā–Ņ–ł—Ä–į–Ľ–į, –Ĺ–į–Ī–Ľ—é–ī–į–≤–į–Ĺ–į –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į, –Ĺ–ĺ –Ķ —Ā–į–ľ–ĺ –ľ–į–Ľ–ļ–ĺ –Ņ–ĺ-—á–Ķ—Ā—ā–ĺ —Ā—Ä–Ķ—Č–į–Ĺ–į –ĺ—ā –ī—Ä—É–≥–ł—ā–Ķ —Ā–Ņ–ł—Ä–į–Ľ–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–ł, –ł–∑—á–ł—Ā–Ľ–Ķ–Ĺ–ł —á—Ä–Ķ–∑ DC2 —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ.
–ó–į –ī–į —Ā–Ķ —Ā–Ņ—Ä–į–≤–ł —Ā —ā—Ź—Ö, –Ķ–ļ–ł–Ņ—ä—ā —Ā–Ķ —Ą–ĺ–ļ—É—Ā–ł—Ä–į –≤—ä—Ä—Ö—É –Ķ–ī–Ĺ–ĺ –ļ–Ľ—é—á–ĺ–≤–ĺ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ: —á–Ķ –Ľ–ł—Ā—ā–į—ā–į –Ņ—É—Ā–ļ–į—ā –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ķ–Ĺ —Ā–ł–≥–Ĺ–į–Ľ,¬† –≤—ä–∑–Ņ–ł—Ä–į—Č (–ł–Ĺ—Ö–ł–Ī–ł—Ä–į—Č) —Ä–į—Ā—ā–Ķ–∂–į –Ĺ–į –ī—Ä—É–≥–ł –Ľ–ł—Ā—ā–į –Ĺ–į–Ī–Ľ–ł–∑–ĺ. –Ę–ĺ–≤–į —Ā—ā–į–≤–į, –∑–į—Č–ĺ—ā–ĺ —Ä–į—Ā—ā–Ķ–Ĺ–ł–Ķ—ā–ĺ –ł–ľ–į –Ĺ—É–∂–ī–į –ĺ—ā –Ĺ—Ź–ļ–į–ļ—ä–≤ –Ī–į–Ľ–į–Ĺ—Ā –ł —Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā. –ė–ľ–į –Ĺ—Ź–ļ–ĺ–ł –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–ł—Ź, –ļ–ĺ–ł—ā–ĺ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–į–≥–į—ā, —á–Ķ —ā–ĺ–∑–ł —Ā–ł–≥–Ĺ–į–Ľ —Ā–Ķ —Ä–į–∑–Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ź–≤–į —á—Ä–Ķ–∑ —Ö–ĺ—Ä–ľ–ĺ–Ĺ, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ –į—É–ļ—Ā–ł–Ĺ, –≤—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ —ā–ĺ—á–Ĺ–ł—Ź—ā –ľ–Ķ—Ö–į–Ĺ–ł–∑—ä–ľ –≤—Ā–Ķ –ĺ—Č–Ķ –Ĺ–Ķ –Ķ —Ź—Ā–Ķ–Ĺ.
–°—É–≥–ł—Ź–ľ–į –ĺ—ā—Ö–≤—ä—Ä–Ľ—Ź –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ, —á–Ķ —ā–ĺ–∑–ł —Ā–ł–≥–Ĺ–į–Ľ –Ķ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ķ–Ĺ.
‚Äě–ü—Ä–ĺ–ľ–Ķ–Ĺ–ł—Ö–ľ–Ķ —ā–ĺ–≤–į —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–ĺ –Ņ—Ä–Ķ–ī–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ - –ł–Ĺ—Ö–ł–Ī–ł—Ä–į—Č–į—ā–į —Ā–ł–Ľ–į –Ĺ–Ķ –Ķ –Ņ–ĺ—Ā—ā–ĺ—Ź–Ĺ–Ĺ–į, –į –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź —Ā –≤—ä–∑—Ä–į—Ā—ā—ā–į. –Ę–Ķ—Ā—ā–≤–į—Ö–ľ–Ķ –ļ–į–ļ—ā–ĺ –Ĺ–į—Ä–į—Ā—ā–≤–į—Č–į—ā–į, —ā–į–ļ–į –ł –Ĺ–į–ľ–į–Ľ—Ź–≤–į—Č–į —Ā –≤—ä–∑—Ä–į—Ā—ā—ā–į –ł–Ĺ—Ö–ł–Ī–ł—Ä–į—Č–į —Ā–ł–Ľ–į –ł –≤–ł–ī—Ź—Ö–ľ–Ķ, —á–Ķ —Ā–Ņ–Ķ—Ü–ł—Ą–ł—á–Ĺ–ł—Ź—ā –ľ–ĺ–ī–Ķ–Ľ –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į –ĺ—ā —Ä–ĺ–ī–į Orixa —Ā–Ķ –ł–∑—á–ł—Ā–Ľ—Ź–≤–į –Ņ—Ä–ł –Ņ—Ä–Ķ–ī–Ņ–ĺ—Ā—ā–į–≤–ļ–į—ā–į, —á–Ķ –Ņ–ĺ-—Ā—ā–į—Ä–ł—ā–Ķ –Ľ–ł—Ā—ā–į –ł–ľ–į—ā –Ņ–ĺ-—Ā–ł–Ľ–Ķ–Ĺ –ł–Ĺ—Ö–ł–Ī–ł—ā–ĺ—Ä–Ķ–Ĺ –Ķ—Ą–Ķ–ļ—ā‚ÄĚ, –Ņ–ĺ—Ź—Ā–Ĺ—Ź–≤–į –°—É–≥–ł—Ź–ľ–į.
–° –ī—Ä—É–≥–ł –ī—É–ľ–ł, –ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –Ķ –Ņ–ĺ-—Ā—ā–į—Ä–ĺ –Ľ–ł—Ā—ā–ĺ—ā–ĺ, —ā–ĺ–Ľ–ļ–ĺ–≤–į –Ņ–ĺ-–ľ–į–Ľ–ļ–ĺ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ –Ķ –Ĺ–ĺ–≤–ł—ā–Ķ –Ľ–ł—Ā—ā–į –ī–į —Ä–į—Ā—ā–į—ā –≤ –Ĺ–Ķ–Ņ–ĺ—Ā—Ä–Ķ–ī—Ā—ā–≤–Ķ–Ĺ–į –Ī–Ľ–ł–∑–ĺ—Ā—ā –ī–ĺ –Ĺ–Ķ–≥–ĺ.
–ü–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ—ā–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ –Ĺ–Ķ —Ā–į–ľ–ĺ –ľ–ĺ–∂–Ķ –ī–į –ĺ–Ī—Ź—Ā–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–į –Ĺ–į —Ä–į—Ā—ā–Ķ–∂ –Ĺ–į —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į, –Ĺ–ĺ –ł —Ā–Ķ –≤–Ņ–ł—Ā–≤–į –ľ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ-–ī–ĺ–Ī—Ä–Ķ —Ā –ľ–ĺ–ī–Ķ–Ľ–į, –Ĺ–į–Ī–Ľ—é–ī–į–≤–į–Ĺ –Ņ—Ä–ł –≤—Ā–ł—á–ļ–ł —Ä–į—Ā—ā–Ķ–Ĺ–ł—Ź, —ā–≤—ä—Ä–ī—Ź—ā –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł.
‚Äě–Ě–į—ą–ł—ā–Ķ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–ł—Ź –ł–ľ–į—ā –Ņ–ĺ—ā–Ķ–Ĺ—Ü–ł–į–Ľ–į –Ĺ–į–ł—Ā—ā–ł–Ĺ–į –ī–į —Ä–į–∑–Ī–Ķ—Ä–į—ā –ļ—Ä–į—Ā–ł–≤–ł—ā–Ķ –ľ–ĺ–ī–Ķ–Ľ–ł –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į‚Äú, –ļ–ĺ–ľ–Ķ–Ĺ—ā–ł—Ä–į –°—É–≥–ł—Ź–ľ–į.
–Ě–į–Ļ-—á–Ķ—Ā—ā–ĺ —Ā—Ä–Ķ—Č–į–Ĺ–ł—ā–Ķ —Ā—Ö–Ķ–ľ–ł –Ĺ–į –ĺ—Ą–ĺ—Ä–ľ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ľ–ł—Ā—ā–į —Ā–į –ī–ł—Ā—ā–ł—á–Ĺ–ł (—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ł 180 –≥—Ä–į–ī—É—Ā–į, –Ī–į–ľ–Ī—É–ļ), —Ā–Ņ–ł—Ä–į–Ľ–į –Ĺ–į –§–ł–Ī–ĺ–Ĺ–į—á–ł (—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ł 137,5 –≥—Ä–į–ī—É—Ā–į, —Ā—É–ļ—É–Ľ–Ķ–Ĺ—ā–Ĺ–ĺ—ā–ĺ Graptopetalum paraguayense), –ī–Ķ–ļ—É—Ā–į—ā (—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ł 90 –≥—Ä–į–ī—É—Ā–į, –Ī–ĺ—Ā–ł–Ľ–Ķ–ļ) –ł —ā—Ä–ł–ļ—É—Ā–į—ā (—Ä–į–≤–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ł 60 –≥—Ä–į–ī—É—Ā–į, –ĺ–Ľ–Ķ–į–Ĺ–ī—ä—Ä). –ö—Ä–Ķ–ī–ł—ā: Takaaki Yonekura, Akitoshi Iwamoto, and Munetaka Sugiyama.
–í—Ā–Ķ –ĺ—Č–Ķ –ł —ā–ĺ–∑–ł –ľ–ĺ–ī–Ķ–Ľ –ł–ľ–į –Ĺ—Ź–ļ–ĺ–ł –Ĺ–Ķ–ī–ĺ—Ā—ā–į—ā—ä—Ü–ł - –ľ–į–ļ–į—Ä —á–Ķ –ĺ—ā—á–ł—ā–į –Ņ–ĺ–≤–Ķ—á–Ķ—ā–ĺ –ĺ—ā –ł–∑–ļ–Ľ—é—á–Ķ–Ĺ–ł—Ź—ā–į, –Ĺ–Ķ –ĺ–Ī—Ö–≤–į—Č–į –≤—Ā–ł—á–ļ–ł –ł–∑–ļ–Ľ—é—á–Ķ–Ĺ–ł—Ź.
‚Äě–ė–ľ–į –ł –ī—Ä—É–≥–ł –Ĺ–Ķ–ĺ–Ī–ł—á–į–Ļ–Ĺ–ł –ľ–ĺ–ī–Ķ–Ľ–ł –Ĺ–į —Ä–į–∑–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į, –ļ–ĺ–ł—ā–ĺ –≤—Ā–Ķ –ĺ—Č–Ķ –Ĺ–Ķ —Ā–į –ĺ–Ī—Ź—Ā–Ĺ–Ķ–Ĺ–ł —Ā –Ĺ–į—ą–į—ā–į –Ĺ–ĺ–≤–į —Ą–ĺ—Ä–ľ—É–Ľ–į. –°–Ķ–≥–į —Ā–Ķ –ĺ–Ņ–ł—ā–≤–į–ľ–Ķ –ī–į —Ä–į–∑—Ä–į–Ī–ĺ—ā–ł–ľ –Ĺ–ĺ–≤–į –ļ–ĺ–Ĺ—Ü–Ķ–Ņ—Ü–ł—Ź, –ļ–ĺ—Ź—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –ĺ–Ī—Ź—Ā–Ĺ–ł –≤—Ā–ł—á–ļ–ł –Ņ–ĺ–∑–Ĺ–į—ā–ł –ľ–ĺ–ī–Ķ–Ľ–ł –Ĺ–į –ĺ—Ą–ĺ—Ä–ľ–Ľ–Ķ–Ĺ–ł–Ķ –Ĺ–į –Ľ–ł—Ā—ā–į—ā–į, –į –Ĺ–Ķ —Ā–į–ľ–ĺ –Ņ–ĺ—á—ā–ł –≤—Ā–ł—á–ļ–ł‚ÄĚ, –∑–į—Ź–≤—Ź–≤–į –°—É–≥–ł—Ź–ľ–į.
–ě—Ā—ā–į–≤–į –ī–į —Ā–Ķ –≤–ł–ī–ł –ī–į–Ľ–ł –Ī–ł–ĺ–Ľ–ĺ–∑–ł –ł–Ľ–ł –ī—Ä—É–≥–ł –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł, –ļ–ĺ–ł—ā–ĺ —Ä–į–Ī–ĺ—ā—Ź—ā —Ā —ā–ĺ–≤–į —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ, —Č–Ķ –Ņ–ĺ—ā–≤—ä—Ä–ī—Ź—ā —Ä–Ķ–∑—É–Ľ—ā–į—ā–ł—ā–Ķ –ł —Č–Ķ –≥–ĺ –≤–ļ–Ľ—é—á–į—ā –≤ —Ā–≤–ĺ—Ź—ā–į —Ä–į–Ī–ĺ—ā–į. –ó–į—Ā–Ķ–≥–į –≤—Ä—ä–∑–ļ–į—ā–į –ľ–Ķ–∂–ī—É –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –ł –Ī–ĺ—ā–į–Ĺ–ł–ļ–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ķ —Ā—ā–į–Ĺ–į–Ľ–į –ĺ—Č–Ķ –Ņ–ĺ-–ī—ä–Ľ–Ī–ĺ–ļ–į.
–°–Ņ—Ä–į–≤–ļ–į: Takaaki Yonekura, Akitoshi Iwamoto, Hironori Fujita, Munetaka Sugiyama. 2019. Mathematical model studies of the comprehensive generation of major and minor phyllotactic patterns in plants with a predominant focus on orixate phyllotaxis. PLOS Computational Biology. DOI: 10.1371/journal.pcbi.1007044.
–ė–∑—ā–ĺ—á–Ĺ–ł–ļ:¬†New mathematical model describes the growth pattern of plant leaves
–ě—Č–Ķ –Ņ–ĺ —ā–Ķ–ľ–į—ā–į

–Ę–Ķ—Ö–Ĺ–ĺ–Ľ–ĺ–≥–ł–ł
–ė–∑–ļ—É—Ā—ā–≤–ĺ –ł –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į - –°—ā—ä–ļ–Ľ–Ķ–Ĺ–ł —Ā–ļ—É–Ľ–Ņ—ā—É—Ä–ł –ł –∑–Ľ–į—ā–Ĺ–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ
–Ė–ł–≤–ĺ—ā—ä—ā
–©–Ķ —Ā–Ķ –Ĺ–į–ľ–Ķ—Ä–ł –Ľ–ł –•–ł–≥—Ā –Ī–ĺ–∑–ĺ–Ĺ–į –Ĺ–į –Ī–ł–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į?(–≤–ł–ī–Ķ–ĺ)

–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–†–į—Ā—ā–Ķ–Ĺ–ł—Ź—ā–į - —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ł—Ź—ā –į–Ľ–≥–ĺ—Ä–ł—ā—ä–ľ –Ĺ–į –Ī–ĺ—ā–į–Ĺ–ł–ļ–į—ā–į





















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ
dolivo
–°–į—Ö–į—Ä–į –ĺ—á–į–ļ–≤–į 75% —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–į–Ľ–Ķ–∂–ł—ā–Ķ –ī–ĺ 2100 –≥.