

–Θ–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β―²–Ψ –Ϋ–Α –Φ–Α―¹–Α―²–Α
–û–Ω–Η―²–≤–Α–Ι–Κ–Η ―¹–Β –¥–Α ―¹–Β ―¹―ä–≤–Φ–Β―¹―²–Η –≤―²–Ψ―Ä–Η―è –Ζ–Α–Κ–Ψ–Ϋ –Ϋ–Α –ù―é―²–Ψ–Ϋ ―¹―ä―¹ –Γ–Ω–Β―Ü–Η–Α–Μ–Ϋ–Α―²–Α ―²–Β–Ψ―Ä–Η―è –Ϋ–Α –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ―¹―²―²–Α, –ê–Ι–Ϋ―â–Α–Ι–Ϋ –Ψ―²–Κ―Ä–Η–Μ –¥―Ä―É–≥–Ψ ―¹–Μ–Β–¥―¹―²–≤–Η–Β –Ψ―² ―²–Β–Ψ―Ä–Η―è―²–Α ―¹–Η: –Φ–Α―¹–Α―²–Α –Ϋ–Α –Β–¥–Ϋ–Ψ ―²―è–Μ–Ψ –Ζ–Α–≤–Η―¹–Η –Ψ―² –Ϋ–Β–≥–Ψ–≤–Α―²–Α ―¹–Κ–Ψ―Ä–Ψ―¹―². –€–Α―¹–Α―²–Α –Ϋ–Α –¥–≤–Η–Ε–Β―â–Ψ ―¹–Β ―²―è–Μ–Ψ –Ψ―² –≥–Μ–Β–¥–Ϋ–Α ―²–Ψ―΅–Κ–Α –Ϋ–Α "–Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Β–Ϋ" –Ϋ–Α–±–Μ―é–¥–Α―²–Β–Μ –Β –Ω–Ψ-–≥–Ψ–Μ―è–Φ–Α –≤ ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β ―¹ –Φ–Α―¹–Α―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι –Ϋ–Α ―¹―ä―â–Ψ―²–Ψ ―²―è–Μ–Ψ –Η–Μ–Η –Φ–Α―¹–Α―²–Α, –Κ–Ψ―è―²–Ψ ―²―è–Μ–Ψ―²–Ψ –±–Η –Η–Φ–Α–Μ–Ψ –≤ –Ψ―²–Ω―Ä–Α–≤–Ϋ–Α―²–Α ―¹–Η―¹―²–Β–Φ–Α –Ϋ–Α –Ϋ–Α–±–Μ―é–¥–Α―²–Β–Μ―è.
–†–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Α―²–Α –Φ–Α―¹–Α ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ―è –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α:¬† –Η–Μ–Η m=m0. Έ≥
–ö–Ψ–Μ–Κ–Ψ―²–Ψ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―²―è–Μ–Ψ―²–Ψ –Β –Ω–Ψ-–±–Μ–Η–Ζ–Κ–Α –¥–Ψ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α, ―²–Ψ–Μ–Κ–Ψ–≤–Α –Ω–Ψ-–≥–Ψ–Μ―è–Φ–Α ―¹―²–Α–≤–Α –Φ–Α―¹–Α –Φ―É –Η –Α–Κ–Ψ ―²―è–Μ–Ψ―²–Ψ –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –¥–≤–Η–Ε–Η ―¹―ä―¹ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α, –Φ–Α―¹–Α―²–Α –Φ―É ―â–Β ―¹–Β ―É–≤–Β–Μ–Η―΅–Η –¥–Ψ –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Ψ―¹―². –û―² ―²–Ψ–≤–Α ―¹–Μ–Β–¥–≤–Α, ―΅–Β –Ϋ―è–Φ–Α ―²―è–Μ–Ψ ―¹ –Ϋ–Β–Ϋ―É–Μ–Β–≤–Α –Φ–Α―¹–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι (m0), –Κ–Ψ–Β―²–Ψ –¥–Α ―¹–Β –¥–≤–Η–Ε–Η ―¹―ä―¹ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α, ―²―ä–Ι –Κ–Α―²–Ψ –Ζ–Α ―²–Ψ–≤–Α ―â–Β –Β –Ϋ―É–Ε–Ϋ–Α –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Ψ –≥–Ψ–Μ―è–Φ–Α –Β–Ϋ–Β―Ä–≥–Η―è.
–Λ–Ψ―²–Ψ–Ϋ–Η―²–Β, ―¹–≤–Β―²–Μ–Η–Ϋ–Ϋ–Η―²–Β –Κ–≤–Α–Ϋ―²–Η, ―¹–Α ―΅–Α―¹―²–Η―Ü–Η ―¹ –Ϋ―É–Μ–Β–≤–Α –Φ–Α―¹–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι, ―².–Β. m0=0, –Ζ–Α ―²―è―Ö –Β –Ζ–Α–¥―ä–Μ–Ε–Η―²–Β–Μ–Ϋ–Ψ ¬†–¥–Α ―¹–Β –¥–≤–Η–Ε–Α―² ―¹―ä―¹ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α v=c.
–™–Ψ―Ä–Ϋ–Α―²–Α ―³–Ψ―Ä–Φ―É–Μ–Α –Β –Ω–Ψ―²–≤―ä―Ä–¥–Β–Ϋ–Α –≤ ―Ä–Β–¥–Η―Ü–Α –Β–Κ―¹–Ω–Β―Ä–Η–Φ–Β–Ϋ―²–Η –≤ –Ψ–±–Μ–Α―¹―²―²–Α –Ϋ–Α –Α―²–Ψ–Φ–Ϋ–Α―²–Α ―³–Η–Ζ–Η–Κ–Α. –ü―Ä–Η ―É―¹–Κ–Ψ―Ä―è–≤–Α–Ϋ–Β –Ϋ–Α ―΅–Α―¹―²–Η―Ü–Α¬†(–Β–Μ–Β–Κ―²―Ä–Ψ–Ϋ, –Ω―Ä–Ψ―²–Ψ–Ϋ –Η–Μ–Η –¥―Ä. –Φ–Α―²–Β―Ä–Η–Α–Μ–Ϋ–Α ―΅–Α―¹―²–Η―Ü–Α) –≤ –Κ–Ψ–Μ–Α–Ι–¥–Β―Ä–Η –Β ―É―¹―²–Α–Ϋ–Ψ–≤–Β–Ϋ–Ψ –±―ä―Ä–Ζ–Ψ ―É–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β –Ϋ–Α –Φ–Α―¹–Α―²–Α ―¹ –Ϋ–Α―Ä–Α―¹―²–≤–Α–Ϋ–Β –Ϋ–Α ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ι –Κ–Α―²–Ψ ―²–Ψ–≤–Α ―¹―²–Α–≤–Α ―²–Ψ―΅–Ϋ–Ψ –Ω–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α. ¬†
–€–Α―¹–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι
–Θ–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β―²–Ψ –Ϋ–Α –Φ–Α―¹–Α―²–Α –Ϋ–Β –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α , ―΅–Β ―¹–Β ―É–≤–Β–Μ–Η―΅–Α–≤–Α –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ―²–Ψ –≤–Β―â–Β―¹―²–≤–Ψ, –Η–Ζ–≥―Ä–Α–Ε–¥–Α―â–Ψ ―²―è–Μ–Ψ―²–Ψ –Η–Μ–Η ―΅–Β ―Ä–Β–Α–Μ–Ϋ–Ψ ―¹–Β ―É–≤–Β–Μ–Η―΅–Α–≤–Α―² –Ϋ–Β–≥–Ψ–≤–Η―²–Β ―Ä–Α–Ζ–Φ–Β―Ä–Η. –Δ–Ψ–≤–Α –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α ―¹–Α–Φ–Ψ, ―΅–Β –Ϋ–Α―Ä–Α―¹―²–≤–Α –Η–Ϋ–Β―Ä―²–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α ―²―è–Μ–Ψ―²–Ψ, ―².–Β. –Ζ–Α –¥–Α ―¹–Β –Η–Ζ–Φ–Β–Ϋ–Η ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―²―è–Μ–Ψ―²–Ψ ―â–Β –Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Α –Ω–Ψ-–≥–Ψ–Μ―è–Φ–Α ―¹–Η–Μ–Α, –Ψ―²–Κ–Ψ–Μ–Κ–Ψ―²–Ψ –Α–Κ–Ψ ―²―è–Μ–Ψ―²–Ψ –Β –≤ –Ω–Ψ–Κ–Ψ–Ι ―¹ –Φ–Α―¹–Α m0. –€–Α―¹–Α―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι –Β –≤–Η–Ϋ–Α–≥–Η –Ω–Ψ-–Φ–Α–Μ–Κ–Α m > m0.
–€–Α―¹–Α―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι m0 –Ϋ–Α –Β–¥–Ϋ–Ψ ―²―è–Μ–Ψ –Β –Ω–Ψ―¹―²–Ψ―è–Ϋ–Ϋ–Α –≤–Β–Μ–Η―΅–Η–Ϋ–Α. –ù–Β–Ζ–Α–≤–Η―¹–Η–Φ–Ψ –Κ–Α–Κ–≤–Α ―¹–Κ–Ψ―Ä–Ψ―¹―² –Η–Φ–Α –Β–¥–Ϋ–Ψ ―²―è–Μ–Ψ –≤ –Ω―Ä–Ψ–Η–Ζ–≤–Ψ–Μ–Ϋ–Α –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²–Ϋ–Α ―¹–Η―¹―²–Β–Φ–Α, –≤ ―¹–≤―ä―Ä–Ζ–Α–Ϋ–Α―²–Α ―¹ –Ϋ–Β–≥–Ψ ―¹–Η―¹―²–Β–Φ–Α,¬†―²―è–Μ–Ψ―²–Ψ –Β¬†–≤ –Ω–Ψ–Κ–Ψ–Ι.
–†–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Β–Ϋ –Η–Φ–Ω―É–Μ―¹
| –ê–Κ–Ψ –Β–¥–Ϋ–Α ―΅–Α―¹―²–Η―Ü–Α ―¹–Β –¥–≤–Η–Ε–Η ―¹―ä―¹ ―¹–Κ–Ψ―Ä–Ψ―¹―² v, ―²–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α –Ϋ–Α –Η–Φ–Ω―É–Μ―¹–Α ―¹–Ω–Ψ―Ä–Β–¥ ―²–Β–Ψ―Ä–Η―è―²–Α –Ϋ–Α –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ―¹―²―²–Α ―â–Β –Β:
–ù–Α –≥―Ä–Α―³–Η–Κ–Α―²–Α –≤–¥―è―¹–Ϋ–Ψ ―¹–Α –Ω―Ä–Β–¥―¹―²–Α–≤–Β–Ϋ–Η –Κ–Μ–Α―¹–Η―΅–Β―¹–Κ–Η―è―² –Η ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Η―è―² –Η–Φ–Ω―É–Μ―¹ –≤ –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―² –Ψ―² ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α. –£–Η–Ε–¥–Α ―¹–Β, ―΅–Β –Ω―Ä–Η –Φ–Α–Μ–Κ–Η ―¹–Κ–Ψ―Ä–Ψ―¹―²–Η –¥–≤–Β―²–Β –≥―Ä–Α―³–Η–Κ–Η ―¹―ä–≤–Ω–Α–¥–Α―², –Ϋ–Ψ –Ω―Ä–Η –Ω―Ä–Η–±–Μ–Η–Ε–Α–≤–Α–Ϋ–Β –¥–Ψ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α, –Η–Φ–Ω―É–Μ―¹―ä―² –Κ–Μ–Ψ–Ϋi –Κ―ä–Φ –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Ψ―¹―². –½–Α –¥–Α –Φ–Ψ–Ε–Β ―΅–Α―¹―²–Η―Ü–Α ―¹ –Ϋ–Β–Ϋ―É–Μ–Β–≤–Α –Φ–Α―¹–Α –¥–Α ―¹―²–Η–≥–Ϋ–Β ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α, ―â–Β –Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Α –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è. –ù–Ψ –Ζ–Ϋ–Α―΅–Η―²–Β–Μ–Ϋ–Η –Ψ―²–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η―è –Ψ―² –Κ–Μ–Α―¹–Η―΅–Β―¹–Κ–Η―è –Φ–Ψ–¥–Β–Μ ―¹–Β –Ω―Ä–Ψ―è–≤―è–≤–Α―² ―¹–Α–Φ–Ψ –Ω―Ä–Η ―¹–Κ–Ψ―Ä–Ψ―¹―²–Η, –±–Μ–Η–Ζ–Κ–Η –¥–Ψ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α. –ê–Κ–Ψ ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α v –Β –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ –Ϋ–Η―¹–Κ–Α, –Ψ―²–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η–Β―²–Ψ –Ψ―² –Κ–Μ–Α―¹–Η―΅–Β―¹–Κ–Α―²–Α –¥–Η–Ϋ–Α–Φ–Η–Κ–Α ―¹–Α –Ϋ–Β–Ζ–Ϋ–Α―΅–Η―²–Β–Μ–Ϋ–Ψ - –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä, –Ω―Ä–Η ―¹–Κ–Ψ―Ä–Ψ―¹―² v = c / 4 –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Α―²–Α ―Ä–Α–Ζ–Μ–Η–Κ–Α –Φ–Β–Ε–¥―É –Κ–Μ–Α―¹–Η―΅–Β―¹–Κ–Η―è –Η ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Β–Ϋ –Η–Φ–Ω―É–Μ―¹ –Β ―¹–Α–Φ–Ψ 3%. |
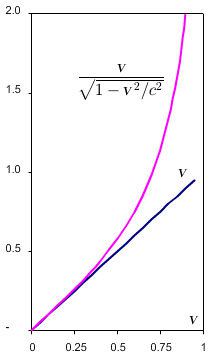 –™―Ä–Α―³–Η–Κ–Α-―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Φ–Β–Ε–¥―É ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Η―è –Η –Ϋ―é―²–Ψ–Ϋ–Ψ–≤–Η―è –Η–Φ–Ω―É–Μ―¹ –Ω―Ä–Η –Φ–Α―¹–Α m = 1 –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è wikipedia. –™―Ä–Α―³–Η–Κ–Α-―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Φ–Β–Ε–¥―É ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Η―è –Η –Ϋ―é―²–Ψ–Ϋ–Ψ–≤–Η―è –Η–Φ–Ω―É–Μ―¹ –Ω―Ä–Η –Φ–Α―¹–Α m = 1 –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è wikipedia. |
–ï–Ϋ–Β―Ä–≥–Η―è―²–Α: E0 = m c2
–ö–Η–Ϋ–Β―²–Η―΅–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è –Β ―Ä–Α–±–Ψ―²–Α―²–Α, –Κ–Ψ―è―²–Ψ ―²―Ä―è–±–≤–Α –¥–Α –Η–Ζ–≤―ä―Ä―à–Η –≤―ä–Ϋ―à–Ϋ–Α ―¹–Η–Μ–Α, –Ζ–Α –¥–Α ―¹–Β ―É―¹–Κ–Ψ―Ä–Η ―²―è–Μ–Ψ –Ψ―² –Ω–Ψ–Κ–Ψ–Ι –¥–Ψ ―¹–Κ–Ψ―Ä–Ψ―¹―² v , –Ϋ–Ψ –Κ–Α–Κ―²–Ψ –≤–Η–¥―è―Ö–Φ–Β –Ω–Ψ-―Ä–Α–Ϋ–Ψ –Φ–Α―¹–Α―²–Α –Β –Ζ–Α–≤–Η―¹–Η –Ψ―² ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Η –Ϋ–Β –Β –Κ–Ψ–Ϋ―¹―²–Α–Ϋ―²–Α. –Δ–Α–Κ–Α –ê–Ι–Ϋ―â–Α–Ι–Ϋ, ―¹–Μ–Β–¥ –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η –Ω―Ä–Β–Ψ–±―Ä–Α–Ζ―É–≤–Α–Ϋ–Η―è, –Η–Ζ–≤–Β–Ε–¥–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α –Ζ–Α –Κ–Η–Ϋ–Β―²–Η―΅–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è –Ϋ–Α –Β–¥–Ϋ–Ψ ―²―è–Μ–Ψ, –¥–≤–Η–Ε–Β―â–Ψ ―¹–Β ―¹ ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Α ―¹–Κ–Ψ―Ä–Ψ―¹―²:
–ö–Ψ–≥–Α―²–Ψ ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α v –Β –Φ–Ϋ–Ψ–≥–Ψ –Ω–Ψ-–Φ–Α–Μ–Κ–Α –Ψ―² ―¹–Κ–Ψ―Ä–Ψ―¹―²―²–Α –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α c (v/c<<1), –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Ι–Κ–Η –ù―é―²–Ψ–Ϋ–Ψ–≤–Η―è –±–Η–Ϋ–Ψ–Φ:
(1 - (v/c)2)1/2 = 1 + 1/2 (v/c)2 + ... βâà 1 + 1/2 (v/c)2
–Η –Ω–Ψ–Μ―É―΅–Α–≤–Α–Φ–Β:
EK¬†βâà m0.c2(1 + 1/2 (v/c)2) - m0¬†c2¬†= 1/2 m0 v 2
–Η ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α –Ω―Ä–Β–Φ–Η–Ϋ–Α–≤–Α –≤―ä–≤ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α –Ζ–Α –Κ–Η–Ϋ–Β―²–Η―΅–Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è –Ψ―² –Κ–Μ–Α―¹–Η―΅–Β―¹–Κ–Α―²–Α –Φ–Β―Ö–Α–Ϋ–Η–Κ–Α: Ek=m0.v2/2 –‰ ―²–Α–Κ–Α, –Ω―Ä–Η –¥–≤–Η–Ε–Β–Ϋ–Η–Β ―¹ ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Η ―¹–Κ–Ψ―Ä–Ψ―¹―²–Η –Κ–Η–Ϋ–Β―²–Η―΅–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è ―¹–Β –Η–Ζ―΅–Η―¹–Μ―è–≤–Α –Κ–Α―²–Ψ ―Ä–Α–Ζ–Μ–Η–Κ–Α―²–Α –Ψ―² –¥–≤–Α ―΅–Μ–Β–Ϋ–Α. –ü―ä―Ä–≤–Η―è―² ―΅–Μ–Β–Ϋ –Β –Ω―ä–Μ–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è –Ϋ–Α ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Α ―΅–Α―¹―²–Η―Ü–Α ―¹ –Φ–Α―¹–Α m, –¥–≤–Η–Ε–Β―â–Α ―¹–Β ―¹―ä―¹ ―¹–Κ–Ψ―Ä–Ψ―¹―² v –Η–Μ–Η:
–ê –≤―²–Ψ―Ä–Η―è―² ―΅–Μ–Β–Ϋ –Β ―².–Ϋ. –Β–Ϋ–Β―Ä–≥–Η―è –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι: ![]() , –Ζ–Ϋ–Α–Φ–Β–Ϋ–Η―²–Α―²–Α ―³–Ψ―Ä–Φ―É–Μ–Α –Ϋ–Α –ê–Ι–Ϋ―â–Α–Ι–Ϋ, –Η–Ζ―Ä–Α–Ζ―è–≤–Α―â–Α –≤―Ä―ä–Ζ–Κ–Α―²–Α –Φ–Β–Ε–¥―É –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Η –Φ–Α―¹–Α―²–Α.
, –Ζ–Ϋ–Α–Φ–Β–Ϋ–Η―²–Α―²–Α ―³–Ψ―Ä–Φ―É–Μ–Α –Ϋ–Α –ê–Ι–Ϋ―â–Α–Ι–Ϋ, –Η–Ζ―Ä–Α–Ζ―è–≤–Α―â–Α –≤―Ä―ä–Ζ–Κ–Α―²–Α –Φ–Β–Ε–¥―É –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Η –Φ–Α―¹–Α―²–Α.
–ü―Ä–Η–Φ–Β―Ä–Η –Ζ–Α –Ω―Ä–Η–Μ–Ψ–Ε–Β–Ϋ–Η–Β –Ϋ–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α¬†E0= mc2
1. –·–¥―Ä–Β–Ϋ ―Ä–Α–Ζ–Ω–Α–¥¬†
–ü–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α E = mc2 –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ–Η –Κ–Ψ–≥–Α –Β –≤―ä–Ζ–Φ–Ψ–Ε–Β–Ϋ ―è–¥―Ä–Β–Ϋ ―Ä–Α–Ζ–Ω–Α–¥, –Κ–Α–Κ―²–Ψ –Η –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ―²–Ψ –Β–Ϋ–Β―Ä–≥–Η―è, –Ψ―²–¥–Β–Μ―è–Ϋ–Α –Ψ―² ―²–Α–Ζ–Η ―Ä–Β–Α–Κ―Ü–Η―è.
–ù–Β–Κ–Α –Η–Φ–Α–Φ–Β –Β–¥–Η–Ϋ –Α―²–Ψ–Φ¬†(–Ϋ–Α–Ω―Ä. ―É―Ä–Α–Ϋ)¬†–≤ –Ω–Ψ–Κ–Ψ–Ι ―¹ –Φ–Α―¹–Α M0. –Δ–Ψ–Ι ―¹–Β ―Ä–Α–Ζ―Ü–Β–Ω–≤–Α –Ϋ–Α –¥–≤–Β ―΅–Α―¹―²–Η ―¹ –Φ–Α―¹–Η¬†m0,1 –Η¬†m0,2. –€–Ψ–Ε–Β–Φ –¥–Α¬†–Ω―Ä–Η–Β–Φ–Β–Φ, ―΅–Β –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Ϋ–Α –≤–Ζ–Α–Η–Φ–Ψ–¥–Β–Ι―¹―²–≤–Η–Β –Φ–Β–Ε–¥―É –¥–≤–Β―²–Β ―΅–Α―¹―²–Η –Β –Ϋ―É–Μ–Β–≤–Α, –Ω―Ä–Η –Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β, ―΅–Β ―¹–Β –Ψ―²–¥–Α–Μ–Β―΅–Α–≤–Α―² –¥–Ψ―¹―²–Α―²―ä―΅–Ϋ–Ψ –Β–¥–Ϋ–Α –Ψ―² –¥―Ä―É–≥–Α. –ê–Κ–Ψ –Β–¥–Ϋ–Α―²–Α ―΅–Α―¹―² –Η–Φ–Α ―¹–Κ–Ψ―Ä–Ψ―¹―² v1, –Α –¥―Ä―É–≥–Α―²–Α - v2, –Α–Κ–Ψ –Ω―Ä–Η–Μ–Ψ–Ε–Β–Φ –Ζ–Α–Κ–Ψ–Ϋ―ä―² –Ζ–Α –Ζ–Α–Ω–Α–Ζ–≤–Α–Ϋ–Β –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Ω―Ä–Β–¥–Η –Η ―¹–Μ–Β–¥ ―Ä–Α–Ζ―Ü–Β–Ω–≤–Α–Ϋ–Β―²–Ψ –Ω–Ψ–Μ―É―΅–Α–≤–Α–Φ–Β:
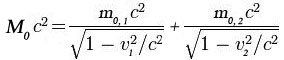
–½–Ϋ–Α–Φ–Β–Ϋ–Α―²–Β–Μ–Η―²–Β –≤ –¥―è―¹–Ϋ–Α―²–Α ―΅–Α―¹―² –Ϋ–Α ―Ä–Α–≤–Β–Ϋ―¹―²–≤–Ψ―²–Ψ –≤–Η–Ϋ–Α–≥–Η ―â–Β ―¹–Α –Ω–Ψ-–Φ–Α–Μ–Κ–Η –Η–Μ–Η ―Ä–Α–≤–Ϋ–Η –Ϋ–Α –Β–¥–Η–Ϋ–Η―Ü–Α –Η –Ζ–Α –¥–Α ―¹–Β ―¹–Ω–Α–Ζ–Η –Ζ–Α–Κ–Ψ–Ϋ―ä―² –Ζ–Α –Ζ–Α–Ω–Α–Ζ–≤–Α–Ϋ–Β –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Β –Ϋ–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Ψ –¥–Α ―¹–Β ―¹–Ω–Α–Ζ–Η –Ϋ–Β―Ä–Α–≤–Β–Ϋ―¹―²–≤–Ψ―²–Ψ:
M0¬†c¬≤¬†βâΞ m0,1c¬≤ +¬†m0,2c¬≤ ¬†
–Η–Μ–Η¬†
M0¬†βâΞ m0,1¬†+¬†m0,2¬† –Ω―Ä–Η –Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β, ―΅–Β v1 = v2 = 0
–î–Β–Μ–Β–Ϋ–Β―²–Ψ –Ϋ–Α ―É―Ä–Α–Ϋ 235 ―¹–Β –Ω–Ψ–¥―΅–Η–Ϋ―è–≤–Α –Ϋ–Α ―¹―ä―â–Ψ―²–Ψ ―É―¹–Μ–Ψ–≤–Η–Β, –Α –Α―²–Ψ–Φ–Ϋ–Α―²–Α –Κ–Η–Ϋ–Β―²–Η―΅–Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è, –Κ–Ψ―è―²–Ψ ―¹–Β –Ψ―²–¥–Β–Μ―è –Β:
–ï–Κ = (M0¬†- m0,1¬†-¬†m0,2 )¬†c¬≤¬†
–ü―ä―Ä–≤–Η―è―², –Κ–Ψ–Ι―²–Ψ –Ψ―¹―ä–Ζ–Ϋ–Α–≤–Α, ―΅–Β ―è–¥―Ä–Ψ―²–Ψ –Ϋ–Α –Β–¥–Η–Ϋ –Α―²–Ψ–Φ –Φ–Ψ–Ε–Β –¥–Α ―¹–Β ―Ä–Α–Ζ―Ü–Β–Ω–Η –Β –Σ―Ä–Ϋ–Β―¹―² –†―ä–¥―ä―Ä―³–Ψ―Ä–¥, –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä ―É―Ä–Α–Ϋ–Ψ–≤–Ψ―²–Ψ ―è–¥―Ä–Ψ ―¹–Β ―Ä–Α–Ζ–¥–Β–Μ―è –Ϋ–Α ―è–¥―Ä–Α―²–Α –Ϋ–Α –±–Α―Ä–Η–Ι –Η –Κ―Ä–Η–Ω―²–Ψ–Ϋ, –Ω―Ä–Η –Κ–Ψ–Β―²–Ψ ―¹–Β –Ψ―²–¥–Β–Μ―è―² –≥–Ψ–Μ―è–Φ–Ψ¬†–Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ –Β–Ϋ–Β―Ä–≥–Η―è, –Α –¦–Η–Ζ–Α –€–Α–Ι―²–Ϋ–Β―Ä –Β –Ω―ä―Ä–≤–Α –Η–Ζ―΅–Η―¹–Μ―è–≤–Α¬†―¹ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α –ê–Ι–Ϋ―â–Α–Ι–Ϋ "–Η–Ζ―΅–Β–Ζ–≤–Α–Ϋ–Β―²–Ψ" –Ϋ–Α –Φ–Α―¹–Α –Ω―Ä–Η ―²–Α–Ζ–Η ―Ä–Β–Α–Κ―Ü–Η―è.
2. –·–¥―Ä–Β–Ϋ ―¹–Η–Ϋ―²–Β–Ζ¬†
–Δ–Ψ–≤–Α –Β –Ψ–±―Ä–Α―²–Ϋ–Η―è –Ω―Ä–Ψ―Ü–Β―¹ –Ϋ–Α –≥–Ψ―Ä–Ϋ–Η―è, –Ω―Ä–Η –Κ–Ψ–Ι―²–Ψ –¥–≤–Α –Α―²–Ψ–Φ–Α ―¹ –Φ–Α―¹–Η¬†m0,1¬†–Η m0,2¬†¬†―¹–Β ―¹–Μ–Η–≤–Α―² –≤ –Β–¥–Η–Ϋ –Α―²–Ψ–Φ ―¹ –Φ–Α―¹–Α M0.
–†–Β–Α–Κ―Ü–Η―è―²–Α –Β –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Α, –Α–Κ–Ψ ―¹–Β –Η–Ζ–Ω―ä–Μ–≤–Α ―É―¹–Μ–Ψ–≤–Η–Β―²–Ψ:
(m0,1¬†+¬†m0,2 )¬†c¬≤ βâΞ¬†M0¬†
–ö–Η–Ϋ–Β―²–Η―΅–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è –Ϋ–Α –Ϋ–Ψ–≤–Ψ–Ψ–±―Ä–Α–Ζ―É–≤–Α–Ϋ–Η―è –Α―²–Ψ–Φ ―â–Β –±―ä–¥–Β:¬†–ï–Κ = (m0,1¬†+ ¬†m0,2 - M0 )¬†c¬≤.
–ü–Ψ–¥–Ψ–±–Ϋ–Η –Ω―Ä–Ψ―Ü–Β―¹–Η ―¹–Α –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Η –Ω―Ä–Η –Η–Ζ–Κ–Μ―é―΅–Η―²–Β–Μ–Ϋ–Ψ –≤–Η―¹–Ψ–Κ–Η ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä–Η –Η¬†―¹–Β –Ϋ–Α―Ä–Η―΅–Α―² ―²–Β―Ä–Φ–Ψ―è–¥―Ä–Β–Ϋ–Η. –Δ–Β ―¹–Β –Η–Ζ–≤―ä―Ä―à–≤–Α―² –≤ –Ζ–≤–Β–Ζ–¥–Η―²–Β (–Η –≤ –Ϋ–Α―à–Β―²–Ψ –Γ–Μ―ä–Ϋ―Ü–Β), –Ω―Ä–Η –Κ–Ψ–Η―²–Ψ ―¹–Β ―¹–Μ–Η–≤–Α―² –¥–Β―É―²–Β―Ä–Η–Ι –Η ―²―Ä–Η―²–Η–Ι –Η ―¹–Β –Ω–Ψ–Μ―É–Α–≤–Α ―Ö–Β–Μ–Η–Ι –Η –Ϋ–Β―É―²―Ä–Ψ–Ϋ.
3. –Θ–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β –Ϋ–Α –Φ–Α―¹–Α―²–Α
–Γ―ä–≥–Μ–Α―¹–Ϋ–Ψ ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α:
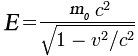 ¬†–Α–Κ–Ψ –≤―¹―è–Κ–Ψ ―É–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –≤–Ψ–¥–Η –¥–Ψ ―É–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β –Ϋ–Α –Φ–Α―¹–Α―²–Α –Φ―É. –ê–Κ–Ψ –Ζ–Α–≥―Ä–Β–Β–Φ, –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä, 1 cm3¬†–≤–Ψ–¥–Α ―¹ –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ ―²–Ψ–Ω–Μ–Η–Ϋ–Α Q , –Ϋ–Η–Β ―â–Β ―É–≤–Β–Μ–Η―΅–Η–Φ –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Φ―É –Η –Ψ―² ―²–Α–Φ - –Φ–Α―¹–Α―²–Α –Φ―É, –Ϋ–Ψ ―²―ä–Ι –Κ–Α―²–Ψ¬†Q ―¹–Β ―Ä–Α–Ζ–¥–Β–Μ―è –Ϋ–Α c, ―É–≤–Β–Μ–Η―΅–Β–Ϋ–Η–Β―²–Ψ –Β –Φ–Ϋ–Ψ–≥–Ψ –Φ–Α–Μ–Κ–Ψ, –Ϋ–Ψ –≤―¹–Β –Ω–Α–Κ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Ψ –Ψ―² –Ϋ―É–Μ–Α. –€–Ψ–Ε–Β –¥–Α ―¹–Β –Η–Ζ―΅–Η―¹–Μ–Η ―¹ –Κ–Ψ–Μ–Κ–Ψ ―â–Β ―¹–Β ―É–≤–Β–Μ–Η―΅–Η –Φ–Α―¹–Α―²–Α –Ϋ–Α –Ϋ–Α¬† 1 cm3 –≤–Ψ–¥–Α, –Α–Κ–Ψ ―¹–Β ―É–≤–Β–Μ–Η―΅–Η ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä–Α―²–Α –Ι –Ψ―² 4–Ψ¬† –¥–Ψ 100–Ψ¬†, ―²–Ψ–≤–Α ―¹–Α¬† ~3.3 .10-12¬†–≥―Ä.
¬†–Α–Κ–Ψ –≤―¹―è–Κ–Ψ ―É–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –≤–Ψ–¥–Η –¥–Ψ ―É–≤–Β–Μ–Η―΅–Α–≤–Α–Ϋ–Β –Ϋ–Α –Φ–Α―¹–Α―²–Α –Φ―É. –ê–Κ–Ψ –Ζ–Α–≥―Ä–Β–Β–Φ, –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä, 1 cm3¬†–≤–Ψ–¥–Α ―¹ –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Ψ ―²–Ψ–Ω–Μ–Η–Ϋ–Α Q , –Ϋ–Η–Β ―â–Β ―É–≤–Β–Μ–Η―΅–Η–Φ –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Φ―É –Η –Ψ―² ―²–Α–Φ - –Φ–Α―¹–Α―²–Α –Φ―É, –Ϋ–Ψ ―²―ä–Ι –Κ–Α―²–Ψ¬†Q ―¹–Β ―Ä–Α–Ζ–¥–Β–Μ―è –Ϋ–Α c, ―É–≤–Β–Μ–Η―΅–Β–Ϋ–Η–Β―²–Ψ –Β –Φ–Ϋ–Ψ–≥–Ψ –Φ–Α–Μ–Κ–Ψ, –Ϋ–Ψ –≤―¹–Β –Ω–Α–Κ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Ψ –Ψ―² –Ϋ―É–Μ–Α. –€–Ψ–Ε–Β –¥–Α ―¹–Β –Η–Ζ―΅–Η―¹–Μ–Η ―¹ –Κ–Ψ–Μ–Κ–Ψ ―â–Β ―¹–Β ―É–≤–Β–Μ–Η―΅–Η –Φ–Α―¹–Α―²–Α –Ϋ–Α –Ϋ–Α¬† 1 cm3 –≤–Ψ–¥–Α, –Α–Κ–Ψ ―¹–Β ―É–≤–Β–Μ–Η―΅–Η ―²–Β–Φ–Ω–Β―Ä–Α―²―É―Ä–Α―²–Α –Ι –Ψ―² 4–Ψ¬† –¥–Ψ 100–Ψ¬†, ―²–Ψ–≤–Α ―¹–Α¬† ~3.3 .10-12¬†–≥―Ä.
4. 
 –‰–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η–Η –Ϋ–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α E = mc2 .¬†–ï–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―² –Ϋ–Α –Φ–Α―¹–Α –Η –Β–Ϋ–Β―Ä–≥–Η―è
–‰–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η–Η –Ϋ–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α E = mc2 .¬†–ï–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―² –Ϋ–Α –Φ–Α―¹–Α –Η –Β–Ϋ–Β―Ä–≥–Η―è
–Δ–Ψ–Ι –Β –Ϋ–Α–Ι-–Η–Ζ–≤–Β―¹―²–Ϋ–Ψ―²–Ψ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –≤ ―¹–≤–Β―²–Α. –ï–¥–≤–Α –Μ–Η –Η–Φ–Α –Ϋ―è–Κ–Ψ–Ι, –Κ–Ψ–Ι―²–Ψ –¥–Α –Ϋ–Β –≥–Ψ –Ζ–Ϋ–Α–Β –Ϋ–Α–Η–Ζ―É―¹―², –Ϋ–Ψ –Ϋ–Β –≤―¹–Β–Κ–Η –≥–Ψ ―Ä–Α–Ζ–±–Η―Ä–Α. –Δ–Ψ –Β –±–Η–Μ–Ψ –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ –¥–Ψ―¹―²–Α –Ω―Ä–Β–¥–Η –Ω―Ä–Ψ–Ζ―Ä–Β–Ϋ–Η―è―²–Α –Ϋ–Α –ê–Ι–Ϋ―â–Α–Ι–Ϋ, –Ϋ–Ψ ―²–Ψ–Ι –≥–Ψ –Η–Ζ–¥–Η–≥–Α¬†–Κ–Α―²–Ψ –≤―¹–Β–Ψ–±―â –Ω―Ä–Η–Ϋ―Ü–Η–Ω.–Δ―ä–Μ–Κ―É–≤–Α–Ϋ–Η―è, ―΅–Β ―²–Ψ –Η–Ζ―Ä–Α–Ζ―è–≤–Α –Ω―Ä–Β–≤―Ä―ä―â–Α–Ϋ–Β―²–Ψ –Ϋ–Α –Φ–Α―²–Β―Ä–Η―è –≤ –Β–Ϋ–Β―Ä–≥–Η―è ―¹–Α –¥–Α–Μ–Β―΅–Β –Ψ―² –Η―¹―²–Η–Ϋ–Α―²–Α, –Ϋ–Α–Ι-–Φ–Α–Μ–Κ–Ψ―²–Ψ, –Ζ–Α―â–Ψ―²–Ψ –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Β ―¹–Α–Φ–Ψ ―¹–≤–Ψ–Ι―¹―²–≤–Ψ –Ϋ–Α –Φ–Α―²–Β―Ä–Η―è―²–Α.
–Δ–Ψ–≤–Α ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Ϋ–Η –Ω–Ψ–Κ–Α–Ζ–≤–Α, ―΅–Β –Φ–Α―¹–Α―²–Α –Η –Β–Ϋ–Β―Ä–≥–Η―è―²–Α ―¹–Α ―¹–≤―ä―Ä–Ζ–Α–Ϋ–Η, –Α –≤ ―Ä–Β–¥–Κ–Η―²–Β ―¹–Μ―É―΅–Α–Η, –Κ–Ψ–≥–Α―²–Ψ –Φ–Α―¹–Α―²–Α ―¹–Β –Ω―Ä–Β–≤―Ä―ä―â–Α –Η–Ζ―Ü―è–Μ–Ψ –≤ –Β–Ϋ–Β―Ä–≥–Η―è, ―¹ ―²–Ψ–≤–Α ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β –Φ–Ψ–Ε–Β –¥–Α –Ω―Ä–Β―¹–Φ–Β―²–Ϋ–Β–Φ –Κ–Ψ–Μ–Κ–Ψ –Β–Ϋ–Β―Ä–≥–Η―è ―â–Β –Ω–Ψ–Μ―É―΅–Η–Φ. –ï–Μ–Β–≥–Α–Ϋ―²–Ϋ–Ψ―¹―²―²–Α, ―¹ –Κ–Ψ―è―²–Ψ ―¹–Α –Ψ–±–Β–¥–Η–Ϋ–Β–Ϋ–Η ―²―Ä–Η –Κ–Ψ―Ä–Β–Ϋ–Ϋ–Ψ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Η ―΅–Α―¹―²–Η –Ϋ–Α –Ω―Ä–Η―Ä–Ψ–¥–Α―²–Α-–Β–Ϋ–Β―Ä–≥–Η―è, ―¹–Κ–Ψ―Ä–Ψ―¹―² –Ϋ–Α ―¹–≤–Β―²–Μ–Η–Ϋ–Α―²–Α –Η –Φ–Α―¹–Α –Β –¥―ä–Μ–±–Ψ–Κ–Α.
–‰–Φ–Α –¥–≤–Α –Ϋ–Α―΅–Η–Ϋ–Α ¬†–Ζ–Α –Η–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η―è –Ϋ–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α E = mc2¬†–≤ –Ζ–Α–≤–Η―¹–Η–Φ–Ψ―¹―² –Ψ―² ―²–Ψ–≤–Α, –Κ–Α–Κ―ä–≤ ―¹–Φ–Η―¹―ä–Μ ―¹–Β –≤–Μ–Α–≥–Α¬†–≤ ―²–Β―Ä–Φ–Η–Ϋ–Η―²–Β "–Φ–Α―¹–Α" –Η "–Β–Ϋ–Β―Ä–≥–Η―è":
- –ê–Κ–Ψ¬†–Φ–Α―¹–Α―²–Α –Ϋ–Α ―²―è–Μ–Ψ―²–Ψ –≤ ―²–Α–Ζ–Η ―³–Ψ―Ä–Φ―É–Μ–Α –Β –Φ–Α―¹–Α―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι, ―²–Ψ ―²–Α–Ζ–Η ―³–Ψ―Ä–Φ―É–Μ–Α –Ϋ–Β –Η–Ζ―Ä–Α–Ζ―è–≤–Α –Ω―ä–Μ–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è, –Α ―¹–Α–Φ–Ψ –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι, ―².–Β. –Ω―Ä–Α–≤–Η–Μ–Ϋ–Η―è―² –Ι –≤–Η–¥ –Β:¬†¬†E0= mc2 –Η –Η–Ζ―Ä–Α–Ζ―è–≤–Α –Φ–Α―¹–Α―²–Α –Ϋ–Α ―²―è–Μ–Ψ―²–Ψ –Κ–Α―²–Ψ¬†–Φ―è―Ä–Κ–Α –Ζ–Α ―¹―ä–¥―ä―Ä–Ε–Α―â–Α―²–Α ―¹–Β –≤ –Ϋ–Β–≥–Ψ –Β–Ϋ–Β―Ä–≥–Η―è. ¬†–Γ–Α–Φ–Η―è―² –ê–Ι–Ϋ―â–Α–Ι–Ϋ –≤¬†–Κ–Ϋ–Η–≥–Α―²–Α ―¹–Η "–Γ―ä―â–Ϋ–Ψ―¹―² –Ϋ–Α ―²–Β–Ψ―Ä–Η―è―²–Α –Ϋ–Α –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ―¹―²―²–Α" (1921–≥.) –Κ–Α–Ζ–≤–Α, ―΅–Β –Η–Ζ–Μ―ä―΅–≤–Α–Ϋ–Β―²–Ψ –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è –≤ ―Ä–Α–¥–Η–Ψ–Α–Κ―²–Η–≤–Ϋ–Η―²–Β ―Ä–Α–Ζ–Ω–Α–¥–Η –Β –Ψ–±―É―¹–Μ–Ψ–≤–Β–Ϋ–Ψ –Ψ―² "–Β–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―²―²–Α –Φ–Β–Ε–¥―É –Φ–Α―¹–Α―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι –Η –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι".¬†
- –û―² –¥―Ä―É–≥–Α ―¹―²―Ä–Α–Ϋ–Α, –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Κ–Α–Ε–Β, ―΅–Β –Ϋ–Α –≤―¹―è–Κ–Α ―³–Ψ―Ä–Φ–Α –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è, –Ϋ–Β ―¹–Α–Φ–Ψ –≤―ä―²―Ä–Β―à–Ϋ–Α―²–Α, –Ϋ–Α –Κ–Ψ–Ι―²–Ψ –Η –¥–Α –Β ―³–Η–Ζ–Η―΅–Β―¹–Κ–Η –Ψ–±–Β–Κ―² ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Α –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Α –Φ–Α―¹–Α. –½–Α―²–Ψ–≤–Α –Ζ–Α –≤―¹―è–Κ–Ψ –¥–≤–Η–Ε–Β―â–Ψ ―¹–Β ―²―è–Μ–Ψ –Φ–Ψ–Ε–Β –¥–Α –≤―ä–≤–Β–¥–Β –Ω–Ψ–Ϋ―è―²–Η–Β―²–Ψ ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Α –Φ–Α―¹–Α, –Κ–Ψ―è―²–Ψ ―É–Φ–Ϋ–Ψ–Ε–Β–Ϋ–Α ―¹ –Κ–Ψ–Β―³–Η―Ü–Η–Β–Ϋ―²–Α c¬≤ –¥–Α–≤–Α –Ω―ä–Μ–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è –Ϋ–Α –Ψ–±–Β–Κ―²–Α. –Δ–Α–Κ–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ϋ–Α–Ω–Η―à–Β –≤―ä–≤ –≤–Η–¥–Α:
E = mrel c¬≤ , –Κ―ä–¥–Β―²–Ψ¬†E –Β¬†–Ω―ä–Μ–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è –Ϋ–Α –Ψ–±–Β–Κ―²–Α, –Α mrel –Β –Ϋ–Β–≥–Ψ–≤–Α―²–Α ―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Α –Φ–Α―¹–Α.
–€–Α–Κ–Α―Ä ―΅–Β –Ω―ä―Ä–≤–Α―²–Α –Η–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η―è –Ϋ–Α –Ω―Ä―ä–≤ –Ω–Ψ–≥–Μ–Β–¥ –Η–Ζ–≥–Μ–Β–Ε–¥–Α ―΅–Α―¹―²–Β–Ϋ ―¹–Μ―É―΅–Α–Ι –Ϋ–Α –≤―²–Ψ―Ä–Α―²–Α: –Β–Ϋ–Β―Ä–≥–Η―è―²–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι –Β ―΅–Α―¹―²–Β–Ϋ ―¹–Μ―É―΅–Α–Ι –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è, –Α m –Β –Ω―Ä–Α–Κ―²–Η―΅–Β―¹–Κ–Η ―Ä–Α–≤–Ϋ–Α –Ϋ–Α mrel –≤ ―¹–Μ―É―΅–Α―è –Ϋ–Α –Ϋ―É–Μ–Β–≤–Α –Η–Μ–Η –Φ–Α–Μ–Κ–Α ―¹–Κ–Ψ―Ä–Ψ―¹―² –Ϋ–Α –¥–≤–Η–Ε–Β–Ϋ–Η–Β ―¹–Ω―Ä―è–Φ–Ψ –Ϋ–Β–≥–Ψ–≤–Α―²–Α –Ψ―²–Ω―Ä–Α–≤–Ϋ–Α ―¹–Η―¹―²–Β–Φ–Α.
–Δ–Α–Κ–Α –Η–Ζ–≥–Μ–Β–Ε–¥–Α, –Ϋ–Ψ –Ϋ–Β –Β ―²–Ψ―΅–Ϋ–Ψ ―²–Α–Κ–Α. –ü–Ψ–Ϋ―è―²–Η–Β―²–Ψ –Φ–Α―¹–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι m –Η–Φ–Α –Ψ―²–¥–Β–Μ–Ϋ–Ψ –Η –≤ –Φ–Ϋ–Ψ–≥–Ψ –Ψ―²–Ϋ–Ψ―à–Β–Ϋ–Η―è –Ω–Ψ-―³―É–Ϋ–¥–Α–Φ–Β–Ϋ―²–Α–Μ–Ϋ–Ψ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –Ψ―² –≤―²–Ψ―Ä–Ψ―²–Ψ ―²―ä–Μ–Κ―É–≤–Α–Ϋ–Β - ―²―è –Β ―¹–Κ–Α–Μ–Α―Ä (―².–Β. –Η–Ζ―Ä–Α–Ζ―è–≤–Α ―¹–Β ―¹ –Β–¥–Ϋ–Ψ ―΅–Η―¹–Μ–Ψ) –Η –Β –Η–Ϋ–≤–Α―Ä–Η–Α–Ϋ―²–Ϋ–Α –≤–Β–Μ–Η―΅–Η–Ϋ–Α, –Κ–Ψ―è―²–Ψ –Ϋ–Β ―¹–Β –Ω―Ä–Ψ–Φ–Β–Ϋ―è, –Κ–Ψ–≥–Α―²–Ψ ―¹–Β ―¹–Φ–Β–Ϋ―è –Ψ―²–Ω―Ä–Α–≤–Ϋ–Α―²–Α ―¹–Η―¹―²–Β–Φ–Α. –û―¹–≤–Β–Ϋ ―²–Ψ–≤–Α –Β –Β–¥–Η–Ϋ―¹―²–≤–Β–Ϋ–Η―è―² ―¹–Κ–Α–Μ–Α―Ä, –Κ–Ψ–Ι―²–Ψ –Ϋ–Β ―¹–Α–Φ–Ψ ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ–Η―Ä–Α –Η–Ϋ–Β―Ä―²–Ϋ–Η―²–Β ―¹–≤–Ψ–Ι―¹―²–≤–Α –Ϋ–Α ―²―è–Μ–Ψ―²–Ψ –Ω―Ä–Η –Ϋ–Η―¹–Κ–Η ―¹–Κ–Ψ―Ä–Ψ―¹―²–Η, –Ϋ–Ψ ―¹―ä―â–Ψ –Η ―΅―Ä–Β–Ζ –Κ–Ψ–Ι―²–Ψ ―²–Β–Ζ–Η ―¹–≤–Ψ–Ι―¹―²–≤–Α –Φ–Ψ–≥–Α―² –Ω―Ä–Ψ―¹―²–Ψ –¥–Α –±―ä–¥–Α―² –Ζ–Α–Ω–Η―¹–Α–Ϋ–Η –Ζ–Α –≤―¹―è–Κ–Α ―¹–Κ–Ψ―Ä–Ψ―¹―² –Ϋ–Α ―²―è–Μ–Ψ―²–Ψ.
–û–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ψ –≤ ―¹―ä–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Α―²–Α ―²–Β–Ψ―Ä–Β―²–Η―΅–Ϋ–Α ―³–Η–Ζ–Η–Κ–Α ―Ä–Α–Ζ–±–Η―Ä–Α–Ϋ–Β―²–Ψ –Ζ–Α –Β–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α –Φ–Α―¹–Α –Η –Β–Ϋ–Β―Ä–≥–Η―è ―¹–Β –Ψ―¹–Ϋ–Ψ–≤–Α–≤–Α –Ϋ–Α –Ω―ä―Ä–≤–Α―²–Α –Η–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η―è, –Ζ–Α―â–Ψ―²–Ψ –≤―²–Ψ―Ä–Α―²–Α –Η–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η―è –Ω―Ä–Β–¥–Η–Ζ–≤–Η–Κ–≤–Α –Ϋ–Β–Ω―Ä–Α–≤–Η–Μ–Ϋ–Ψ―²–Ψ ―²―ä–Μ–Κ―É–≤–Α–Ϋ–Β, ―΅–Β –Φ–Α―¹–Α –Η –Β–Ϋ–Β―Ä–≥–Η―è ―¹–Α –Β–¥–Ϋ–Ψ –Η ―¹―ä―â–Ψ.
–Δ–Α–Κ–Α¬†–Ω–Ψ–Ϋ―è―²–Η–Β―²–Ψ "―Ä–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Α –Φ–Α―¹–Α" –Ω―Ä–Α–Κ―²–Η―΅–Β―¹–Κ–Η –Ϋ–Β ―¹–Β –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α –≤ –Ω―Ä–Ψ―³–Β―¹–Η–Ψ–Ϋ–Α–Μ–Ϋ–Α―²–Α –Μ–Η―²–Β―Ä–Α―²―É―Ä–Α, –Ω–Ψ–¥ –Φ–Α―¹–Α –≤–Η–Ϋ–Α–≥–Η ―¹–Β ―Ä–Α–Ζ–±–Η―Ä–Α –Η–Ϋ–≤–Α―Ä–Η–Α–Ϋ―²–Ϋ–Α―²–Α –Φ–Α―¹–Α.
 –Θ–Μ–Η―Ü–Α –≤ –Δ–Ψ–Κ–Η–Ψ.
–Θ–Μ–Η―Ü–Α –≤ –Δ–Ψ–Κ–Η–Ψ.
–½–Ϋ–Α―΅–Β–Ϋ–Η–Β
–ü―Ä–Β–¥–Η –Ω–Ψ–≤–Β―΅–Β –Ψ―² 100 –≥–Ψ–¥–Η–Ϋ–Η, –ê–Μ–±–Β―Ä―² –ê–Ι–Ϋ―â–Α–Ι–Ϋ –Ω–Ψ―¹―²―É–Μ–Η―Ä–Α ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β―²–Ψ¬†¬†E0= mc2 –≤ ―¹–≤–Ψ―è―²–Α "–Γ–Ω–Β―Ü–Η–Α–Μ–Ϋ–Α ―²–Β–Ψ―Ä–Η―è –Ϋ–Α –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ―¹―²―²–Α." –Θ―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β―²–Ψ –Ω–Ψ–Κ–Α–Ζ–Α –Ϋ–Ψ–≤ –Ϋ–Α―΅–Η–Ϋ –Ζ–Α –Ψ–Ω–Η―¹–Α–Ϋ–Η–Β –Ϋ–Α –Ω―Ä–Ψ–Η–Ζ―Ö–Ψ–¥–Α –Ϋ–Α ―Ö–Η–Φ–Η―΅–Β―¹–Κ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è –Η –Ω―Ä–Β–¥–Μ–Ψ–Ε–Η –¥―Ä―É–≥ –Η–Ζ―²–Ψ―΅–Ϋ–Η–Κ –Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è, –Η–Ζ–≤–Β―¹―²–Β–Ϋ –¥–Ψ―¹–Β–≥–Α –≤ –Η―¹―²–Ψ―Ä–Η―è―²–Α - ―è–¥―Ä–Β–Ϋ–Α―²–Α –Β–Ϋ–Β―Ä–≥–Η―è. –Δ―è –≤–Μ–Β–Ζ–Β –≤ –Η―¹―²–Ψ―Ä–Η―è―²–Α ―΅–Β―²–Η―Ä–Β–¥–Β―¹–Β―² –≥–Ψ–¥–Η–Ϋ–Η –Κ―ä―¹–Ϋ–Ψ –Ω–Ψ –Β–¥–Η–Ϋ ―É–Ε–Α―¹―è–≤–Α―â –Ϋ–Α―΅–Η–Ϋ - –Ω–Ψ–¥ ―³–Ψ―Ä–Φ–Α―²–Α –Ϋ–Α –Α―²–Ψ–Φ–Ϋ–Α –±–Ψ–Φ–±–Α. –ù–Ψ –≤―¹–Β –Ω–Α–Κ ―É―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α –ê–Ι–Ϋ―â–Α–Ι–Ϋ –Ϋ–Η ―Ä–Α–Ζ–Κ―Ä–Η –Η –Β–¥–Ϋ–Α –Ϋ–Ψ–≤ –Η–Ζ―²–Ψ―΅–Ϋ–Η–Κ –Ϋ–Α –Ω–Ψ―΅―²–Η –Ϋ–Β–Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η –Κ–Ψ–Μ–Η―΅–Β―¹―²–≤–Α –Β–Ϋ–Β―Ä–≥–Η―è ―¹ –Ω―Ä–Β–Ϋ–Β–±―Ä–Β–Ε–Η–Φ–Ψ –Φ–Α–Μ―ä–Κ –Β―³–Β–Κ―² –≤―ä―Ä―Ö―É –Ψ–Κ–Ψ–Μ–Ϋ–Α―²–Α ―¹―Ä–Β–¥–Α.
–û―¹–Ϋ–Ψ–≤–Ϋ–Η –Ω–Ψ–Ϋ―è―²–Η―è –Η –Μ–Β–Κ―¹–Η–Κ–Α:
- –†–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Ϋ–Α –Φ–Α―¹–Α
- –€–Α―¹–Α –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι
- –†–Β–Μ–Α―²–Η–≤–Η―¹―²–Η―΅–Β–Ϋ –Η–Φ–Ω―É–Μ―¹
- –ü―ä–Μ–Ϋ–Α –Β–Ϋ–Β―Ä–≥–Η―è
- –ï–Ϋ–Β―Ä–≥–Η―è –Ϋ–Α –Ω–Ψ–Κ–Ψ–Ι
- –Λ–Ψ―Ä–Φ―É–Μ–Α―²–Α: E0 = m c2
- –·–¥―Ä–Β–Ϋ ―Ä–Α–Ζ–Ω–Α–¥
- –·–¥―Ä–Β–Ϋ ―¹–Η–Ϋ―²–Β–Ζ
- –ê–Μ–±–Β―Ä―² –ê–Ι–Ϋ―â–Α–Ι–Ϋ
–‰–Ζ―²–Ψ―΅–Ϋ–Η―Ü–Η:
–Δ–Β–Ψ―Ä–Η―è –Ϋ–Α –ê–Ι–Ϋ―â–Α–Ι–Ϋ, –î–Ψ―΅–Ψ –™. –Λ–Α–Κ–Η―Ä–Ψ–≤, –Γ–Ψ―³–Η―è, 1961–≥, –î–‰ "–ù–Α―Ä–Ψ–¥–Ϋ–Α –Ω―Ä–Ψ―¹–≤–Β―²–Α"
–Λ–û–†–€–Θ–¦–ê–Δ–ê –ù–ê –ê–ô–ù–©–ê–ô–ù: –ï0 = mc2¬†βÄû–ù–Β –Ϋ–Η –Μ–Η ―¹–Β –Ϋ–Α–¥―¹–Φ–Η–≤–Α –™–Ψ―¹–Ω–Ψ–¥ –ë–Ψ–≥βÄù?,¬†–¦. –ë. –û–Κ―É–Ϋ (pdf)
–≠–ö–£–‰–£–ê–¦–ï–ù–Δ–ù–Ϊ –¦–‰ –€–ê–Γ–Γ–ê –‰ –≠–ù–ï–†–™–‰–·? ,¬†–£.–ê. –≠―²–Κ–Η–Ϋ¬†(pdf)
–½–Α–Κ–Ψ–Ϋ ―ç–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―²–Η –Φ–Α―¹―¹―΄ –Η ―ç–Ϋ–Β―Ä–≥–Η–Η
–≠–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―²―¨ –Φ–Α―¹―¹―΄ –Η ―ç–Ϋ–Β―Ä–≥–Η–Η



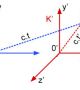

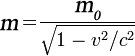
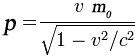
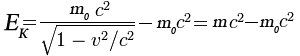
 –‰–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η–Η –Ϋ–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α E = mc2 .¬†–ï–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―² –Ϋ–Α –Φ–Α―¹–Α –Η –Β–Ϋ–Β―Ä–≥–Η―è
–‰–Ϋ―²–Β―Ä–Ω―Ä–Β―²–Α―Ü–Η–Η –Ϋ–Α ―³–Ψ―Ä–Φ―É–Μ–Α―²–Α E = mc2 .¬†–ï–Κ–≤–Η–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―² –Ϋ–Α –Φ–Α―¹–Α –Η –Β–Ϋ–Β―Ä–≥–Η―è













–ö–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
–€–Ψ–Μ―è, ―Ä–Β–≥–Η―¹―²―Ä–Η―Ä–Α–Ι―²–Β ―¹–Β –Ψ―² T–Θ–ö!
–ê–Κ–Ψ –≤–Β―΅–Β –Η–Φ–Α―²–Β ―Ä–Β–≥–Η―¹―²―Ä–Α―Ü–Η―è, –Ϋ–Α―²–Η―¹–Ϋ–Β―²–Β –Δ–Θ–ö!
–ù―è–Φ–Α –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η –Κ―ä–Φ ―²–Α–Ζ–Η –Ϋ–Ψ–≤–Η–Ϋ–Α !
–ü–Ψ―¹–Μ–Β–¥–Ϋ–Η –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
Gunteer
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
–Ξ―Ä–Η―¹―²–Η―è–Ϋ–Η–Ϋ
–Δ–Ψ–≤–Α –Β –Κ―Ä–Α–Μ―è―² –Ϋ–Α ―²–Η–Κ–≤–Η―²–Β: –Δ–Η–Κ–≤–Α―²–Α –Φ―É ―²–Β–Ε–Η –Ϋ–Α–¥ –Β–¥–Η–Ϋ –Β–¥–Η–Ϋ ―²–Ψ–Ϋ
dolivo
–Γ–Α―Ö–Α―Ä–Α –Ψ―΅–Α–Κ–≤–Α 75% ―É–≤–Β–Μ–Η―΅–Β–Ϋ–Η–Β –Ϋ–Α –≤–Α–Μ–Β–Ε–Η―²–Β –¥–Ψ 2100 –≥.
dolivo
–½–Β–Φ–Ϋ–Α―²–Α ―è–±―ä–Μ–Κ–Α: ―¹―²–Α―Ä–Α –Κ―É–Μ―²―É―Ä–Α –Ζ–Α –Ϋ–Ψ–≤–Η―²–Β –Κ–Μ–Η–Φ–Α―²–Η―΅–Ϋ–Η –≤―Ä–Β–Φ–Β–Ϋ–Α