Странна нова фаза на материята, заемаща две времеви измерения едновременно

Чрез осветяване на атоми в квантов компютър с лазерни импулси, вдъхновени от числата на Фибоначи, физиците са създали забележителна, невиждана досега фаза на материята. Фазата има предимствата на две времеви измерения, въпреки че все още има само един единствен времеви поток, съобщават физици в Nature.

Това главозамайващо свойство предлага търсено предимство: информацията, съхранявана във фазата, е много по-защитена от грешки, отколкото при алтернативните конфигурации, използвани понастоящем в квантовите компютри. В резултат на това информацията може да съществува, без да се изкривява, много по-дълго, което е важен етап за превръщането на квантовите компютри в жизнеспособни, казва водещият автор на изследването Филип Думитреску (Philipp Dumitrescu).

Използването на "допълнително" измерение на времето в подхода "е напълно различен начин на мислене за фазите на материята", заявява Думитреску, който е работил по проекта като научен сътрудник в Центъра за компютърна квантова физика към Института "Флатирон" в Ню Йорк. "Работя върху тези теоретични идеи повече от пет години и да видя как те се реализират в експерименти е вълнуващо."

Експериментите са проведени на квантов компютър в Quantinuum в Брумфийлд, Колорадо.

Основните двигатели на квантовия компютър на екипа са 10 атомни йона на елемент, наречен итербий. Всеки йон се държи и контролира индивидуално от електрическите полета, създадени от йонен капан, и може да се манипулира или измерва с помощта на лазерни импулси.

Всеки от тези атомни йони служи за това, което учените наричат квантов бит или "кубит". Докато традиционните компютри измерват информацията в битове (всеки от които представлява 0 или 1), кубитите, използвани от квантовите компютри, използват странностите на квантовата механика, за да съхраняват още повече информация. Точно както котката на Шрьодингер е едновременно жива и мъртва в кутията си, един кубит може да бъде 0, 1 или смесица - или "суперпозиция" - от двете. Тази допълнителна плътност на информацията и начинът, по който кубитите взаимодействат помежду си, обещават да позволят на квантовите компютри да се справят с изчислителни проблеми, които са далеч отвъд възможностите на конвенционалните компютри.

Има обаче голям проблем: Точно както надникването в кутията на Шрьодингер предопределя съдбата на котката, така и взаимодействието с кубита. И дори не е необходимо това взаимодействие да е умишлено. "Дори ако държите всички атоми под строг контрол, те могат да загубят квантовите си свойства, докато контактуват с околната среда, нагряват се или взаимодействат с неща по начин, който не сте планирали", отбелязва Думитреску. "На практика експерименталните устройства имат много източници на грешки, които могат да влошат кохерентността само след няколко лазерни импулса."

Затова задачата е да се направят кубитите по-устойчиви. За целта физиците могат да използват "симетрии", по същество свойства, които издържат на промени. (Снежинката например има ротационна симетрия, защото изглежда по един и същи начин, когато се завърти на 60 градуса.) Един от методите е добавянето на времева симетрия чрез облъчване на атомите с ритмични лазерни импулси. Този подход помага, но Думитреску и неговите сътрудници се питат дали могат да отидат по-далеч. Затова вместо само една времева симетрия те се стремят да добавят две, като използват подредени, но неповтарящи се лазерни импулси.

В този квантов компютър физиците създават невиждана досега фаза на материята, която действа така, сякаш времето има две измерения. Фазата би могла да помогне за защита на квантовата информация от разрушаване за много по-дълъг период от сегашните методи. Кредит: Quantinuum

Най-добрият начин да разберем техния подход е като разгледаме нещо друго подредено, но неповтарящо се: " квазикристалите." Типичният кристал има редовна, повтаряща се структура, като шестоъгълниците в пчелна пита. Квазикристалът все още е подреден, но неговите модели никога не се повтарят. (Още по-удивително е, че квазикристалите са кристали от по-високи измерения, проектирани или смалени в по-ниски измерения. Тези по-високи измерения могат да бъдат дори извън трите измерения на физическото пространство: Например двуизмерната мозайка на Пенроуз е проектирано парче от 5-измерна решетка.

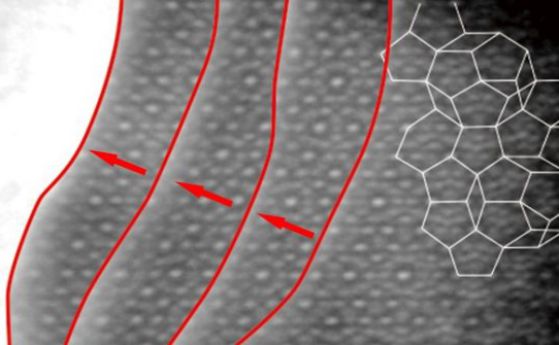
Атомен модел на повърхността на квазикристал (Al-Pd-Mn).  Кредит: Wikimedia Commons

За кубитите Думитреску и екипът му предлагат през 2018 г. създаването на квазикристал във времето, а не в пространството. Докато периодичен лазерен импулс би се редувал (A, B, A, B, A, B и т.н.), изследователите създават квазипериодичен режим на лазерните импулси, основан на последователността на Фибоначи. В тази последователност всяка част от последователността е сума от двете предишни части (A, AB, ABA, ABAAB, ABAABABA и т.н.). Тази подредба, подобно на квазикристала, е подредена, без да се повтаря. И подобно на квазикристала, това е двуизмерен модел, смачкан в едно измерение. Това сплескване на измеренията теоретично води до две времеви симетрии вместо само една: Системата по същество получава допълнителна симетрия от несъществуващо допълнително измерение на времето.

Реалните квантови компютри обаче са невероятно сложни експериментални системи, така че остава недоказано дали обещаните от теорията предимства ще се запазят в реалните кубити.

Използвайки квантовия компютър Quantinuum, експериментаторите подлагат теорията на проверка. Те подават лазерна светлина към кубитите на компютъра както периодично, така и чрез последователност, основана на числата на Фибоначи. Фокусът е бил върху кубитите в двата края на 10-атомната композиция. Именно там изследователите са очаквали да видят новата фаза на материята, изпитваща едновременно две времеви симетрии. При периодичния тест крайните кюбити остават квантови за около 1,5 секунди - вече впечатляваща продължителност, като се има предвид, че кубитите взаимодействат силно помежду си. При квазипериодичния модел кюбитите остават квантови за цялата продължителност на експеримента - около 5,5 секунди. Това е така, защото допълнителната времева симетрия осигурява по-голяма защита, смята Думитреску.

Реалните квантови компютри обаче са невероятно сложни експериментални системи, така че остава недоказано дали обещаните от теорията предимства ще се запазят в реалните кубити.

"При тази квазипериодична последователност има сложна еволюция, която анулира всички грешки, които живеят на ръба", разказва той. "Поради това ръбът остава квантово-механично кохерентен много, много по-дълго, отколкото бихте очаквали."

Въпреки че откритията показват, че новата фаза на материята може да действа като дългосрочна памет за квантова информация, изследователите все още трябва да интегрират функционално фазата с изчислителната страна на квантовите изчисления. "Имаме това директно, съблазнително приложение, но трябва да намерим начин да го вкараме в изчисленията", казва Думитреску. "Това е нерешен проблем, по който работим."

Справка: Philipp Dumitrescu, Dynamical topological phase realized in a trapped-ion quantum simulator, Nature (2022). DOI: 10.1038/s41586-022-04853-4. www.nature.com/articles/s41586-022-04853-4

Източник: Strange new phase of matter created in quantum computer acts like it has two time dimensions, Simons Foundation

Опити за обяснение за съществуването на квазикристали

Известно е, че при кристалите се наблюдава осева симетрия само от 1, 2, 3, 4 и 6-ти ред, съответно те съвпадат при завъртане на 180°, 120°, 90° и 60°. Няма кристални решетки със симетрия от 5-ти ред и над шести ред.

Но вече е признато съществуването и на квазикристали с пространствена решетка по законоверностите на мозайките на Пенроуз -  подредена, но никога не се повтаря. 

Да се обясни растежа и стабилността на квазикристалите е невъзможно със средствата на класическата кристалография. Липсва транслация, но как се обясняват белезите на все пак някаква подреденост?

Установено е, че съотношението на елементите на квазикристалите е в златна пропорция, което съчетано с петоъгълната симетрия натрапва приликата с "мозайките на Пенроуз" и както казва Питър Дж. Лу, от Харвардския университет като че ли ислямските математици и художници са открили схемата на квазикристалите преди стотици години.

Атомен модел на повърхността на квазикристал (Al-Pd-Mn).Снимка: wikipedia

Мозайка на нобеловия лауреат Пенроуз "двата ромба". Илюстрация: quadibloc.com

Фрагмент от средновековна ислямска мозайка, Исфахан, Иран. Снимка: math.ucr.edu

 Обемна мозайка на Пенроуз. Снимка: Livejournal

Въпреки, че непериодичните мозайки на Пенроуз са се появили като математическа игра, те са впрегнати да обяснят това ново явление. Тази теория приложил към кристалографията Алън Маккей. Той поставил атоми във възлите на мозайката на Пенроуз, изчислява картината на дифракция и получава модел със симетрия от десети ред, подобен на квазикристалните.

_{Фрагменти на атомната структура на квазикристалите могат да бъдат тримерни аналози на мозайките на Пенроуз - остри и тъпи ромбоедри с ъгли при върховете 63,43° и 116,57°, из които може да се сглоби многостен, наречен триаконтаедър със симетрия 53m.}

В обемния си вариант мозайката на Пенроуз може да е съставена от икосаедри - дванайсетостени с триъгълни стени, като на всеки връх се срещат пет триъгълници, от където идва и симетрията от 5-ти порядък.

Проекция от 6-тото измерение

Преди да продължим, ви препоръчвам да прегледате раздел Четвъртото измерение в този сайт, ако досега не сте се сблъсквали с идеята за пространства с размерност над обичайната ни.

Тъй като да се опишат квазикристалите в 3D пространството не е толкова лесно, колкото при нормални кристални структури, на помощ ни идват и по-висшите пространства.

За да се определят нормалните кристали са достатъчни три цели числа (индекси на Милер), отразяващи триизмерната транслационна периодичност на структурата.

Необходимостта от n вектора съответства на nD-мерно пространство. С други думи, в пространство с по-висока размерност от трета, квазикристалите може да се опишат периодично.

Ще си обясним това с пример от една по-ниска размерност. Представете си една двумерна периодична решетка Да прекараме ос и проектираме върху нея точките, които попадат в ивицата около оста. Ако наклонът й някаква част от периода, да речем 1/2, то проекциите ще отразяват периодичната структура на двумерната решетка.

 

Но ако наклонът е някакво ирационално число като π (3.1415...) или златното сечение φ=1.618... - често срещано при кристалите, тогава проекциите ще са една непериодична едномерна решетка. Последователността на тези стойности изглежда повече или по-малко хаотична - липсва транслационна симетрия, ако не разширим пространството до две измерения, тогава всичко става ясно: нашият едномерен квазикристал е само част от проекцията на една периодична квадратна мрежа.

И така, за да се зададат целочислени индекси на квазикристалите са необходими най-малко 5 линейно независими вектори за многоъгълните квазикристали и 6 за икосаедрични квазикристали.

Тоест необходимо е пет- или шестмерно пространство, в което квазикристалите са периодични. При проекция в тримерното пространство периодичността изчезва и се превръща в необичайната петоъгълно-симетрична дифракционна картина.

Истинската квазипериодична структура в 3D-физическото пространство може да бъде получена чрез подходящи техники за проекция и сечение. Така че е достатъчно да се определи една единична клетка с nD-структура, чието съдържание се състои от "хиператоми", по аналогия на атомите в една нормална единична клетка в кристалите. Това ни позволява да се опише цялата структура на квазикристалите с ограничен набор от параметри.

Оказва се, че картината на мозайката на Пенроуз при квазикристалите се получава като сечение на пет- и шестмерна кубична решетка с наклонена равнина.

Не всички приемат това толкова сложно обяснение - то обяснява дифракционната картина, но не дава отговор на въпроса как локалните междуатомни взаимодействия може да стабилизират квазикристала и установят периодичност на далечни разстояния в едно хиперпространство.

В същото време, при растежа на кристала от стопилката, атомите се присъединяват към повърхността на зародиша по някакъв закон, който има локален характер. Как атомите "знаят" (заради естеството на междуатомните си взаимодействия) какви местната конфигурации може да образуват и какви не може за да се формира в двумерния случай мозайка на Пенроуз.

Някои смятат, че квазикристалът е всъщност микрокристално състояние, при което веществото се групира в икосаедрични клъстери, произволно свързани помежду си, а кристалографски ограничения върху такива опаковки няма, защото клъстерът може да има каквато и да е форма - той няма нужда да запълва с решетката си безкрайни пространства. Въпросът остава открит.

Още по темата

10/09/2018

Физика

Изненадващ скрит ред обединява простите числа и квазикристалите

17/08/2016

Физика

Учени обясняват математически квазикристалната структура

20/08/2015

Физика

За първи път показаха как растат квазикристалите (видео)

03/04/2015

Математика

Квазикристалите - между два свята