

–£—З–µ–љ–Є –Њ—В –Т–µ–ї–Є–Ї–Њ–±—А–Є—В–∞–љ–Є—П –Є –°–Р–© –і–∞–і–Њ—Е–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ –Њ–±—П—Б–љ–µ–љ–Є–µ –љ–∞ –љ–µ–њ–µ—А–Є–Њ–і–Є—З–љ–Є –Љ–Њ–Ј–∞–є–Ї–Є –≤ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ. –Т—К–Ј –Њ—Б–љ–Њ–≤–∞ –љ–∞ —Б–≤–Њ–Є—В–µ –Є–Ј—З–Є—Б–ї–µ–љ–Є—П, —В–µ –њ–Њ—Б—В—А–Њ—П–≤–∞—В 3D –Љ–Њ–і–µ–ї –љ–∞¬†–Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї —Б—К—Б —Б–Є–Љ–µ—В—А–Є—П –Њ—В 5-—В–Є —А–µ–і, —А–∞–Ј–Ї–∞–Ј–≤–∞ —Б–∞–є—В—К—В The Conversation.
–Ш–Ј—Б–ї–µ–і–≤–∞–љ–µ—В–Њ –Є–Љ –µ –њ—Г–±–ї–Є–Ї—Г–≤–∞–љ–Њ –≤ —Б–њ–Є—Б–∞–љ–Є–µ Physical Review Letters.
–Э–∞–є-–і–Њ–±—А–∞—В–∞ –Њ–њ–∞–Ї–Њ–≤–Ї–∞ –љ–∞ –∞—В–Њ–Љ–Є—В–µ –≤ –Ї—А–Є—Б—В–∞–ї–∞ —Б–µ –њ–Њ–і—З–Є–љ—П–≤–∞ –љ–∞ –Ј–∞–Ї–Њ–љ–Є—В–µ –љ–∞ —Б–Є–Љ–µ—В—А–Є—П—В–∞, –Ј–∞—Й–Њ—В–Њ —В—П –µ –µ–љ–µ—А–≥–Є–є–љ–Њ –љ–∞–є-–±–ї–∞–≥–Њ–њ—А–Є—П—В–љ–∞ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ —Б—В—А—Г–Ї—В—Г—А–Є. –Ь–Њ–ґ–µ –љ–∞–є-–і–Њ–±—А–µ –і–∞ —Б–Є –≥–Њ –њ—А–µ–і—Б—В–∞–≤–Є–Љ –Ї–∞—В–Њ –њ–ї–Њ—З–љ–Є–Ї –Є–ї–Є –њ–∞—А–Ї–µ—В. –Э–Њ –≤ –њ—А–Є—А–Њ–і–∞—В–∞ –Є–Љ–∞ –Є –љ–µ–њ–µ—А–Є–Њ–і–Є—З–љ–Є —Б—В—А—Г–Ї—В—Г—А–Є, –Ї–Њ–Є—В–Њ –њ—А–µ–Ј 1970 –≥. —В–µ–Њ—А–µ—В–Є—З–љ–Њ –±—П—Е–∞ –Є–Ј—Б–ї–µ–і–≤–∞–љ–Є –Њ—В –∞–љ–≥–ї–Є–є—Б–Ї–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї –†–Њ–і–ґ—К—А –Я–µ–љ—А–Њ—Г–Ј, –∞ —Б–ї–µ–і —В–Њ–≤–∞ –µ–і–Є–љ –Є–Ј—А–∞–µ–ї—Б–Ї–Є —Д–Є–Ј–Є–Ї –Ф–∞–љ–Є–µ–ї –®–µ—Е—В–Љ–∞–љ (Daniel Shechtman) –≥–Є –Њ—В–Ї—А–Є, –Ј–∞ –Ї–Њ–µ—В–Њ –њ–Њ–ї—Г—З–Є –Э–Њ–±–µ–ї–Њ–≤–∞ –љ–∞–≥—А–∞–і–∞ –њ—А–µ–Ј 2011 –≥–Њ–і–Є–љ–∞. –Ґ–µ–Ј–Є –љ–µ–њ—А–∞–≤–Є–ї–љ–Є –Ї—А–Є—Б—В–∞–ї–Є —Б–µ –љ–∞—А–Є—З–∞—В –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є. –°—В—А—Г–Ї—В—Г—А–∞—В–∞ –Є–Љ –љ–µ —Б–µ –њ–Њ–≤—В–∞—А—П –њ–µ—А–Є–Њ–і–Є—З–љ–Њ –Є –≤—Б–µ –њ–∞–Ї –Ї—А–Є—Б—В–∞–ї–Є—В–µ —Б–∞ —Б—В–∞–±–Є–ї–љ–Є. (–≤–ґ "–Ъ–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ - –Љ–µ–ґ–і—Г –і–≤–∞ —Б–≤—П—В–∞").
–Р–≤—В–Њ—А–Є—В–µ –љ–∞ –Є–Ј—Б–ї–µ–і–≤–∞–љ–µ—В–Њ —Б–∞ —Б–µ –Њ–њ–Є—В–∞–ї–Є –і–∞ —А–∞–Ј–±–µ—А–∞—В –њ—А–Є—З–Є–љ–Є—В–µ.
–Ґ–µ –Є–Ј—Е–Њ–ґ–і–∞—В –Њ—В —В–Њ–≤–∞, —З–µ –≤ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–∞ –µ –Є—А–∞—Ж–Є–Њ–љ–∞–ї–љ–Њ—В–Њ —З–Є—Б–ї–Њ¬†–љ–∞ –Ј–ї–∞—В–љ–Њ—В–Њ —Б–µ—З–µ–љ–Є–µ 1.618. –Я—А–∞–≤–Є–ї–љ–Є—П—В –њ–µ—В–Њ—К–≥—К–ї–љ–Є–Ї —Б–µ –њ–Њ–і—З–Є–љ—П–≤–∞ –љ–∞ –Ј–ї–∞—В–љ–Њ—В–Њ —Б–µ—З–µ–љ–Є–µ –Є –≤—К–Ј –Њ—Б–љ–Њ–≤–∞ –љ–∞ –љ–µ–≥–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј–≥—А–∞–і–Є –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї —Б –Њ—Б–µ–≤–∞ —Б–Є–Љ–µ—В—А–Є—П —Б —К–≥–ї–Є –Њ—В 72 –≥—А–∞–і—Г—Б–∞.
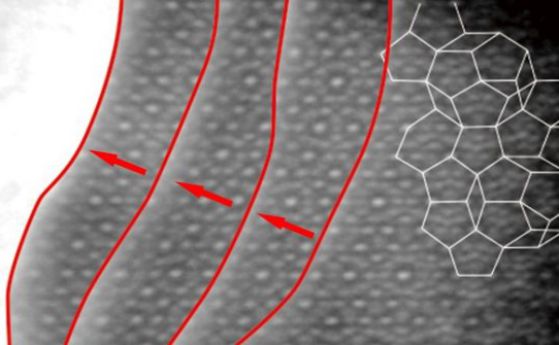
–Ш–Ј–њ–Њ–ї–Ј–≤–∞–є–Ї–Є —В–µ–Ј–Є –Є–Ј—З–Є—Б–ї–µ–љ–Є—П, —Г—З–µ–љ–Є—В–µ –њ–Њ—Б—В—А–Њ—П–≤–∞—В –Љ–Њ–і–µ–ї –љ–∞ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї. –Т –њ—А–Њ–µ–Ї—Ж–Є—П—В–∞ –љ–∞ –Љ–Њ–і–µ–ї–∞ –≤ —Ж–µ–љ—В—К—А–∞ —Б–µ –≤–Є–ґ–і–∞ —В–∞–Ј–Є —Б–Є–Љ–µ—В—А–Є—П –Њ—В 5-—В–Є –њ–Њ—А—П–і—К–Ї, –Ї–Њ—П—В–Њ –µ —Е–∞—А–∞–Ї—В–µ—А–љ–∞ –Ј–∞ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ –Є –Ј–∞–±—А–∞–љ–µ–љ–∞ –Ј–∞ –њ—А–∞–≤–Є–ї–љ–Є—В–µ –Ї—А–Є—Б—В–∞–ї–Є. –Ґ—П —Б–µ –њ—А–Њ—П–≤—П–≤–∞ –Ї–∞—В–Њ –і–µ—Б–µ—В —А–∞–і–Є–∞–ї–љ–Є –ї—К—З–Є, —В—А—К–≥–≤–∞—Й–Є –Њ—В —З–µ—А–≤–µ–љ–∞—В–∞ —В–Њ—З–Ї–∞. (–≤–ґ "–Э–µ–њ–µ—А–Є–Њ–і–Є—З–љ–Є—В–µ –Љ–Њ–Ј–∞–є–Ї–Є вАУ —Е–∞–Њ—Б –Є —А–µ–і –≤ –Ј–∞–±—А–∞–љ–µ–љ–Є —Б–Є–Љ–µ—В—А–Є–Є")

–Т –Љ–Њ–і–µ–ї–∞ –і–Њ–ї—Г –±–µ–ї–Є—В–µ —В–Њ–њ–Ї–Є —Б–∞ —З–∞—Б—В–Є—Ж–Є—В–µ, –∞ —З–µ—А–≤–µ–љ–Є—В–µ –Є –ґ—К–ї—В–Є —А—К–±–Њ–≤–µ - –µ–ї–µ–Ї—В—А–Њ–љ–љ–∞—В–∞ –≤—А—К–Ј–Ї–∞ –Љ–µ–ґ–і—Г —В—П—Е.

–£—Зe–љ–Є—В–µ –Є–Ј—Б–ї–µ–і–≤–∞—В –Њ–±—А–∞–Ј—Г–≤–∞–љ–µ—В–Њ –Є —Б—В–∞–±–Є–ї–љ–Њ—Б—В—В–∞ –љ–∞ –Є–Ї–Њ—Б–∞—Е–µ–і—А–∞–ї–љ–Є –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–љ–Є —Б—В—А—Г–Ї—В—Г—А–Є —Б –њ–Њ–Љ–Њ—Й—В–∞ –љ–∞ —Д–∞–Ј–Њ–≤–Њ—В–Њ –њ–Њ–ї–µ –љ–∞ –і–Є–љ–∞–Љ–Є—З–µ–љ –Ї—А–Є—Б—В–∞–ї–µ–љ –Љ–Њ–і–µ–ї. –Ґ–µ —Г—Б—В–∞–љ–Њ–≤–Є—Е–∞, —З–µ –љ–µ–ї–Є–љ–µ–є–љ–Є—В–µ –≤–Ј–∞–Є–Љ–Њ–і–µ–є—Б—В–≤–Є—П –Љ–µ–ґ–і—Г –≤—К–ї–љ–Є—В–µ –љ–∞ –њ–ї—К—В–љ–Њ—Б—В —Б¬†–і–≤–µ –і—К–ї–ґ–Є–љ–Є —Б—В–∞–±–Є–ї–Є–Ј–Є—А–∞ —В—А–Є–Є–Ј–Љ–µ—А–љ–Є—В–µ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є.
–Т –љ–Њ–≤–∞—В–∞ –њ—Г–±–ї–Є–Ї–∞—Ж–Є—П —Г—З–µ–љ–Є—В–µ –Њ–њ—А–µ–і–µ–ї–Є—Е–∞ —Б—Е–µ–Љ–∞—В–∞ –Є —Б—В–Њ–є–љ–Њ—Б—В–Є—В–µ –љ–∞ –њ–∞—А–∞–Љ–µ—В—А–Є—В–µ –љ–∞ —Д–∞–Ј–∞, –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Є –Ј–∞ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–∞ –і–∞ –і–Њ—Б—В–Є–≥–љ–µ –≥–ї–Њ–±–∞–ї–µ–љ –Љ–Є–љ–Є–Љ—Г–Љ –љ–∞ —Б—К—Б—В–Њ—П–љ–Є–µ—В–Њ –љ–∞ —Б–≤–Њ–±–Њ–і–љ–∞—В–∞ –µ–љ–µ—А–≥–Є—П. –Ґ–µ –њ–Њ–Ї–∞–Ј–∞—Е–∞, —З–µ –Є–Љ–∞ –і–≤–µ —З–µ—А—В–Є, –Ї–Њ–Є—В–Њ –і–Њ–њ—А–Є–љ–∞—Б—П—В –Ј–∞ –Њ–±—А–∞–Ј—Г–≤–∞–љ–µ—В–Њ –љ–∞¬†3D –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї.
–Я—К—А–≤–∞—В–∞ –µ, —З–µ –≤ —Б–Є—Б—В–µ–Љ–∞—В–∞ —Б–µ –њ—А–Њ—П–≤—П–≤–∞ —Б—К–Њ—В–љ–Њ—И–µ–љ–Є–µ—В–Њ –љ–∞¬†–Є—А–∞—Ж–Є–Њ–љ–∞–ї–љ–Њ—В–Њ —З–Є—Б–ї–Њ –љ–∞ –Ј–ї–∞—В–љ–Њ—В–Њ —Б–µ—З–µ–љ–Є–µ ѕЖ¬†–Љ–µ–ґ–і—Г¬†—З–∞—Б—В–Є—В–µ –љ–∞ –Љ–Њ–Ј–∞–є–Ї–∞—В–∞ –Ї–∞—В–Њ¬†–і—К–ї–ґ–Є–љ–Є –Є –Љ–∞—Й–∞–±–Є.
–Т—В–Њ—А–∞—В–∞ –µ, —З–µ —В–µ –Љ–Њ–≥–∞—В —Б–Є–ї–љ–Њ –і–∞ –њ–Њ–≤–ї–Є—П–≤–∞—В –µ–і–љ–∞ –љ–∞ –і—А—Г–≥–∞.
–Ґ–Њ–Ј–Є –Љ–Њ–і–µ–ї –њ–Њ–Ј–≤–Њ–ї—П–≤–∞ –і–∞ —Б–µ –Є–Ј—Б–ї–µ–і–≤–∞ —А–∞–Ј–ї–Є–Ї–∞—В–∞ –Љ–µ–ґ–і—Г —А–∞–Ј–ї–Є—З–љ–Є—В–µ –Љ–Њ–Ј–∞–є–Ї–Є –Є –і–∞ —Б–µ –Њ–њ—А–µ–і–µ–ї—П—В —Г—Б–ї–Њ–≤–Є—П—В–∞, –њ—А–Є –Ї–Њ–Є—В–Њ –µ–і–Є–љ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї –Љ–Њ–ґ–µ –і–∞ —Б–µ –Њ–±—А–∞–Ј—Г–≤–∞ –≤ –њ—А–Є—А–Њ–і–∞—В–∞.
"–Э–∞—И–µ—В–Њ –Є–Ј—Б–ї–µ–і–≤–∞–љ–µ –µ –љ–µ —Б–∞–Љ–Њ –Ї–Њ–љ—Ж–µ–њ—В—Г–∞–ї–љ–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞ –Є–і–µ—П, –≤ –љ–µ–≥–Њ –Є–Љ–∞ —Б—К—Й–Њ —В–∞–Ї–∞¬†–њ–µ—А—Б–њ–µ–Ї—В–Є–≤–∞ –Ј–∞ –Љ–љ–Њ–≥–Њ –њ—А–Є–ї–Њ–ґ–µ–љ–Є—П, –≤–Ї–ї—О—З–Є—В–µ–ї–љ–Њ —Б—К–Ј–і–∞–≤–∞–љ–µ—В–Њ –љ–∞ –≤–Є—Б–Њ–Ї–Њ–µ—Д–µ–Ї—В–Є–≤–µ–љ –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–µ–љ –ї–∞–Ј–µ—А", - –Ї–∞–Ј–≤–∞ –Я—А–Є—П –°—Г–±—А–∞–Љ–∞–љ–Є–∞–љ Priya (Priya¬†Subramanian), –Њ—В¬†–£–љ–Є–≤–µ—А—Б–Є—В–µ—В–∞ –≤ –Ы–Є–є–і—Б –Є –≤–Њ–і–µ—Й –∞–≤—В–Њ—А –љ–∞ —Б—В–∞—В–Є—П—В–∞.
–Ю—Й–µ –њ–Њ —В–µ–Љ–∞—В–∞

–Ъ–Њ—Б–Љ–Њ—Б
–Х—Б—В–µ—Б—В–≤–µ–љ–Є –Ї–≤–∞–Ј–Є—Б–Ї—А–Є—Б—В–∞–ї–Є —Б–µ –њ–Њ—П–≤—П–≤–∞—В –њ—А–Є —Б–±–ї—К—Б—К–Ї –≤ –∞—Б—В–µ—А–Њ–Є–і–љ–Є—П –њ–Њ—П—Б
–§–Є–Ј–Є–Ї–∞
–Ч–∞ –њ—К—А–≤–Є –њ—К—В –њ–Њ–Ї–∞–Ј–∞—Е–∞ –Ї–∞–Ї —А–∞—Б—В–∞—В –Ї–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ (–≤–Є–і–µ–Њ)

–Ь–∞—В–µ–Љ–∞—В–Є–Ї–∞
–Ъ–≤–∞–Ј–Є–Ї—А–Є—Б—В–∞–ї–Є—В–µ - –Љ–µ–ґ–і—Г –і–≤–∞ —Б–≤—П—В–∞


















–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
–Э—П–Љ–∞ –Ї–Њ–Љ–µ–љ—В–∞—А–Є –Ї—К–Љ —В–∞–Ј–Є –љ–Њ–≤–Є–љ–∞ !
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
–•—А–Є—Б—В–Є—П–љ–Є–љ
–Ґ–Њ–≤–∞ –µ –Ї—А–∞–ї—П—В –љ–∞ —В–Є–Ї–≤–Є—В–µ: –Ґ–Є–Ї–≤–∞—В–∞ –Љ—Г —В–µ–ґ–Є –љ–∞–і –µ–і–Є–љ –µ–і–Є–љ —В–Њ–љ