Досега разглеждахме само периодични мозайки, такива, които запълват равнината само с транслиране, без завъртане и огледално обръщане. Много плочки могат да съставят както периодични, така и непериодични мозайки.
 |
 |
 |
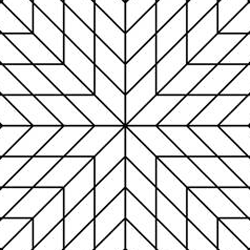
| Тези две мозайки са очевидно непериодични, получени са и с завъртане и с огледално обръщане и липсва елемент, който да запълни изцяло с транслиране равнината. | Същите плочки могат да съставят и периодична мозайка. Лесно може да се докаже че всеки триъгълник и четириъгълник може да го направи. | |
Съществуват безброй фигури, които могат да запълнят равнината непериодично, но същите могат да го направят и периодично. А дали има такива, които допускат само непериодично нареждане?
Дълго време се смяташе, че няма плочки и дори набори от няколко различни плочки, копия от които да могат да запълнят равнината само непериодично.
През 1964г. Робърт Бергър успява да построи такава мозайка от 20 426 различни плочки. По-късно той намерил множество от 104 плочки, а други математици ги намаляват до 24 и 6, докато със задачата не се заема оксфордския професор Роджър Пенроуз, чието основно занимания била квантовата механика, а с мозайки се е занимавал само за "забава".
Долу виждате първата негова непериодична мозайка с 4 вида плочки: петоъгълни, звезда, ромб и "хартиено корабче". Всяка комбинация от тези елементи ще съставя само непериодична мозайка.
 Илюстрация: American Mathematical Society |
Обърнете внимание на ротационната симетрия от 5-ти порядък - симетрия, която напълно липсваше при периодичните мозайки. |
Хвърчило и стрела
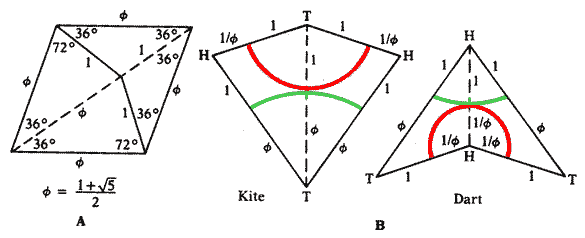
Той през 1974 г. Пенроуз намалява броя на фигурите до 2 - рекорд , неуспял да падне и до днес. Тези две прости фигури са проучени от Джон Хортън Конуей (същият, който е измислил играта "Живот", с която ви запознах преди време). Наречени са хвърчило и стрела (kite and dart). На схема А е показано как може да се получат от ромб, чиито по-дълъг диагонал е разделен в познатото ни златно сечение φ. Всяка страна е равна или на 1 или на φ.
 |
| Схема: Penrose Tilings and Quasicrystals |
Самият ромб се нарежда и периодично, но тази конфигурация е забранена. И за да се спазва по-лесно забраната, Конуей предлага да се нарисуват дъгите на схема B като при нареждането трябва да се съединяват само еднакви на цвят дъги.
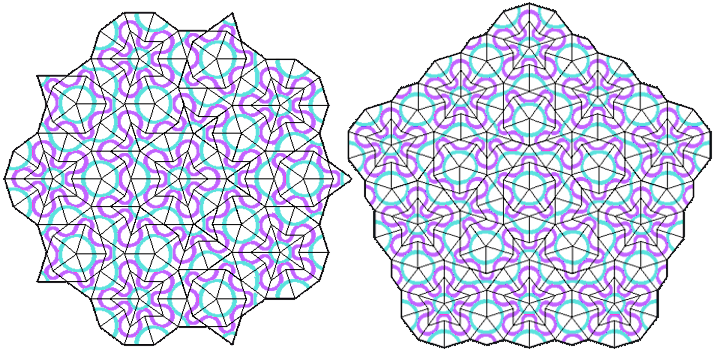 Илюстрация: University of Wisconsin (преработена от bgchaos) |
Левият модел е кръстен на звездата в центъра, се нарича Infinite Star Pattern, а десният съдържа десетоъгълник в центъра вместо на една звезда - наречен е Infinite Sun Pattern.
 Илюстрация: quadibloc.com |
Този вид облицовки нямат никаква транслационна симетрия, но те са самоподобни (понятие, известно ни от темата за фракталите) - едни и същи мотиви се появяват в различни мащаби и всяка конфигурация се повтаря безброй пъти.
Мозайка "двата ромба"
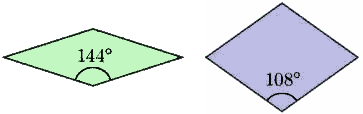
Третият вид, който предлага Пенроуз се състои от чифт ромбове с еднакви страни, но с различни ъгли.
|
Обикновените с форма на ромб плочки може да запълват равнината и периодично, така че е необходима забрана да бъдат съединявани: така, че да образуват успоредник, тъй като това ще позволи периодичност, но това ограничение не е достатъчно, за да осигури непериодичността , затова прибягваме какво при предишната мозайка до цветните дъги. |
 |
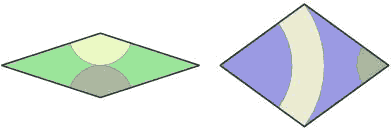 Илюстрация: American Mathematical Society |
По-долу е мозайка тип "двата ромба", съставена с помощните дъги. Те спомагат отново да изпъкне на места петоъгълната симетрия.
 Илюстрация: American Mathematical Society |
Може би забелязвате, че има малки петна от плочки, които изглежда да че се появят по няколко пъти, но ако огледате по-голяма част от мозайката ще се убедите, че няма очевидна транслационна симетрия. Също така, симетрията от пети порядък не е повсеместна. Има области, понякога доста големи, които нямат такава симетрия. |
|
Тази мозайка показва защо ограничението да не се образува успоредник не е достатъчно - вдясно е една несъмнено периодична облицовка. |
 Илюстрация: wikipedia |
Инфлация и дефлация
Хвърчилото и стрелата
|
Броят на различните подреждания на мозайките на Пенроуз е безкраен. За да се докаже това се разчита на едно необикновено свойство на тези мозайки, наречено от Конуей "инфлация" и "дефлация". За да се проследи това явление, трябва да се разреже стрелата по оста й на симетрия и да се "залепи " по показания начин.. |
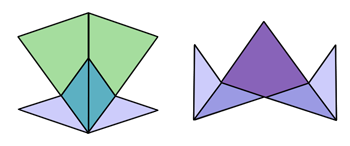 Илюстрация: bgchaos.com |
 Илюстрация: bgchaos.com, по идея на Penrose Tilings and Quasicrystals |
Като резултат ще се получи модел на друга мозайка с по-големи хвърчила и стрели, различаваща се от оригиналния модел. Инфлационният модел е подчертан с дебели линии. Тъй като новият модел е също мозайка с хвърчила и стрели, те също може да бъдат обединени в още по-големи хвърчила и стрели. Тази процедура може да се повтаря безкрайно. Това е безкрайна йерархия от мозайки, в която всяко "поколение" е по-голямо от своя предшественик. Подобен е и процеса на дефлация, създаването на мозайки на Пенроуз с по-дребни елементи, който също може да продължи до безкрайност. |
Двата ромба
Инфлацията при типа "двата ромба" се осъществява с малко по-сложно разделяне.
 Илюстрация: American Mathematical Society |
И картината на инфлация се вижда в долните илюстрации: вляво на "двата ромба", а вдясно - на първия тип мозайка на Пенроуз.
 Илюстрация: American Mathematical Society |
|
||||||||||||||||||
| Може изследвате сами инфлацията за мозайката от ромбове като преминете с мишката през 9-те етапа. | ||||||||||||||||||
| По елементи на American Mathematical Society | ||||||||||||||||||
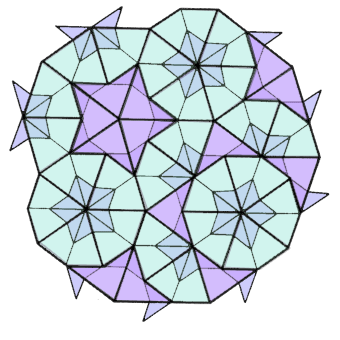
Ще забелязвате много повтарящи се мотиви, но ако ги проследите внимателно, ще се уверите че транслационна симетрия липсва. Има теорема, че ако един мотив има диаметър d, то на разстояние по-малко от 2d ще го срещнем отново.
Въобще непериодичните мозайки са една очарователна смес от ред и хаос, което заедно с "инфлационните" им качества им придава дълбоко философско значение. Те приличат на нещо като преходна форма от устойчивите и предсказуеми транслационни конструкции, носещи малък обем информация, към подвижност, към свободно движение, към информационно наситени структури, като своеобразно начало на преход от застиналите кристални форми към подвижните живи структури.
Символът на питагорейците и мозайките на Пенроуз
Има тясна връзка между двата типа мозайки на Пенроуз и златното сечение φ. Във "хвърчилото" и "стрелата" то присъства явно по дефиниция, а при двата ромба - чрез стойностите на ъглите. И двата типа обаче по удивителен начин се вписват в правилен петоъгълник.
Правилният петоъгълник (или пентагон ) и особено вписаната в него звезда (наричана и пентаграм, пентакъл) е древен знак от езически времена, натоварен с много смислови значения - почитан от вавилонци, питагорейци, бихайци, магьосници, военни, сатанисти и комунисти.
Но може би само математиците виждат причината за неговата привлекателност - вграденото в него златно сечение - отношението на страната на петоъгълника към диагона е 1: (1:1.61803398…). А страните на всеки последователно вписан петоъгълник е също в съотношение φ и така до безкрай. Плочките на мозайките на Пенроуз, вплетени в пентаграма, са в същата хармония
Източници:
Penrose Tiles Talk Across Miles, American Mathematical Society
Penrose Tilings and Quasicrystals, Eric Hwang
Penrose Tiles, Steven Dutch, Natural and Applied Sciences,
Penrose tiling, wikipedia
Tilings and Tesselations, Science U
An Introduction to Tilings, Cornell Mathematics
Penrose tiling, quadibloc.com
Занимателна математика, Мартин Гарднер
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари