Предлагаме ви със съкращения една статия на Николай К. Витанов и Златинка И. Димитрова от 82 брой на сп. "Българска Наука". В същия брой за първи път е публикувана статия на НаукаOFFNews "Солената вода на Марс".
Костите образуват скелета, който пък поддържа тялото. Костите подпомагат движението и защитават важни органи като мозъка, сърцето и белите дробове. Костите са леки (масата им е под 20 % от масата на човешкото тяло) и същевременно твърде устойчиви. Костите притежават известна еластичност, устойчиви са на натиск и опън. Костите образуват сложни костни системи, каквато е например гръбначният стълб.
С течение на времето, костите са започнали да се използват и за други дейности, след като някои животинки за развили зъби и челюсти. Та това със зъбите и челюстите продължава и при нас, хората. И оттук надолу ще ви разкажем някои интересни неща за биомеханиката на човешкото тяло.
А човешките тела могат да са доста различни. Което води до разлика в механичните им свойства. Но нека полека да видим какви са тези свойства на човешкото тяло.
Сили и въртящи моменти в биологичните системи.
Законите на Нютон си действат и в биомеханиката (затуй шансовете на дребния младеж да постигне нещо не са големи). Имаме сила на тежестта, която държи дебелия сумист (думата дебел в комбинация с думата сумист хич не е обида, а напротив – голям комплимент, защото никак не е лесно да се постигнат такива размери и килограми) здраво за земята, имаме и сила на триене, поради която дребничният младеж не може и да го помръдне назад. Може да се опита да усуче сумиста (тоест някакво въртеливо движение да направи) но и затова както казва народът, няма да му стигне силата. Е, значи трябва с хитрост. Тоест или подсичане на краката (да го спъне демек), но като гледаме, че съответния крак е по-дебел от подсичащия младеж, едва ли ще излезе нещо от тая работа. Може би опит за удар в контролния център – главата, би донесъл успех, но и това не става, защото нито ръката, нито кракът на младежа стигат да главата. Та така, след кратко разсъждение стигаме да извода, че младежът трябва да приложи прочутата хватка номер 13 – бягай! Ето как кратки разсъждения относно силата на тежестта ни доведоха до важно заключение.
И дойдохме на темата за силите в биомеханиката на човешкото тяло. Силата на тежестта е важна и това вече го разбрахме. Но не по-малко важни са и силите на мускулите. И какво толкова имате да ни разказвате за силите. Че ние знаем много неща за тях – ще кажете. Така е. Това, което искаме да ви представим, е гледната точка на биомеханиката за силите. Та от тази гледна точка, силите биват сили, свързани с натиск и сили, свързани с разпъване.
Още силите могат да действат от разстояние (като гравитацията или някои от силите, свързани с електромагнетизма) или пък да действат само при наличие на контакт между тела (каквато е силата на триене). Може би ще е интересно за по-младите ни читатели, че силите се представят чрез вектори и поради това сумирането им може да води до доста странни резултати (спомняте си приказката за орела, рака и щуката, които дърпали една талига, но резултатът от усилията им бил никакъв!)
Вероятно защото не са посещавали часовете по физика в съответното училище и то точно тогава, когато се е обяснявало как се сумират сили. Което повдига въпроса – как пък и тримата са пропуснали точно този час – но хайде да не се правим на Шерлок Холмс, че кой знае какво ще отрием тук).
Нека да отбележим, че голяма част от биомеханиката се занимава със задачи, свързани с макроскопични сили. А там действат железните „твърди” закони на Нютон (за разлика от не толкова „твърди” закони, действащи в науките за обществото например. Само да отбележим, че колкото по-„мек” е даден закон, толкова по-статистически характер има той. Тоест толкова повече той следва да се разглежда като тенденция, а не като твърдо правило). Някои специфични сили са силата на тежестта и мускулната сила. В човешкото тяло има около 600 мускула, които са отговорни за голяма част от движенията в него.
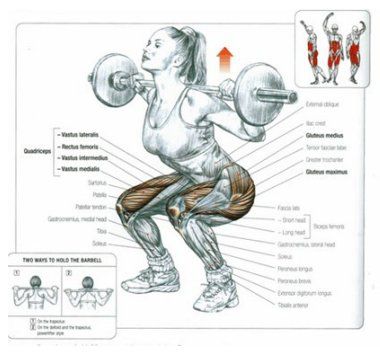Човекът е сложна биомеханична система. Управлявана от доста бърз биокомпютър. Всеки един от тези мускули може да се свива под действие на нервни импулси и се превръща в източник на сила. Искате пример ли – ами погледнете си ръката. Там имате едни мускули, наречени бицепс и трицепс. С тях сгъвате и разгъвате ръката. А в ръката може да има например гира от 5 килограма. И тъй мускулната сила движи гирата.
Друга важна сила е реакция на опората. Какво е това ли? Ами представете си, че решите да се пльоснете на някое (издържливо) диванче (щото ако не е издържливо пльосването може да свърши зле – за диванчето, де). Та пльосвате се вие и лежите на диванчето – тоест нещо ви пречи да продължите да падате към земята. Е, това, което компенсира гравитацията е реакцията на опората (в случая на диванчето). И ако гравитационната сила (пропорционална на масата ви) е по-малка от реакцията на опората, която маже да осигури бедното диванче, то диванчето се чупи, а вие продължавате победоносното си пльосване към пода, където усещането за реакция на опората може да е доста неприятно.
Някой скоро ще се пльосне. Но зад това пльосване има доста биомеханика на човешкото тяло. Както показва картинката вляво пльосването на земята може да става и по други начини. Картинката показва още, че в спорта има доста механика и върховите спортни постижения винаги се постигат и с помощта на изследвания в областта на биомеханиката.
Но да оставим това засега и да кажем няколко думи за силата на триене. Къде пък сега я виждаме тая сила – ще попитате. Ами отивате в парка да четете книжка (или пък да не четете книжка) и гледате как баба пуска внучката по пързалка. Сега си представете, че на пързалката няма сили на триене.
Ако пързалката е височка (като тая на , внучката доста ще се засили. Едно, че ще си ожули задните части, ами на края на пързалката и носа може да пострада (дечурлигата страшно го умеят падането по нос). Та тук силата на триене ни пази. Някои пързалки може и да са доста височки. И за намаляване на силата на триене се използва вода.
Сега да се съсредоточим върху въртенията, свързани с части на човешкото тяло и със свързаните с тези въртения въртящи моменти вследствие от действието на сили. Въртящите моменти са доста важни за всекидневния живот. Във физиката на въртящите моменти им казват още моменти на съответната сила. Въртящият момент също е вектор (тоест като се опитате да сумирате два въртящи момента резултатът може да не е това, което ви подсказва интуицията).
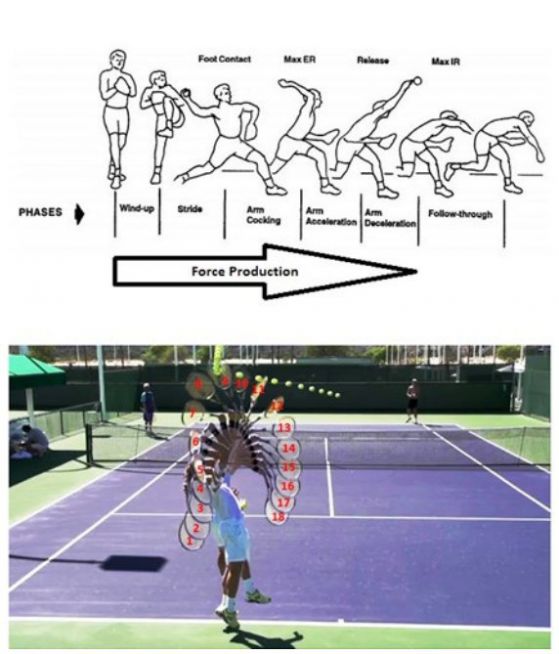
Доста въртеливи и други движения са необходими за да се хвърли една бейзболна топка. И при топките за тенис не е по-лесно.
Пример за въртящ момент ли искате да получите? Лесна работа – хващате си смартфончето (без да го вадите от калъфчето), слагате го на някаква равна повърхност и го завъртате с ръка. Вече може и сами да си представите как мозъкът ви праща съответните команди до мускулите на ръцете, как тези мускули се свиват и разпъват за да създадат мускулните сили, които движат ръката. И както се казва по рекламите – но това не е всичко. Ръката трябва да предаде силата на смартфончето. И понеже още не сте усвоили уменията на Дарт Вейдър, това предаване става чрез силите на триене между ръката и калъфчета. Ако тези сили са подходящо насочени, калъфчето (и смартфончето) ще почне да се върти. Ако силите не са подходящо насочени, можете да си контактувате колкото си искате с калъфчето и никакво въртене няма да се получи. А пък полезните въртеливи движения на части от ръцете са най – различни – виж например:
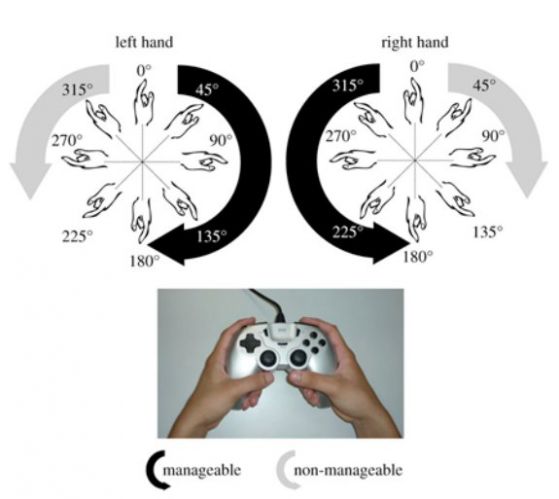
Вероятно и без допълнителни приказки тази фигура убеждава по-младите ни читатели, че изучаването на въртеливите движения на ръцете е много важно.
Ама дайте и пример за въртящ момент на сила и от човешкото тяло де – ще каже някой. Лесна работа. Взимате едно камъче – към половин – едно кило. Изпъвате ръката напред (добре, че не ви накарахме да вземете камъче от 20 кила, нали). Отпускате ръката надолу без да я свивате и после пак я вдигате. Като правите това, усещате, че много мускули доста се понапрягат. За какво е тоз мускулен зор. Ами за да подпомогнат вашите мераци да си движите ръката, като създават въртящ момент с ос на въртене покрай раменната ви става. Та така – една от нашите цели е полека да ви убедим, що за чудна машинка е човешкото тяло.
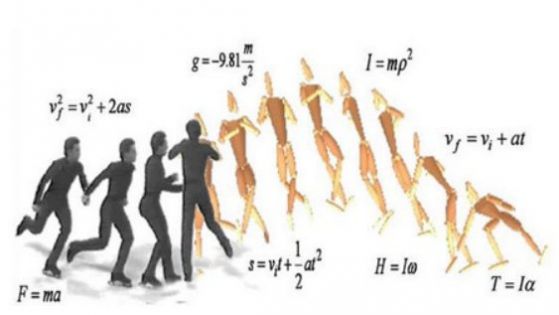
Завъртането с подскок при фигурното пързаляне също не е проста задача.
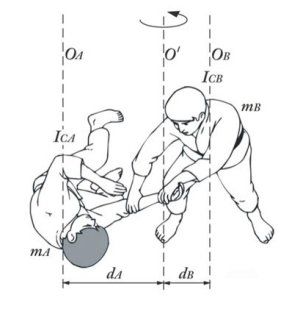
А ако искате да си помислите още по въпроса за въртящите моменти, представете си танцова двойка от фигурното пързаляне и разгледайте случаи на различни съотношения между масите на двамата партньори – някои насоки на разсъждение може да получите от фигурата горе. Или пък, отново идете на детската площадка и се позамислете как ли функционират люлките или люлеещите се пейки. И да не забравите, че въртящият момент зависи от разстоянието до оста на въртене и от големината на силата. Та не се чудете, когато от едната страна на пейката е детенцето и е седнало към края и, а от другата страна е таткото, седнал по-към средата (за да намали разстоянието си до оста на въртене) и си помага с краката, за да се движи пейката (това сами си го обяснете защо е така).
Център на тежестта
И тъй, нека караме по-натам. Повечето от нас могат да стоят прави. Ама защо? Защо не се сгромолясваме на земята? То е ясно вече, че има реакция на опората и ако тя е малка (като в блатата) може да почнем и да потъваме. Но да речем, че реакцията на опората е достатъчна. Тогава пък може да ни се появи въртящ момент и да се къпичнем. Ама и това не става. Защо? Ами защото мозъкът ни държи този въртящ момент малък, като позиционира центъра на тежестта ни да е много близо до равнината на симетрия на човешкото тяло. Така векторното произведение от силата на тежестта и рамото на силата (от центъра на тежестта до земята) е почти нула и ние както се казва, пазим равновесие.
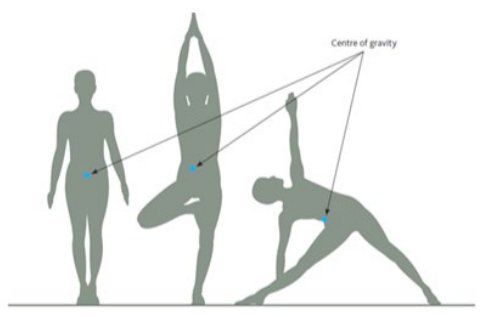
Центърът на тежестта и неговото отместване при различни позиции на човешкото тяло.
Центърът на тежестта е точката, в която може да считаме, че е приложена силата на тежестта, съответна на разглежданото тяло (в нашия случай – на разглежданото човешко тяло). Защо може да считаме, че сумата от силите на тежестта съответни на всички клетки в човешкото тяло може да се приложи в една точка е доста интересен въпрос и физиците учат една теорема по този въпрос. Но нека да приемем, че това е така и да не разсъждаваме повече по въпроса (е, на който му е интересно може да порови и да намери съответната теорема). Добре е човек да знае къде е центърът на тежестта му. Това ще му позволи например да ходи по въже, да застане на главата си без да падне или пък… да стане от стола. Мислите си, че това със стола е майтап, нали? Добре – седнете изправени на един стол и изпънете краката си напред (нека да опират земята). Хайде сега опитайте да станете без да си помагате с ръце и без да свивате краката и без да накланяте тялото напред. Ще станете, ама друг път. И защо няма да станете? Защото центърът на тежестта ви е много назад, а не между стъпалата на краката. Та така, като повторите и потретите този опит, ще се убедите колко е важен центърът на тежестта.
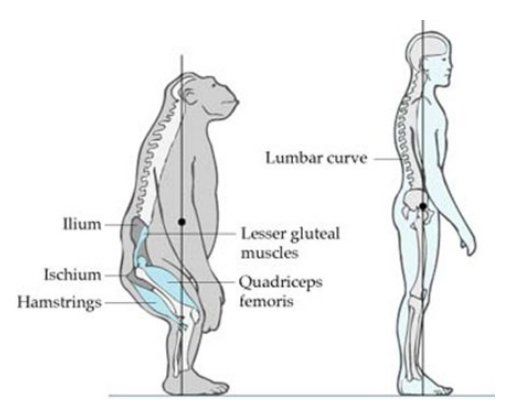
Центърът на тежестта – някога и сега.
Ако човек е изправен, то центърът на тежестта му се намира по средата на стъпалата му и в средата на двете стъпала. Ако такъв човек се повдигне на пръсти, то центърът на тежестта му отива на нивото на основата на палците на краката и пак е по средата между двете стъпала. Но забележете – когато човек се е изправил на пръсти, контактната площ на стъпалата му със земята е доста по-малка, отколкото когато е стъпил здраво на земята. Поради това, човек, който се е повдигнал на пръсти е по-лесно да бъде изваден от равновесие (центърът на тежестта по-лесно може да бъде изваден извън площта на контакт на стъпалата със земята).
Ротации (завъртания)
Завъртанията на човешкото тяло са доста интересни, тъй като те зависят не само от масата на тялото, но и от разпределението на тази маса относно оста на въртене. Например, представете си, че вие сте кавалер и танцувате с дама и трябва да я завъртите около вертикалната и ос. Това не е трудна работа. Доста по трудно е, когато дамата трябва да бъде в хоризонтална позиция и вие да я завъртите около собствената си ос. Все едно и също дамско тяло – но при втория начин на завъртане може доста да се озорите.
Защо това е така, можете да си отговорите с помощта на една величина, наречена инертен момент. Инертният момент в света на въртенето е като масата в света на постъпателното движение – колкото е по-голям инертният момент, толкова е по-трудно въртенето (сега май започва да ви се прояснява защо гимнастиците се опитват да се свият на кълбо, като трябва да правят превъртания – така те намаляват инертния момент на тялото си и се въртят по-лесно). Въртящият момент на едно тяло е равен на инертния му момент по ъгловото му ускорение. В света на въртенето въртящият момент играе ролята на силата от света на движението на материалната точка. Та когато въртящият момент е фиксиран, то трябва да намалим инертния момент на тялото (да се свием) за да има по-голямо ъглово ускорение (тоест да направим превъртането без да паднем по нос).
За инертният момент на човешкото тяло и промяната му при свиване.
Та значи, важно е да можем да пресметнем инертния момент на човешкото тяло и на неговите части. Няма да даваме точните стойности, но инертният момент на човек свит на кълбо е около 2 пъти и половина по-малък от инертния момент на изправен човек. Затова гимнастиците гледат да се свият, когато се превъртат. Някой ще вземе да попита – а какво за случая на въртене е еквивалентно на енергията за случая на движение на материална точка. Еквивалентното нещо се нарича ъглов момент и той е равен на …, да правилно на инертния момент (аналог на масата) умножен по ъгловата скорост (аналог на скоростта). Хайде пак обратно на нашия гимнастик. Засилил се значи и тръгва да се превърта. Запазил демек някакъв ъглов момент. Иска да се върти с по-голяма ъглова скорост ли? Сеща се за закона за запазване на ъгловия момент – като искаш да се въртиш с по-голяма ъглова скорост, трябва да намалиш инертния момент. Ами, свий се де! Инертния ти момент намалява два пъти и половина и се въртиш по-бързо. Или пък да разгледаме какво правят балерините. Свие ръцете – инертният момент намалява и се върти по-бързо около оста си. Разпери ръцете и въртенето се забавя. И вероятно никога не е чувала за закона за запазване на ъгловия момент.
Забиването при волейбола.
И сега – малко по-хитър пример. Вглеждали ли сте се във волейболистка, който забива топката. Ръката, която забива, извършва въртеливо движение. Тоест имаме ъглов момент. Но сумарният ъглов момент трябва да е нула – нямало е ъглов момент преди началото на забиването. И къде е компенсиращия ъглов момент, а? Ами вгледайте се в краката на волейболистката, де. Единия крак извършва въртеливо движение около ос, свързана с коляното и то в посока, противоположна на движението на ръката. И тъй сумарният ъглов момент остава нула.
Мускулна сила и прости машини
Много от работата, вършена от мускулите на човешкото тяло, почива на принципа на лоста. Работата по преместване на точкова маса във физиката е равна на силата по изминатия от масата път. Ако намерим начин да удължим пътя по който прилагаме силата, то намаляваме силата и така можем да преместваме големи тежести. Един начин да правим фокуса с дългия път и малката сила, е да използваме лост. Има лостове от първи род, лостове от втори род (и лостове от трети род!!).
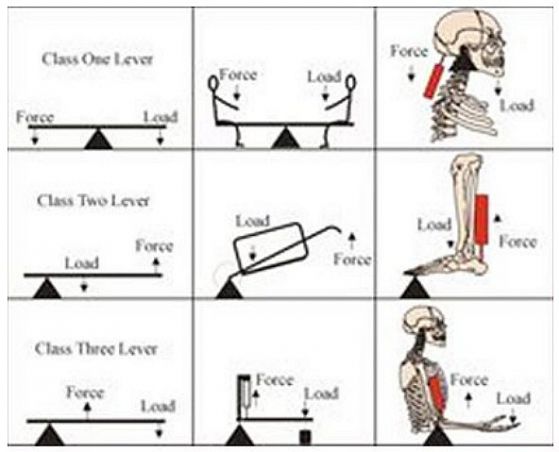
Лостове от първи, втори и трети род.
Важна характеристика на един лост е механичното предимство: това е отношението на силата (обикновено силата на тежестта на някое тяло) която трябва да преодолеем към силата, която трябва да приложим към лоста, за да свършим работата. Добре, стига за теорията на лостовете – ще кажете. И ще попитате – а къде има лостове из човешкото тяло? Ами погледнете си ръката – от дланта до лакътя. Тя си е жив лост, който се движи от мускула, наречен бицепс. И този лост ни служи доста добре – движим с него храна към устата например. И този лост е от…. трети род! – опорната точка е в лакътя, бицепсът е закачен след тази опорна точка по посока на дланта, а тежестта, която се мести, обикновено е в ръката. Лост от първи род движи главата. Опорната точка е в гръбначния стълб – малко зад ухото, тежестта на главата е пред ухото, а силата, която прилагаме, идва от мускулите на врата, които са от другата страна на ухото. Лост от втори род е стъпалото ни. Там опорната точка е малко след пръстите, силата на тежестта е съвсем малко по-натам по посока на петата, а мускулите на прасеца са съвсем до петата. И тъй нататък и тъй нататък – ако се замислите, ще откриете още доста лостове из човешкото тяло.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
6005
1
04.02 2018 в 20:48
Поздрави! :)
Последни коментари