Когато се направи ново откритие във физиката, вероятно сте чували да се използва терминът „сигма“. Какво означава това? Защо е толкова важно да се говори за сигма, когато се прави претенция за ново откритие? И защо особено пет сигма е толкова важна?
Защо физиката на елементарните частици разчита на статистика?
Частиците, произведени при сблъсъци в Големия адронен колайдер (LHC), са малки и изключително краткотрайни. Тъй като те почти веднага се разпадат на други частици, за физиците е невъзможно директно да ги „видят“. Вместо това те разглеждат свойствата на крайните частици, като техния заряд, маса, спин и скорост. Те работят като детективи: крайните продукти предоставят улики за възможните трансформации, на които са претърпели частиците, докато са се разлагали. Вероятностите за тези така наречени „канали на разпадане“ се предвиждат от теорията.
В LHC милиони сблъсъци на частици в секунда се проследяват от детекторите и се филтрират през системи за задействане, за да се идентифицират разпадането на редки частици. След това учените анализират филтрираните данни, за да търсят аномалии, които могат да показват нова физика.
Както при всеки експеримент, винаги има шанс за грешка. Фоновият шум може да причини естествени колебания в данните, водещи до статистическа грешка. Има също потенциал за грешка, ако няма достатъчно данни, или системна грешка, причинена от дефектно оборудване или малки грешки в изчисленията. Учените търсят начини да намалят въздействието на тези грешки, за да гарантират, че твърденията, които правят, са възможно най-точни.
Какво е статистическа значимост?
Представете си, че хвърляте обикновен зар. Има вероятност едно към шест да получите едно число. Сега си представете, че хвърляте два зара – вероятността да получите определено общо число варира – има само един начин да хвърлите две и шест различни начина да хвърлите седем. Ако хвърлите два зара много, много пъти и запишете резултатите си, формата на графиката ще следва камбановидна крива, известна като нормално разпределение.
Нормалното разпределение има някои интересни свойства. То е симетрично, пикът му се нарича средна стойност, а разпространението на данните се измерва с помощта на стандартно отклонение. За данни, които следват нормално разпределение, вероятността точка от данни да е в рамките на едно стандартно отклонение от средната стойност е 68%, в рамките на две е 95%, в рамките на три е още по-висока.
Стандартното отклонение е представено от гръцката буква σ или сигма. Измерена чрез брой стандартни отклонения от средната стойност, статистическата значимост е колко далеч се намира определена точка от данни от очакваната стойност.
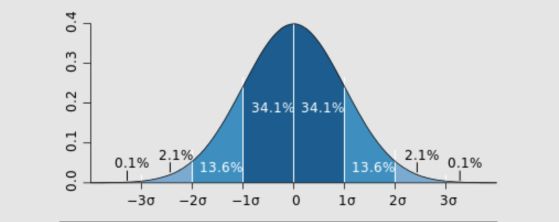Графика, показваща камбановата крива на нормално разпределение със зони, показващи стандартните отклонения
За данни, които следват нормално разпределение, вероятността точка от данни да е в рамките на едно стандартно отклонение или една сигма (σ) от средната стойност е 68%, в рамките на две σ е 95%, в рамките на три σ е дори по-висока. Кредит: MW Toews
Какво общо има това с физиката?
Когато учените записват данни от LHC, естествено е да има малки статистически колебания, но те обикновено са близки до очакваната стойност. Има индикация за нов резултат, когато има по-голяма аномалия. В кой момент тази аномалия може да се класифицира като нов феномен? Учените използват статистика, за да установят това.
Представете си отново метафората със зара. Освен този път, вие хвърляте един зар, но не знаете дали е фалшив. Хвърляте го веднъж и получавате три. Няма нищо особено значимо в това – имаше шанс едно към шест за вашия резултат – имате нужда от повече данни, за да определите дали е подправен. Хвърляте го два пъти, три пъти, още повече и всеки път попадате на тройка. В кой момент можете да потвърдите, че зарът е подправен?
Няма конкретно правило за това, но след около осем пъти получаване на едно и също число, може да бъдете доста сигурни, че това е така. Шансът това да се случи случайно е само (1/6)8 = 0,00006%.
По същия начин физиците определят дали дадена аномалия наистина е резултат. С все повече и повече данни вероятността от статистическа флуктуация в една и съща определена точка става все по-малка и по-малка. В случая с Хигс бозона на физиците са били нужни достатъчно данни, за да може статистическата значимост да премине прага от пет сигма. Едва тогава те биха могли да обявят откриването на „подобна на Хигс частица“.
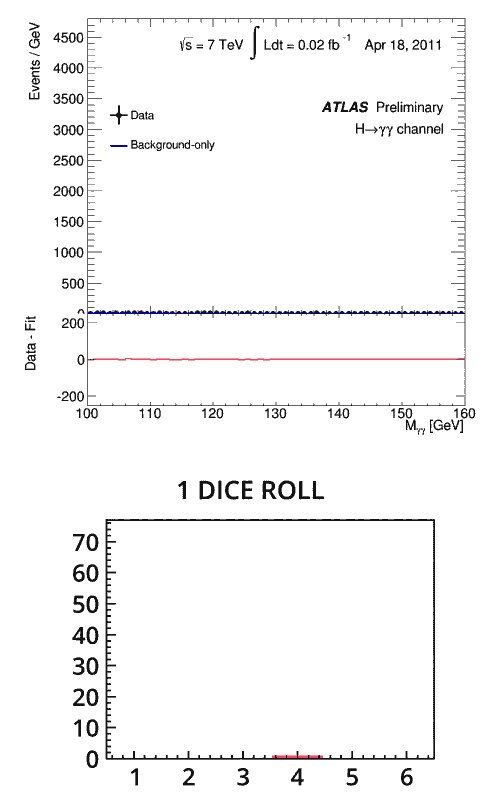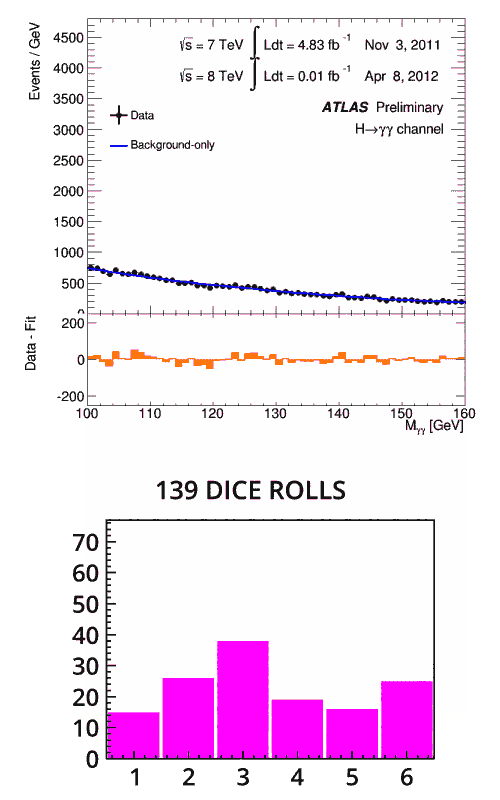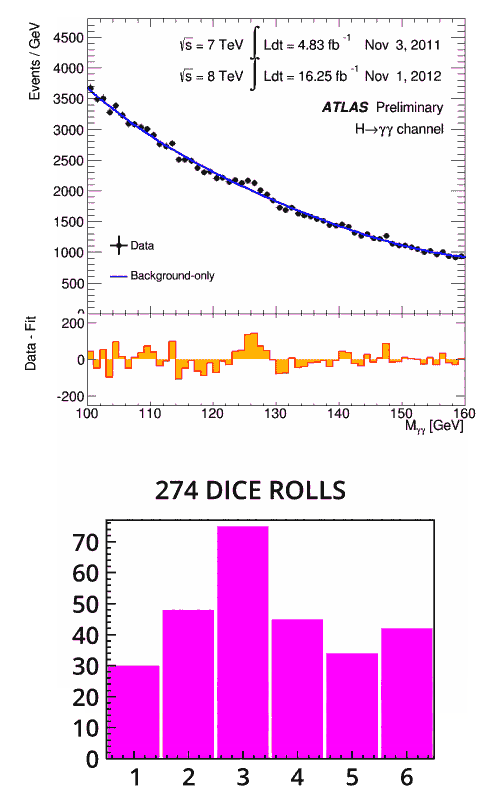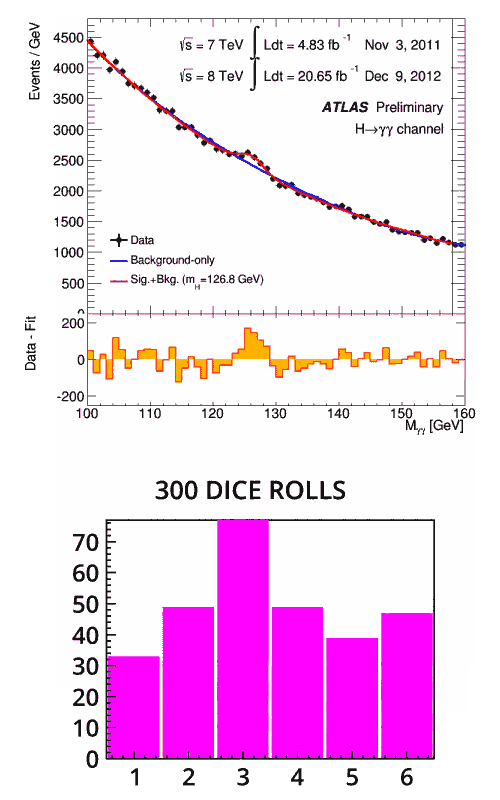
Първо изображение: Анимация на реконструирана маса от кандидат-събития на Хигс при двуфотонни разпадания. Изпъкналостта на графиката съответства на масата на Хигс бозона. Кредит: ATLAS/CERN
Второ изображение: Анимация на резултатите от 300 хвърляния на зарове, където зарът е бил манипулиран, за да показва числото 3 по-често от очакваното. Кредит: Piotr Traczyk/CERN
Какво означава, когато физиците казват, че данните имат статистическа значимост от пет сигма?
Резултат, който има статистическа значимост от пет сигма, означава почти сигурната вероятност пикът в данните да е причинен от ново явление, а не от статистическа флуктуация. Учените изчисляват това чрез измерване на сигнала спрямо очакваните флуктуации на фоновия шум в целия диапазон.
За някои резултати, чиито аномалии могат да лежат във всяка посока над или под очакваната стойност, значимостта на пет сигма е 0,00006% вероятност данните да са шум.
За други резултати, като откритието на бозона на Хигс, значимостта на пет сигма е 0,00003% вероятност за статистическа флуктуация, тъй като учените търсят данни, които надвишават стойността на пет сигма на половината от графиката на нормалното разпределение.
Защо пет сигма е особено важна за физиката на елементарните частици?
В повечето области на науката, които използват статистически анализ, прагът от 5 сигма изглежда пресилен. При изследване на населението, като например анкети за това как хората ще гласуват, обикновено е достатъчен резултат със статистическа значимост 3 сигма. Но когато обсъждат самата структура на Вселената, учените се стремят да бъдат възможно най-точни. Резултатите от фундаменталната природа на материята са силно въздействащи и имат значителни последици, ако са грешни.
В миналото физиците са отчитали резултати, които биха могли да свидетелстват за нови открития, макар данните да са имали статистическа значимост само от 3 до 4 сигма. Често те са били опровергавани при събирането на повече данни.
Ако е налице систематична грешка, например неправилно изчисление, високата първоначална значимост от пет сигма може да означава, че резултатите не са напълно недействителни. Това обаче означава, че резултатът не е окончателен и не може да се използва за твърдение за ново откритие.
Пет сигма се смятат за "златен стандарт" във физиката на елементарните частици, тъй като гарантират изключително малка вероятност дадено твърдение да е невярно.
Но не всички пет сигми са еднакви...
Пет сигма е общоприетата стойност за статистическа значимост при откриването на нови частици в рамките на Стандартния модел - тези частици, които са предсказани от теорията и се намират в рамките на сегашното ни разбиране за природата. Значимостта от пет сигми се приема и при търсене на специфични свойства на поведението на частиците, тъй като вероятността да се открият колебания в други части на диапазона е по-малка.
Дали пет сигма е достатъчна статистическа значимост, може да се определи, като се сравни възможността за нова хипотеза с вероятността тя да е статистическа флуктуация, като се вземе предвид теорията.
За физика извън Стандартния модел или за данни, които противоречат на общоприетата физика, се изисква много по-висока стойност на статистическата значимост - на практика достатъчна, за да се "опровергае" предишната физика. В статията си "Значението на пет сигма" физикът Луис Лайънс (Louis Lyons) предлага резултатите за по-невероятни явления да имат по-висока статистическа значимост, например 7 сигма за откриването на гравитационни вълни или откриването на пентакварки.
В тази статия Лайънс също така смята, че статистическата значимост от пет сигма е достатъчна за откриването на Хигс бозона. Това е така, защото теорията за Хигс бозона е предсказана, математически тествана и общоприета от общността на физиците на елементарните частици много преди LHC да създаде условия за неговото наблюдение. Но след като това беше постигнато, все още се налага да се установи висока статистическа значимост, за да се определи дали откритият сигнал наистина е откритие.
Статистическа значимост от пет сигма е строга, но тя наистина е минимална. По-високата стойност на статистическата значимост затвърждава данните като по-надеждни. Постигането на резултати със статистическа значимост от 6, 7 или дори 8 сигма обаче изисква много повече данни, много повече време и много повече енергия. С други думи, вероятност от най-много 0,00006%, че новото явление не е статистическа случайност, е достатъчно добра.
Справка: “The significance of five sigma”; Louis Lyons; https://arxiv.org/pdf/1310.1284.pdf
Източник: Why do physicists mention “five sigma” in their results?, CERN
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари