

–Т—К–≤–µ–і–µ–љ–Є–µ –≤ –њ–Њ–љ—П—В–Є–µ—В–Њ "–Є—В–µ—А–∞—Ж–Є—П"
–Ш–Ј–Њ–±—А–∞–Ј—П–≤–∞–љ–µ—В–Њ –љ–∞ —Д—А–∞–Ї—В–∞–ї–Є –µ —В—П—Б–љ–Њ —Б–≤—К—А–Ј–∞–љ–Њ —Б –њ—А–Њ–≥—А–∞–Љ–Є—А–∞–љ–µ—В–Њ. –Ч–∞ —Е–Њ—А–∞, –Ї–Њ–Є—В–Њ –Є–Љ–∞—В –і–Њ—А–Є –±–µ–≥–ї–∞ –њ—А–µ–і—Б—В–∞–≤–∞ –Њ—В –њ—А–Њ–≥—А–∞–Љ–Є—А–∞–љ–µ, —В–µ–Ј–Є –њ–Њ–љ—П—В–Є—П¬†—Б–∞¬†—П—Б–љ–Є. –Ч–∞ –і—А—Г–≥–Є—В–µ:
–Ш—В–µ—А–∞—Ж–Є—П –≤ –њ—А–Њ–≥—А–∞–Љ–Є—А–∞–љ–µ—В–Њ –µ —В–∞–Ї–∞–≤–∞¬†–Њ—А–≥–∞–љ–Є–Ј–∞—Ж–Є—П –љ–∞ –Њ–±—А–∞–±–Њ—В–Ї–∞—В–∞ –љ–∞ –і–∞–љ–љ–Є, –њ—А–Є –Ї–Њ—П—В–Њ –і–µ–є—Б—В–≤–Є–µ—В–Њ —Б–µ –њ–Њ–≤—В–∞—А—П –љ—П–Ї–Њ–ї–Ї–Њ –њ—К—В–Є, –±–µ–Ј —В–Њ–≤–∞ –і–∞ –і–Њ–≤–µ–і–µ –і–Њ –њ–Њ–ї–Њ–ґ–µ–љ–Є–µ, –њ—А–Є –Ї–Њ–µ—В–Њ —Д—Г–љ–Ї—Ж–Є—П—В–∞ –і–∞¬†–Є–Ј–≤–Є–Ї–∞ —Б–∞–Љ–∞ —Б–µ–±–µ —Б–Є (—В–Њ–≤–∞ –≤–µ—З–µ –µ —А–µ–Ї—Г—А—Б–Є—П).
–Ъ–Њ–≥–∞—В–Њ –љ—П–Ї–Њ–Є –і–µ–є—Б—В–≤–Є—П —В—А—П–±–≤–∞ –і–∞ —Б–µ –њ–Њ–≤—В–Њ—А—П—В –љ—П–Ї–Њ–ї–Ї–Њ –њ—К—В–Є, —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В¬†—Ж–Є–Ї—К–ї. –Э–∞–є-–ї–µ—Б–љ–Њ —Й–µ –≤–Є —Б—В–∞–љ–µ —Б –љ—П–Ї–Њ–є –њ—А–Є–Љ–µ—А
|
n=1; for i=0 to i<5 step=1  {n=n+i;} |
–Ґ–Њ–Ј–Є –њ—А–Њ—Б—В —Д—А–∞–≥–Љ–µ–љ—В –Њ—В –љ–µ–Њ–њ—А–µ–і–µ–ї–µ–љ –µ–Ј–Є–Ї –Ј–∞ –њ—А–Њ–≥—А–∞–Љ–Є—А–∞–љ–µ (–њ—А–Є–љ—Ж–Є–њ—К—В –µ –µ–і–Є–љ –Є —Б—К—Й, —Б–∞–Љ–Њ —Б–Є–љ—В–∞–Ї—Б–Є—Б—К—В –µ —А–∞–Ј–ї–Є—З–µ–љ) –Љ–Њ–ґ–µ –і–∞ —Б–µ —В—К–ї–Ї—Г–≤–∞ —В–∞–Ї–∞:¬† n –њ—А–Є–µ–Љ–∞ –љ–∞—З–∞–ї–љ–∞ —Б—В–Њ–є–љ–Њ—Б—В 1. –Я–Њ—Б–ї–µ –≤–ї–Є–Ј–∞ –≤ —Ж–Є–Ї—К–ї, –Ї–Њ–є—В–Њ —Б–µ –Њ–њ—А–µ–і–µ–ї—П –Њ—В –њ–∞—А–∞–Љ–µ—В—К—А–∞ i —Б –љ–∞—З–∞–ї–љ–∞ —Б—В–Њ–є–љ–Њ—Б—В 0 , –Ї–∞—В–Њ —Б–ї–µ–і –≤—Б—П–Ї–∞ —Б—В—К–њ–Ї–∞ —Г–≤–µ–ї–Є—З–∞–≤–∞ —Б—В–Њ–є–љ–Њ—Б—В—В–∞ —Б–Є —Б 1, –і–Њ–Ї–∞—В–Њ i –Њ—Б—В–∞–≤–∞ –њ–Њ-–Љ–∞–ї–Ї–Њ –Њ—В 5, –≤ —Б–ї—Г—З–∞—П. –Ф–µ–є—Б—В–≤–Є–µ—В–Њ –≤ —В—П–ї–Њ—В–Њ –љ–∞ —Ж–Є–Ї—К–ї–∞ –≤—К—А—Е—Г –Њ–њ–µ—А–∞—Ж–Є—П—В–∞¬†n=n+i,¬†–Ј–∞ –≤—Б—П–Ї–∞ –µ–і–љ–∞ —Б—В—К–њ–Ї–∞ –Њ—В —Ж–Є–Ї—К–ї–∞ —Б–µ –љ–∞—А–Є—З–∞ –≤—Б—К—Й–љ–Њ—Б—В –Є—В–µ—А–∞—Ж–Є—П. –Ґ—А—П–±–≤–∞ –і–∞ —Б–µ –Њ—В–±–µ–ї–µ–ґ–Є, —З–µ –Є–Ј—А–∞–Ј–Є—В–µ –≤ –њ—А–Њ–≥—А–∞–Љ–Є—А–∞–љ–µ—В–Њ —Б–µ –Є–Ј–≤—К—А—И–≤–∞—В –Њ—В –і—П—Б–љ–Њ –љ–∞–ї—П–≤–Њ. |
|
–†–µ–Ј—Г–ї—В–∞—В—К—В –Њ—В —В–Њ–Ј–Є –њ—А–Њ—Б—В –њ—А–Є–Љ–µ—А –Ј–∞ n —Й–µ –µ:¬†n=1; n=2;¬†n=3;¬†n=4; |
–Э–∞–є-–Њ–±—Й–Њ, –Є—В–µ—А–∞—Ж–Є—П –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–≤–µ–і–µ –Ї–∞—В–Њ "–њ–Њ–≤—В–Њ—А–µ–љ–Є–µ".
–Т—К–≤ –≤—Б–µ–Ї–Є —Д—А–∞–Ї—В–∞–ї –Є–Љ–∞ –±–µ–Ј–Ї—А–∞–є–љ–Њ –њ–Њ–≤—В–∞—А—П—Й–∞¬†—Б–µ —Д–Њ—А–Љ–∞. –Я—А–Є —Б—К–Ј–і–∞–≤–∞–љ–µ —В–∞–Ї—К–≤ —Д—А–∞–Ї—В–∞–ї, –љ–∞–є-–њ—А–Њ—Б—В–Є—П—В –љ–∞—З–Є–љ —Б–µ —Б—К—Б—В–Њ–Є –≤ —В–Њ–≤–∞, –і–∞ —Б–µ –њ–Њ–≤—В–Њ—А—П—В –љ—П–Ї–Њ–ї–Ї–Њ –і–µ–є—Б—В–≤–Є—П, –Ї–Њ–Є—В–Њ —Б—К–Ј–і–∞–≤–∞—В —В–∞–Ј–Є —Д–Њ—А–Љ–∞. –Т–Љ–µ—Б—В–Њ –і—Г–Љ–∞—В–∞ "–њ–Њ–≤—В–Њ—А–µ–љ–Є–µ" –Є–Ј–њ–Њ–ї–Ј–≤–∞–Љ–µ "–Є—В–µ—А–∞—Ж–Є—П". –§–∞–Ї—В–Є—З–µ—Б–Ї–Є –≤—Б–µ–Ї–Є —Д—А–∞–Ї—В–∞–ї –Љ–Њ–ґ–µ –і–∞ –±—К–і–µ —Б—К–Ј–і–∞–і–µ–љ —Б –Є—В–µ—А–∞—Ж–Є–Є –љ–∞ –љ—П–Ї–∞–Ї–≤–Њ –њ—А–∞–≤–Є–ї–Њ. –Ч–∞ –і–∞ —Б–µ —Б—К–Ј–і–∞–і–µ –Є—Б—В–Є–љ—Б–Ї–Є —Д—А–∞–Ї—В–∞–ї, —В—А—П–±–≤–∞ –і–∞ —Б–µ –Є–Ј–≤—К—А—И–Є –Є—В–µ—А–∞—Ж–Є—П—В–∞ –±–µ–Ј–Ї—А–∞–є–љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—К—В–Є. –Э–Њ –±–Є—Е–Љ–µ –Љ–Њ–≥–ї–Є –і–∞ —П –Є–Ј–њ—К–ї–љ–Є–Љ –Ї—А–∞–µ–љ –±—А–Њ–є –њ—К—В–Є, –љ–Њ –і–Њ—Б—В–∞—В—К—З–љ–Њ –Љ–љ–Њ–≥–Њ, –Ј–∞ –і–∞ —Б–Є —Б—К–Ј–і–∞–і–µ–Љ –њ—А–µ–і—Б—В–∞–≤–∞ –Ј–∞ "–Є—Б—В–Є–љ—Б–Ї–Є—П" —Д—А–∞–Ї—В–∞–ї. –Х—Б—В–µ—Б—В–≤–µ–љ–Њ —Б –њ–Њ–Љ–Њ—Й—В–∞ –љ–∞ –Ї–Њ–Љ–њ—О—В—К—А. –£–≤–µ–ї–Є—З–µ–љ–Є–µ—В–Њ –љ–∞ –±—А–Њ—П –љ–∞ –Є—В–µ—А–∞—Ж–Є–Є—В–µ –њ—А–∞–≤–Є —Д—А–∞–Ї—В–∞–ї–Є—В–µ –њ–Њ-—В–Њ—З–љ–Є.
–°—К—Й–µ—Б—В–≤—Г–≤–∞—В —В—А–Є –Њ—Б–љ–Њ–≤–љ–Є –≤–Є–і–∞ –Є—В–µ—А–∞—Ж–Є–Є:
1. –Ч–∞–Љ–µ—Б—В–≤–∞—Й–∞ –Є—В–µ—А–∞—Ж–Є—П - —Б—К–Ј–і–∞–≤–∞ —Д—А–∞–Ї—В–∞–ї–Є, –Ј–∞–Љ–µ–љ—П–є–Ї–Є –µ–і–љ–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є —Д–Є–≥—Г—А–Є —Б –і—А—Г–≥–Є.
2. –Ш—В–µ—А–∞—Ж–Є—П IFS - —Б—К–Ј–і–∞–≤–∞ —Д—А–∞–Ї—В–∞–ї–Є, –њ—А–Є–ї–∞–≥–∞–є–Ї–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є –њ—А–µ–Њ–±—А–∞–Ј—Г–≤–∞–љ–Є—П (—В–Є–њ –Ј–∞–≤—К—А—В–∞–љ–µ –Є –Њ—В—А–∞–ґ–µ–љ–Є–µ).
3. –Ш—В–µ—А–∞—Ж–Є—П —Б —Д–Њ—А–Љ—Г–ї–Є вАФ –≤–Ї–ї—О—З–≤–∞ –љ—П–Ї–Њ–ї–Ї–Њ –љ–∞—З–Є–љ–∞ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ —Д—А–∞–Ї—В–∞–ї–Є, –њ–Њ–≤—В–∞—А—П–є–Ї–Є –љ—П–Ї–∞–Ї–≤–∞ –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–∞ —Д–Њ—А–Љ—Г–ї–∞ –Є–ї–Є –љ—П–Ї–Њ–ї–Ї–Њ —Д–Њ—А–Љ—Г–ї–Є.
–°—К—Й–µ—Б—В–≤—Г–≤–∞—В –Є –і—А—Г–≥–Є¬†–≤–Є–і–Њ–≤–µ –Є—В–µ—А–∞—Ж–Є–Є. –Э–∞–њ—А–Є–Љ–µ—А, —Д—А–∞–Ї—В–∞–ї–Є –Љ–Њ–ґ–µ –і–∞ —Б–µ —Б—К–Ј–і–∞–≤–∞—В¬†–Ї–∞—В–Њ —Б–µ¬†—Б–≥—К–≤–∞ —Е–∞—А—В–Є—П. –Ю–±–∞—З–µ —Б—К—Й–Є—В–µ —В–µ–Ј–Є —Д—А–∞–Ї—В–∞–ї–Є –Љ–Њ–≥–∞—В –і–∞ —Б–µ –Њ–±—А–∞–Ј—Г–≤–∞—В –Є —Б –љ—П–Ї–Њ–Є –Њ—В –Є–Ј–±—А–Њ–µ–љ–Є—В–µ —Б—В–∞–љ–і–∞—А—В–љ–Є –Љ–µ—В–Њ–і–Є.
–Ч–∞–Љ–µ—Б—В–≤–∞—Й–∞ –Є—В–µ—А–∞—Ж–Є—П
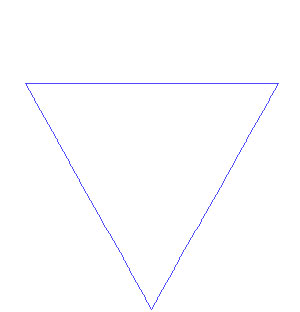
–Ч–∞–њ–Њ—З–≤–∞–Љ–µ —Б —Д–Є–≥—Г—А–∞, –љ–∞—А–µ—З–µ–љ–∞ –Њ—Б–љ–Њ–≤–∞. –°–ї–µ–і —В–Њ–≤–∞ –≤—Б—П–Ї–∞ —З–∞—Б—В –Њ—В –Њ—Б–љ–Њ–≤–∞—В–∞ –Ј–∞–Љ–µ—Б—В–≤–∞–Љ–µ —Б –і—А—Г–≥–∞ —Д–Є–≥—Г—А–∞, –љ–∞—А–µ—З–µ–љ–∞ –Љ–Њ—В–Є–≤. –Ш–Ј–≤—К—А—И–≤–∞–Љ–µ —В–Њ–≤–∞ –Ј–∞–Љ–µ—Б—В–≤–∞–љ–µ –±–µ–Ј–Ї—А–∞–є–љ–Њ –Ї–Њ–ї–Є—З–µ—Б—В–≤–Њ –њ—К—В–Є, –і–Њ–Ї–∞—В–Њ –Ј–∞–≤—К—А—И–Є–Љ —Д—А–∞–Ї—В–∞–ї–∞.
| –Э–∞–њ—А–Є–Љ–µ—А, –і–∞ –Њ–њ–Є—В–∞–Љ–µ –і–∞ –љ–∞–њ—А–∞–≤–Є–Љ —Д—А–∞–Ї—В–∞–ї | —Б —В–∞–Ј–Є –Њ—Б–љ–Њ–≤–∞ |  |
¬†–Є –Љ–Њ—В–Є–≤:¬† |  |
 |
|||||
| 1 | 2 | 3 | 4 | 5 | 6 |
–Ч–∞–њ–Њ—З–≤–∞–є–Ї–Є —Б —В—А–Є—К–≥—К–ї–љ–Є–Ї, –Ј–∞–Љ–µ–љ—П–Љ–µ –≤—Б—П–Ї–∞ –љ–µ–≥–Њ–≤–∞ —Б—В—А–∞–љ–∞ —Б –Љ–Њ—В–Є–≤–∞. –Ю—В–љ–Њ–≤–Њ –Ј–∞–Љ–µ–љ—П–Љ–µ –≤—Б—П–Ї–∞ –Њ—В 12-—В–µ –Њ—В—Б–µ—З–Ї–Є —Б –Љ–Њ—В–Є–≤–∞ –Є –њ—А–Њ–і—К–ї–ґ–∞–≤–∞–Љ–µ –њ—А–Њ—Ж–µ—Б–∞. –Э–∞–Ї—А–∞—П –њ–Њ–ї—Г—З–∞–≤–∞–Љ–µ —Д—А–∞–Ї—В–∞–ї, –љ–∞—А–µ—З–µ–љ –°–љ–µ–ґ–Є–љ–Ї–∞—В–∞ –љ–∞ –Ъ–Њ—Е. –Ь–Њ–ґ–µ –і–∞ —А–∞–Ј–≥–ї–µ–і–∞—В–µ —А–∞–Ј–≤–Є—В–Є–µ—В–Њ –љ–∞ —Д—А–∞–Ї—В–∞–ї–∞ –Ј–∞ –≤—Б–µ–Ї–Є –µ—В–∞–њ¬†–Ї–∞—В–Њ –Љ–Є–љ–µ—В–µ —Б –Љ–Є—И–Ї–∞—В–∞ –њ–Њ –±—Г—В–Њ–љ–Є—В–µ.
–Ґ–∞–Ј–Є —Д–Є–≥—Г—А–∞ –µ –µ–і–Є–љ –Њ—В –њ—К—А–≤–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є –Є–Ј—Б–ї–µ–і–≤–∞–љ–Є –Њ—В —Г—З–µ–љ–Є—В–µ. –Ґ—П —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ –Њ—В —В—А–Є –µ–і–љ–∞–Ї–≤–Є –Ї—А–Є–≤–Є –љ–∞ –Ъ–Њ—Е:
 |
|||
| 1 | 2 | 3 | 4 |
–Ъ—А–Є–≤–∞—В–∞ –љ–∞ –Ъ–Њ—Е¬†—Б–µ –њ–Њ—П–≤—П–≤–∞ –Ј–∞ –њ—К—А–≤–Є –њ—К—В –≤ —Б—В–∞—В–Є—П—В–∞ –љ–∞ —И–≤–µ–і—Б–Ї–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Э–Є–ї—Б –§–∞–±–Є–∞–љ –•–µ–ї–≥–µ —Д–Њ–љ –Ъ–Њ—Е –њ—А–µ–Ј 1904. –Ґ–∞–Ј–Є –Ї—А–Є–≤–∞ –µ –Ј–∞–Љ–Є—Б–ї–µ–љ–∞ –Ї–∞—В–Њ –њ—А–Є–Љ–µ—А –Ј–∞ –љ–µ–њ—А–µ–Ї—К—Б–љ–∞—В–∞ –ї–Є–љ–Є—П, –Ї—К–Љ –Ї–Њ—П—В–Њ –љ–µ –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–µ–Ї–∞—А–∞ –і–Њ–њ–Є—А–∞—В–µ–ї–љ–∞ –≤—К–≤ –≤—Б—П–Ї–∞ —В–Њ—З–Ї–∞. –Ы–Є–љ–Є–Є —Б –њ–Њ–і–Њ–±–љ–Є —Б–≤–Њ–є—Б—В–≤–∞ —Б–∞ –±–Є–ї–Є –Є–Ј–≤–µ—Б—В–љ–Є –Є –њ—А–µ–і–Є (–Ъ–∞—А–ї –Т–∞–є–µ—А—Й—А–∞—Б, 1872 –≥.), –љ–Њ –Ї—А–Є–≤–∞—В–∞ –љ–∞ –Ъ–Њ—Е –µ –Ј–∞–±–µ–ї–µ–ґ–Є—В–µ–ї–љ–∞ —Б –њ—А–Њ—Б—В–Њ—В–∞—В–∞ —Б–Є.¬†
–° —А–∞–Ј–ї–Є—З–љ–Є –Њ—Б–љ–Њ–≤–Є, –Љ–Њ—В–Є–≤–Є –Є –љ–∞—З–Є–љ–Є –љ–∞ –Ј–∞–Љ–µ—Б—В–≤–∞–љ–µ –љ–∞ –Љ–Њ—В–Є–≤–Є—В–µ –Љ–Њ–≥–∞—В –і–∞ —Б–µ –њ–Њ–ї—Г—З–∞—В –Љ–љ–Њ–≥–Њ —А–∞–Ј–љ–Њ–Њ–±—А–∞–Ј–љ–Є —Д—А–∞–Ї—В–∞–ї–Є.¬†
L-—Б–Є—Б—В–µ–Љ–Є
–Ч–∞–Љ–µ—Б—В–≤–∞—Й–∞—В–∞ –Є—В–µ—А–∞—Ж–Є—П –µ –Љ–љ–Њ–≥–Њ –њ—А–Њ—Б—В–∞. –Э–Њ –Ј–∞ –Ї–Њ–Љ–њ—О—В—К—А, –љ–µ –µ –і–Њ—Б—В–∞—В—К—З–љ–Њ –і–∞ –Є–Љ–∞—И –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ—В–Њ –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –Є –Љ–Њ—В–Є–≤–∞. –Э–µ–Њ–±—Е–Њ–і–Є–Љ –µ —П—Б–µ–љ –Є —В–Њ—З–µ–љ –љ–∞—З–Є–љ –Ј–∞ —Б—К—Е—А–∞–љ–µ–љ–Є–µ –љ–∞ –і–∞–љ–љ–Є—В–µ –Ј–∞ —Д—А–∞–Ї—В–∞–ї–Є—В–µ, –Ї–Њ–є—В–Њ –і–∞ –њ–Њ–Ј–≤–Њ–ї—П–≤–∞ –і–∞ —Б–µ —Б—К–Ј–і–∞–≤–∞—В –њ—А–Њ—Б—В–Є –∞–ї–≥–Њ—А–Є—В–Љ–Є –Ј–∞ –Є–Ј—З–µ—А—В–∞–≤–∞–љ–µ –љ–∞ —Д—А–∞–Ї—В–∞–ї–Є.
–Х–і–Є–љ –і–Њ–±—К—А –Є –њ—А–Њ—Б—В –љ–∞—З–Є–љ —Б–∞ L-—Б–Є—Б—В–µ–Љ–Є—В–µ. –†–∞–Ј—А–∞–±–Њ—В–µ–љ–Є —Б–∞ –Њ—В –Р. –Ы–Є–љ–і–µ–љ–Љ–∞–є–µ—А ("L" –≤ –і—Г–Љ–∞—В–∞ "L-—Б–Є—Б—В–µ–Љ–∞" ). –Ґ–µ —Б–∞ —Б—К—Б—В–∞–≤–µ–љ–Є –Њ—В —К–≥—К–ї, –∞–Ї—Б–Є–Њ–Љ–∞ –Є –њ–Њ–љ–µ –µ–і–љ–Њ –њ—А–∞–≤–Є–ї–Њ. –Р–Ї—Б–Є–Њ–Љ–∞¬†–љ–∞—А–Є—З–∞–Љ–µ –љ–∞—З–∞–ї–љ–∞—В–∞ —Д–Њ—А–Љ–∞ (–Њ—Б–љ–Њ–≤–∞), –Ї–Њ—П—В–Њ —Й–µ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞ –≤ –њ—А–Њ—Ж–µ—Б–∞ –љ–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ —Д—А–∞–Ї—В–∞–ї–∞. –Я—А–∞–≤–Є–ї–∞—В–∞ —Г–Ї–∞–Ј–≤–∞—В, –Ї–∞–Ї–≤–Є —Б–Є–Љ–≤–Њ–ї–Є –≤ –∞–Ї—Б–Є–Њ–Љ–∞—В–∞ —В—А—П–±–≤–∞ –і–∞ –±—К–і–∞—В –Ј–∞–Љ–µ–љ–µ–љ–Є —Б –і—А—Г–≥–Є —Б–Є–Љ–≤–Њ–ї–Є.
| –°–Ш–Ь–Т–Ю–Ы–Ш | ||||||
| –Ю–±—Й–Є —Б–Є–Љ–≤–Њ–ї–Є | –°–ї–Њ–ґ–љ–Є —Б–Є–Љ–≤–Њ–ї–Є | –°–Є–Љ–≤–Њ–ї–Є –Ј–∞ —Ж–≤–µ—В—П–≤–∞–љ–µ | ||||
| F | –Ф–≤–Є–ґ–µ–љ–Є–µ –љ–∞–њ—А–µ–і, —Б—К—Б —Б–ї–µ–і–∞ | @n | –Ф–∞ —Б–µ —Г–Љ–љ–Њ–ґ–Є –і—К–ї–ґ–Є–љ–∞—В–∞ –љ–∞ –Њ—В—Б–µ—З–Ї–∞—В–∞ –љ–∞ n | Cn | –Ф–∞ —Б–µ —Г—Б—В–∞–љ–Њ–≤–Є —Ж–≤—П—В –љ–Њ–Љ–µ—А n | |
| G | –Ф–≤–Є–ґ–µ–љ–Є–µ –љ–∞–њ—А–µ–і, –±–µ–Ј —Б–ї–µ–і–∞ | I | –Я—А–µ–і —З–Є—Б–ї–Њ –Њ–Ј–љ–∞—З–∞–≤–∞ –і–µ–ї–µ–љ–µ –≤–Љ–µ—Б—В–Њ —Г–Љ–љ–Њ–ґ–µ–љ–Є–µ | <n | –Ф–∞ —Б–µ –љ–∞–Љ–∞–ї–Є –љ–Њ–Љ–µ—А–∞ –љ–∞ —Ж–≤–µ—В–∞ —Б n | |
| + | –Ч–∞–≤—К—А—В–∞–љ–µ –њ—А–Њ—В–Є–≤ —З–∞—Б–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ | Q | –Я—А–µ–і —З–Є—Б–ї–Њ –і–∞–≤–∞ –Ї–≤–∞–і—А–∞—В–µ–љ –Ї–Њ—А–µ–љ | >n | –Ф–∞ —Б–µ —Г–≤–µ–ї–Є—З–Є –љ–Њ–Љ–µ—А–∞ –љ–∞ —Ж–≤–µ—В–∞ —Б n | |
| - | –Ч–∞–≤—К—А—В–∞–љ–µ –њ–Њ —З–∞—Б–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ | ! | –Я—А–Њ–Љ–µ–љ—П –Ј–љ–∞–Ї–∞ –Њ—В + –љ–∞ - | |||
| | | –Ч–∞–≤—К—А—В–∞–љ–µ –љ–∞ 180 –Њ | [ | –Ф–∞ —Б–µ –≤–Ї–∞—А–∞ —Б–µ–≥–∞—И–љ–∞—В–∞ –њ–Њ–Ј–Є—Ж–Є—П—В–∞ –љ–∞ –Ї—Г—А—Б–Њ—А–∞ –≤ –њ–∞–Љ–µ—В—В–∞ | |||
| ] | –Ф–∞ —Б–µ –Є–Ј–≤–∞–і–Є –њ–Њ—Б–ї–µ–і–љ–∞—В–∞ –Ј–∞–њ–Є—Б–∞–љ–∞ –њ–Њ–Ј–Є—Ж–Є—П –љ–∞ –Ї—Г—А—Б–Њ—А–∞ –Њ—В –њ–∞–Љ–µ—В—В–∞ | |||||
–°—К—Й–љ–Њ—Б—В—В–∞ –љ–∞ L-–Ї–Њ–і–Є—А–∞–љ–µ—В–Њ –µ –њ—А–Њ—Б—В–∞:
–Я—А–µ–і—Б—В–∞–≤–µ—В–µ —Б–Є –њ—А–Њ–≥—А–∞–Љ–Є—А—Г–µ–Љ–Њ —Г—Б—В—А–Њ–є—Б—В–≤–Њ, –Њ—В –њ–Є—Б–µ—Ж, –Ї–Њ–љ—В—А–Њ–ї–Є—А–∞—Й –Љ–µ—Е–∞–љ–Є–Ј—К–Љ –Є –ї–Є—Б—В —Е–∞—А—В–Є—П. –£–њ—А–∞–≤–ї—П–≤–∞—Й–Є—П—В –Љ–µ—Е–∞–љ–Є–Ј—К–Љ –љ–∞ –њ–Є—Б–µ—Ж–∞ –Є–Љ–∞ –љ–∞–±–Њ—А –Њ—В –љ—П–Ї–Њ–ї–Ї–Њ –Ї–Њ–Љ–∞–љ–і–Є:
- –і–∞ —Б–Љ—К–Ї–љ–µ –њ–Є—Б–∞–ї–Ї–∞—В–∞ –≤—К—А—Е—Г —Е–∞—А—В–Є—П—В–∞
- –і–∞ –љ–∞—З–µ—А—В–∞–µ –Њ—В—Б–µ—З–Ї–∞ —Б –і–∞–і–µ–љ–∞ –і—К–ї–ґ–Є–љ–∞ —Б –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ –љ–∞ —В–µ–Ї—Г—Й–∞—В–∞ –Њ—А–Є–µ–љ—В–∞—Ж–Є—П –љ–∞ –њ–Є—Б–∞–ї–Ї–∞—В–∞ (–Ї–Њ–Љ–∞–љ–і–∞ F).
- –і–∞ –њ—А–Њ–Љ–µ–љ–Є –Њ—А–Є–µ–љ—В–∞—Ж–Є—П—В–∞ –љ–∞ –њ–Є—Б–∞–ї–Ї–∞ —Б–њ—А—П–Љ–Њ —В–µ–Ї—Г—Й–∞—В–∞ –љ–∞ –і–∞–і–µ–љ –Њ—В–љ–Њ—Б–Є—В–µ–ї–µ–љ —К–≥—К–ї —Б–њ—А—П–Љ–Њ —З–∞—Б–Њ–≤–љ–Є–Ї–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ –Є–ї–Є –Њ–±—А–∞—В–љ–Њ –љ–∞ —З–∞—Б–Њ–≤–љ–Є–Ї–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ (–Ї–Њ–Љ–∞–љ–і–∞ + –Є -).
- –і–∞ –Ј–∞–њ–Њ–Љ–љ–Є (–≤–Ї–∞—А–≤–∞ –≤ —Б—В–µ–Ї–∞) —В–µ–Ї—Г—Й–Њ—В–Њ —Б—К—Б—В–Њ—П–љ–Є–µ (–Ї–Њ–Љ–∞–љ–і–∞ [) –Є –і–∞ —Б–Є —Б–њ–Њ–Љ–љ–Є (–і–∞ –Є–Ј–≤–∞–і–Є –Њ—В —Б—В–µ–Ї–∞) –њ—А–µ–і–≤–∞—А–Є—В–µ–ї–љ–Њ –Ј–∞–њ–∞–Љ–µ—В–µ–љ–Њ —Б—К—Б—В–Њ—П–љ–Є–µ (–Ї–Њ–Љ–∞–љ–і–∞ ]).
–Я–Њ–і —Б—К—Б—В–Њ—П–љ–Є–µ —Б–µ —А–∞–Ј–±–Є—А–∞—В —В—А–Є—В–µ —З–Є—Б–ї–∞ (x, y, a), –Ї—К–і–µ—В–Њ x –Є y —Б–∞ –Ї–Њ–Њ—А–і–Є–љ–∞—В–Є—В–µ –љ–∞ –њ–Є—Б–∞–ї–Ї–∞—В–∞, –∞ a –µ —К–≥—К–ї—К—В, –Ї–Њ–є—В–Њ –Њ–њ—А–µ–і–µ–ї—П –њ–Њ—Б–Њ–Ї–∞—В–∞ –љ–∞ –Њ—А–Є–µ–љ—В–∞—Ж–Є—П –љ–∞ –њ–Є—Б–∞–ї–Ї–∞—В–∞. –Я–Њ —В–Њ–Ј–Є –љ–∞—З–Є–љ, –Ј–∞–і–∞–≤–∞–є–Ї–Є –љ—П–Ї–∞–Ї–≤–∞ –њ—К—А–≤–Њ–љ–∞—З–∞–ї–љ–∞ –њ–Њ—Б–Њ–Ї–∞ a0 , —К–≥—К–ї –љ–∞ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Њ –Ј–∞–≤—К—А—В–∞–љ–µ –Њ—В 900 –Є –і—К–ї–ґ–Є–љ–∞—В–∞ –љ–∞ –Њ—В—Б–µ—З–Ї–∞—В–∞, –Ї–∞—В–Њ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ—Б—В—В–∞ –Њ—В –Ї–Њ–Љ–∞–љ–і–Є, F + F + F + F, –Љ–Њ–ґ–µ–Љ –і–∞ –љ–∞—З–µ—А—В–∞–µ–Љ –Ї–≤–∞–і—А–∞—В. –Р–Ї–Њ –Њ–њ—А–µ–і–µ–ї–Є–Љ –Њ—В–љ–Њ—Б–Є—В–µ–ї–љ–Є—П —К–≥—К–ї –љ–∞ –Ј–∞–≤—К—А—В–∞–љ–µ –љ–∞ 600, –Є–Ј–њ–Њ–ї–Ј–≤–∞–є–Ї–Є —Б–µ—А–Є—П—В–∞ –Њ—В –Ї–Њ–Љ–∞–љ–і–Є F ++ F ++ F —Й–µ –љ–∞—З–µ—А—В–∞–µ–Љ –µ–і–Є–љ —А–∞–≤–љ–Њ—Б—В—А–∞–љ–µ–љ —В—А–Є—К–≥—К–ї–љ–Є–Ї.
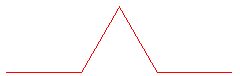
| –Х—В–Њ –Њ—Й–µ –µ–і–Є–љ –њ—А–Є–Љ–µ—А, –°–љ–µ–ґ–Є–љ–Ї–∞—В–∞ –љ–∞ –Ъ–Њ—Е, –Ґ—П –Є–Ј–њ–Њ–ї–Ј–≤–∞ —Б–ї–µ–і–љ–∞—В–∞ | –Њ—Б–љ–Њ–≤–∞ |  |
¬†–Є –Љ–Њ—В–Є–≤:¬† |  |
–Ш–Ј–њ–Њ–ї–Ј–≤–∞–є–Ї–Є L-—Б–Є—Б—В–µ–Љ–∞, –Љ–Њ–ґ–µ–Љ –і–∞ –Ј–∞–њ–Є—И–µ–Љ –°–љ–µ–ґ–Є–љ–Ї–∞—В–∞ –љ–∞ –Ъ–Њ—Е –њ–Њ —Б–ї–µ–і–љ–Є—П –љ–∞—З–Є–љ:
|
Koch { Angle 60 |
L-—Б–Є—Б—В–µ–Љ–∞—В–∞ –Ј–∞–њ–Њ—З–≤–∞ —Б –љ–∞–Ј–≤–∞–љ–Є–µ—В–Њ, —Б–ї–µ–і–≤–∞ —Б–Ї–Њ–±–∞ ; —В–Њ–≤–∞ –µ —К–≥—К–ї–∞, –љ–∞ –Ї–Њ–є—В–Њ —Б–µ –Њ—В–Ї–ї–Њ–љ—П–≤–∞ –ї–Є–љ–Є—П—В–∞ –љ–∞ —Д—А–∞–Ї—В–∞–ї–∞; —В—А–Є —Б—В—А–∞–љ–Є —Б –і–≤–µ –Ј–∞–≤—К—А—В–∞–љ–Є—П –њ–Њ —З–∞—Б–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ –љ–∞ 120 –≥—А–∞–і—Г—Б–∞; –≤—Б—П–Ї–∞ —Б—В—А–∞–љ–∞ —Б–µ –Ј–∞–Љ–µ–љ—П —Б –Љ–Њ—В–Є–≤–∞ (F +F- -F + F); —Б–Ї–Њ–±–∞—В–∞ –Њ–Ј–љ–∞—З–∞–≤–∞ –њ–Њ–≤—В–Њ—А–µ–љ–Є–µ |
–Я–Њ–≤–µ—З–µ—В–Њ —Д—А–∞–Ї—В–∞–ї–Є —Б —Д—А–∞–Ї—В–∞–ї–љ–∞ —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В –Њ—В 0 –і–Њ 2 –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –Є–Ј—А–∞–Ј–µ–љ–Є –Ї–∞—В–Њ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В L-—Б–Є—Б—В–µ–Љ–Є. –° –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П –Њ—В –љ—П–Ї–Њ–ї–Ї–Њ —Б–Є–Љ–≤–Њ–ї–∞ –Є –њ—А–∞–≤–Є–ї–∞ –Љ–Њ–≥–∞—В –і–∞ —Б–µ —Б—К–Ј–і–∞–і–∞—В –Љ–љ–Њ–≥–Њ —Б–ї–Њ–ґ–љ–Є —Д—А–∞–Ї—В–∞–ї–Є. –Ґ–∞–Ї–Є–≤–∞ L-—Б–Є—Б—В–µ–Љ–Є —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В, –Ј–∞ –і–∞ —Б–µ —Б—К–Ј–і–∞–≤–∞—В —А–µ–∞–ї–Є—Б—В–Є—З–љ–Є –Љ–Њ–і–µ–ї–Є –љ–∞ —А–∞—Б—В–µ–љ–Є—П.
  |
  |
  |
| F = FF-[-F+F+F]+[+F-F-F] |
X -> F-[[X]+X]+F[+FX]-X |
F= G[+F][-F]GF |
–Т—К–Ј–Љ–Њ–ґ–љ–Њ –µ –і–∞ —Б–µ –њ–Њ—Б—В–Є–≥–љ–µ –Є –њ–Њ-–≥–Њ–ї—П–Љ —А–µ–∞–ї–Є–Ј—К–Љ –Ї–∞—В–Њ —Б–µ –≤–љ–µ—Б–µ –њ–∞—А–∞–Љ–µ—В—К—А,¬†–і–Њ–±–∞–≤—П—Й —Б–ї—Г—З–∞–є–љ–Є —З–Є—Б–ї–∞. –Ъ–Њ–ї–Ї–Њ—В–Њ –µ –њ–Њ-–≥–Њ–ї—П–Љ –і–Є–∞–њ–∞–Ј–Њ–љ–∞ –Є–Љ, —В–Њ–ї–Ї–Њ–≤–∞ —Д–Њ—А–Љ–Є—В–µ —Й–µ –Є–Ј–≥–ї–µ–ґ–і–∞—В –њ–Њ-–µ—Б—В–µ—Б—В–≤–µ–љ–Є –Є –і–∞–ї–µ—З–µ –Њ—В —Б–Є–Љ–µ—В—А–Є—П—В–∞.
 |
 |
 |
 |
 |
 |
–°–Є—Б—В–µ–Љ–Є –Ш—В–µ—А–∞—В–Є–≤–љ–Є –§—Г–љ–Ї—Ж–Є–Є (Iterated Functions System - IFS)
IFS (–Є—В–µ—А–∞—В–Є–≤–љ–Є —Д—Г–љ–Ї—Ж–Є–Њ–љ–∞–ї–љ–Є —Б–Є—Б—В–µ–Љ–Є) –њ—А–µ–і—Б—В–∞–≤—П—В –Њ—Й–µ –µ–і–Є–љ –љ–∞—З–Є–љ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ —Д—А–∞–Ї—В–∞–ї–Є. –Ґ–Њ–Ј–Є –Љ–µ—В–Њ–і –µ –Њ—Б–љ–Њ–≤–∞–љ –љ–∞ —В–Њ—З–Ї–∞ –Є–ї–Є —Д–Є–≥—Г—А–∞, –Ї–Њ—П—В–Њ —Б–µ –Ј–∞–Љ–µ–љ—П —Б –љ—П–Ї–Њ–ї–Ї–Њ –њ–Њ-–Љ–∞–ї–Ї–Є —Д–Є–≥—Г—А–Є.
–Э–∞–њ—А–Є–Љ–µ—А, —Б—К—Й–µ—Б—В–≤—Г–≤–∞ –Љ–љ–Њ–≥–Њ –њ—А–Њ—Б—В –љ–∞—З–Є–љ –Ј–∞ –Є–Ј—З–µ—А—В–∞–≤–∞–љ–µ –љ–∞ –Ґ—А–Є—К–≥—К–ї–љ–Є–Ї–∞ –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є. –Ч–∞–њ–Њ—З–≤–∞–є–Ї–Є —Б —В—А–Є—К–≥—К–ї–љ–Є–Ї, –Ј–∞–Љ–µ–љ—П–Љ–µ¬†–≥–Њ —Б —В—А–Є –Љ–∞–ї–Ї–Є —В—А–Є—К–≥—К–ї–љ–Є—Ж–Є: –Я—А–Њ–і—К–ї–ґ–∞–≤–∞–є–Ї–Є —В–Њ–Ј–Є –њ—А–Њ—Ж–µ—Б –љ–∞ –Є—В–µ—А–∞—Ж–Є—П, –љ–Є–µ –Ј–∞–Љ–µ–љ—П–Љ–µ –≤—Б–µ–Ї–Є –Њ—В —В–µ–Ј–Є —В—А–Є —В—А–Є—К–≥—К–ї–љ–Є–Ї–∞ —Б –і—А—Г–≥–Є —В—А–Є—К–≥—К–ї–љ–Є—Ж–Є –Є –њ—А–Њ–і—К–ї–ґ–∞–≤–∞–Љ–µ –Љ–љ–Њ–≥–Њ –њ—К—В–Є: –і–Њ–Ї–∞—В–Њ —Б—В–Є–≥–љ–µ–Љ –і–Њ:
–і–Њ–Ї–∞—В–Њ —Б—В–Є–≥–љ–µ–Љ –і–Њ:
–Ч–∞–Љ—П–љ–∞—В–∞ –љ–∞ –µ–і–љ–∞ —Д–Њ—А–Љ–∞ —Б –і—А—Г–≥–∞ —Д–Њ—А–Љ–∞ —Б–µ –љ–∞—А–Є—З–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Њ –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ .
–Т –≥–Њ—А–љ–Є—П –њ—А–Є–Љ–µ—А –Є–Љ–∞ –і–≤–∞ –≤–Є–і–∞ –њ—А–µ–Њ–±—А–∞–Ј—Г–≤–∞–љ–Є—П: —В—А–∞–љ—Б–ї–∞—Ж–Є—П (–і–≤–Є–ґ–µ–љ–Є–µ –љ–∞ —В—А–Є—К–≥—К–ї–љ–Є—Ж–Є—В–µ) –Є –Є–Ј–Љ–µ–љ–µ–љ–Є–µ –љ–∞ —А–∞–Ј–Љ–µ—А–∞ –љ–∞ —В—А–Є—К–≥—К–ї–љ–Є—Ж–Є—В–µ.
–Ґ—А–µ—В–Є—П—В –≤–Є–і –њ—А–µ–Њ–±—А–∞–Ј–Њ–≤–∞–љ–Є–µ –µ –≤—К—А—В–µ–љ–µ—В–Њ. –Ґ–Њ –Љ–Њ–ґ–µ –і–∞ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞ –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ —Д—А–∞–Ї—В–∞–ї–Є, –≤ –Ї–Њ–Є—В–Њ —Б–∞–Љ–Њ–њ–Њ–і–Њ–±–љ–Є—В–µ —З–∞—Б—В–Є —Б–∞ —А–∞–Ј–Љ–µ—Б—В–µ–љ–Є –њ–Њ–і —А–∞–Ј–ї–Є—З–љ–Є —К–≥–ї–Є. –Э–∞–њ—А–Є–Љ–µ—А, –Ј–∞ –і–∞ —Б–µ —Б—К–Ј–і–∞–і–µ —А–µ–∞–ї–Є—Б—В–Є—З–µ–љ –Љ–Њ–і–µ–ї –љ–∞ –і—К—А–≤–Њ, –Є–Љ–∞ –љ—Г–ґ–і–∞ –Њ—В –≤—К—А—В–µ–љ–µ—В–Њ –Ј–∞ –Ї–ї–Њ–љ–Є—В–µ.
–Ф—А—Г–≥–Є—В–µ –≤–Є–і–Њ–≤–µ –њ—А–µ–Њ–±—А–∞–Ј—Г–≤–∞–љ–Є—П, —В–Є–њ –Њ–≥–ї–µ–і–∞–ї–љ–Њ –Њ—В—А–∞–ґ–µ–љ–Є–µ –Є –Є–љ–≤–µ—А—Б–Є—П –Љ–Њ–≥–∞—В –і–∞ —Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В –Ј–∞ —Б—К–Ј–і–∞–≤–∞–љ–µ –љ–∞ –Њ–≥—А–Њ–Љ–љ–Њ —А–∞–Ј–љ–Њ–Њ–±—А–∞–Ј–Є–µ –Њ—В —Д—А–∞–Ї—В–∞–ї–Є. IFS –Ј–љ–∞—З–Є—В–µ–ї–љ–Њ –Њ–±–ї–µ–Ї—З–∞–≤–∞—В –∞–ї–≥–Њ—А–Є—В–Љ–Є—В–µ –Ј–∞ –Є–Ј—З–µ—А—В–∞–≤–∞–љ–µ –љ–∞ —Д—А–∞–Ї—В–∞–ї–Є—В–µ. –Ч–∞ –і–≤—Г–Љ–µ—А–љ–Є —Д—А–∞–Ї—В–∞–ї–Є –≤—Б–Є—З–Ї–Њ, –Ї–Њ–µ—В–Њ —В—А—П–±–≤–∞ –і–∞ —Б–ї–Њ–ґ–Є—В–µ –≤ –њ–∞–Љ–µ—В—В–∞ –љ–∞ –Ї–Њ–Љ–њ—О—В—К—А–∞, –µ —Б–њ–Є—Б—К–Ї —Б –≤—Б–Є—З–Ї–Є –њ—А–µ–Њ–±—А–∞–Ј—Г–≤–∞–љ–Є—П —Б 6 –њ–∞—А–∞–Љ–µ—В—А–Є –Ј–∞ –≤—Б—П–Ї–Њ.
X' = A*X + B*Y + C
Y' = D*X + E*Y + F
- –•–Њ—А–Є–Ј–Њ–љ—В–∞–ї–љ–Њ –і–≤–Є–ґ–µ–љ–Є–µ
- –Т–µ—А—В–Є–Ї–∞–ї–љ–Њ –і–≤–Є–ґ–µ–љ–Є–µ
- –Т—К—А—В–µ–љ–µ –Њ–Ї–Њ–ї–Њ –≤–µ—А—В–Є–Ї–∞–ї–љ–∞—В–∞ –Њ—Б –љ–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ—В–Њ
- –Т—К—А—В–µ–љ–µ –Њ–Ї–Њ–ї–Њ —Е–Њ—А–Є–Ј–Њ–љ—В–∞–ї–љ–∞—В–∞ –Њ—Б –љ–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ—В–Њ
- –Ь–∞—Й–∞–±–Є—А–∞–љ–µ –њ–Њ –≤–µ—А—В–Є–Ї–∞–ї–љ–∞—В–∞ –Њ—Б –љ–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ—В–Њ
- –Ь–∞—Й–∞–±–Є—А–∞–љ–µ –њ–Њ —Е–Њ—А–Є–Ј–Њ–љ—В–∞–ї–љ–∞—В–∞ –Њ—Б –љ–∞ –Є–Ј–Њ–±—А–∞–ґ–µ–љ–Є–µ—В–Њ.
–Ч–∞ 3-–Љ–µ—А–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є —Б–∞ –љ–µ–Њ–±—Е–Њ–і–Є–Љ–Є –і–Њ–њ—К–ї–љ–Є—В–µ–ї–љ–Њ –Њ—Й–µ 3 –њ–∞—А–∞–Љ–µ—В—К—А–∞ –Ј–∞ —В—А–µ—В–∞—В–∞ –Њ—Б. ¬†
–Я–Њ–≤–µ—З–µ –њ–Њ–і—А–Њ–±–љ–Њ—Б—В–Є - –≤ ¬†—В–µ–Љ–∞—В–∞:¬†–°–Є—Б—В–µ–Љ–Є –Ш—В–µ—А–∞—В–Є–≤–љ–Є –§—Г–љ–Ї—Ж–Є–Є (Iterated Functions System - IFS)
–§–Њ—А–Љ—Г–ї–љ–∞ –Є—В–µ—А–∞—Ж–Є—П
–§–Њ—А–Љ—Г–ї–љ–∞—В–∞ –Є—В–µ—А–∞—Ж–Є—П –µ –љ–∞–є-–њ—А–Њ—Б—В–Є—П –≤–Є–і –Є—В–µ—А–∞—Ж–Є—П, –љ–Њ –µ –љ–∞–є-–≤–∞–ґ–љ–Є—П –Є –і–∞–≤–∞ –љ–∞–є-—Б–ї–Њ–ґ–љ–Є —А–µ–Ј—Г–ї—В–∞—В–Є. –Р–ї–≥–µ–±—А–Є—З–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є —Б–µ –њ–Њ—Б—В—А–Њ—П–≤–∞—В —З—А–µ–Ј —Д–Њ—А–Љ—Г–ї–љ–∞ –Є—В–µ—А–∞—Ж–Є—П, —В.–µ. —З—А–µ–Ј –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Є —Д–Њ—А–Љ—Г–ї–Є. –©–µ –≥–Є —А–∞–Ј–≥–ї–µ–і–∞–Љ–µ –≤ —В–µ–Љ–∞—В–∞ –Ј–∞ –Р–ї–≥–µ–±—А–Є—З–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є.
–Ю—Б–љ–Њ–≤–љ–Є –њ–Њ–љ—П—В–Є—П –Є –ї–µ–Ї—Б–Є–Ї–∞
- –§—А–∞–Ї—В–∞–ї–Є
- –і—К—А–≤–Њ –љ–∞ –Я–Є—В–∞–≥–Њ—А
- —Б–љ–µ–ґ–Є–љ–Ї–∞ –љ–∞ –Ъ–Њ—Е
- –Ї—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е
- —В—А–Є—К–≥—К–ї–љ–Є–Ї –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є
- –Ш—В–µ—А–∞—Ж–Є—П
- –≤¬†–њ—А–Њ–≥—А–∞–Љ–Є—А–∞–љ–µ—В–Њ
- –≤ –њ–Њ—Б—В—А–Њ—П–≤–∞–љ–µ—В–Њ –љ–∞¬†—Д—А–∞–Ї—В–∞–ї–Є
- –Ч–∞–Љ–µ—Б—В–≤–∞—Й–∞ –Є—В–µ—А–∞—Ж–Є—П
- L-—Б–Є—Б—В–µ–Љ–Є
- –Ш—В–µ—А–∞—Ж–Є—П IFS
- –Ш—В–µ—А–∞—Ж–Є—П —Б —Д–Њ—А–Љ—Г–ї–Є
- –Э–Є–ї—Б –§–∞–±–Є–∞–љ –•–µ–ї–≥–µ —Д–Њ–љ –Ъ–Њ—Е
- –Т–∞—Ж–ї–∞–≤ –§—А–∞–љ—Ж–Є—Б–Ї –°–µ—А–њ–Є–љ—Б–Ї–Є
- –С–µ–љ–Њ–∞ –Ь–∞–љ–і–µ–ї–±—А–Њ—В
–Ш–Ј—В–Њ—З–љ–Є—Ж–Є:
–§—А–∞–Ї—В–∞–ї—М–љ–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П –њ—А–Є—А–Њ–і—Л, –Ь–∞–љ–і–µ–ї—М–±—А–Њ—В –С.
–§—А–∞–Ї—В–∞–ї—М–љ—Л–є —А–Њ—Б—В,¬†–Ы.–Ь. –°–∞–љ–і–µ—А (doc)
–Ю–≥—А–∞–љ–Є—З–µ–љ–љ–∞—П –і–Є—Д—Д—Г–Ј–Є—П
–Я—А–Є–љ—Ж–Є–њ –Ъ—О—А–Є –Є –Њ–≥—А–∞–љ–Є—З–µ–љ–љ–∞—П¬†–і–Є—Д—Д—Г–Ј–Є–µ–є –∞–≥—А–µ–≥–∞—Ж–Є—П¬†¬© –Ы.–Ь. –Ь–∞—А—В—О—И–µ–≤, –Ы.–У. –У–Њ—А–±–Є—З


























–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
–Э—П–Љ–∞ –Ї–Њ–Љ–µ–љ—В–∞—А–Є –Ї—К–Љ —В–∞–Ј–Є –љ–Њ–≤–Є–љ–∞ !
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
4I4ATA
–Э–Њ–≤, —Б–Ї—А–Є—В –і–Њ—Б–µ–≥–∞ –≤—Е–Њ–і –≤ –њ–Є—А–∞–Љ–Є–і–∞—В–∞ –љ–∞ –Ь–Є–Ї–µ—А–Є–љ –µ –Њ—В–Ї—А–Є—В –њ–Њ –∞–љ–Њ–Љ–∞–ї–Є–Є –њ—А–Є —Б–Ї–∞–љ–Є—А–∞–љ–µ
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews