

–У–µ–Њ–Љ–µ—В—А–Є—З–љ–Є —Д—А–∞–Ї—В–∞–ї–Є
–У–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є —Б–∞ –Є–Ј–≤–µ—Б—В–љ–Є –Њ—Й–µ —Б –Є–Љ–µ—В–Њ –і–µ—В–µ—А–Љ–Є–љ–Є—А–∞–љ–Є, —В.–µ. –Њ–њ—А–µ–і–µ–ї–µ–љ–Є —Д—А–∞–Ї—В–∞–ї–Є. –Э–∞—А–Є—З–∞—В –≥–Є –Њ—Й–µ –ї–Є–љ–µ–є–љ–Є –Є–ї–Є –Ї–ї–∞—Б–Є—З–µ—Б–Ї–Є —Д—А–∞–Ї—В–∞–ї–Є, –Ј–∞—Й–Њ—В–Њ –Љ–∞—В–µ–Љ–∞—В–Є—Ж–Є—В–µ —Б–∞ —Б—В–Є–≥–љ–∞–ї–Є –њ—К—А–≤–Њ –і–Њ —В—П—Е.
–Ґ–µ–Ј–Є —Д—А–∞–Ї—В–∞–ї–Є —Б–∞ –ї–µ—Б–љ–Є –Ј–∞ –њ–Њ—Б—В—А–Њ—П–≤–∞–љ–µ –Є –±—Г–Ї–≤–∞–ї–љ–Њ –≤—Б–µ–Ї–Є –Љ–Њ–ґ–µ –і–∞ –љ–∞—З–µ—А—В–∞–µ —В–∞–Ї—К–≤ —Д—А–∞–Ї—В–∞–ї –≤—К—А—Е—Г –Ї–∞—А–Є—А–∞–љ –ї–Є—Б—В. –Ґ–µ–Ј–Є —Д—А–∞–Ї—В–∞–ї–Є —Б–µ –Њ–±—А–∞–Ј—Г–≤–∞—В —Б –Є—В–µ—А–∞—Ж–Є–Є, –Ј–∞ –Ї–Њ–Є—В–Њ –њ–Њ-–њ–Њ–і—А–Њ–±–љ–Њ –µ –Њ–±—П—Б–љ–µ–љ–Њ —В—Г–Ї.
–Т –і–≤—Г–Љ–µ—А–љ–Є—П —Б–ї—Г—З–∞–є —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞—В —Б –њ–Њ–Љ–Њ—Й—В–∞ –љ–∞ –љ—П–Ї–∞–Ї–≤–∞ –љ–∞—З—Г–њ–µ–љ–∞ –ї–Є–љ–Є—П (–Є–ї–Є –њ–Њ–≤—К—А—Е–љ–Њ—Б—В –≤ —В—А–Є–Љ–µ—А–љ–Є—П —Б–ї—Г—З–∞–є), –љ–∞—А–µ—З–µ–љ–∞ –Њ—Б–љ–Њ–≤–∞ (–≥–µ–љ–µ—А–∞—В–Њ—А). –Ч–∞ –≤—Б—П–Ї–∞ —Б—В—К–њ–Ї–∞ –Њ—В –∞–ї–≥–Њ—А–Є—В—К–Љ–∞ (—В.–µ. –Ј–∞ –≤—Б—П–Ї–∞ –Є—В–µ—А–∞—Ж–Є—П) –≤—Б—П–Ї–∞ –Њ—В –Њ—В—Б–µ—З–Ї–Є—В–µ, —Б—К—Б—В–∞–≤—П—Й–Є –љ–∞—З—Г–њ–µ–љ–∞—В–∞ –ї–Є–љ–Є—П, —Б–µ –Ј–∞–Љ–µ–љ—П —Б –≥–µ–љ–µ—А–∞—В–Њ—А–∞, –≤ —Б—К–Њ—В–≤–µ—В–љ–Є—П –Љ–∞—Й–∞–±. –Т —А–µ–Ј—Г–ї—В–∞—В –љ–∞ –±–µ–Ј–Ї—А–∞–є–љ–Є –њ–Њ–≤—В–Њ—А–µ–љ–Є—П (–Є—В–µ—А–∞—Ж–Є–Є) –љ–∞ —В–∞–Ј–Є –њ—А–Њ—Ж–µ–і—Г—А–∞, —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—П —Д—А–∞–Ї—В–∞–ї.
–Ф–∞ —А–∞–Ј–≥–ї–µ–і–∞–љ–µ –љ—П–Ї–Њ–Є –њ–Њ-–Є–Ј–≤–µ—Б—В–љ–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є —Д—А–∞–Ї—В–∞–ї–Є:
–°–љ–µ–ґ–Є–љ–Ї–∞ (–Ї—А–Є–≤–∞) –љ–∞ –Ъ–Њ—Е
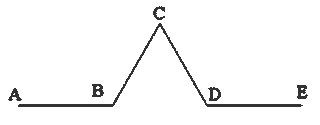 –Р–Ї–Њ k=BD/AB=1 —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ –Ї—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е –≤–∞—А–Є–∞–љ—В 1. –Р–Ї–Њ BD=0 (k=0) —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ –Ї—А–Є–≤–∞—В–∞ –љ–∞ –¶–µ–Ј–∞—А–Њ (–≤–∞—А.2), –∞ –њ—А–Є k=0.2 - –≤–∞—А.3 –Р–Ї–Њ k=BD/AB=1 —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ –Ї—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е –≤–∞—А–Є–∞–љ—В 1. –Р–Ї–Њ BD=0 (k=0) —Б–µ –њ–Њ–ї—Г—З–∞–≤–∞ –Ї—А–Є–≤–∞—В–∞ –љ–∞ –¶–µ–Ј–∞—А–Њ (–≤–∞—А.2), –∞ –њ—А–Є k=0.2 - –≤–∞—А.3 |
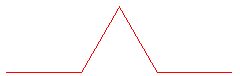
–Т–µ—З–µ —Б–њ–Њ–Љ–µ–љ–∞–≤–∞–љ–∞—В–∞ –Ї—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е –µ –µ–і–Є–љ –Њ—В –љ–∞–є-—В–Є–њ–Є—З–љ–Є—В–µ –і–µ—В–µ—А–Љ–Є–љ–Є—А–∞–љ–Є —Д—А–∞–Ї—В–∞–ї–Є. –Ш–Ј—Г—З–µ–љ –Њ—В —И–≤–µ–і—Б–Ї–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Э–Є–ї—Б –§–∞–±–Є–∞–љ –•–µ–ї–≥–µ —Д–Њ–љ –Ъ–Њ—Е –њ—А–µ–Ј 1904–≥. –У–µ–љ–µ—А–∞—В–Њ—А—К—В –љ–∞ —Д—А–∞–Ї—В–∞–ї–∞ –µ —А–∞–≤–љ–Њ—Б—В—А–∞–љ–µ–љ —В—А–Є—К–≥—К–ї–љ–Є–Ї, —Б—В—А–∞–љ–Є—В–µ –љ–∞ –Ї–Њ–є—В–Њ —Б–∞ —А–∞–≤–љ–Є –љ 1/3 –Њ—В –і—К–ї–ґ–Є–љ–∞—В–∞ –љ–∞ –≥–Њ–ї—П–Љ–∞—В–∞ –Њ—В—Б–µ—З–Ї–∞.
–Т—Б–µ–Ї–Є –ї–Є–љ–Є—П, –Ї–Њ—П—В–Њ –µ ___ —Б–µ –Ј–∞–Љ–µ–љ—П —Б 4 –ї–Є–љ–Є–Є, –≤—Б—П–Ї–∞ —Б –і—К–ї–ґ–Є–љ–∞ –Њ—В 1/3 –Њ—В –Њ—А–Є–≥–Є–љ–∞–ї–∞ _/\_. –° –≤—Б—П–Ї–∞ –Є—В–µ—А–∞—Ж–Є—П –і—К–ї–ґ–Є–љ–∞—В–∞ –љ–∞ –Ї—А–Є–≤–∞—В–∞ —Б–µ —Г–≤–µ–ї–Є—З–∞–≤–∞ —Б 1/3 –Њ—В –і—К–ї–ґ–Є–љ–∞—В–∞ –љ–∞ –Њ—В—Б–µ—З–Ї–∞—В–∞ –Њ—В –њ—А–µ–і–Є—И–љ–Є—П –µ—В–∞–њ.
|
–Ъ—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е (–≤–∞—А.1)
|
–Ь–∞–љ–і–µ–ї–±—А–Њ—В –Љ–љ–Њ–≥–Њ –µ –µ–Ї—Б–њ–µ—А–Є–Љ–µ–љ—В–Є—А–∞–ї —Б –Ї—А–Є–≤–Є—В–µ –љ–∞ –Ъ–Њ—Е, –Є –њ–Њ–ї—Г—З–Є–ї —В–∞–Ї–Є–≤–∞ —Д–Є–≥—Г—А–Є –Ї–∞—В–Њ –Ю—Б—В—А–Њ–≤–Є—В–µ –љ–∞ –Ъ–Њ—Е, –Ъ—А—К—Б—В–Њ–≤–µ—В–µ –љ–∞ –Ъ–Њ—Е, –°–љ–µ–ґ–Є–љ–Ї–Є—В–µ –љ–∞ –Ъ–Њ—Е –Є –і–∞–ґ–µ —В—А–Є–Љ–µ—А–љ–Є –Ї–Њ–љ—Б—В—А—Г–Ї—Ж–Є–Є –љ–∞ –Ї—А–Є–≤–∞—В–∞ –љ–∞ –Ъ–Њ—Е, –Є–Ј–њ–Њ–ї–Ј–≤–∞–є–Ї–Є —В–µ—В—А–∞–µ–і—К—А –Є –њ—А–Є–±–∞–≤—П–є–Ї–Є –њ–Њ-–Љ–∞–ї–Ї–Є –њ–Њ —А–∞–Ј–Љ–µ—А —В–µ—В—А–∞–µ–і—А–Є –Ї—К–Љ –≤—Б—П–Ї–∞ –Њ—В —Б—В–µ–љ–Є—В–µ –Љ—Г. –Ъ—А–Є–≤–∞—В–∞ –љ–∞ –Ъ–Њ—Е –Є–Љ–∞ —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В ln4/ln3 = 1.261859507. |
||||||||
–Ъ—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е (–≤–∞—А.2)-Cesaro 1905)
|
–Ъ—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е (–≤–∞—А.3)
|
||||||||||||||||||
–Э–∞–Ї—А–∞—П - —Б–∞–Љ–∞—В–∞ —Б–љ–µ–ґ–Є–љ–Ї–∞ –љ–∞ –Ъ–Њ—Е:
 |
|||||
| 1 | 2 | 3 | 4 | 5 | 6 |
–Р–Ї–Њ –љ–∞–њ—А–∞–≤–Є–Љ –±–µ–Ј–Ї—А–∞–µ–љ –±—А–Њ–є –Є—В–µ—А–∞—Ж–Є–Є, —Й–µ –њ–Њ–ї—Г—З–Є–Љ —Д—А–∞–Ї—В–∞–ї - —Б–љ–µ–ґ–Є–љ–Ї–∞ –љ–∞ –Ъ–Њ—Е —Б –±–µ–Ј–Ї—А–∞–є–љ–∞ –і—К–ї–ґ–Є–љ–∞. –Ю–Ї–∞–Ј–≤–∞ —Б–µ, –Њ–±–∞—З–µ, —З–µ —В–∞–Ј–Є –±–µ–Ј–Ї—А–∞–є–љ–∞ –Ї—А–Є–≤–∞ –Њ–≥—А–∞–ґ–і–∞ –Њ–≥—А–∞–љ–Є—З–µ–љ–∞ –њ–ї–Њ—Й.
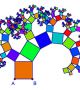
–Ф—А–∞–Ї–Њ–љ—К—В –Њ—В –Ї–љ–Є–≥–∞—В–∞ "–Ѓ—А—Б–Ї–Є –њ–∞—А–Ї" –љ–∞ –Ь–∞–є–Ї—К–ї –Ъ—А–∞–є—В—К–љ, (–•–∞—А—В–µ—А-–•–µ–є—В—Г–µ–є)
 –Э–∞–є-–Є–Ј–≤–µ—Б—В–љ–Є—П—В "–ї–Є—В–µ—А–∞—В—Г—А–µ–љ" —Д—А–∞–Ї—В–∞–ї. –Ю—В–Ї—А–Њ–≤–µ–љ–Є—П—В–∞ –љ–∞ –Ь–∞–ї–Ї—К–ї–Љ –≤ —В–∞–Ј–Є –Ї–љ–Є–≥–∞ –Љ–Є –і–∞–і–Њ—Е–∞ –њ—К—А–≤–Є—П —В–ї–∞—Б—К–Ї –і–∞ —Б–µ –Ј–∞–љ–Є–Љ–∞–≤–∞–Љ —Б —Д—А–∞–Ї—В–∞–ї–Є—В–µ. –Ь–Њ–ґ–µ –і–∞ —Б–µ –њ–Њ–ї—Г—З–Є –Љ–љ–Њ–≥–Њ –ї–µ—Б–љ–Њ –Ї–∞—В–Њ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ —Б–µ —Б–≥—К–≤–∞ –љ–∞ –і–≤–µ –ї–Є—Б—В —Е–∞—А—В–Є—П –Є —Б–µ —А–∞–Ј—В–≤–∞—А—П –і–Њ–Ї–∞—В–Њ —К–≥—К–ї–∞ —Б—В–∞–љ–µ 90–Њ.
–Э–∞–є-–Є–Ј–≤–µ—Б—В–љ–Є—П—В "–ї–Є—В–µ—А–∞—В—Г—А–µ–љ" —Д—А–∞–Ї—В–∞–ї. –Ю—В–Ї—А–Њ–≤–µ–љ–Є—П—В–∞ –љ–∞ –Ь–∞–ї–Ї—К–ї–Љ –≤ —В–∞–Ј–Є –Ї–љ–Є–≥–∞ –Љ–Є –і–∞–і–Њ—Е–∞ –њ—К—А–≤–Є—П —В–ї–∞—Б—К–Ї –і–∞ —Б–µ –Ј–∞–љ–Є–Љ–∞–≤–∞–Љ —Б —Д—А–∞–Ї—В–∞–ї–Є—В–µ. –Ь–Њ–ґ–µ –і–∞ —Б–µ –њ–Њ–ї—Г—З–Є –Љ–љ–Њ–≥–Њ –ї–µ—Б–љ–Њ –Ї–∞—В–Њ –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї–љ–Њ —Б–µ —Б–≥—К–≤–∞ –љ–∞ –і–≤–µ –ї–Є—Б—В —Е–∞—А—В–Є—П –Є —Б–µ —А–∞–Ј—В–≤–∞—А—П –і–Њ–Ї–∞—В–Њ —К–≥—К–ї–∞ —Б—В–∞–љ–µ 90–Њ.
–Ю—Й–µ –Ј–∞ "–і—А–∞–Ї–Њ–љ–∞" –љ–∞ –•–∞—А—В–µ—А-–•–µ–є—В—Г–µ–ї –Љ–Њ–ґ–µ –і–∞ —Б–µ –њ—А–Њ—З–µ—В–µ –≤ —В–µ–Љ–∞—В–∞ –Ј–∞ IFS
| –Э–∞—З—Г–њ–µ–љ–∞—В–∞ –і—А–∞–Ї–Њ–љ–Њ–≤–∞ –ї–Є–љ–Є—П –њ—А–Є–љ–∞–і–ї–µ–ґ–Є –µ –Ї—К–Љ –Ї–ї–∞—Б–∞ –љ–∞ —Б–∞–Љ–Њ–њ–Њ–і–Њ–±–љ–Є—В–µ —А–µ–Ї—Г—А—Б–Є–≤–љ–Њ –≥–µ–љ–µ—А–Є—А–∞–љ–Є –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є —Б—В—А—Г–Ї—В—Г—А–Є. –Ю—Б–љ–Њ–≤–∞—В–∞ –µ –њ—А–Њ—Б—В–Њ –њ—А–∞–≤ —К–≥—К–ї. –§–Є–≥—Г—А–∞—В–∞ —Б–µ –Є–Ј–≥—А–∞–ґ–і–∞ –Ј–∞ –≤—Б–µ–Ї–Є –µ—В–∞–њ –Њ—В —А–µ–Ї—Г—А—Б–Є–≤–љ–Є –Ј–∞–Љ–µ—Б—В–≤–∞–љ–Є—П –љ–∞ –≤—Б—П–Ї–∞ –µ–і–љ–∞ –Њ—В –Њ—В—Б–µ—З–Ї–Є—В–µ –љ–∞ —Д–Є–≥—Г—А–∞—В–∞ –Њ—В –њ—А–µ–і–Є—И–љ–Є—П –µ—В–∞–њ —Б –≥–µ–љ–µ—А–∞—В–Њ—А–∞ –≤—К–≤ —Д–Њ—А–Љ–∞—В–∞ –љ–∞ –њ—А–∞–≤ —К–≥—К–ї. |
|
||||||||||||||||||||||||
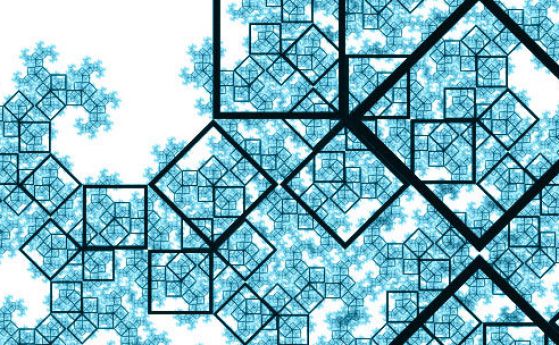
–†–µ—И–µ—В–Ї–∞—В–∞ –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є
–Ґ–Њ–Ј–Є –Ј–љ–∞–Љ–µ–љ–Є—В —Д—А–∞–Ї—В–∞–ї –µ –љ–∞—А–µ—З–µ–љ –љ–∞ –Є–Љ–µ—В–Њ –љ–∞ –Њ—В–Ї—А–Є–≤–∞—В–µ–ї—П —Б–Є - –њ–Њ–ї—Б–Ї–Є—П –Љ–∞—В–µ–Љ–∞—В–Є–Ї –Т–∞—Ж–ї–∞–≤ –°–µ—А–њ–Є–љ—Б–Ї–Є, –Ї–Њ–є—В–Њ –≥–Њ –µ –Њ–њ–Є—Б–∞–ї 1915–≥. –Ь–∞–љ–і–µ–ї–±—А–Њ—В –≥–Њ –њ—А–∞–≤–Є –Є–Ј–≤–µ—Б—В–µ–љ –њ–Њ–і –Є–Љ–µ—В–Њ "–≤—К–ґ–µ—В–Њ –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є" (Sierpinski gasket). –Я—А–Є–љ—Ж–Є–њ—К—В –љ–∞ –Є–Ј–≥—А–∞–ґ–і–∞–љ–µ—В–Њ –Љ—Г –µ –њ—А–Њ—Б—В: –≤—Б–µ–Ї–Є –µ–ї–µ–Љ–µ–љ—В —Б–µ –Ј–∞–Љ–µ–љ—П —Б n –±—А–Њ–є –њ–Њ–і–Њ–±–љ–Є –љ–∞ –љ–µ–≥–Њ –µ–ї–µ–Љ–µ–љ—В–Є. –°–њ–Њ—А–µ–і —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В—В–∞ —Б–Є –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В:
–µ–і–љ–Њ–Љ–µ—А–љ–Є–Є–ї–Є –≥—А–µ–±–µ–љ –љ–∞ –Ъ–∞–љ—В–Њ—А - –Њ–њ–Є—Б–∞–љ –Њ—В –У–µ–Њ—А–≥ –Ъ–∞–љ—В–Њ—А, –µ–і–Є–љ –Њ—В –Њ—Б–љ–Њ–≤–∞—В–µ–ї–Є—В–µ –љ–∞ —В–µ–Њ—А–Є—П—В–∞ –љ–∞ –Љ–љ–Њ–ґ–µ—Б—В–≤–∞—В–∞, –Њ—Й–µ –њ—А–µ–Ј 1883. –Ю–±—А–∞–Ј—Г–≤–∞ —Б–µ –љ–∞ –Њ—Б–љ–Њ–≤–∞—В–∞ –љ–∞ –њ—А–µ–Љ–∞—Е–≤–∞–љ–Є—П –љ–∞ —Б—А–µ–і–љ–∞—В–∞ —В—А–µ—В–Є–љ–∞ –љ–∞ –Њ—В—Б–µ—З–Ї–∞—В–∞ вАУ –њ–Њ–≤—В–Њ—А–µ–љ–Є–µ—В–Њ –љ–∞ –њ–Њ–і–Њ–±–љ–∞—В–∞ –Њ–њ–µ—А–∞—Ж–Є—П –і–Њ –±–µ–Ј–Ї—А–∞–є–љ–Њ—Б—В –≤–Њ–і–Є –і–Њ –Њ–±—А–∞–Ј—Г–≤–∞–љ–µ—В–Њ –љ–∞ —В.–љ. –Ї–∞–љ—В–Њ—А–Њ–≤—Б–Ї–Є –њ—А–∞—И–Є–љ–Ї–Є, —Б—Г–Љ–∞—В–∞ –Њ—В –і—К–ї–ґ–Є–љ–Є—В–µ –љ–∞ –Ї–Њ–Є—В–Њ –µ —А–∞–≤–љ–∞ –љ–∞ 0. –§—А–∞–Ї—В–∞–ї–љ–∞—В–∞ —А–∞–Ј–Љ–µ—А–љ–Њ—Б—В –Љ—Г –µ ln2/ln3 = 0.63 |
 |
–і–≤—Г–Љ–µ—А–љ–Є
–Э–∞–є-–Є–Ј–≤–µ—Б—В–љ–Є —Б–∞ —В—А–Є—К–≥—К–ї–љ–Є–Ї–∞ –Є —З–µ—В–Є—А–Є—К–≥—К–ї–љ–Є–Ї–∞ (–Ї–Є–ї–Є–Љ–∞) –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є (Sierpinski carpet).
–Ґ—А–Є—К–≥—К–ї–љ–Є–Ї –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є–Р—В—А–∞–Ї—В–Њ—А—К—В –µ: 3 –љ–Њ–≤–Є –њ–Њ–і–Њ–±–љ–Є —Д–Є–≥—Г—А–Є, —А–∞–Ј–њ–Њ–ї–Њ–ґ–µ–љ–Є —Б–Є–Љ–µ—В—А–Є—З–љ–Њ –љ–∞ 1/2 –Њ—В —Б—В—А–∞–љ–Є—В–µ. –†–∞–Ј–Љ–µ—А–љ–Њ—Б—В: ln3/ln2 = 1.585 |
|
||||||||||||
 
–І–µ—В–Є—А–Є—К–≥—К–ї–љ–Є–Ї (–Ї–Є–ї–Є–Љ) –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є(Sierpinski carpet)–Р—В—А–∞–Ї—В–Њ—А—К—В –µ: 8 –љ–Њ–≤–Є –њ–Њ–і–Њ–±–љ–Є —Д–Є–≥—Г—А–Є, –њ–Њ 3 –љ–∞ —Б—В—А–∞–љ–∞ –Є –њ–Њ –µ–і–Є–љ –љ–∞ –≤—К—А—Е–Њ–≤–µ—В–µ. –†–∞–Ј–Љ–µ—А–љ–Њ—Б—В: 3ln2/ln3 ~ 1.9 –Ф–Є–∞–≥–Њ–љ–∞–ї–Є—В–µ –љ–∞ "–Ї–Є–ї–Є–Љ–∞" –њ—А–µ–і—Б—В–∞–≤–ї—П–≤–∞—В –Љ–љ–Њ–ґ–µ—Б—В–≤–∞ –љ–∞ –Ъ–∞–љ—В–Њ—А |
|
||||||||||
–Ъ—А–Є–≤–∞ –љ–∞ —В—А–Є—К–≥—К–ї–љ–Є–Ї–∞ –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є (arrowhead curves)–Х–і–љ–∞ –Ї—А–Є–≤–∞, –Ї–Њ—П—В–Њ —Б–ї–µ–і –љ—П–Ї–Њ–ї–Ї–Њ –Є—В–µ—А–∞—Ж–Є–Є –Ї–ї–Њ–љ–Є –Ї—К–Љ —Д—А–∞–Ї—В–∞–ї–∞ –Ґ—А–Є—К–≥—К–ї–љ–Є–Ї –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є. |
|
||||||||||||||||
–Ґ—А–Є—К–≥—К–ї–љ–Є–Ї –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є —Б—К—Б –Ј–∞–≤—К—А—В–∞–љ–µ
|
–Р–Ї–Њ —Б–ї–µ–і —Б–ї–µ–і –≤—Б—П–Ї–∞ –Є—В–µ—А–∞—Ж–Є—П –≥–µ–љ–µ—А–∞—В–Њ—А—К—В —Б–µ –Ј–∞–≤—К—А—В–∞ —Б –Њ–њ—А–µ–і–µ–ї–µ–љ —К–≥—К–ї. –љ–∞–њ—А–Є–Љ–µ—А 1. –≤ –ї–µ–≤–Є—П –і–Њ–ї–µ–љ —К–≥—К–ї –њ–Њ –њ–Њ—Б–Њ–Ї–∞, –Њ–±—А–∞—В–љ–Њ –љ–∞ —З–∞—Б–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ |
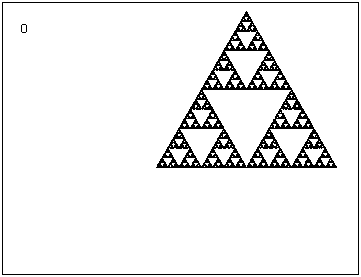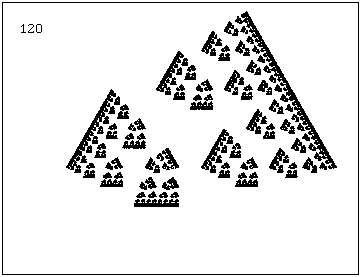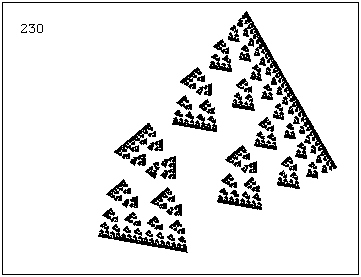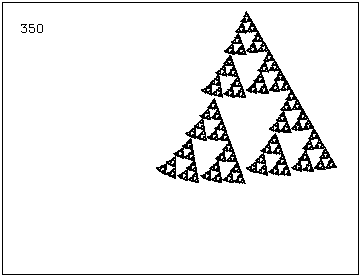 |
| 2. –≤¬†–ї–µ–≤–Є—П –і–Њ–ї–µ–љ —К–≥—К–ї, –Њ–±—А–∞—В–љ–Њ –љ–∞ —З–∞—Б–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞, –∞ –і–µ—Б–љ–Є—П –і–Њ–ї–µ–љ —К–≥—К–ї - –њ–Њ —З–∞—Б–Њ–≤–∞—В–∞ —Б—В—А–µ–ї–Ї–∞ –µ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ —Б –µ–і–Є–љ –Є —Б—К—Й —К–≥—К–ї | 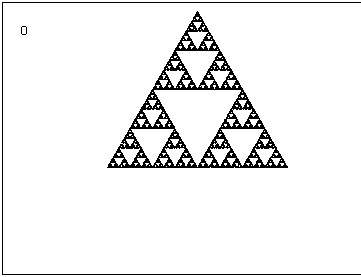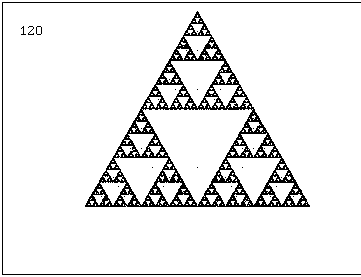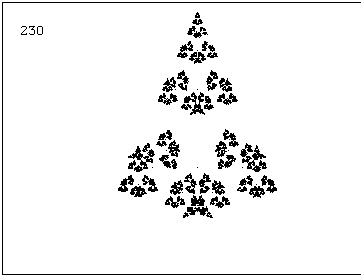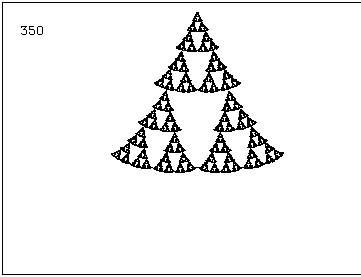 |
 |
–Ґ—А–Є–Є–Ј–Љ–µ—А–љ–Є–Э–∞–є-–Є–Ј–≤–µ—Б—В–µ–љ –≤ —В—А–Є–Є–Ј–Љ–µ—А–µ–љ –≤–Є–і –µ "–Ї–Є–ї–Є–Љ–∞" –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є, –Є–Ј–≤–µ—Б—В–µ–љ –Њ—Й–µ –Ї–∞—В–Њ " –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є-–Ь–µ–љ–≥–µ—А (–Ъ–∞—А–ї –Ь–µ–љ–≥–µ—А 1902 - 1985 -–∞–Љ–µ—А. –Љ–∞—В–µ–Љ–∞—В–Є–Ї). –Р—В—А–∞–Ї—В–Њ—А—К—В –µ: 20 –љ–Њ–≤–Є –њ–Њ–і–Њ–±–љ–Є —В–µ–ї–∞, —Ж–µ–љ—В—А–Є—А–∞–љ–Є –њ–Њ 3 –Ї—К–Љ –≤—Б–µ–Ї–Є —А—К–±. –†–∞–Ј–Љ–µ—А–љ–Њ—Б—В: ln20/ln3 ~ 2.7. –Э–∞–њ–Њ–і–Њ–±—П–≤–∞ –Ї–Њ—Б—В–љ–∞ —Б—В—А—Г–Ї—В—Г—А–∞. –°–ї–µ–і –±–µ–Ј–±—А–Њ–є –Є—В–µ—А–∞—Ж–Є–Є —Й–µ —Б–µ –њ—А–µ–≤—К—А–љ–µ –≤ "–њ—А–∞—Е" –љ–∞ –Ъ–∞–љ—В–Њ—А, –Ї–∞–Ї—В–Њ –≤–њ—А–Њ—З–µ–Љ –Є –љ–∞—И–Є—В–µ –Ї–Њ—Б—В–Є. |
| –Є –Њ—Й–µ –µ–і–Є–љ –µ–і–Є–љ –≤–∞—А–Є–∞–љ—В –љ–∞ —В–µ—В—А–∞–µ–і—К—А –њ–Њ –°–µ—А–њ–Є–љ—Б–Ї–Є: |
|
||||||||||||
–Р–ї–≥–µ–±—А–Є—З–љ–Є —Д—А–∞–Ї—В–∞–ї–Є
–Ґ–Њ–≤–∞ –µ –і—А—Г–≥–∞—В–∞ –Њ—Б–љ–Њ–≤–љ–∞ –≥—А—Г–њ–∞ —Д—А–∞–Ї—В–∞–ї–Є. –Э–∞—А–Є—З–∞—В —Б–µ –∞–ї–≥–µ–±—А–Є—З–љ–Є, –Ј–∞—Й–Њ—В–Њ —В–µ —Б–∞ –Є–Ј–≥—А–∞–і–µ–љ–Є –љ–∞ –±–∞–Ј–∞—В–∞ –љ–∞ –∞–ї–≥–µ–±—А–Є—З–љ–Є —Д–Њ—А–Љ—Г–ї–Є. –Ч–∞ –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є –љ–µ —Б–∞ –љ—Г–ґ–љ–Є —Д–Њ—А–Љ—Г–ї–Є –Є–ї–Є —Г—А–∞–≤–љ–µ–љ–Є—П, –Ј–∞—В–Њ–≤–∞ –≤—Б–µ–Ї–Є –Љ–Њ–ґ–µ –і–∞ –љ–∞—З–µ—А—В–∞–µ —А–µ—И–µ—В–Ї–∞—В–∞ –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є –і–Њ 3 –Є–ї–Є 4 –Є—В–µ—А–∞—Ж–Є—П –±–µ–Ј –љ–Є–Ї–∞–Ї–≤–Є –Ј–∞—В—А—Г–і–љ–µ–љ–Є—П, –љ–Њ –і–∞ —Б–µ –љ–∞–њ—А–∞–≤–Є —В–Њ–≤–∞, –љ–∞–њ—А–Є–Љ–µ—А, —Б –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ—В–Њ –љ–∞ –Ц—Г–ї–Є–∞ –µ —В–Њ–ї–Ї–Њ–≤–∞ –љ–µ–≤—К–Ј–Љ–Њ–ґ–љ–Њ –Ї–Њ–ї–Ї–Њ—В–Њ –і–∞ —Б–µ –Є–Ј–Љ–µ—А–Є –і—К–ї–ґ–Є–љ–∞—В–∞ –љ–∞ –±—А–µ–≥–Њ–≤–∞—В–∞ –ї–Є–љ–Є—П –љ–∞ –Р–љ–≥–ї–Є—П.
–Р–ї–≥–µ–±—А–Є—З–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є –Є–Ј–≥–ї–µ–ґ–і–∞—В –±–µ–Ј–Ї—А–∞–є–љ–Њ —Б–ї–Њ–ґ–љ–Є –≤ —Б—А–∞–≤–љ–µ–љ–Є–µ —Б –≥–µ–Њ–Љ–µ—В—А–Є—З–љ–Є—В–µ, –љ–Њ –Љ–Њ–≥–∞—В –і–∞ –±—К–і–∞—В –≥–µ–љ–µ—А–Є—А–∞–љ–Є —Б –Љ–љ–Њ–≥–Њ –њ—А–Њ—Б—В–∞ —Д–Њ—А–Љ—Г–ї–∞. –Ш–Љ–∞ –љ—П–Ї–Њ–ї–Ї–Њ –љ–∞—З–Є–љ–∞ –Ј–∞ –њ–Њ–ї—Г—З–∞–≤–∞–љ–µ –љ–∞ –∞–ї–≥–µ–±—А–Є—З–љ–Є —Д—А–∞–Ї—В–∞–ї–Є.
–Я—К—А–≤–Є—П—В –Љ–µ—В–Њ–і –µ –љ–∞ –±–∞–Ј–∞—В–∞ –љ–∞ –Љ–љ–Њ–≥–Њ–Ї—А–∞—В–љ–Њ –Є—В–µ—А–∞—Ж–Є–Њ–љ–љ–Њ –њ—А–µ—Б–Љ—П—В–∞–љ–µ –љ–∞ —Д—Г–љ–Ї—Ж–Є—П—В–∞:
zn+1= f(zn), –Ї—К–і–µ—В–Њ z –µ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ —З–Є—Б–ї–Њ, –∞ f –µ –љ—П–Ї–∞–Ї–≤–∞ —Д—Г–љ–Ї—Ж–Є—П.
–Ш–Ј—З–Є—Б–ї—П–≤–∞–љ–µ—В–Њ –љ–∞ —В–∞–Ј–Є —Д—Г–љ–Ї—Ж–Є—П –њ—А–Њ–і—К–ї–ґ–∞–≤–∞ –і–Њ–Ї–∞—В–Њ –љ–µ –±—К–і–∞—В –Є–Ј–њ—К–ї–љ–µ–љ–Є –Њ–њ—А–µ–і–µ–ї–µ–љ–Є —Г—Б–ї–Њ–≤–Є—П –Є –Ї–Њ–≥–∞—В–Њ —В–Њ–≤–∞ —Г—Б–ї–Њ–≤–Є–µ —Б–µ –Є–Ј–њ—К–ї–љ–Є, –љ–∞ –µ–Ї—А–∞–љ–∞ —Б–µ –њ–Њ—П–≤—П–≤–∞ —В–Њ—З–Ї–∞. –§—Г–љ–Ї—Ж–Є—П—В–∞ –Љ–Њ–ґ–µ –і–∞ –Є–Љ–∞ —А–∞–Ј–ї–Є—З–љ–Њ –њ–Њ–≤–µ–і–µ–љ–Є–µ:–Ј–∞ —А–∞–Ј–ї–Є—З–љ–Є —В–Њ—З–Ї–Є –≤ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–∞—В–∞ —А–∞–≤–љ–Є–љ–∞.
–Я–Њ—Б—В—А–Њ—П–≤–∞–љ–µ—В–Њ –љ–∞ –∞–ї–≥–µ–±—А–Є—З–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є –µ —Б–≤—К—А–Ј–∞–љ–Њ —Б –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Є—В–µ —З–Є—Б–ї–∞, –Ј–∞ —В—П—Е –Є –њ–Њ-–Є–Ј–≤–µ—Б—В–љ–Є—В–µ —Д—А–∞–Ї—В–∞–ї–Є —Й–µ –њ—А–Њ—З–µ—В–µ—В–µ –≤ –Њ—В–і–µ–ї–љ–∞ —В–µ–Љ–∞.
–°—В–Њ—Е–∞—Б—В–Є—З–љ–Є (—Б–ї—Г—З–∞–є–љ–Є) —Д—А–∞–Ї—В–∞–ї–Є
–Я—А–Є—А–Њ–і–љ–Є—В–µ —П–≤–ї–µ–љ–Є—П –љ–µ –њ—А–Њ—В–Є—З–∞—В –≤ —Б—В–µ—А–Є–ї–љ–∞, –Є–Ј–Њ–ї–Є—А–∞–љ–∞ —Б—А–µ–і–∞, –∞ –≤ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Є —Г—Б–ї–Њ–≤–Є—П, —Б—К—З–µ—В–∞–љ–Є–µ –Њ—В –Љ–љ–Њ–ґ–µ—Б—В–≤–Њ –њ—А–µ–њ–ї–µ—В–µ–љ–Є —Б–ї—Г—З–∞–є–љ–Є –≤–ї–Є—П–љ–Є—П –Њ—В¬†–≤—К–љ—И–љ–Є —Д–∞–Ї—В–Њ—А–Є, –Ј–∞—В–Њ–≤–∞ –≤ –њ—А–Є—А–Њ–і–∞—В–∞ —Д—А–∞–Ї—В–∞–ї–Є—В–µ –љ–µ –Є–Ј–≥–ї–µ–ґ–і–∞—В —В–∞–Ї–∞ –Є–Ј—З–Є—Б—В–µ–љ–Є¬†–Ї–∞–Ї—В–Њ –Є–ї—О—Б—В—А–∞—Ж–Є–Є—В–µ –і–Њ—Б–µ–≥–∞. –Ч–∞ –Љ–Њ–і–µ–ї–Є—А–∞–љ–µ—В–Њ –Є–Љ¬†—Б–µ –Є–Ј–њ–Њ–ї–Ј–≤–∞—В —Б—В–Њ—Е–∞—Б—В–Є—З–љ–Є (—Б–ї—Г—З–∞–є–љ–Є) —Д—А–∞–Ї—В–∞–ї–Є.
–°—В–Њ—Е–∞—Б—В–Є—З–µ–љ —Д—А–∞–Ї—В–∞–ї –µ —В—А–∞–µ–Ї—В–Њ—А–Є—П—В–∞ –љ–∞ –С—А–∞—Г–љ–Њ–≤–Њ –і–≤–Є–ґ–µ–љ–Є–µ. –Ґ–∞–Ї–Є–≤–∞ —Д—А–∞–Ї—В–∞–ї–Є —Б–∞ —А–∞–љ–і–Њ–Љ–Є–Ј–Є—А–∞–љ–Є, —В.–µ. –њ—А–Є¬†–њ–Њ—Б—В—А–Њ—П–≤–∞–љ–µ—В–Њ –Є–Љ, –Ј–∞ –≤—Б—П–Ї–∞ —А–µ–Ї—Г—А—Б–Є–≤–љ–∞ —Б—В—К–њ–Ї–∞ –і–∞ —Б–µ¬†–≤—К–≤–µ–ґ–і–∞—В —Б–ї—Г—З–∞–є–љ–Є –≤–µ–ї–Є—З–Є–љ–Є.
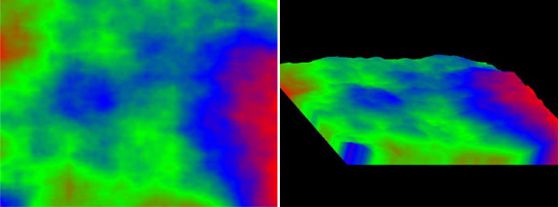
–§—А–∞–Ї—В–∞–ї—К—В "–њ–ї–∞–Ј–Љ–∞" –Њ—В –Ї–Њ–Љ–њ—О—В—К—А–љ–∞—В–∞ –≥—А–∞—Д–Є–Ї–∞ –µ —В–Є–њ–Є—З–µ–љ –њ—А–µ–і—Б—В–∞–≤–Є—В–µ–ї –љ–∞ —Б—В–Њ—Е–∞—Б—В–Є—З–µ–љ —Д—А–∞–Ї—В–∞–ї.
–Ч–∞ –њ–Њ—Б—В—А–Њ—П–≤–∞–љ–µ—В–Њ –Љ—Г –і–∞ –≤–Ј–µ–Љ–µ–Љ –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Є–Ї –Є –Ј–∞ –≤—Б–µ–Ї–Є –љ–µ–≥–Њ–≤ —К–≥—К–ї –і–∞ –Њ–њ—А–µ–і–µ–ї–Є–Љ —Ж–≤—П—В. –Э–∞–Љ–Є—А–∞–Љ–µ —Ж–µ–љ—В—А–∞–ї–љ–∞—В–∞ —В–Њ—З–Ї–∞ –љ–∞ –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Є–Ї–∞ –Є —П –Њ—Ж–≤–µ—В—П–≤–∞–Љ–µ –≤ —Ж–≤—П—В —А–∞–≤–µ–љ –љ–∞ —Б—А–µ–і–љ–Њ –∞—А–Є—В–Љ–µ—В–Є—З–љ–Њ—В–Њ –Њ—В —Ж–≤–µ—В–Њ–≤–µ—В–µ –њ–Њ —К–≥–ї–Є—В–µ –љ–∞ –њ—А–∞–≤–Њ—К–≥—К–ї–љ–Є–Ї–∞ –њ–ї—О—Б –љ—П–Ї–∞–Ї–≤–Њ —Б–ї—Г—З–∞–є–љ–Њ —З–Є—Б–ї–Њ. –Ъ–Њ–ї–Ї–Њ—В–Њ –µ –њ–Њ-–≥–Њ–ї—П–Љ–Њ —Б–ї—Г—З–∞–є–љ–Њ—В–Њ —З–Є—Б–ї–Њ - —В–Њ–ї–Ї–Њ–≤–∞ –њ–Њ-"–љ–∞–Ї—К—Б–∞–љ–∞" —Й–µ –±—К–і–µ –Ї–∞—А—В–Є–љ–Ї–∞—В–∞. –Ш —Б–µ–≥–∞, –∞–Ї–Њ —А–µ—З–µ–Љ, —З–µ —Ж–≤–µ—В—К—В –Њ–њ—А–µ–і–µ–ї—П –љ–∞–і–Љ–Њ—А—Б–Ї–∞ –≤–Є—Б–Њ—З–Є–љ–∞ - —Й–µ –њ–Њ–ї—Г—З–Є–Љ –≤–Љ–µ—Б—В–Њ –њ–ї–∞–Ј–Љ–∞ - –њ–ї–∞–љ–Є–љ—Б–Ї–Є –Љ–∞—Б–Є–≤. –Ш–Љ–µ–љ–љ–Њ –љ–∞ —В–Њ–Ј–Є –њ—А–Є–љ—Ж–Є–њ —Б–µ –Љ–Њ–і–µ–ї–Є—А–∞ —А–µ–ї–µ—Д –Њ—В¬†–њ–Њ–≤–µ—З–µ—В–Њ –њ—А–Њ–≥—А–∞–Љ–Є.
–Ю—Б–љ–Њ–≤–љ–Є –њ–Њ–љ—П—В–Є—П –Є –ї–µ–Ї—Б–Є–Ї–∞
- –§—А–∞–Ї—В–∞–ї–Є
- –У–µ–Њ–Љ–µ—В—А–Є—З–љ–Є —Д—А–∞–Ї—В–∞–ї–Є
- –Є—В–µ—А–∞—Ж–Є–Є
- –Њ—Б–љ–Њ–≤–∞ (–≥–µ–љ–µ—А–∞—В–Њ—А)
- —Б–љ–µ–ґ–Є–љ–Ї–∞ –љ–∞ –Ъ–Њ—Е
- –Ї—А–Є–≤–∞ –љ–∞ –Ъ–Њ—Е
- –Ї—А–Є–≤–∞ –љ–∞ Cesaro
- –і—А–∞–Ї–Њ–љ –љ–∞ –•–∞—А—В–µ—А-–•–µ–є—В—Г–µ–ї
- –≥—А–µ–±–µ–љ –љ–∞ –Ъ–∞–љ—В–Њ—А
- —В—А–Є—К–≥—К–ї–љ–Є–Ї –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є
- —З–µ—В–Є—А–Є—К–≥—К–ї–љ–Є–Ї (–Ї–Є–ї–Є–Љ) –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є
- –Ї—А–Є–≤–∞ –љ–∞ —В—А–Є—К–≥—К–ї–љ–Є–Ї–∞ –љ–∞ –°–µ—А–њ–Є–љ—Б–Ї–Є
- –µ–і–љ–Њ–Љ–µ—А–љ–Є
- –і–≤—Г–Љ–µ—А–љ–Є
- —В—А–Є–Є–Ј–Љ–µ—А–љ–Є
- –Р–ї–≥–µ–±—А–Є—З–љ–Є —Д—А–∞–Ї—В–∞–ї–Є
- –°—В–Њ—Е–∞—Б—В–Є—З–љ–Є (—Б–ї—Г—З–∞–є–љ–Є) —Д—А–∞–Ї—В–∞–ї–Є
- —А–∞–љ–і–Њ–Љ–Є–Ј–∞—Ж–Є—П
- —Д—А–∞–Ї—В–∞–ї—К—В "–њ–ї–∞–Ј–Љ–∞"
- –Э–Є–ї—Б –§–∞–±–Є–∞–љ –•–µ–ї–≥–µ —Д–Њ–љ –Ъ–Њ—Е
- –Т–∞—Ж–ї–∞–≤ –§—А–∞–љ—Ж–Є—Б–Ї –°–µ—А–њ–Є–љ—Б–Ї–Є
- –С–µ–љ–Њ–∞ –Ь–∞–љ–і–µ–ї–±—А–Њ—В
–Ш–Ј—В–Њ—З–љ–Є—Ж–Є:
–§—А–∞–Ї—В–∞–ї—М–љ–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П –њ—А–Є—А–Њ–і—Л, –Ь–∞–љ–і–µ–ї—М–±—А–Њ—В –С.
Fractal Geometry, Yale University, Michael Frame, Benoit Mandelbrot (1924-2010), and Nial Neger
–Т–≤–µ–і–µ–љ–Є–µ –≤–Њ —Д—А–∞–Ї—В–∞–ї—Л, –®–∞–±–∞—А—И–Є–љ –Р.–Р.
–У–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Є–µ —Д—А–∞–Ї—В–∞–ї—Л, –Х–≤–≥–µ–љ–Є–є –Х–њ–Є—Д–∞–љ–Њ–≤




























–Ъ–Њ–Љ–µ–љ—В–∞—А–Є
–Ь–Њ–ї—П, —А–µ–≥–Є—Б—В—А–Є—А–∞–є—В–µ —Б–µ –Њ—В T–£–Ъ!
–Р–Ї–Њ –≤–µ—З–µ –Є–Љ–∞—В–µ —А–µ–≥–Є—Б—В—А–∞—Ж–Є—П, –љ–∞—В–Є—Б–љ–µ—В–µ –Ґ–£–Ъ!
–Э—П–Љ–∞ –Ї–Њ–Љ–µ–љ—В–∞—А–Є –Ї—К–Љ —В–∞–Ј–Є –љ–Њ–≤–Є–љ–∞ !
–Я–Њ—Б–ї–µ–і–љ–Є –Ї–Њ–Љ–µ–љ—В–∞—А–Є
4I4ATA
–Э–Њ–≤, —Б–Ї—А–Є—В –і–Њ—Б–µ–≥–∞ –≤—Е–Њ–і –≤ –њ–Є—А–∞–Љ–Є–і–∞—В–∞ –љ–∞ –Ь–Є–Ї–µ—А–Є–љ –µ –Њ—В–Ї—А–Є—В –њ–Њ –∞–љ–Њ–Љ–∞–ї–Є–Є –њ—А–Є —Б–Ї–∞–љ–Є—А–∞–љ–µ
YKoshev
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Johnny B Goode
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews
Gunteer
–Я—А–µ—Б—В–Є–ґ–љ–∞ –љ–∞–≥—А–∞–і–∞ –Њ—В –С–Р–Э —Б–њ–µ—З–µ–ї–Є –≥–ї–∞–≤–љ–Є—П—В —А–µ–і–∞–Ї—В–Њ—А –љ–∞ –Э–∞—Г–Ї–∞OFFNews