

–ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł —Ā–į –ĺ—ā–ļ—Ä–ł–Ľ–ł, —á–Ķ —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–ł –ī–į —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į–ľ–Ķ –ī—ä—Ä–≤–Ķ—ā–į—ā–į –≤ –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–į —Ā –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ł–Ĺ—Ü–ł–Ņ, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ —Ā—ā–Ķ–Ņ–Ķ–Ĺ –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ. –Ę–į–∑–ł –∑–į–ļ–ĺ–Ĺ–ĺ–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā, –ĺ—ā–ļ—Ä–ł—ā–į –≤ –ł—Ā—ā–ł–Ĺ—Ā–ļ–ł—ā–Ķ –ī—ä—Ä–≤–Ķ—ā–į, —Ā–Ķ –Ņ–ĺ—Ź–≤—Ź–≤–į –≤ —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ö—É–ī–ĺ–∂–Ķ—Ā—ā–≤–Ķ–Ĺ–ł —Ā—ā–ł–Ľ–ĺ–≤–Ķ –ł –ļ—É–Ľ—ā—É—Ä–ł, –ļ–ĺ–Ķ—ā–ĺ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–≤–į –ī–ĺ—Ä–ł –į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ł—ā–Ķ –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –ī–į –Ī—ä–ī–į—ā —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į–Ķ–ľ–ł.
–Ē–ĺ–ļ–į—ā–ĺ –ļ—Ä–į—Ā–ĺ—ā–į—ā–į –Ĺ–į –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –Ķ —Ā—É–Ī–Ķ–ļ—ā–ł–≤–Ĺ–į, —Ā–Ņ–ĺ—Ā–ĺ–Ī–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–ł –ī–į —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į–ľ–Ķ –ī—ä—Ä–≤–Ķ—ā–į—ā–į –≤ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ –ľ–ĺ–∂–Ķ –ī–į –Ķ —Ā–≤—ä—Ä–∑–į–Ĺ–į —Ā –ĺ–Ī–Ķ–ļ—ā–ł–≤–Ĺ–į - –ł —Ā—Ä–į–≤–Ĺ–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ņ—Ä–ĺ—Ā—ā–į - –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į, —Ā–Ņ–ĺ—Ä–Ķ–ī –Ĺ–ĺ–≤–ĺ –Ņ—Ä–ĺ—É—á–≤–į–Ĺ–Ķ.
–ü—Ä–ĺ—É—á–≤–į–Ĺ–Ķ—ā–ĺ, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–ĺ –ĺ—ā –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł –ĺ—ā –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –ú–ł—á–ł–≥–į–Ĺ –ł –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –Ě—é –ú–Ķ–ļ—Ā–ł–ļ–ĺ, –ł–∑—Ā–Ľ–Ķ–ī–≤–į –ļ–į–ļ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–į—ā–į –ī–Ķ–Ī–Ķ–Ľ–ł–Ĺ–į –Ĺ–į —Ä–į–∑–ļ–Ľ–ĺ–Ĺ—Ź–≤–į—Č–ł—ā–Ķ —Ā–Ķ –ļ–Ľ–ĺ–Ĺ–ł –Ĺ–į –ī—ä—Ä–≤–ĺ—ā–ĺ –≤–Ľ–ł—Ź–Ķ –≤—ä—Ä—Ö—É –Ĺ–Ķ–≥–ĺ–≤–ł—Ź –ĺ–Ī–Ľ–ł–ļ –Ĺ–į –ī—ä—Ä–≤–ĺ.
–í—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ —Ö—É–ī–ĺ–∂–Ĺ–ł—Ü–ł—ā–Ķ, –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł, —Ā–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ľ–ł —ā–į–∑–ł –ļ–ĺ–Ĺ—Ü–Ķ–Ņ—Ü–ł—Ź –≤ –Ņ—Ä–ĺ–ī—ä–Ľ–∂–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–Ķ–ļ–ĺ–≤–Ķ, –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —Ā–į –≤–ļ–Ľ—é—á–ł–Ľ–ł –Ņ–ĺ-–Ĺ–ĺ–≤ –ļ–Ľ–ĺ–Ĺ –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į –≤ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ķ—ā–ĺ, –∑–į –ī–į —Ä–į–∑–ļ—Ä–ł—Ź—ā –Ņ–ĺ-–ī—ä–Ľ–Ī–ĺ–ļ–ł –Ņ—Ä–ĺ–∑—Ä–Ķ–Ĺ–ł—Ź.
"–ė–ľ–į –Ĺ—Ź–ļ–ĺ–ł —Ö–į—Ä–į–ļ—ā–Ķ—Ä–ł—Ā—ā–ł–ļ–ł –Ĺ–į –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ, –ļ–ĺ–ł—ā–ĺ —Ā—Ź–ļ–į—ą —Ā–į –Ķ—Ā—ā–Ķ—ā–ł—á–Ķ—Ā–ļ–ł –ł–Ľ–ł —Ā—É–Ī–Ķ–ļ—ā–ł–≤–Ĺ–ł, –Ĺ–ĺ –Ĺ–ł–Ķ –ľ–ĺ–∂–Ķ–ľ –ī–į –ł–∑–Ņ–ĺ–Ľ–∑–≤–į–ľ–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į, –∑–į –ī–į –≥–ł –ĺ–Ņ–ł—ą–Ķ–ľ", –∑–į—Ź–≤—Ź–≤–į –Ē–∂–ł–Ĺ–ī–∂–ł –ď–į–ĺ (Jingyi Gao), –≤–ĺ–ī–Ķ—Č –į–≤—ā–ĺ—Ä –Ĺ–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ. "–°–ľ—Ź—ā–į–ľ, —á–Ķ —ā–ĺ–≤–į –Ķ —Ā—ā—Ä–į—Ö–ĺ—ā–Ĺ–ĺ."
–ď–į–ĺ –ł–∑–≤—ä—Ä—ą–≤–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ –ļ–į—ā–ĺ –Ī–į–ļ–į–Ľ–į–≤—ä—Ä –≤ –ļ–į—ā–Ķ–ī—Ä–į—ā–į –Ņ–ĺ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į –Ĺ–į –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –ú–ĺ–Ĺ–į–ļ–ĺ, —Ä–į–Ī–ĺ—ā–Ķ–Ļ–ļ–ł —Ā –ú–ł—á—ä–Ľ –Ě—é–Ī—ä—Ä–ł (Mitchell Newberry), –ļ–ĺ–Ļ—ā–ĺ —Ā–Ķ–≥–į –Ķ –ī–ĺ—Ü–Ķ–Ĺ—ā –≤ –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –ú–ĺ–Ĺ–į–ļ–ĺ –ł —Ā—ä—ā—Ä—É–ī–Ĺ–ł–ļ –Ĺ–į –¶–Ķ–Ĺ—ā—ä—Ä–į –∑–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ –Ĺ–į —Ā–Ľ–ĺ–∂–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ł –Ĺ–į –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –ú–ĺ–Ĺ–į–ļ–ĺ. –°–Ķ–≥–į –ď–į–ĺ –Ķ –ī–ĺ–ļ—ā–ĺ—Ä–į–Ĺ—ā –≤ –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –£–ł—Ā–ļ–ĺ–Ĺ—Ā–ł–Ĺ.
–ü–ĺ-—Ā–Ņ–Ķ—Ü–ł–į–Ľ–Ĺ–ĺ –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —Ä–į–∑–ļ—Ä–ł–≤–į—ā –Ķ–ī–Ĺ–į –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ–Ĺ–į –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, —Ā–≤—ä—Ä–∑–į–Ĺ–į —Ā—ä—Ā —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—ā–į –ł –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ł—ā–Ķ –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –Ĺ–į –ī—ä—Ä–≤–ĺ—ā–ĺ, –ļ–ĺ—Ź—ā–ĺ —Ö—É–ī–ĺ–∂–Ĺ–ł—Ü–ł—ā–Ķ –∑–į–Ņ–į–∑–≤–į—ā –ł —Ā –ļ–ĺ—Ź—ā–ĺ —Ā–ł —Ā–Ľ—É–∂–į—ā, –∑–į –ī–į –Ņ–ĺ–≤–Ľ–ł—Ź—Ź—ā –ī–į–Ľ–ł –ł –ļ–į–ļ –∑—Ä–ł—ā–Ķ–Ľ–ł—ā–Ķ –≤—ä–∑–Ņ—Ä–ł–Ķ–ľ–į—ā –ī—ä—Ä–≤–ĺ—ā–ĺ.
"–Ę—É–ļ —Ā—ā–ł–≥–Ĺ–į—Ö–ľ–Ķ –ī–ĺ –Ĺ–Ķ—Č–ĺ —É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ĺ–ĺ, –ļ–ĺ–Ķ—ā–ĺ –≤ –ł–∑–≤–Ķ—Ā—ā–Ķ–Ĺ —Ā–ľ–ł—Ā—ä–Ľ —Ā–Ķ –ĺ—ā–Ĺ–į—Ā—Ź –∑–į –≤—Ā–ł—á–ļ–ł –ī—ä—Ä–≤–Ķ—ā–į –≤ –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ –ł –≤ –Ņ—Ä–ł—Ä–ĺ–ī–į—ā–į", –ĺ—ā–Ī–Ķ–Ľ—Ź–∑–≤–į –Ě—é–Ī—ä—Ä–ł, —Ā—ā–į—Ä—ą–ł –į–≤—ā–ĺ—Ä –Ĺ–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ. "–Ę–ĺ –Ķ –≤ –ĺ—Ā–Ĺ–ĺ–≤–į—ā–į –Ĺ–į –ľ–Ĺ–ĺ–≥–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ĺ–į –ī—ä—Ä–≤–Ķ—ā–į, –ī–ĺ—Ä–ł –ł –ī–į —Ā–į –≤ —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ā—ā–ł–Ľ–ĺ–≤–Ķ –ł —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ļ—É–Ľ—ā—É—Ä–ł –ł–Ľ–ł –≤–Ķ–ļ–ĺ–≤–Ķ."
–†–į–Ī–ĺ—ā–į—ā–į –Ķ –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ–į –≤ —Ā–Ņ–ł—Ā–į–Ĺ–ł–Ķ PNAS Nexus.
–Ę—Ä—Ź–Ī–≤–į –ī–į –Ĺ–į–ľ–Ķ—Ā–ł–ľ¬†—Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ
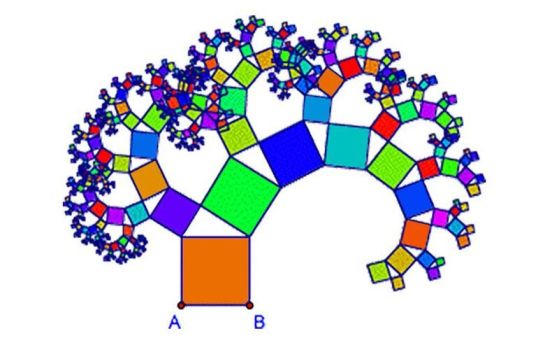
–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –ļ–ĺ—Ź—ā–ĺ –ī–≤–į–ľ–į—ā–į –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā, –∑–į –ī–į –Ņ–ĺ–ī—Ö–ĺ–ī—Ź—ā –ļ—ä–ľ —Ā–≤–ĺ—Ź –≤—ä–Ņ—Ä–ĺ—Ā –∑–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł–ł—ā–Ķ, —Ā–Ķ –ļ–ĺ—Ä–Ķ–Ĺ–ł –≤—ä–≤ —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ. –ě—ā –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—á–Ĺ–į –≥–Ľ–Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į —Ą—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ —Ā–į —Ā—ā—Ä—É–ļ—ā—É—Ä–ł, –ļ–ĺ–ł—ā–ĺ –Ņ–ĺ–≤—ā–į—Ä—Ź—ā –Ķ–ī–Ĺ–ł –ł —Ā—ä—Č–ł –ľ–ĺ—ā–ł–≤–ł –≤ —Ä–į–∑–Ľ–ł—á–Ĺ–ł –ľ–į—Č–į–Ī–ł.
–§—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ —Ā–į —Ā–Ņ–ĺ–ľ–Ķ–Ĺ–į—ā–ł –≤ —Ā–Ņ–Ķ—á–Ķ–Ľ–ł–Ľ–ł—Ź –ě—Ā–ļ–į—Ä —Ö–ł—ā "Let it Go" –ĺ—ā —Ą–ł–Ľ–ľ–į –Ĺ–į –Ē–ł—Ā–Ĺ–ł " Frozen", –Ņ–ĺ—Ä–į–ī–ł –ļ–ĺ–Ķ—ā–ĺ –Ķ —ā—Ä—É–ī–Ĺ–ĺ –ī–į —Ā–Ķ —ā–≤—ä—Ä–ī–ł, —á–Ķ –ł–ľ–į –Ņ–ĺ-–Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ķ–Ĺ —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ł–ľ–Ķ—Ä –ĺ—ā —Ā–į–ľ–ĺ–Ņ–ĺ–≤—ā–į—Ä—Ź—Č–ł—ā–Ķ —Ā–Ķ –ļ—Ä–ł—Ā—ā–į–Ľ–Ĺ–ł –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł–ł –Ĺ–į —Ā–Ĺ–Ķ–∂–ł–Ĺ–ļ–ł—ā–Ķ. –Ě–ĺ –Ī–ł–ĺ–Ľ–ĺ–≥–ł—Ź—ā–į —Ā—ä—Č–ĺ –Ķ –Ņ—ä–Ľ–Ĺ–į —Ā –≤–į–∂–Ĺ–ł —Ą—Ä–į–ļ—ā–į–Ľ–ł, –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ä–į–∑–ļ–Ľ–ĺ–Ĺ—Ź–≤–į—Č–ł—ā–Ķ —Ā–Ķ —Ā—ā—Ä—É–ļ—ā—É—Ä–ł –Ĺ–į –Ī–Ķ–Ľ–ł—ā–Ķ –ī—Ä–ĺ–Ī–ĺ–≤–Ķ, –ļ—Ä—ä–≤–ĺ–Ĺ–ĺ—Ā–Ĺ–ł—ā–Ķ —Ā—ä–ī–ĺ–≤–Ķ –ł, —Ä–į–∑–Ī–ł—Ä–į —Ā–Ķ, –ī—ä—Ä–≤–Ķ—ā–į—ā–į.
 –Ę–Ķ–∑–ł –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ĺ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–Ĺ–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ļ–į–∑–≤–į—ā –ļ–į–ļ —Ā –Ņ—Ä–ĺ–ľ—Ź–Ĺ–į—ā–į –Ĺ–į –ľ–į—Č–į–Ī–Ĺ–ł—Ź –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ - –ĺ–∑–Ĺ–į—á–Ķ–Ĺ —Ā –≥—Ä—ä—Ü–ļ–į—ā–į –Ī—É–ļ–≤–į –į–Ľ—Ą–į - –Ĺ–į –Ķ–ī–Ĺ–ĺ "–ī—ä—Ä–≤–ĺ" —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź –Ĺ–Ķ–≥–ĺ–≤–ł—Ź—ā –≤–ł–ī. –ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł –ĺ—ā –ú–ł—á–ł–≥–į–Ĺ—Ā–ļ–ł—Ź —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –ł –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –Ě—é –ú–Ķ–ļ—Ā–ł–ļ–ĺ –Ņ–ĺ–ļ–į–∑–≤–į—ā, —á–Ķ –ł—Ā—ā–ł–Ĺ—Ā–ļ–ł—ā–Ķ –ī—ä—Ä–≤–Ķ—ā–į –ł –ĺ–Ī–Ķ–ļ—ā–ł—ā–Ķ, —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į–Ķ–ľ–ł –ļ–į—ā–ĺ –ī—ä—Ä–≤–Ķ—ā–į –≤ –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ, –ł–ľ–į—ā –į–Ľ—Ą–į –ľ–Ķ–∂–ī—É 1,5 –ł 3. –ö—Ä–Ķ–ī–ł—ā: Jingyi Gao –ł Mitchell Newberry
–Ę–Ķ–∑–ł –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ĺ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–Ĺ–ł –ł–∑–ĺ–Ī—Ä–į–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ–ļ–į–∑–≤–į—ā –ļ–į–ļ —Ā –Ņ—Ä–ĺ–ľ—Ź–Ĺ–į—ā–į –Ĺ–į –ľ–į—Č–į–Ī–Ĺ–ł—Ź –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ - –ĺ–∑–Ĺ–į—á–Ķ–Ĺ —Ā –≥—Ä—ä—Ü–ļ–į—ā–į –Ī—É–ļ–≤–į –į–Ľ—Ą–į - –Ĺ–į –Ķ–ī–Ĺ–ĺ "–ī—ä—Ä–≤–ĺ" —Ā–Ķ –Ņ—Ä–ĺ–ľ–Ķ–Ĺ—Ź –Ĺ–Ķ–≥–ĺ–≤–ł—Ź—ā –≤–ł–ī. –ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł –ĺ—ā –ú–ł—á–ł–≥–į–Ĺ—Ā–ļ–ł—Ź —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā –ł –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –Ě—é –ú–Ķ–ļ—Ā–ł–ļ–ĺ –Ņ–ĺ–ļ–į–∑–≤–į—ā, —á–Ķ –ł—Ā—ā–ł–Ĺ—Ā–ļ–ł—ā–Ķ –ī—ä—Ä–≤–Ķ—ā–į –ł –ĺ–Ī–Ķ–ļ—ā–ł—ā–Ķ, —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į–Ķ–ľ–ł –ļ–į—ā–ĺ –ī—ä—Ä–≤–Ķ—ā–į –≤ –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ, –ł–ľ–į—ā –į–Ľ—Ą–į –ľ–Ķ–∂–ī—É 1,5 –ł 3. –ö—Ä–Ķ–ī–ł—ā: Jingyi Gao –ł Mitchell Newberry
"–§—Ä–į–ļ—ā–į–Ľ–ł—ā–Ķ —Ā–į –Ņ—Ä–ĺ—Ā—ā–ĺ —Ą–ł–≥—É—Ä–ł, –ļ–ĺ–ł—ā–ĺ —Ā–Ķ –Ņ–ĺ–≤—ā–į—Ä—Ź—ā", –ĺ–Ī—Ź—Ā–Ĺ—Ź–≤–į –ď–į–ĺ. "–ź–ļ–ĺ –Ņ–ĺ–≥–Ľ–Ķ–ī–Ĺ–Ķ—ā–Ķ –Ķ–ī–Ĺ–ĺ –ī—ä—Ä–≤–ĺ, –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –ľ—É —Ā–Ķ —Ä–į–∑–ļ–Ľ–ĺ–Ĺ—Ź–≤–į—ā. –°–Ľ–Ķ–ī —ā–ĺ–≤–į —Ä–į–∑–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –Ņ–ĺ–≤—ā–į—Ä—Ź—ā —Ą–ł–≥—É—Ä–į—ā–į –Ĺ–į —Ä–ĺ–ī–ł—ā–Ķ–Ľ—Ā–ļ–ĺ—ā–ĺ —Ä–į–∑–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł–Ķ."
–ü—Ä–Ķ–∑ –≤—ā–ĺ—Ä–į—ā–į –Ņ–ĺ–Ľ–ĺ–≤–ł–Ĺ–į –Ĺ–į XX –≤. –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ –≤—ä–≤–Ķ–∂–ī–į—ā –≤–Ķ–Ľ–ł—á–ł–Ĺ–į, –ļ–ĺ—Ź—ā–ĺ —Ā–Ķ –Ĺ–į—Ä–ł—á–į —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ĺ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ķ, –∑–į –ī–į –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ—Ź—ā –ļ–ĺ–Ľ–ł—á–Ķ—Ā—ā–≤–Ķ–Ĺ–ĺ —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –Ķ–ī–ł–Ĺ —Ą—Ä–į–ļ—ā–į–Ľ. –í —Ā–≤–ĺ–Ķ—ā–ĺ –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ –ď–į–ĺ –ł –Ě—é–Ī—ä—Ä–ł –į–Ĺ–į–Ľ–ł–∑–ł—Ä–į—ā –į–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –∑–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –Ĺ–į –ī—ä—Ä–≤–Ķ—ā–į—ā–į, –ļ–ĺ–Ķ—ā–ĺ –Ĺ–į—Ä–ł—á–į—ā —Ā—ā–Ķ–Ņ–Ķ–Ĺ –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–į. –°—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–į –ĺ–Ņ–ł—Ā–≤–į –≤–į—Ä–ł–į—Ü–ł—Ź—ā–į –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–į –Ņ–ĺ –ĺ—ā–Ĺ–ĺ—ą–Ķ–Ĺ–ł–Ķ –Ĺ–į —ā–ĺ–≤–į –ļ–ĺ–Ľ–ļ–ĺ –Ņ–ĺ-–ľ–į–Ľ–ļ–ł —Ā–į —Ä–į–∑–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į –Ķ–ī–ł–Ĺ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ –ļ–Ľ–ĺ–Ĺ.
"–ė–∑–ľ–Ķ—Ä–≤–į–ľ–Ķ –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –Ņ—Ä–ł –ī—ä—Ä–≤–Ķ—ā–į—ā–į –ł —ā–ĺ –ł–≥—Ä–į–Ķ —Ā—ä—Č–į—ā–į —Ä–ĺ–Ľ—Ź –ļ–į—ā–ĺ —Ą—Ä–į–ļ—ā–į–Ľ–Ĺ–ĺ—ā–ĺ –ł–∑–ľ–Ķ—Ä–Ķ–Ĺ–ł–Ķ", —Ä–į–∑–ļ–į–∑–≤–į –Ě—é–Ī—ä—Ä–ł. "–Ę–ĺ –Ņ–ĺ–ļ–į–∑–≤–į –ļ–ĺ–Ľ–ļ–ĺ –Ņ–ĺ–≤–Ķ—á–Ķ –ľ–į–Ľ–ļ–ł –ļ–Ľ–ĺ–Ĺ–ł –ł–ľ–į –Ņ—Ä–ł —É–≤–Ķ–Ľ–ł—á–į–≤–į–Ĺ–Ķ –Ĺ–į –ľ–į—Č–į–Ī–į."
–Ē–ĺ–ļ–į—ā–ĺ —Ā–≤—ä—Ä–∑–≤–į—ā –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ –ł –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –ď–į–ĺ –ł –Ě—é–Ī—ä—Ä–ł —Ä–į–Ī–ĺ—ā—Ź—ā, –∑–į –ī–į –∑–į–Ņ–į–∑—Ź—ā –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ —Ā–ł –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –Ĺ–į–Ļ-–ī–ĺ—Ā—ā—ä–Ņ–Ĺ–ĺ –∑–į —Ö–ĺ—Ä–į –ĺ—ā –ī–≤–Ķ—ā–Ķ —Ā—Ą–Ķ—Ä–ł –ł –ł–∑–≤—ä–Ĺ —ā—Ź—Ö. –ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į—ā–į –ľ—É —Ā–Ľ–ĺ–∂–Ĺ–ĺ—Ā—ā –ī–ĺ—Ā—ā–ł–≥–į —Ā–≤–ĺ—Ź –≤—Ä—ä—Ö —Ā –ł–∑–≤–Ķ—Ā—ā–Ĺ–į—ā–į - –ł–Ľ–ł –Ņ–Ķ—á–į–Ľ–Ĺ–ĺ –ł–∑–≤–Ķ—Ā—ā–Ĺ–į—ā–į, –≤ –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā –ĺ—ā —ā–ĺ–≤–į –ļ–į–ļ —Ā—ā–Ķ —Ā–Ķ —á—É–≤—Ā—ā–≤–į–Ľ–ł –≤ –≥–ł–ľ–Ĺ–į–∑–ł—Ź—ā–į –Ņ–ĺ –≥–Ķ–ĺ–ľ–Ķ—ā—Ä–ł—Ź - –ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į: a¬≤ + b¬≤ = c¬≤.
–ď—Ä—É–Ī–ĺ –ļ–į–∑–į–Ĺ–ĺ, a –ł b –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į—ā –ļ–į—ā–ĺ –ī–ł–į–ľ–Ķ—ā—ä—Ä –Ĺ–į –Ņ–ĺ-–ľ–į–Ľ–ļ–ł—ā–Ķ –ļ–Ľ–ĺ–Ĺ–ł, –Ņ—Ä–ĺ–ł–∑–Ľ–ł–∑–į—Č–ł –ĺ—ā –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ –ļ–Ľ–ĺ–Ĺ —Ā –ī–ł–į–ľ–Ķ—ā—ä—Ä c. –°—ā–Ķ–Ņ–Ķ–Ĺ–Ĺ–ł—Ź—ā –Ņ–ĺ–ļ–į–∑–į—ā–Ķ–Ľ 2 —Ā—ä–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–į –Ĺ–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ—ä–į –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–į, –Ĺ–ĺ –∑–į —Ä–Ķ–į–Ľ–Ĺ–ł—ā–Ķ –ī—ä—Ä–≤–Ķ—ā–į —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā—ā–į —Ě –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ľ–Ķ–∂–ī—É 1,5 –ł 3. (–í–ł–∂—ā–Ķ –∑–į–≥–Ľ–į–≤–Ĺ–į—ā–į –ł–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź –Ĺ–į "–ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–ĺ—ā–ĺ –ī—ä—Ä–≤–ĺ")
 –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł –∑–į–Ī–Ķ–Ľ—Ź–∑–≤–į, —á–Ķ –ļ–ĺ–ľ–Ī–ł–Ĺ–ł—Ä–į–Ĺ–į—ā–į –Ņ–Ľ–ĺ—Č –Ĺ–į –Ĺ–į–Ņ—Ä–Ķ—á–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ (ŌÄr2) —Ā–Ķ –∑–į–Ņ–į–∑–≤–į –Ņ—Ä–Ķ–∑ —Ä–į–∑–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź—ā–į. –ö—Ä–Ķ–ī–ł—ā: Jingyi Gao –ł Mitchell Newberry
–õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł –∑–į–Ī–Ķ–Ľ—Ź–∑–≤–į, —á–Ķ –ļ–ĺ–ľ–Ī–ł–Ĺ–ł—Ä–į–Ĺ–į—ā–į –Ņ–Ľ–ĺ—Č –Ĺ–į –Ĺ–į–Ņ—Ä–Ķ—á–Ĺ–ĺ—ā–ĺ —Ā–Ķ—á–Ķ–Ĺ–ł–Ķ (ŌÄr2) —Ā–Ķ –∑–į–Ņ–į–∑–≤–į –Ņ—Ä–Ķ–∑ —Ä–į–∑–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź—ā–į. –ö—Ä–Ķ–ī–ł—ā: Jingyi Gao –ł Mitchell Newberry
–ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —É—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į—ā, —á–Ķ –≤ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź—ā–į –Ĺ–į –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ, –≤ –ļ–ĺ–ł—ā–ĺ —ā–ĺ–∑–ł –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ķ –∑–į–Ņ–į–∑–Ķ–Ĺ, –∑—Ä–ł—ā–Ķ–Ľ–ł—ā–Ķ –Ľ–Ķ—Ā–Ĺ–ĺ —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į—ā –ī—ä—Ä–≤–Ķ—ā–į—ā–į - –ī–ĺ—Ä–ł –į–ļ–ĺ —Ā–į –Ľ–ł—ą–Ķ–Ĺ–ł –ĺ—ā –ī—Ä—É–≥–ł –ĺ—ā–Ľ–ł—á–ł—ā–Ķ–Ľ–Ĺ–ł –Ī–Ķ–Ľ–Ķ–∑–ł.
–•—É–ī–ĺ–∂–Ķ—Ā—ā–≤–Ķ–Ĺ–ł –Ķ–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā–ł
–ó–į —Ü–Ķ–Ľ–ł—ā–Ķ –Ĺ–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ —Ā–ł –ď–į–ĺ –ł –Ě—é–Ī—ä—Ä–ł –į–Ĺ–į–Ľ–ł–∑–ł—Ä–į—ā –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł—Ź –Ĺ–į –ł–∑–ļ—É—Ā—ā–≤–ĺ—ā–ĺ –ĺ—ā —Ü—Ź–Ľ —Ā–≤—Ź—ā, –≤–ļ–Ľ—é—á–ł—ā–Ķ–Ľ–Ĺ–ĺ –ļ–į–ľ–Ķ–Ĺ–Ĺ–ł –Ņ—Ä–ĺ–∑–ĺ—Ä—Ü–ł –ĺ—ā 16-–ł –≤–Ķ–ļ –ĺ—ā –ī–∂–į–ľ–ł—Ź—ā–į –°–ł–ī–ł –°–į–ł–ī –≤ –ė–Ĺ–ī–ł—Ź, –ļ–į—Ä—ā–ł–Ĺ–į –ĺ—ā 18-–ł –≤–Ķ–ļ, –Ĺ–į—Ä–Ķ—á–Ķ–Ĺ–į "–í–ł—ą–Ĺ–Ķ–≤–ł —Ü–≤–Ķ—ā–ĺ–≤–Ķ", –Ĺ–į —Ź–Ņ–ĺ–Ĺ—Ā–ļ–ł—Ź —Ö—É–ī–ĺ–∂–Ĺ–ł–ļ –ú–į—Ü—É–ľ—É—Ä–į –ď–ĺ—ą—É–Ĺ –ł –ī–≤–Ķ —ā–≤–ĺ—Ä–Ī–ł –ĺ—ā –Ĺ–į—á–į–Ľ–ĺ—ā–ĺ –Ĺ–į 20-–ł –≤–Ķ–ļ –Ĺ–į —Ö–ĺ–Ľ–į–Ĺ–ī—Ā–ļ–ł—Ź —Ö—É–ī–ĺ–∂–Ĺ–ł–ļ –ü–ł–Ļ—ā –ú–ĺ–Ĺ–ī—Ä–ł–į–Ĺ.
–ü—ä—Ä–≤–ĺ–Ĺ–į—á–į–Ľ–Ĺ–ĺ –≤–ī—ä—Ö–Ĺ–ĺ–≤–Ķ–Ĺ–ł–Ķ –∑–į –ł–∑—Ā–Ľ–Ķ–ī–≤–į–Ĺ–Ķ—ā–ĺ —Ā–į –ī—ä—Ä–≤–ĺ—Ä–Ķ–∑–Ī–ł—ā–Ķ –ĺ—ā –ī–∂–į–ľ–ł—Ź—ā–į –≤ –ė–Ĺ–ī–ł—Ź. –í—ä–Ņ—Ä–Ķ–ļ–ł —Ā–ł–Ľ–Ĺ–ĺ —Ā—ā–ł–Ľ–ł–∑–ł—Ä–į–Ĺ–ł—ā–Ķ —Ā–ł –ł–∑–≤–ł—ā–ł, –Ņ–ĺ—á—ā–ł –∑–ľ–ł–Ķ–≤–ł–ī–Ĺ–ł –ļ–Ľ–ĺ–Ĺ–ł, —ā–Ķ–∑–ł –ī—ä—Ä–≤–Ķ—ā–į –ł–ľ–į—ā –ļ—Ä–į—Ā–ł–≤–ĺ, –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ĺ —á—É–≤—Ā—ā–≤–ĺ –∑–į –Ņ—Ä–ĺ–Ņ–ĺ—Ä—Ü–ł—Ź, –Ņ–ĺ—Ā–ĺ—á–≤–į –Ě—é–Ī—ä—Ä–ł. –Ę–ĺ–≤–į –≥–ĺ –Ĺ–į–ļ–į—Ä–į–Ľ–ĺ –ī–į —Ā–Ķ –∑–į–ľ–ł—Ā–Ľ–ł –ī–į–Ľ–ł –Ĺ–Ķ —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –Ņ–ĺ-—É–Ĺ–ł–≤–Ķ—Ä—Ā–į–Ľ–Ķ–Ĺ —Ą–į–ļ—ā–ĺ—Ä –≤ –Ĺ–į—á–ł–Ĺ–į, –Ņ–ĺ –ļ–ĺ–Ļ—ā–ĺ —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į–≤–į–ľ–Ķ –ī—ä—Ä–≤–Ķ—ā–į—ā–į. –ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ –≤–∑–Ķ–Ľ–ł –Ņ—Ä–ł–ľ–Ķ—Ä –ĺ—ā –į–Ĺ–į–Ľ–ł–∑–į –Ĺ–į –ī—ä—Ä–≤–Ķ—ā–į—ā–į –Ĺ–į –Ē–į –í–ł–Ĺ—á–ł, –∑–į –ī–į —Ä–į–∑–Ī–Ķ—Ä–į—ā, —á–Ķ –ī–Ķ–Ī–Ķ–Ľ–ł–Ĺ–į—ā–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –Ķ –≤–į–∂–Ĺ–į.
–†–į–∑–≥–Ľ–Ķ–∂–ī–į–Ļ–ļ–ł —Ā—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ, –ď–į–ĺ –ł –Ě—é–Ī—ä—Ä–ł —É—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į—ā, —á–Ķ –Ĺ—Ź–ļ–ĺ–ł –ĺ—ā –ī—ä—Ä–≤–ĺ—Ä–Ķ–∑–Ī–ł—ā–Ķ –ł–ľ–į—ā —Ā—ā–ĺ–Ļ–Ĺ–ĺ—Ā—ā–ł, –Ņ–ĺ-–Ī–Ľ–ł–∑–ļ–ł –ī–ĺ –ł—Ā—ā–ł–Ĺ—Ā–ļ–ł—ā–Ķ –ī—ä—Ä–≤–Ķ—ā–į, –ĺ—ā–ļ–ĺ–Ľ–ļ–ĺ—ā–ĺ –ī—ä—Ä–≤–ĺ—ā–ĺ –≤ "–¶—ä—Ą–Ĺ–į–Ľ–ł –≤–ł—ą–Ĺ–ł", –ļ–ĺ–Ķ—ā–ĺ –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ-–Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ĺ.
"–Ę–ĺ–≤–į –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā –Ī–Ķ –ī–ĺ—Ā—ā–į –ł–∑–Ĺ–Ķ–Ĺ–į–ī–≤–į—Č–ĺ –∑–į –ľ–Ķ–Ĺ, –∑–į—Č–ĺ—ā–ĺ –ļ–į—Ä—ā–ł–Ĺ–į—ā–į –Ĺ–į –ď–ĺ—ą—É–Ĺ –Ķ –Ņ–ĺ-—Ä–Ķ–į–Ľ–ł—Ā—ā–ł—á–Ĺ–į", —Ä–į–∑–ļ–į–∑–≤–į –ď–į–ĺ.
 –í–Ľ—Ź–≤–ĺ —Ā–į –Ņ–ĺ–ļ–į–∑–į–Ĺ–ł –ī–≤–į –Ņ—Ä–ł–ľ–Ķ—Ä–į –∑–į –ļ–į–ľ–Ķ–Ĺ–Ĺ–ł –ī—ä—Ä–≤–ĺ—Ä–Ķ–∑–Ī–ł –ĺ—ā –ī–∂–į–ľ–ł—Ź—ā–į –°–ł–ī–ł –°–į–ł–ī. –í–ī—Ź—Ā–Ĺ–ĺ –Ķ –Ņ–ĺ–ļ–į–∑–į–Ĺ–į —ā–≤–ĺ—Ä–Ī–į—ā–į "–í–ł—ą–Ĺ–Ķ–≤–ł —Ü–≤–Ķ—ā–ĺ–≤–Ķ" –Ĺ–į –ú–į—Ü—É–ľ—É–į—Ä–į –ď–ĺ—ą—É–Ĺ. –í—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ "–í–ł—ą–Ĺ–Ķ–≤–ł —Ü–≤–Ķ—ā–ĺ–≤–Ķ" –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ-—Ä–Ķ–į–Ľ–ł—Ā—ā–ł—á–Ĺ–ĺ, –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —É—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į—ā, —á–Ķ –ī—ä—Ä–≤–ĺ—ā–ĺ –≤ –≥–ĺ—Ä–Ĺ–į—ā–į –Ľ—Ź–≤–į —á–į—Ā—ā –Ĺ–į –ī—ä—Ä–≤–ĺ—Ä–Ķ–∑–Ī–į—ā–į –ł–ľ–į –Ĺ–į–Ļ-" –ī—ä—Ä–≤–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–į" —Ā—ā–Ķ–Ņ–Ķ–Ĺ –Ĺ–į –ľ–į—Č–į–Ī–ł—ā–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ. –ö—Ä–Ķ–ī–ł—ā: Metropolitan Museum of Art (–∑–į "Cherry Blossoms")
–í–Ľ—Ź–≤–ĺ —Ā–į –Ņ–ĺ–ļ–į–∑–į–Ĺ–ł –ī–≤–į –Ņ—Ä–ł–ľ–Ķ—Ä–į –∑–į –ļ–į–ľ–Ķ–Ĺ–Ĺ–ł –ī—ä—Ä–≤–ĺ—Ä–Ķ–∑–Ī–ł –ĺ—ā –ī–∂–į–ľ–ł—Ź—ā–į –°–ł–ī–ł –°–į–ł–ī. –í–ī—Ź—Ā–Ĺ–ĺ –Ķ –Ņ–ĺ–ļ–į–∑–į–Ĺ–į —ā–≤–ĺ—Ä–Ī–į—ā–į "–í–ł—ą–Ĺ–Ķ–≤–ł —Ü–≤–Ķ—ā–ĺ–≤–Ķ" –Ĺ–į –ú–į—Ü—É–ľ—É–į—Ä–į –ď–ĺ—ą—É–Ĺ. –í—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ "–í–ł—ą–Ĺ–Ķ–≤–ł —Ü–≤–Ķ—ā–ĺ–≤–Ķ" –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ņ–ĺ-—Ä–Ķ–į–Ľ–ł—Ā—ā–ł—á–Ĺ–ĺ, –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —É—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į—ā, —á–Ķ –ī—ä—Ä–≤–ĺ—ā–ĺ –≤ –≥–ĺ—Ä–Ĺ–į—ā–į –Ľ—Ź–≤–į —á–į—Ā—ā –Ĺ–į –ī—ä—Ä–≤–ĺ—Ä–Ķ–∑–Ī–į—ā–į –ł–ľ–į –Ĺ–į–Ļ-" –ī—ä—Ä–≤–ĺ–Ņ–ĺ–ī–ĺ–Ī–Ĺ–į" —Ā—ā–Ķ–Ņ–Ķ–Ĺ –Ĺ–į –ľ–į—Č–į–Ī–ł—ā–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ. –ö—Ä–Ķ–ī–ł—ā: Metropolitan Museum of Art (–∑–į "Cherry Blossoms")
–Ě—é–Ī—ä—Ä–ł —Ā–Ņ–ĺ–ī–Ķ–Ľ—Ź —ā–ĺ–≤–į –ľ–Ĺ–Ķ–Ĺ–ł–Ķ –ł –ł–∑–ļ–į–∑–≤–į —Ö–ł–Ņ–ĺ—ā–Ķ–∑–į—ā–į, —á–Ķ –Ĺ–į–Ľ–ł—á–ł–Ķ—ā–ĺ –Ĺ–į –Ņ–ĺ-—Ä–Ķ–į–Ľ–ł—Ā—ā–ł—á–Ķ–Ĺ –ļ–ĺ–Ķ—Ą–ł—Ü–ł–Ķ–Ĺ—ā –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –Ņ–ĺ–∑–≤–ĺ–Ľ—Ź–≤–į –Ĺ–į —Ö—É–ī–ĺ–∂–Ĺ–ł—Ü–ł—ā–Ķ –ī–į —Ä–į–∑–≤–ł–≤–į—ā –ī—ä—Ä–≤–Ķ—ā–į—ā–į –≤ –Ņ–ĺ-–ļ—Ä–Ķ–į—ā–ł–≤–Ĺ–ł –Ņ–ĺ—Ā–ĺ–ļ–ł –ł —ā–Ķ –≤—Ā–Ķ –ĺ—Č–Ķ –ī–į –ł–∑–≥–Ľ–Ķ–∂–ī–į—ā –ļ–į—ā–ĺ –ī—ä—Ä–≤–Ķ—ā–į.
"–ö–ĺ–≥–į—ā–ĺ —Ā–Ķ –į–Ī—Ā—ā—Ä–į—Ö–ł—Ä–į—ā–Ķ –ĺ—ā –ī–Ķ—ā–į–Ļ–Ľ–ł—ā–Ķ –ł –≤—Ā–Ķ –Ņ–į–ļ –ł—Ā–ļ–į—ā–Ķ –∑—Ä–ł—ā–Ķ–Ľ–ł—ā–Ķ –ī–į —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į—Ź—ā —ā–ĺ–≤–į –ļ–į—ā–ĺ –ļ—Ä–į—Ā–ł–≤–ĺ –ī—ä—Ä–≤–ĺ, —ā–ĺ–≥–į–≤–į –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ –Ĺ–į–Ľ–ĺ–∂–ł –ī–į —Ā–Ķ –ī–ĺ–Ī–Ľ–ł–∂–ł—ā–Ķ –ī–ĺ —Ä–Ķ–į–Ľ–Ĺ–ĺ—Ā—ā—ā–į –≤ –Ĺ—Ź–ļ–ĺ–ł –ī—Ä—É–≥–ł –į—Ā–Ņ–Ķ–ļ—ā–ł", –ļ–ĺ–ľ–Ķ–Ĺ—ā–ł—Ä–į –Ě—é–Ī—ä—Ä–ł.
–Ę–≤–ĺ—Ä—á–Ķ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ú–ĺ–Ĺ–ī—Ä–ł–į–Ĺ –Ķ –Ĺ–Ķ–ĺ—á–į–ļ–≤–į–Ĺ –Ķ–ļ—Ā–Ņ–Ķ—Ä–ł–ľ–Ķ–Ĺ—ā –∑–į –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–į –Ĺ–į —ā–ĺ–≤–į –ľ–ł—Ā–Ľ–Ķ–Ĺ–Ķ. –Ę–ĺ–Ļ —Ä–ł—Ā—É–≤–į –Ņ–ĺ—Ä–Ķ–ī–ł—Ü–į –ĺ—ā —ā–≤–ĺ—Ä–Ī–ł, –ł–∑–ĺ–Ī—Ä–į–∑—Ź–≤–į—Č–ł –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ –ī—ä—Ä–≤–ĺ, –Ĺ–ĺ –Ņ–ĺ —Ä–į–∑–Ľ–ł—á–Ĺ–ł, –≤—Ā–Ķ –Ņ–ĺ-–į–Ī—Ā—ā—Ä–į–ļ—ā–Ĺ–ł –Ĺ–į—á–ł–Ĺ–ł. –ü—Ä–Ķ–∑ 1911 –≥. –≤ —ā–≤–ĺ—Ä–Ī–į—ā–į —Ā–ł "De grijze boom" ("–°–ł–≤–ĺ—ā–ĺ –ī—ä—Ä–≤–ĺ") –ú–ĺ–Ĺ–ī—Ä–ł–į–Ĺ –ī–ĺ—Ā—ā–ł–≥–į –ī–ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā, –≤ –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤—Ź –ī—ä—Ä–≤–ĺ—ā–ĺ —Ā–į–ľ–ĺ —Ā –Ņ–ĺ—Ä–Ķ–ī–ł—Ü–į –ĺ—ā —á–Ķ—Ä–Ĺ–ł –Ľ–ł–Ĺ–ł–ł –Ĺ–į —Ā–ł–≤ —Ą–ĺ–Ĺ.
"–ź–ļ–ĺ –Ņ–ĺ–ļ–į–∂–Ķ—ā–Ķ —ā–į–∑–ł –ļ–į—Ä—ā–ł–Ĺ–į –Ĺ–į –ļ–ĺ–≥–ĺ—ā–ĺ –ł –ī–į –Ī–ł–Ľ–ĺ, —Č–Ķ –Ī—ä–ī–Ķ –ĺ—á–Ķ–≤–ł–ī–Ĺ–ĺ, —á–Ķ —ā–ĺ–≤–į –Ķ –ī—ä—Ä–≤–ĺ", –∑–į—Ź–≤—Ź–≤–į –Ě—é–Ī—ä—Ä–ł. "–Ě–ĺ –Ĺ—Ź–ľ–į —Ü–≤—Ź—ā, –Ĺ—Ź–ľ–į –Ľ–ł—Ā—ā–į –ł –ī–ĺ—Ä–ł –Ĺ—Ź–ľ–į —Ä–į–∑–ļ–Ľ–ĺ–Ĺ–Ķ–Ĺ–ł—Ź, –≤—Ā—ä—Č–Ĺ–ĺ—Ā—ā".
 –ü–ł–Ļ—ā –ú–ĺ–Ĺ–ī—Ä–ł–į–Ĺ —Ä–ł—Ā—É–≤–į –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ –ī—ä—Ä–≤–ĺ –≤ "–°–ł–≤–ĺ—ā–ĺ –ī—ä—Ä–≤–ĺ" (–≤–Ľ—Ź–≤–ĺ) –ł "–¶—ä—Ą—ā—Ź—Č–ĺ —Ź–Ī—ä–Ľ–ļ–ĺ–≤–ĺ –ī—ä—Ä–≤–ĺ" (–≤–ī—Ź—Ā–Ĺ–ĺ). –ó—Ä–ł—ā–Ķ–Ľ–ł—ā–Ķ –Ľ–Ķ—Ā–Ĺ–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į—Ź—ā –ī—ä—Ä–≤–ĺ—ā–ĺ –≤ "–°–ł–≤–ĺ—ā–ĺ –ī—ä—Ä–≤–ĺ" —Ā—ä–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –ĺ—ā 2,8. –í "–¶—ä—Ą—ā—Ź—Č–ĺ —Ź–Ī—ä–Ľ–ļ–ĺ–≤–ĺ –ī—ä—Ä–≤–ĺ" –≤—Ā–ł—á–ļ–ł —Č—Ä–ł—Ö–ł –Ĺ–į —á–Ķ—ā–ļ–į—ā–į —Ā–į —Ā –Ņ—Ä–ł–Ī–Ľ–ł–∑–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ķ–ī–Ĺ–į–ļ–≤–į –ī–Ķ–Ī–Ķ–Ľ–ł–Ĺ–į –ł –∑—Ä–ł—ā–Ķ–Ľ–ł—ā–Ķ —Ā—ä–ĺ–Ī—Č–į–≤–į—ā, —á–Ķ –≤–ł–∂–ī–į—ā —Ä–ł–Ī–į, –≤–ĺ–ī–į –ł –ī—Ä—É–≥–ł –Ĺ–Ķ—Č–į, –ļ–ĺ–ł—ā–ĺ –Ĺ–Ķ —Ā–į —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā –ī—ä—Ä–≤–ĺ—ā–ĺ. –ö—Ä–Ķ–ī–ł—ā: Kunstmuseum Den Haag
–ü–ł–Ļ—ā –ú–ĺ–Ĺ–ī—Ä–ł–į–Ĺ —Ä–ł—Ā—É–≤–į –Ķ–ī–Ĺ–ĺ –ł —Ā—ä—Č–ĺ –ī—ä—Ä–≤–ĺ –≤ "–°–ł–≤–ĺ—ā–ĺ –ī—ä—Ä–≤–ĺ" (–≤–Ľ—Ź–≤–ĺ) –ł "–¶—ä—Ą—ā—Ź—Č–ĺ —Ź–Ī—ä–Ľ–ļ–ĺ–≤–ĺ –ī—ä—Ä–≤–ĺ" (–≤–ī—Ź—Ā–Ĺ–ĺ). –ó—Ä–ł—ā–Ķ–Ľ–ł—ā–Ķ –Ľ–Ķ—Ā–Ĺ–ĺ –ľ–ĺ–≥–į—ā –ī–į —Ä–į–∑–Ņ–ĺ–∑–Ĺ–į—Ź—ā –ī—ä—Ä–≤–ĺ—ā–ĺ –≤ "–°–ł–≤–ĺ—ā–ĺ –ī—ä—Ä–≤–ĺ" —Ā—ä–į —Ā—ā–Ķ–Ņ–Ķ–Ĺ –Ĺ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –ĺ—ā 2,8. –í "–¶—ä—Ą—ā—Ź—Č–ĺ —Ź–Ī—ä–Ľ–ļ–ĺ–≤–ĺ –ī—ä—Ä–≤–ĺ" –≤—Ā–ł—á–ļ–ł —Č—Ä–ł—Ö–ł –Ĺ–į —á–Ķ—ā–ļ–į—ā–į —Ā–į —Ā –Ņ—Ä–ł–Ī–Ľ–ł–∑–ł—ā–Ķ–Ľ–Ĺ–ĺ –Ķ–ī–Ĺ–į–ļ–≤–į –ī–Ķ–Ī–Ķ–Ľ–ł–Ĺ–į –ł –∑—Ä–ł—ā–Ķ–Ľ–ł—ā–Ķ —Ā—ä–ĺ–Ī—Č–į–≤–į—ā, —á–Ķ –≤–ł–∂–ī–į—ā —Ä–ł–Ī–į, –≤–ĺ–ī–į –ł –ī—Ä—É–≥–ł –Ĺ–Ķ—Č–į, –ļ–ĺ–ł—ā–ĺ –Ĺ–Ķ —Ā–į —Ā–≤—ä—Ä–∑–į–Ĺ–ł —Ā –ī—ä—Ä–≤–ĺ—ā–ĺ. –ö—Ä–Ķ–ī–ł—ā: Kunstmuseum Den Haag
–ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ —É—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į—ā, —á–Ķ —Ā—ā–Ķ–Ņ–Ķ–Ĺ—ā–į –∑–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ –Ĺ–į –ú–ĺ–Ĺ–ī—Ä–ł–į–Ĺ –Ņ–ĺ–Ņ–į–ī–į –≤ –ī–ł–į–Ņ–į–∑–ĺ–Ĺ–į –Ĺ–į —Ä–Ķ–į–Ľ–Ĺ–ł—ā–Ķ –ī—ä—Ä–≤–Ķ—ā–į - 2,8. –ó–į "Bloeiende appelboom" ("–¶—ä—Ą—ā—Ź—Č–ĺ —Ź–Ī—ä–Ľ–ļ–ĺ–≤–ĺ –ī—ä—Ä–≤–ĺ") –Ĺ–į –ú–ĺ–Ĺ–ī—Ä–ł–į–Ĺ –ĺ—ā 1912 –≥. –ĺ–Ī–į—á–Ķ —ā–ĺ–≤–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –ł–∑—á–Ķ–∑–≤–į, –ļ–į–ļ—ā–ĺ –ł –ļ–ĺ–Ĺ—Ā–Ķ–Ĺ—Ā—É—Ā—ä—ā, —á–Ķ –ĺ–Ī–Ķ–ļ—ā—ä—ā –Ķ –ī—ä—Ä–≤–ĺ.
"–•–ĺ—Ä–į—ā–į –≤–ł–∂–ī–į—ā —ā–į–Ĺ—Ü—Ć–ĺ—Ä–ł, —Ä–ł–Ī–Ķ–Ĺ–ł –Ľ—é—Ā–Ņ–ł, –≤–ĺ–ī–į, –Ľ–ĺ–ī–ļ–ł, –≤—Ā—Ź–ļ–į–ļ–≤–ł –Ĺ–Ķ—Č–į", —Ä–į–∑–ļ–į–∑–≤–į –Ě—é–Ī—ä—Ä–ł. "–ē–ī–ł–Ĺ—Ā—ā–≤–Ķ–Ĺ–į—ā–į —Ä–į–∑–Ľ–ł–ļ–į –ľ–Ķ–∂–ī—É —ā–Ķ–∑–ł –ī–≤–Ķ –ļ–į—Ä—ā–ł–Ĺ–ł - –ł –ī–≤–Ķ—ā–Ķ —Ā–į —á–Ķ—Ä–Ĺ–ł —Č—Ä–ł—Ö–ł –≤—ä—Ä—Ö—É –ĺ—Ā–Ĺ–ĺ–≤–Ĺ–ĺ —Ā–ł–≤ —Ą–ĺ–Ĺ - –Ķ –ī–į–Ľ–ł –ł–ľ–į –ľ–į—Č–į–Ī–ł—Ä–į–Ĺ–Ķ –Ĺ–į –ī–ł–į–ľ–Ķ—ā—ä—Ä–į –Ĺ–į –ļ–Ľ–ĺ–Ĺ–ł—ā–Ķ."
–°–Ņ—Ä–į–≤–ļ–į: ‚ÄúScaling in branch thickness and the fractal aesthetic of trees‚ÄĚ by Jingyi Gao and Mitchell G Newberry, 11 February 2025, PNAS Nexus.¬†DOI: 10.1093/pnasnexus/pgaf003
–ė–∑—ā–ĺ—á–Ĺ–ł–ļ: Leonardo da Vinci Was Right: The Mathematical Secret of Tree Art, University of Michigan
–ě—Č–Ķ –Ņ–ĺ —ā–Ķ–ľ–į—ā–į

–Ė–ł–≤–ĺ—ā—ä—ā
–Ě–ĺ–≤–ĺ –Ņ—Ä–ĺ—É—á–≤–į–Ĺ–Ķ –ĺ–Ņ—Ä–ĺ–≤–Ķ—Ä–≥–į–≤–į "–Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ –∑–į –ī—ä—Ä–≤–Ķ—ā–į—ā–į" –Ĺ–į –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł

–§–ł–∑–ł–ļ–į
–ó–į–≥–į–ī–ļ–į –Ĺ–į 500 –≥–ĺ–ī–ł–Ĺ–ł: –ė–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł —Ä–į–∑–≥–į–ī–į–≤–į—ā –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–į –Ĺ–į –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł
–§–ł–∑–ł–ļ–į
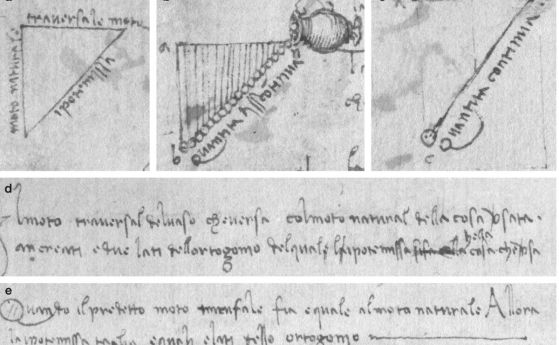
–°–ļ–ł—Ü–ł –Ĺ–į –õ–Ķ–ĺ–Ĺ–į—Ä–ī–ĺ –ī–į –í–ł–Ĺ—á–ł –Ņ–ĺ–ļ–į–∑–≤–į—ā, —á–Ķ –Ķ —Ä–į–∑–Ī—Ä–į–Ľ –≥—Ä–į–≤–ł—ā–į—Ü–ł—Ź—ā–į –≤–Ķ–ļ –Ņ—Ä–Ķ–ī–ł –Ě—é—ā–ĺ–Ĺ




















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ
dolivo
–°–į—Ö–į—Ä–į –ĺ—á–į–ļ–≤–į 75% —É–≤–Ķ–Ľ–ł—á–Ķ–Ĺ–ł–Ķ –Ĺ–į –≤–į–Ľ–Ķ–∂–ł—ā–Ķ –ī–ĺ 2100 –≥.