
Едно просто и нагледно доказателство на теоремата на Питагор представи математикът Андрес Навас от Университета на Сантяго де Чили.
Препринт на изследването е публикувано в сайта arXiv.org.
Питагоровата теорема гласи, че в правоъгълния триъгълник, квадратът на хипотенузата (най-голямата страна, намираща се срещу правия ъгъл) е равен на сумата от квадратите на катетите (две по-малки страни).
Досега има повече от 370 различни доказателства на теоремата. Освен самият Питагор, Евклид, Леонардо да Винчи, оригинално доказателство имат и Айншайн и дори един американски президент - Джеймс Гарфийлд.
Математикът не използва квадрати или подобни триъгълници, а теоремата на Уолъс-Бояй-Гервин, наречена на името на математиците Уилям Уолъс, Фаркаш Бояй и Пол Гервин. Теоремата е свързана с дисекция на многоъгълници - метод, при който чрез разрязване на един многоъгълник на парчета и пренареждането им да се получи друг многоъгълник чрез транслации и ротации. Теоремата на Уолъс-Бояй-Гервин гласи, че това може да стане единствено ако двата многоъгълника имат една и съща площ.
От равенството:
a2 + b2 = c2
следва, че площта на правилен n-ъгълник на страна c е равна на сумата от площите на двaта правилни n-ъгълници на страни a и b, съответно. За да се докаже това, е достатъчно да се умножат двете страни на равенството с подходяща константа (площта на правилния n-ъгълник разделена на дължина на страната). Всъщност, ако се докаже, че това твърдение е вярно за всяко n ≥ 3 , ще бъде еквивалентно на доказателство на теоремата Питагор.
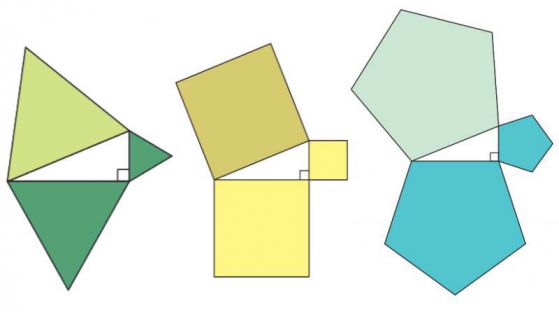
И разбира се, за да се докаже това, може да се използва теоремата на Уолъс-Бояй-Гервин - двата малки n-ъгълници да се разрежат на многоъгълни парчета, които след прегрупиране да получим един по-голям. Но броят на парчета може да бъде много голям.
Авторът предлага кратко геометрично доказателство на твърдението по-горе за равностранен триъгълник с помощта на една красива и и както изглежда незабелязана конфигурация.
Нека A, B, C са върховете на правоъгълен триъгълник. Завъртаме триъгълника ABC обратно на часовниковата стрелка на 60o около връх А и по часовниковата стрелка на 60o около B. Да наречем с C1, В1 и В2, А2 върховете, както е показано на чертежа долу. Забележете, че ВА2 = с = AB1 и ∠ABA2 = ∠BAB1 = 60o , следователно, А2 и В1 съвпадат и могат да се означи тази точка с D, върховете A, B и D определят равностранен триъгълник със страна с дължина с.
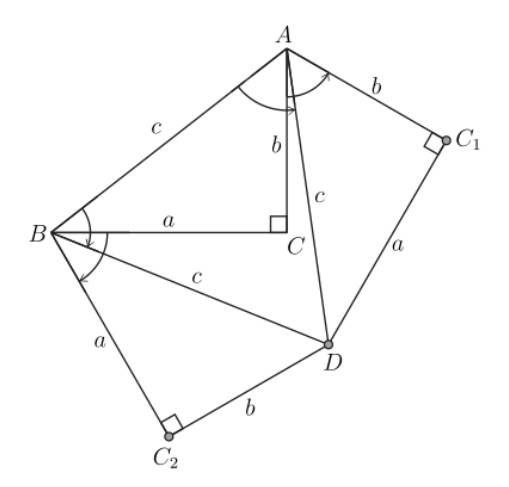
Също така, забележете, че BCC2 и ACC1 са равностранни триъгълници със страни с дължина a и b, съответно.
Нещо повече, двата триъгълника BC2D и AC1D са еднакви с триъгълника BCA.
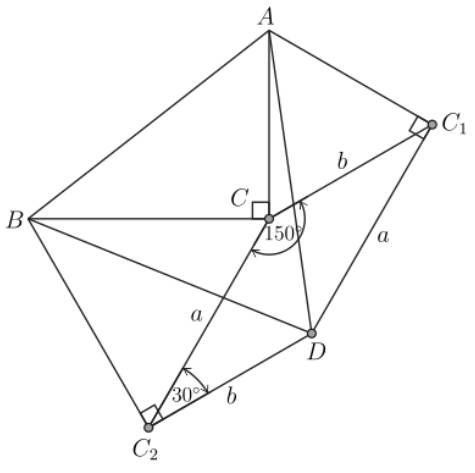
Навас изчислява площта на получения полигон:
ABC2DC1 = ABD + BC2D + AC1D = ACC1 + BCC2 + BCA + C2DC1C.
Като фигури,
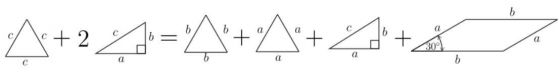
което е еквивалентно на:
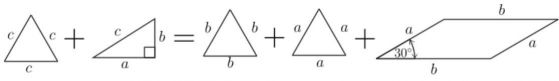
Остава да се докаже, че
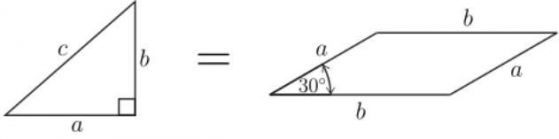
За да се направи това, забележете, че C2DC1C е успоредник със страни a и b. Освен това, както ∠BCA = 90o и имаме, че ∠C1CC2 трябва е равен на 120o.
Следователно ∠CC2D = ∠DC1C = 30 °
По този начин:
C1CC2D = ab sin (30°) = 1/2ab= ВСА.
Забележка: В последната стъпка може да се избегне използването на тригонометрията, ако разгледате схемите по-долу.
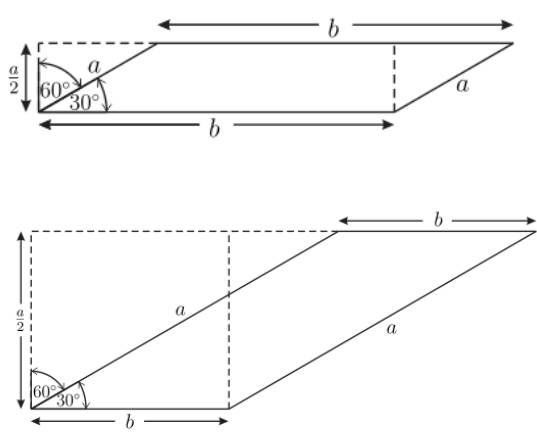
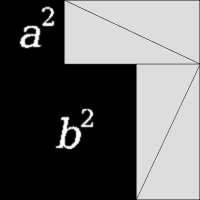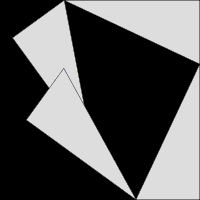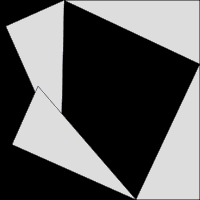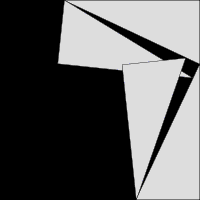
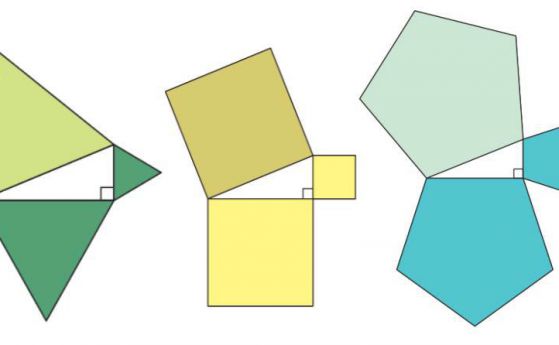
Ето още три доказателства с дисекция и пренареждане:

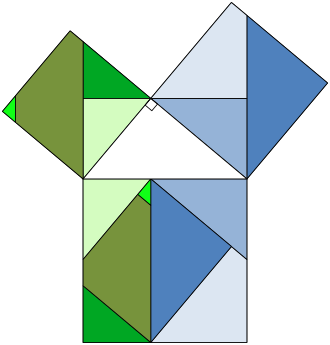























Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон