Дали математиката е „реална“ или нещо напълно умозрително?
Философи и математици спорят за това от векове. Някои вярват, че математиката е универсална - други я смятат за толкова реална, колкото всичко друго, което хората са измислили.
Даниел Мансфийлд (Daniel Mansfield), преподавател по математика в Университета на Нов Южен Уелс, Австралия, прави в The Conversation кратък обзор на представите на древните математици, търсейки отговор на тези въпроси.
От една гледна точка математиката е универсален език, използван за описание на света около нас. Например две ябълки плюс три ябълки винаги са пет ябълки, независимо от гледната точка.
Но математиката също е език, използван от хората, така че не е независим от културата. Историята ни показва, че различните култури са имали собствено разбиране за математиката.
За съжаление, по-голямата част от това древно разбиране вече е загубено. Почти във всяка древна култура са останали няколко разпръснати текста, показващи научните им познания.
Има обаче една древна култура, която е оставила след себе си абсолютно изобилие от текстове.
Вавилонската алгебра
Погребани в пустините на съвременен Ирак, глинените плочки от древен Вавилон оцеляват непокътнати около 4000 години.
Това, което научаваме от тези глинени таблички, е, че вавилонците са били практични хора, които са били много добри в сметките и са знаели как да решават сложни проблеми с числата.
Тяхната аритметика обаче е била различна от нашата. Те не са използвали нула или отрицателни числа. Те дори са определили движението на планетите, без да използват методите на съвременната математика.
Те са знаели, че числата 3, 4 и 5 съответстват на дължините на страните и диагонала на правоъгълник. Те също така са знаели, че тези числа отговарят на основната връзка 3² + 4² = 5², която гарантира, че страните на триъгълника са перпендикулярни.
Вавилонците са направили всичко това без съвременните алгебрични концепции. Сега изразяваме същата идея по-обобщено с помощта на Питагоровата теорема - във всеки правоъгълен триъгълник, дължината на катетите a и b и хипотенузата отговарят на зависимостта a² + b² = c².
Вавилонците са можели да решават квадратни уравнения, геометрични прогресии, употребявали са пропорции, средно аритметично, проценти.
Във вавилонските текстове, както и в египетските, се е представял само алгоритъма за решение с конкретни примери без променливи, теореми, аксиоми и доказателства, не защото са били глупави, а защото тези идеи все още не са били развити. Това са сравнително модерни понятия, които се появяват повече от 1000 години по-късно, в древна Гърция.
"Теоремата на Питагор" се появява за първи път (още от епохата на Хамурапи - XX век пр.н.е.) и то в общ вид. Тя е отразена в специални таблици и широко е използвана за решаване на различни задачи.
Вавилонската глинена плочка "Плимптон 322" от около 1800 г. пр. н. е. свидетелства за високото развитие на математиката в древна Месопотамия. Тя изобразява таблица от четири колони и петнадесет реда числа, написани в клинопис от този период. Втората и третата колона съдържат двойка числа от питагорейски тройки, т.е. числата a и c, така че да са в питагорейска тройка a² + b² = c². Например, първият ред съдържа числа, записани в шестдесетичната система като 1°59 и 2°49 (т.е. 119 и 169). Тъй като разликата между квадратите на тези числа е точен квадрат: 169² - 119² = 120², то тези числа образуват питагорейска тройка. Първата колона на тази таблица съдържа число, което може да се получи като c/b². Последната колона съдържа само номера на реда (от 1 до 15). Кредит: Wikimedia Commons
Питагоровата теорема
Как Питагор е измислил своята теорема. Краткият отговор е, че не го е направил.
Питагор от Самос (около 570-495 г. пр. н. е.) вероятно е чувал за идеята, която сега свързваме с неговото име, докато е бил в Египет. Може би той е бил човекът, който я е разпространил в Гърция, но и това не е сигурно.
Общоприето е, че доказателството за съотношенията в правоъгълния триъгълник е дадено от Питагор и че е използвал алгебрични методи за намиране на питагорейски тройки, но в същото време, в продължение на пет века след смъртта на Питагор, няма пряко споменаван за неговото авторство на доказателството. Но Плутарх и Цицерон пишат така за теоремата на Питагор, че сякаш авторството на Питагор е добре известно и несъмнено. Съществува и легенда,според която Питагор е ознаменувал откриването на своята теорема с грандиозен пир, убивайки сто бика.
Каквато и да е истината, Питагор не е използвал теоремата си за нищо практично. Той се интересува предимно от нумерологията и мистиката на числата, а не от приложенията на математиката.
Вавилонците, от друга страна, може би са използвали знанията си за правоъгълни триъгълници за по-конкретни цели. Съществуват доказателства от древна Индия и Рим, показващи, че пропорцията 3-4-5 е била използвана като прост, но ефективен начин за създаване на прави ъгли при изграждането на религиозни храмове и в геодезията.
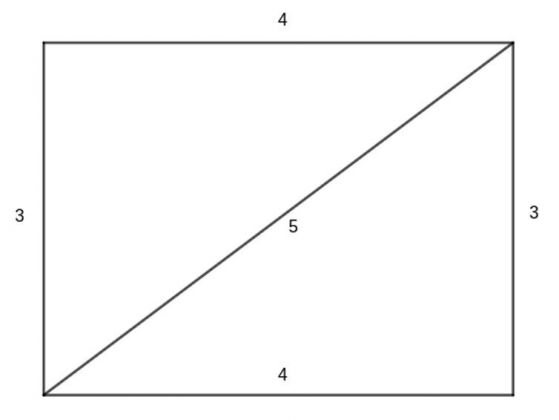
Как са построявали точни прави ъгли древните строители без съвременни инструменти?
Старите индуистки религиозни текстове дават инструкции за изработване на правоъгълен огнен олтар, използвайки пропорцията 3-4-5 на провоъгълник със страни 3 и 4 и диагонал с длжина 5. Тези измервания гарантират, че олтарът има прави ъгли във всеки ъгъл.
Но математиката в Древна Индия заслужава специално внимание.
Обсерваторията в Джейпур, Индия. Кредит: Wikimedia Commons
Невероятната Индия
Древните индийци, с високата си интелигентност и склонност към абстрактно мислене, естествено заемат водеща позиция в зората на математиката.
Развитието на математиката в Индия започва с митичен период. Според традицията най-ранните паметници на индийската математическа култура са религиозните книги: сутри и веди. Произходът им се приписва на VIII-VII век пр.н.е. В тях се излагат геометрични конструкции, които съставляват важна част от ритуалните условия за изграждане на религиозните сгради: храмове, олтари и други, и следователно в тях могат да се намерят първите начини за определяне на квадратурата на кръга и приложението на теоремата на Питагор. Очевидно в резултат на архитектурни изисквания е решен и аритметичният проблем за намиране на питагорейските тройки на естествените числа.
Числовата система се определя като десетична от древни времена. Санскритът е индоевропейски език, подобен на индоевропейските езици в Европа (за сравнение: 1 - ека, 2 - дви, 3 - три). В имената на числата се използва както адитивният, така и субстрактивният принцип. Например 19 би могло да бъде наречено едновременно „навадаша“ (девет и десет) и „екауна“ (без едно двадесет).
От древни времена е и склонността на индийците да работят с големи числа, което се отразява в легендите. Буда например е имал феноменална способност да брои и е дал числови наименования на всеки числов разред до 1054. Кандидатите за ръката на красивата богиня на Земята трябвало да се състезават в писане, аритметика, борба и стрелба с лък. Победителят в състезанието, Сарватасида, изобретява числова скала в геометрична прогрессия със знаменател 100, която нараства до число с 421 нули. Пристрастяването към операции с големи числа се запазва през цялата история на математиката в Индия.
Едни от първите числени знаци, използвани в Индия, са цифрите карощи, които в много отношения са подобни на финикийските и се изписват отдясно наляво. Те по-късно са заменени със знаците брахми, които се пишат отляво надясно като индийската писменост.
Наред с цифровия запис на числата е било широко използвано в Индия и словесно обозначаване, улеснено от богатия на синоними санскритски език. В този случай нулата се е обозначавала с думите "празно", "небе", "дупка"; единица - с имената на обекти, които съществуват само в единствено число: Луна, Земя; две - с думите "близнаци", "очи", "ноздри", "устни", "криле"; четири - думите "океани", "посоки на света" и т.н.
Около 500 г. сл. н. е. неизвестен индийски математик изобретява нова система за писане на числа - десетичната позиционна система. В него извършването на аритметични операции се оказва неизмеримо по-лесно, отколкото в старите, с неудобни буквени кодове, които използват гърците, или шейсетичните като при вавилонците. Впоследствие индийците използват сметала, адаптирани към позиционната система. Те разработват пълни алгоритми за всички аритметични операции, включително извличане на квадратни и кубични корени.
Позиционният принцип се употребява и при словесната номерация, при което една и съща дума, в зависимост от мястото, има различна числена стойност, а имената на разреда се пропускат.
Например числото 1021 може да се запише с думите "Луна - дупка - крила - Луна". Едно от имената за нула - "shunya" (празно) по-късно става основно. Когато през VIII век. индийските математически книги се превеждат на арабски, думата „шуня“ е преведена на арабската дума „syfr“, която има същото значение. Думата "syfr" в превода от арабските книги на латински остава без превод под формата на ciffra, откъдето идва френското и английското име за нула zero, немската дума Ziffer и нашата дума за "цифра", която първоначално е означавала нула.
Цифрите "брахми". От тези индийски знаци произхождат съвременните цифри.
На основата на числата на брахми са разработени съвременните индийски числа „Деванагари“ (божествена писменост), които се използват в десетичната позиционна система, от която произхождат десетичните позиционни системи на арабите и европейците. Ние наричаме измислените от индийците числа 1, 2, .., 9 и нула арабски, тъй като сме ги заели от арабите, но самите араби наричат тези числа индийски, а аритметиката, базирана на десетичната система - „индийско смятане“ (Hisab al-Hind).
Индийците наричат неизвестната стойност „яват-тават“ (толкова колкото), като буквата, означаваща сричката „я“, служи за обозначаване на неизвестното. Ако има няколко неизвестни, тогава те се наричат с думи, изразяващи различни цветове: калака (черно), пилака (синьо), питака (жълто), панда (бяло), лохита (червено) и се обозначават с първите срички на съответните думи: ка, ни, пи, да, ло. Свободният член в уравненията се придружава от първата сричка на думата "руна" (цяло). Понякога неизвестното се е обозначавало с нула, тъй като първоначално в таблиците, например за пропорционални стойности, за него се оставяла празна клетка.
Индийските математици, започвайки с Брахмагупта (7 век сл. н. е.), систематично използват отрицателни числа и третират положително число като собственост, а отрицателно число като дълг. Брахмагупта дава всички правила за аритметични операции с отрицателни числа. „Квадратът на положителните или отрицателните числа са положителни, техните квадратни корени ще бъдат съответно положителни и отрицателен. Тъй като отрицателното число по своята същност не е квадрат, то няма квадратен корен", пише през 850 г. Магавира в книгата си „Ганита-сара-санграха“ („Кратък курс по математика“).
Геометричните доказателства са изключително лаконични, но често много визуални. И така, за да се обоснове правилото за изчисляване на площта на триъгълник, е дадена фигура, в която височината на правоъгълника е равна на половината от височината на триъгълника (Вижте схемата по-долу).
За да обоснове предположението „Площта на кръг е равна на площта на правоъгълник, чиито страни са съответно равни на полукръга и радиуса", Ганеша (XVI век) разделя кръга на 12 равни сектора и след това разгръща всеки полукръг, състоящ се от 6 сектора, във фигура във форма на трион, чиято основа е равна на полукръга, а височината е равна на радиуса. Правоъгълникът, посочен в условието, ще бъде получен чрез вмъкване на зъбите на едния от "трионите" в процепите между зъбите на другия. Очевидно читателят е трябвало да си представи, че кръгът не е разделен на 12, а на толкова голям брой сектори, че тези сектори ще станат неразличими от триъгълниците, съставляващи „триона“.
 |
 |
Трябва да приемем, че дължим тези грандиозни изобретения не само на моментното просветление на някакъв случаен гений, който е изпреварил времето си, а че по същество е продукт на социалната среда и че тези изобретения отговарят на жизненоважни нужди на своето време.
От ранните математически трудове на санскрит изглежда ясно, че такава необходимост е съществувала, тъй като тези книги обсъждат много въпроси, засягащи търговията и социалните отношения и свързани със сложни изчисления.
Има проблеми по отношение на данъчното облагане, кредита и лихвите; проблеми на търговските обединения, борсовата търговия, както и обмена на монети и определянето на златното съдържание в пробите. Обществото става сложно и много хора са заети с административни функции и търговия.
Това е било невъзможно да се направи без прости методи за изчисление.
Приемането в Индия на нулата и десетичната позиционна бройна система дава простор на мисълта за бърз напредък в аритметиката и алгебрата, отбелязан в поредица открития: въвеждането на дробите, умножаване и делене на дроби; въвеждането и усъвършенстването на тройното правило; квадрати и кубове, квадратни корени кубични корени, както и символите им; знак минус; изчисляване на стойността на π на 3.1416; използване на букви от азбуката в алгебрата за обозначаване на неизвестни величини; използване на прости и квадратни уравнения; изследване на свойствата на нулата. Нашите термини „корен“ и „синус“ също ни напомнят за ролята на индийските учени в развитието на алгебрата и тригонометрията.
Въпросите
През 19 век германският математик Леополд Кронекер казва „Бог е направил целите числа, всичко останало е дело на човека“.
"Съгласен съм с това чувство, поне за положителните цели числа - целите числа, с които броим, - защото вавилонците не са вярвали в нулата или отрицателните числа", пише Даниел Мансфийлд.
Математиката се случва от много, много отдавна. Много преди древна Гърция и Питагор.
Дали е реална? За повечето култури само някои неща като положителните числа и правоъгълния триъгълник 3-4-5. Почти всичко останало в математиката се определя от обществото.
Източник:
The Conversation. Прочетете оригиналната статия.
Математика в Древней Индии, MaxBooks.Ru
НАУЧНОЕ НАСЛЕДИЕ ДРЕВНЕЙ ИНДИИ, «История и археология», Клопыжникова А.А., Ромах Н.И.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари