Възможно ли е извънземните да имат други представи за понятия като безкрайност, време и математика? На този въпрос се опитва да отговори математикът и програмист Робърт Уокър (Robert Walker) на страниците на quora.com.
Съвременната "земна" математика се е откъснала от практиката
В областите на математиката, свързани с множествата, е пълно с парадокси: парадокс на Ръсел, различни парадокси на Кантор, парадокс на Банах - Тарски, които според мнението на мнозина, са решени. Разбира се, в известен смисъл, нашата математиката е изящна и ако се следват правилата, не се получават противоречия. Но ако се вгледате в същите правила от независима философска гледна точка, математиката може да се тълкува по съвсем различен начин.
В математическия апарат има безкрайни величини, които са необходими на математиците предимно с цел да не се нарушава логиката. Много математици като Лютцен Брауер (Luitzen Egbertus Jan Brouwer), смятат, че трябва да остане само понятието за потенциална безкрайност, а Дейвид ван Данциг задава въпроса дали да не се нарече числото 10 1010 безкрайно. Един математик от друга планета може да даде своя интерпретация на нашите теореми и да стигне до същите заключения.
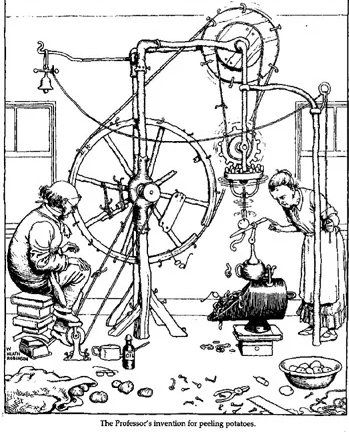Ето как Робърт Уокър илюстрира положението в съвременната математика: "Гениална, може би, красива, ако ви харесват такива неща - но защо е целият този труд само, за да се белят картофи?
Извънземните може просто да не си задават същите въпроси като нас или да имат различна от тази на земните математици гледна точка
Ето как Робърт Уокър определя евентуалните възможности пред извънземните математици:
- Извънземните биха могли да следват обичайния подход на земните математици;
- Или да имат различни възгледи за безкрайността от нас - може да са много по-практични по-"конструктивни" в подхода си към математиката, например, може въпросите за безкрайните величини въобще не възникват у тях.
- Или да са пренаписали цялата ни математика по някакъв сложен абстрактен начин, в която парадоксът на Скулем за тях да не е никакъв парадокс, а просто начин на математическо мислене?
- Или тези въпроси просто не възникват у тях по някаква друга причина или имат някакво друго значение за тях.
- Или, също като нас, има много гледни точки по тази тема? Един безкраен философски дебат, който продължава милиони години?
- А може да имат съвсем друг поглед по целия въпрос, непостижим за нас?
Варианти
Възможно е, основите на "земната" математика да са универсални и другите цивилизации също да разчитат на тях, но основите могат да бъдат и други: по-практични (без безкрайни величини) или по-абстрактни, а може и да използват много по-различна логика, за която не сме се сетили. Може би извънземните математици са намерили по-елегантни начини за решение на проблемите, а може тяхната математика да е още по-тромава от нашата. Историята на математиката показва, че много от идеите, които сега за нас изглеждат очевидни, са били незабелязани в продължение на векове. Да не говорим, че днес в училище се учи това, което преди няколко века са разбирали единици.
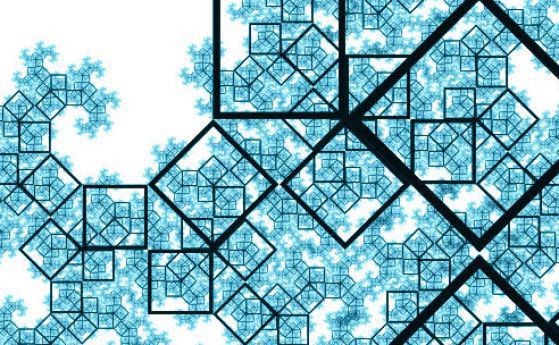
Не е изключено, извънземните да използват активно многозначна (паранепротиворечива) логика. Противоречията може да не ги притесняват така, както нас: те могат да тръгнат от това, че е доказуемо както потвърждението, така и отрицанието, което не допуска класическата логика.
Или може би вече има земни математици, които са измислили моделите, използвани от извънземните, например, Абрахам Робинсън и Пьотр Вопенка, които улесняват възприемането на безкрайно малките и големи величини.
А може би основите на нашата математика са плод на обстоятелствата. Ако следвахме подхода на изчисляване не на Нютон, а на Лайбниц, предпочитащ да работи с по-конкретни стойности, нещата щяха да се развият по друг начин.
Времето
Друг възможен сценарий е извънземните да не възприемат времето като линейно. Може да са отхвърлили идеята за миналото: да не им трябва да помнят кога, а къде е имало някакво събитие. Така например, ако живеят някъде под ледената покривка на спътника на Юпитер, Европа, те не биха могли да наблюдават смяната на сезоните.
Има вариант да използват понятието за линейно време, но да го възприемат по-скоро в рамките на квантовата механика като няколко състояния едновременно. Може да не следват нашата евклидова геометрия или да са се отказали да изчисляват, игнорирайки изцяло понятието за дискретни стойности, предпочитайки да мислят с множества.
Други възможни подходи:
- фрактална математика, когато светът се описва само с фрактали - множества, еднородни в различни мащаби на измерване;
- комбинаторна геометрия (множества или структури от еднотипни геометрични обекти);
- отказ от числата въобще или аритметични операции с тях;
- отхвърляне на математиката като начин да се описва реалността, както и точните науки по принцип (аналогов и хуманитарен подход към всичко).
"Мисля, че извънземната математика толкова може да се различава от нашата, че няма да можем да осъществим контакт веднага. Но не бих се изненадал, ако рано или късно намерим някакви паралели между нашите и техните математически модели. И след това няма да е трудно да се измисли единна система, която да е ясна за всички, без изключение, разумни организми." - заключава Робърт Уокър.
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
06.09 2015 в 20:01
06.09 2015 в 08:56
Дали на един физик и един математик да решат две задачи.
Задача 1. Имаме чешма, празен чайник и котлон. Как да сварим вода?
И двамата участници предложили един и същ отговор:
Напълваме чайника с вода от чешмата, слагаме го на котлона и сваряваме водата.
Задача 2. Имаме чешма, пълен с вода чайник и котлон. Как да сварим вода?
Физикът дал следното решение:
Слагаме чайника на котлона и сваряваме водата.
Математикът предложил друго решение:
Изливаме водата от чайника и след това се намираме в условията на Задача 1, за която вече имаме готово решение.
Последни коментари