

–£ –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Α―²–Α –Η –Β―¹―²–Β―¹―²–≤–Β–Ϋ–Η―²–Β –Ϋ–Α―É–Κ–Η ―΅–Β―¹―²–Ψ ―¹–Β –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α―² –≥―Ä―É–Ω–Η –Ζ–Α –Ψ―²–Κ―Ä–Η–≤–Α–Ϋ–Β –Ϋ–Α –≤―ä―²―Ä–Β―à–Ϋ–Α―²–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α –Ψ–±–Β–Κ―²–Η―²–Β.¬†–£―ä―²―Ä–Β―à–Ϋ–Α―²–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ψ ―¹–Β ―¹–≤―ä―Ä–Ζ–≤–Α ―¹ –Η–Ϋ–≤–Α―Ä–Η–Α–Ϋ―²–Ϋ–Ψ―¹―² –Η–Μ–Η –Φ–Ϋ–Ψ–Ε–Β―¹―²–≤–Ψ―²–Ψ –Ω―Ä–Β–Ψ–±―Ä–Α–Ζ–Ψ–≤–Α–Ϋ–Η―è, –Κ–Ψ–Η―²–Ψ –Ζ–Α–Ω–Α–Ζ–≤–Α―² ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α, –Ζ–Α–Β–¥–Ϋ–Ψ ―¹ –Ψ–Ω–Β―Ä–Α―Ü–Η―è―²–Α –Κ–Ψ–Φ–Ω–Ψ–Ζ–Η―Ü–Η―è –Η–Μ–Η ―¹―É–Ω–Β―Ä–Ω–Ψ–Ζ–Η―Ü–Η―è (–Ϋ–Α―¹–Μ–Α–≥–≤–Α–Ϋ–Β –Ϋ–Α –¥–≤–Β –Ψ–Ω–Β―Ä–Α―Ü–Η–Η - ―É―¹–Μ–Ψ–≤–Ϋ–Ψ―²–Ψ –¥–Β–Ι―¹―²–≤–Η–Β "―É–Φ–Ϋ–Ψ–Ε–Β–Ϋ–Η–Β" βÄΔ ), –Ψ–±―Ä–Α–Ζ―É–≤–Α―² –≥―Ä―É–Ω–Α, –Ϋ–Α―Ä–Β―΅–Β–Ϋ–Α –≥―Ä―É–Ω–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η–Η―²–Β.
–€–Α―²–Β–Φ–Α―²–Η―Ü–Η―²–Β ―¹–Α –≤―ä–≤–Β–Μ–Η –Β–¥–Ϋ–Α –Ϋ―É–Μ–Β–≤–Α –Ψ–Ω–Β―Ä–Α―Ü–Η―è –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –Κ–Ψ―è―²–Ψ –Β –Ϋ–Α―Ä–Β―΅–Β–Ϋ–Α¬†–Ψ–Ω–Β―Ä–Α―Ü–Η―è –Ϋ–Α –Η–¥–Β–Ϋ―²–Η―΅–Ϋ–Ψ―¹―², –Κ–Ψ―è―²–Ψ –Ϋ–Β –Η–Ζ–Φ–Β–Ϋ―è –Ω–Ψ–Μ–Ψ–Ε–Β–Ϋ–Η–Β―²–Ψ –Ϋ–Α –Ψ–±–Β–Κ―²–Η―²–Β, –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α–Ϋ–Α ―¹¬†–ï. –ù–Β–Ψ–±―Ö–Ψ–¥–Η–Φ–Α –Β –Κ–Α―²–Ψ –Β–¥–Η–Ϋ–Η―΅–Β–Ϋ –Β–Μ–Β–Φ–Β–Ϋ―² –Ζ–Α –¥–Α –¥–Ψ–Ω―ä–Μ–Ϋ–Η –≥―Ä―É–Ω–Η―²–Β –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –Ω–Ψ–¥–Ψ–±–Ϋ–Ψ –Ϋ–Α ―΅–Η―¹–Μ–Ψ―²–Ψ 0 –Ω―Ä–Η ―¹―ä–±–Η―Ä–Α–Ϋ–Β―²–Ψ –Η–Μ–Η –Β–¥–Η–Ϋ–Η―Ü–Α―²–Α –Ω―Ä–Η ―É–Φ–Ϋ–Ψ–Ε–Β–Ϋ–Η–Β―²–Ψ.
–û–≥–Μ–Β–¥–Α–Μ–Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è
| –™―Ä―É–Ω–Α―²–Α –Ϋ–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Α―²–Α ―¹–Η–Φ–Β―²―Ä–Η―è ―¹–Β ―¹―ä―¹―²–Ψ–Η –Ψ―² –¥–≤–Α –Β–Μ–Β–Φ–Β–Ϋ―²–Α: –Ψ–Ω–Β―Ä–Α―Ü–Η―è―²–Α –Ζ–Α –Η–¥–Β–Ϋ―²–Η―΅–Ϋ–Ψ―¹―² –Η–Ζ–Ω―ä–Μ–Ϋ―è–≤–Α ―Ä–Ψ–Μ―è―²–Α –Ϋ–Α¬†–Β–¥–Η–Ϋ–Η―΅–Β–Ϋ –Β–Μ–Β–Φ–Β–Ϋ―²¬†–≤ –≥―Ä―É–Ω–Α―²–Α, –Α –≤―¹―è–Κ–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Α –Ψ–Ω–Β―Ä–Α―Ü–Η―è (M) –Η–Φ–Α ―¹–≤–Ψ―è –Ψ–±―Ä–Α―²–Ϋ–Α, –Κ–Ψ―è―²–Ψ –Η–Ζ–Ω―ä–Μ–Ϋ–Β–Ϋ–Α ―¹–Μ–Β–¥ –Ϋ–Β―è –¥–Ψ–≤–Β–Ε–¥–Α –¥–Ψ –Ψ―Ä–Η–≥–Η–Ϋ–Α–Μ–Ϋ–Η―è –≤–Η–¥ –Ϋ–Α –Ψ–±–Β–Κ―²–Α. |
|
–û–≥–Μ–Β–¥–Α–Μ–Ϋ–Α―²–Α ―¹–Η–Φ–Β―²―Ä–Η―è¬†–Β –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η ―¹–≤―ä―Ä–Ζ–Α–Ϋ–Α ―¹ –≥―Ä―É–Ω–Α―²–Α SO (1).
–‰–Ϋ–≤–Β―Ä―¹–Η―è
|
–™―Ä―É–Ω–Α―²–Α –Ϋ–Α –Η–Ϋ–≤–Β―Ä―¹–Η―è―²–Α ―¹―ä―â–Ψ ―¹–Β ―¹―ä―¹―²–Ψ–Η –Ψ―² –¥–≤–Α –Β–Μ–Β–Φ–Β–Ϋ―²–Α: ¬†–Β–¥–Η–Ϋ–Η―΅–Ϋ–Η―è –Β–Μ–Β–Φ–Β–Ϋ―²¬†E –Η –Ψ–Ω–Β―Ä–Α―Ü–Η―è―²–Α –Η–Ϋ–≤–Β―Ä―¹–Η―è, –Κ–Ψ―è―²–Ψ –Η–Ζ–Ω―ä–Μ–Ϋ–Β–Ϋ–Α –¥–≤–Α –Ω―ä―²–Η –¥–Α–≤–Α –Ψ―Ä–Η–≥–Η–Ϋ–Α–Μ–Ϋ–Η―è –Ψ–±–Β–Κ―². –Δ–Α–Ζ–Η –≥―Ä―É–Ω–Α –Β –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Ϋ–Α (―²―ä–Ε–¥–Β―¹―²–≤–Β–Ϋ–Α) –Ϋ–Α –≥―Ä―É–Ω–Α―²–Α –Ϋ–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Α―²–Α ―¹–Η–Φ–Β―²―Ä–Η―è. |
|
–½–Α–≤―ä―Ä―²–Α–Ϋ–Β –Ϋ–Α 180¬Α (C2, ―Ü–Β–Ϋ―²―Ä–Α–Μ–Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è)
| –™―Ä―É–Ω–Α ―¹–Α –Η –¥–≤–Β –Ζ–Α–≤―ä―Ä―²–Α–Ϋ–Η―è –Ϋ–Α 0¬Α –Η 180¬Α –Ψ–Κ–Ψ–Μ–Ψ –Β–¥–Ϋ–Α –Ψ―¹, –Α–Κ–Ψ –Ζ–Α –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Ψ―² –¥–≤–Β –Ζ–Α–≤―ä―Ä―²–Α–Ϋ–Η―è ―¹–Β ―¹–Φ―è―²–Α –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ–Ϋ–Ψ―²–Ψ –Η–Φ –Η–Ζ–Ω―ä–Μ–Ϋ–Β–Ϋ–Η–Β. –Δ–Ψ–≤–Α –Β –≥―Ä―É–Ω–Α C2. –Δ―è –Β –Η–Ζ–Ψ–Φ–Ψ―Ä―³–Ϋ–Α –Ϋ–Α –≥–Ψ―Ä–Ϋ–Η―²–Β –¥–≤–Β –≥―Ä―É–Ω–Η. –½–Α–≤―ä―Ä―²–Α–Ϋ–Β―²–Ψ –Ϋ–Α ―ä–≥―ä–Μ 0¬Α –Β –Η–¥–Β–Ϋ―²–Η―΅–Ϋ–Ψ ―¹ –Β–¥–Η–Ϋ–Η―΅–Ϋ–Η―è –Β–Μ–Β–Φ–Β–Ϋ―² E. |
|
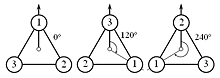
–™―Ä―É–Ω–Α C3
|
–ü–Ψ –Α–Ϋ–Α–Μ–Ψ–≥–Η―è ―¹ –≥―Ä―É–Ω–Α C2¬†–Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ω–Ψ―¹―²―Ä–Ψ–Η –≥―Ä―É–Ω–Α¬†C3, ―¹―ä―¹―²–Ψ―è―â–Α ―¹–Β –Ψ―² –Ζ–Α–≤―ä―Ä―²–Α–Ϋ–Η―è –Ϋ–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α―²–Α –Ϋ–Α ―ä–≥―ä–Μ 0¬Α, 120¬Α –Η 240¬Α. –û―² ―²–Α–±–Μ–Η―Ü–Α―²–Α ―¹–Β –≤–Η–Ε–¥–Α, ―΅–Β –Α–Κ–Ψ –Ζ–Α–≤―ä―Ä―²–Η–Φ –Ω―Ä–Α–≤–Η–Μ–Ϋ–Η―è ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ–Ϋ–Ψ –Ϋ–Α 120¬Α –Η 240¬Α (–Ψ–±―â–Ψ 360¬Α), –Ω–Ψ–Μ―É―΅–Α–≤–Α–Φ–Β E, ―².–Β. –Ψ―Ä–Η–≥–Η–Ϋ–Α–Μ–Ϋ–Η―è –≤–Η–¥ –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α. –™―Ä―É–Ω–Α―²–Α –Β –Α–±–Β–Μ–Β–≤–Α: R120βÄΔ R240 = R240 βÄΔ R120 =E |
 |
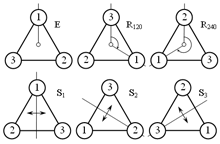
–î–Η–Β–¥―Ä–Α–Μ–Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è
|
–Δ–Α–±–Μ–Η―Ü–Α―²–Α –Ϋ–Α –ö–Β–Ι–Μ–Η –≤–¥―è―¹–Ϋ–Ψ¬†–Ω–Ψ–Κ–Α–Ζ–≤–Α –¥–Η–Β–¥―Ä–Α–Μ–Ϋ–Α―²–Α –≥―Ä―É–Ω–Α D3¬†, –Ψ–±–Β–¥–Η–Ϋ–Η–Μ–Α –≤―¹–Η―΅–Κ–Η ―¹–Η–Φ–Β―²―Ä–Η–Η –Ϋ–Α¬†―Ä–Α–≤–Ϋ–Ψ―¹―²―Ä–Α–Ϋ–Β–Ϋ ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ. –ê–Κ–Ψ –¥–Ψ–±–Α–≤–Η–Φ –Κ―ä–Φ –≥―Ä―É–Ω–Α―²–Α C3 –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Η –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η―è –Ϋ–Α ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α –Ω–Ψ ―²―Ä–Η―²–Β –Ψ―¹–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è (S1, S2, S3), ―â–Β –Ω–Ψ–Μ―É―΅–Η–Φ –Ω―ä–Μ–Β–Ϋ –Ϋ–Α–±–Ψ―Ä –Ψ―² –Ψ–Ω–Β―Ä–Α―Ü–Η–Η, –Κ–Ψ–Η―²–Ψ ―²―Ä–Α–Ϋ―¹―³–Ψ―Ä–Φ–Η―Ä–Α―² ―²―Ä–Η―ä–≥―ä–Μ–Ϋ–Η–Κ–Α –≤ ―¹–Α–Φ–Η―è ―¹–Β–±–Β ―¹–Η. –ê–Κ–Ψ –Η–Ζ–Ω―ä–Μ–Ϋ–Η–Φ –Ω–Ψ―¹–Μ–Β–¥–Ψ–≤–Α―²–Β–Μ–Ϋ–Ψ –¥–≤–Β –Η–¥–Β–Ϋ―²–Η―΅–Ϋ–Η –Ψ–Ω–Β―Ä–Α―Ü–Η–Η –Ϋ–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –Ω–Ψ–Μ―É―΅–Α–≤–Α–Φ–Β E. –ö–Ψ–Φ―É―²–Α―²–Η–≤–Ϋ–Η―è―² –Ζ–Α–Κ–Ψ–Ϋ –Ϋ–Β –≤–Α–Ε–Η - –≥―Ä―É–Ω–Α―²–Α –Ϋ–Β –Β –Α–±–Β–Μ–Β–≤–Α. –ù–Α–Ω―Ä–Η–Φ–Β―Ä: S1βÄΔ S2 =R240 β↠S2βÄΔ S1 =R120 ¬† |
 |
–ë―Ä–Ψ―è―² –Ϋ–Α –Ψ–Ω–Β―Ä–Α―Ü–Η–Η―²–Β, –Ψ–±―Ä–Α–Ζ―É–≤–Α―â–Η –≥―Ä―É–Ω–Α―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, ―¹–Β –Ϋ–Α―Ä–Η―΅–Α –Ω–Ψ―Ä―è–¥―ä–Κ –Ϋ–Α –≥―Ä―É–Ω–Α―²–Α.
–ï–¥–Ϋ–Ψ ―²―è–Μ–Ψ(―³–Η–≥―É―Ä–Α) –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ψ–Ω–Η―à–Β ―¹ –Ω–Ψ–Φ–Ψ―â―²–Α –Ϋ–Α ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Η –≥―Ä―É–Ω–Η ―¹–Η–Φ–Β―²―Ä–Η―è. –û―¹–Ϋ–Ψ–≤–Ϋ–Η―²–Β –≥―Ä―É–Ω–Η ―¹–Α:
- –Δ–Ψ―΅–Κ–Ψ–≤–Η –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è - 32 . –û–±–Β–¥–Η–Ϋ―è–≤–Α―² ―²–Α–Κ–Η–≤–Α ―¹–Η–Φ–Β―²―Ä–Η―΅–Ϋ–Η –Ψ–Ω–Β―Ä–Α―Ü–Η–Η, –Ω―Ä–Η –Κ–Ψ–Η―²–Ψ –Ψ―¹―²–Α–≤–Α –Ω–Ψ–Ϋ–Β –Β–¥–Ϋ–Α –Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Ϋ–Α ―²–Ψ―΅–Κ–Α. –û–±―Ä–Α–Ζ―É–≤–Α―² ―¹–Β –Ψ―² –≤–Ζ–Α–Η–Φ–Ψ–¥–Β–Ι―¹―²–≤–Η―è―²–Α –Ϋ–Α –Ω―Ä–Ψ―¹―²–Η –Β–Μ–Β–Φ–Β–Ϋ―²–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è - ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Η –Ψ―¹–Η. –û–Ω–Η―¹–≤–Α―² –≤―ä–Ϋ―à–Ϋ–Α―²–Α ―³–Ψ―Ä–Φ–Α –Ϋ–Α ―²–Β–Μ–Α―²–Α;.
- –™―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –≤ –¥–≤―É–Φ–Β―Ä–Ϋ–Ψ―²–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ - 17.¬†–Δ–Ψ–≤–Α ―¹–Α ―³–Η–≥―É―Ä–Η, –Κ–Ψ–Η―²–Ψ –Ζ–Α–Ω―ä–Μ–≤–Α―² –Ω–Μ―ä―²–Ϋ–Ψ ―Ä–Α–≤–Ϋ–Η–Ϋ–Α―²–Α, –Ϋ–Α―Ä–Η―΅–Α–Ϋ–Η ―¹–Α –Ω–Α―²–Β―Ä–Ϋ–Η, –Φ–Ψ–Ε–Β –Η –Ϋ–Α –±―ä–Μ–≥–Α―Ä―¹–Κ–Η: –Φ–Ψ–Ζ–Α–Ι–Κ–Η, ―²–Α–Ω–Β―²–Η. –£―¹–Η―΅–Κ–Η –Φ–Ψ–Ζ–Α–Ι–Κ–Η, –Κ–Ψ–Η―²–Ψ –Φ–Ψ–≥–Α―² –¥–Α –Η–Ζ–Ω―ä–Μ–Ϋ―è―² ―Ä–Α–≤–Ϋ–Η–Ϋ–Α ―¹ –Ω–Ψ–≤―²–Α―Ä―è―â–Η ―¹–Β ―³–Η–≥―É―Ä–Η, –Ω―Ä–Η–Ϋ–Α–¥–Μ–Β–Ε–Α―² –Ϋ–Α –Β–¥–Ϋ–Α –Ψ―² 17-―²–Β –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Κ–Α―²–Ψ –Β–Μ–Β–Φ–Β–Ϋ―²–Η―²–Β –Ϋ–Α ―²–Β–Ζ–Η –≥―Ä―É–Ω–Η –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–≤–Α―² ―¹–Α–Φ–Ψ ―²―Ä–Α–Ϋ―¹–Μ–Α―Ü–Η―è, ―Ä–Ψ―²–Α―Ü–Η―è –Η –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Ψ –Ψ―²―Ä–Α–Ζ―è–≤–Α–Ϋ–Β, –Η–Ζ–Ω―ä–Μ–Ϋ–Β–Ϋ–Η –≤ –Κ–Ψ–Φ–±–Η–Ϋ–Α―Ü–Η―è –≤―ä―Ä―Ö―É –Β–¥–Η–Ϋ –Ψ―¹–Ϋ–Ψ–≤–Β–Ϋ –Φ–Ψ―²–Η–≤. –ü―ä–Μ–Β–Ϋ ―¹–Ω–Η―¹―ä–Κ –Ϋ–Α –≤―¹–Η―΅–Κ–Η ―¹–Β–¥–Β–Φ–Ϋ–Α–¥–Β―¹–Β―² –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Η –≥―Ä―É–Ω–Η - –Ψ―² de.wikipedia
- –ü―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Η –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è - –Ψ–±―â–Ψ 230. –û–±―Ä–Α–Ζ―É–≤–Α ―¹–Β –Ψ―² –≤–Ζ–Α–Η–Φ–Ψ–¥–Β–Ι―¹―²–≤–Η–Β―²–Ψ –Ϋ–Α –≤―¹–Η―΅–Κ–Η –Β–Μ–Β–Φ–Β–Ϋ―²–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è (―Ä–Α–≤–Ϋ–Η–Ϋ–Η, –Ψ―¹–Η, ―²―Ä–Α–Ϋ―¹–Μ–Α―Ü–Η–Η –Η ―Ä–Β―à–Β―²–Κ–Η). –û–Ω–Η―¹–≤–Α―² –Ϋ–Β ―¹–Α–Φ–Ψ –≤―ä–Ϋ―à–Ϋ–Η―è –≤–Η–¥, –Ϋ–Ψ –Η –≤―ä―²―Ä–Β―à–Ϋ–Α―²–Α ―¹―²―Ä―É–Κ―²―É―Ä–Α, –Ϋ–Α–Ω―Ä–Η–Φ–Β―Ä –Α―²–Ψ–Φ–Ϋ–Α―²–Α ―¹―²―Ä―É–Κ―²―É―Ä–Α –Ϋ–Α –Κ―Ä–Η―¹―²–Α–Μ–Η―²–Β;
- –ü―Ä–Β–¥–Β–Μ–Ϋ–Η –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è - 7
–ö–Ψ–≥–Α―²–Ψ –Η–Φ–Α–Φ–Β –¥–≤–Β –Η–Μ–Η –Ω–Ψ–≤–Β―΅–Β ―³–Η–≥―É―Ä–Η ―¹ ―Ä–Α–Ζ–Μ–Η―΅–Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η –≥–Η –Ϋ–Α–Μ–Ψ–Ε–Η–Φ –Ω–Ψ –Ϋ―è–Κ–Α–Κ―ä–≤ –Ϋ–Α―΅–Η–Ϋ, ―²–Α–Κ–Α ―΅–Β –¥–Α –Ω–Ψ–Μ―É―΅–Η–Φ –Ϋ–Ψ–≤–Α ―³–Η–≥―É―Ä–Α, ―²–Ψ ―¹–Β –Ω–Ψ–Μ―É―΅–Α–≤–Α –Ϋ–Ψ–≤–Α –≥―Ä―É–Ω–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –Κ–Ψ―è―²–Ψ ―¹–Β ―è–≤―è–≤–Α –Ω–Ψ–¥–≥―Ä―É–Ω–Α –Ϋ–Α ―²–Β–Ζ–Η –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α ―²–Β–Μ–Α―²–Α, –Ψ―² –Κ–Ψ–Η―²–Ψ –Β ―¹―ä―¹―²–Α–≤–Ϋ–Α―²–Α ―³–Η–≥―É―Ä–Α.
–‰–Φ–Α –Ω–Ψ–Ϋ–Β –¥–≤–Β –Φ–Β–Ε–¥―É–Ϋ–Α―Ä–Ψ–¥–Ϋ–Ψ –Ω―Ä–Η–Ζ–Ϋ–Α―²–Η ―¹–Η―¹―²–Β–Φ–Η –Ζ–Α –Ψ–±–Ψ–Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α ―²–Β–Μ–Α―²–Α, –Η–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Ϋ–Η –Ϋ–Α–Ι-–≤–Β―΅–Β –≤ –Κ―Ä–Η―¹―²–Α–Μ–Ψ–≥―Ä–Α―³–Η―è―²–Α - –®–Β–Ϋ―³–Μ–Η―¹ –Η –Ξ–Β―Ä–Φ–Α–Ϋ-–€–Ψ–≥–Β–Ϋ . –ü―Ä–Η–Μ–Α–≥–Α–Φ ―²–Α–±–Μ–Η―Ü–Α –Ζ–Α –Ψ–Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―΅–Ϋ–Η―²–Β ―²―Ä–Α–Ϋ―¹―³–Ψ―Ä–Φ–Α―Ü–Η–Η –Η –Ω–Ψ –¥–≤–Β―²–Β ―¹–Η―¹―²–Β–Φ–Η:
|
–û–±–Ψ–Ζ–Ϋ–Α―΅–Β–Ϋ–Η―è –Ω–Ψ | –Δ―Ä–Α–Ϋ―¹―³–Ψ―Ä–Φ–Α―Ü–Η―è | |
|---|---|---|
|
–®–Β–Ϋ―³–Μ–Η―¹ |
–Ξ–Β―Ä–Φ–Α–Ϋ-–€–Ψ–≥–Β–Ϋ | |
| –ï | 1 |
–Δ―ä–Ε–¥–Β―¹―²–≤–Β–Ϋ–Ψ –Ω―Ä–Β–Ψ–±―Ä–Α–Ζ–Ψ–≤–Α–Ϋ–Η–Β –Ϋ–Α –Ψ–±–Β–Κ―²–Α |
| Cn | –Ω | –½–Α–≤―ä―Ä―²–Α–Ϋ–Β –Ϋ–Α ―ä–≥―ä–Μ 2œÄ/n. –Γ–Η–Φ–Β―²―Ä–Η―è―²–Α –Β ―¹ –Ω–Ψ―Ä―è–¥―ä–Κ n , –Κ–Α―²–Ψ n –Β –Φ–Α–Κ―¹–Η–Φ–Α–Μ–Ϋ–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² –Ω―Ä–Η –Κ–Ψ―è―²–Ψ –Ω―Ä–Η –Ζ–Α–≤―ä―Ä―²–Α–Ϋ–Β 2œÄ/n –Ψ–±–Β–Κ―²―ä―² ―¹―ä–≤–Ω–Α–¥–Α ―¹―ä―¹ ―¹–Β–±–Β ―¹–Η ¬† |
| C'2, U2 | 2 | –½–Α–≤―ä―Ä―²–Α–Ϋ–Β –Ϋ–Α ―ä–≥―ä–Μ œÄ –Ψ–Κ–Ψ–Μ–Ψ –Ψ―¹ –Ψ―² –≤―²–Ψ―Ä–Η –Ω–Ψ―Ä―è–¥―ä–Κ, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α –Ϋ–Α –≥–Μ–Α–≤–Ϋ–Α―²–Α –Ψ―¹ |
| œÉh | 1/m | –û–≥–Μ–Β–¥–Α–Μ–Ϋ–Ψ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Β¬† –Ψ―²–Ϋ–Ψ―¹–Ϋ–Ψ¬† ―Ä–Α–≤–Ϋ–Η–Ϋ–Α, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α –Ϋ–Α –≥–Μ–Α–≤–Ϋ–Α―²–Α –Ψ―¹ |
| œÉv | m | –û–≥–Μ–Β–¥–Α–Μ–Ϋ–Ψ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Β¬† –Ψ―²–Ϋ–Ψ―¹–Ϋ–Ψ¬† ―Ä–Α–≤–Ϋ–Η–Ϋ–Α, ―¹―ä–¥―ä―Ä–Ε–Α―â–Α –≥–Μ–Α–≤–Ϋ–Α―²–Α –Ψ―¹ |
| œÉd | m | –û–≥–Μ–Β–¥–Α–Μ–Ϋ–Ψ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Β¬† –Ψ―²–Ϋ–Ψ―¹–Ϋ–Ψ¬† ―Ä–Α–≤–Ϋ–Η–Ϋ–Α, ―¹―ä–¥―ä―Ä–Ε–Α―â–Α –≥–Μ–Α–≤–Ϋ–Α―²–Α –Ψ―¹ –Η –¥–Β–Μ―è―â–Α –Ω–Ψ―Ä–Α–≤–Ϋ–Ψ ―ä–≥―ä–Μ–Α –Φ–Β–Ε–¥―É –¥–≤–Β―²–Β –Ψ―¹–Η, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Η –Η–Μ–Η –Ϋ–Α–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η –Κ―ä–Φ –≥–Μ–Α–≤–Ϋ–Α―²–Α –Ψ―¹ |
| Sn | –Ω/m=n | –û–≥–Μ–Β–¥–Α–Μ–Ϋ–Ψ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Β¬† –Ψ―²–Ϋ–Ψ―¹–Ϋ–Ψ¬† ―Ä–Α–≤–Ϋ–Η–Ϋ–Α, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α –Ϋ–Α –Ψ―¹―²–Α –Ϋ–Α ―Ä–Ψ―²–Α―Ü–Η―è Cn |
| I=S2 | 2 | –‰–Ϋ–≤–Β―Ä―¹–Η―è –Ψ―²–Ϋ–Ψ―¹–Ϋ–Ψ –Ϋ–Α―΅–Α–Μ–Ψ―²–Ψ –Ϋ–Α –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²–Ϋ–Α―²–Α ―¹–Η―¹―²–Β–Φ–Α (―Ü–Β–Ϋ―²―ä―Ä–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è) |
–ü―Ä–Β–¥–Β–Μ–Ϋ–Η –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è
–ü–Ψ–Ϋ―è―²–Η–Β―²–Ψ "–Ω―Ä–Β–¥–Β–Μ–Ϋ–Η –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è" –Β –≤―ä–≤–Β–¥–Β–Ϋ–Ψ –≤ –Κ―Ä–Η―¹―²–Α–Μ–Ψ–≥―Ä–Α―³–Η―è―²–Α –Ζ–Α –Ψ–Ω–Η―¹–Α–Ϋ–Η–Β –Ϋ–Α ―³–Η–Ζ–Η―΅–Ϋ–Η―²–Β ―¹–≤–Ψ–Ι―¹―²–≤–Α –Ϋ–Α –Κ―Ä–Η―¹―²–Α–Μ–Η―²–Β. –Λ―Ä–Β–Ϋ―¹–Κ–Η―è―² ―³–Η–Ζ–Η–Κ –ü–Η–Β―Ä –ö―é―Ä–Η –Ω―Ä–Β–¥–Μ–Ψ–Ε–Η–Μ ―¹–Β–¥–Β–Φ ―²–Α–Κ–Η–≤–Α –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è: –Κ–Ψ–Ϋ―É―¹, ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä –Η ―¹―³–Β―Ä–Α.
–î―É–Φ–Α―²–Α "–Ω―Ä–Β–¥–Β–Μ–Ϋ–Η" –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α, ―΅–Β ―Ä–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Η―²–Β ―²–Β–Μ–Α –Φ–Ψ–≥–Α―² –¥–Α ―¹–Β ―Ä–Α–Ζ–≥–Μ–Β–Ε–¥–Α―² –Κ–Α―²–Ψ ―Ä–Β–Ζ―É–Μ―²–Α―² –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Ψ ―É–≤–Β–Μ–Η―΅–Β–Ϋ–Η–Β –Ϋ–Α –±―Ä–Ψ―è –Ϋ–Α ―¹―²―Ä–Α–Ϋ–Η―²–Β –Ϋ–Α –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ–Η:
- –Ψ―² –Ω–Η―Ä–Α–Φ–Η–¥–Α - –Κ–Ψ–Ϋ―É―¹,
- –Ψ―² –Ω―Ä–Η–Ζ–Φ–Α - ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä –Η
- –Ψ―² –Ψ–±–Β–Φ–Ϋ–Η –Φ–Ϋ–Ψ–≥–Ψ―¹―²–Β–Ϋ–Η –Κ–Α―²–Ψ –Κ―É–±, –Ψ–Κ―²–Α–Β–¥―ä―Ä, –¥–Ψ–¥–Β–Κ–Α–Β–¥―ä―Ä –Η –¥―Ä. - –Κ―ä–Μ–±–Ψ.
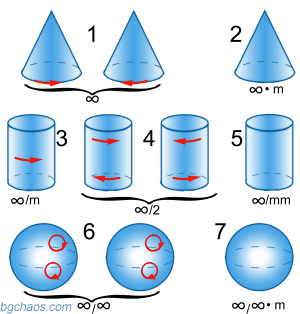 |
–½–Ϋ–Α―Ü–Η―²–Β –Ω–Ψ–¥ ―³–Η–≥―É―Ä–Η―²–Β ―¹–Α –Ψ―² ―¹–Η–Φ–≤–Ψ–Μ–Η–Κ–Α―²–Α –Ϋ–Α –Ξ–Β―Ä–Φ–Α–Ϋ-–€–Ψ–≥–Β–Ϋ (Hermann-Mauguin) –Ζ–Α –Ψ―²–±–Β–Μ―è–Ζ–≤–Α–Ϋ–Β –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α. –†–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Η―²–Β –Ψ―¹–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è ―¹–Β –Ω―Ä–Β–¥―¹―²–Α–≤―è―² ―¹ –Α―Ä–Α–±―¹–Κ–Η ―Ü–Η―³―Ä–Η - 1, 2, 3...n..., –≤ ―¹–Μ―É―΅–Α―è –Η –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Ψ―¹―² βàû –‰–Ϋ–≤–Β―Ä―¹–Η–Ψ–Ϋ–Ϋ–Η―²–Β –Ψ―¹–Η ―¹–Β –Ω―Ä–Β–¥―¹―²–Α–≤―è―² ―¹ –Α―Ä–Α–±―¹–Κ–Η ―Ü–Η―³―Ä–Η ―¹ –Μ–Η–Ϋ–Η–Η –Ψ―²–≥–Ψ―Ä–Β - n. –û―¹ 2 –Β –≤―¹―ä―â–Ϋ–Ψ―¹―² –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η ―¹–Β –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α ―¹ m (mirror). –ê–Κ–Ψ –Ϋ―è–Κ–Ψ―è –Ψ―² –Ψ―¹–Η―²–Β ―¹–Α –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Η –Ϋ–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Α―²–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α ―²―Ä―è–±–≤–Α –¥–Α ―¹–Μ–Ψ–Ε–Η–Φ ―΅–Β―Ä―²–Α (/) –Φ–Β–Ε–¥―É ―¹–Η–Φ–≤–Ψ–Μ–Α –Ϋ–Α –Ψ―¹―²–Α –Η ―¹–Η–Φ–≤–Ψ–Μ–Α –Ϋ–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Α―²–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α. –Δ―É–Κ βàû –Β ―Ä–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Α –Ψ―¹ –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ ―Ä–Β–¥, m - ―Ä–Α–≤–Ϋ–Η–Ϋ–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, 2 - ―Ä–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Α –Ψ―¹ –Ψ―² –≤―²–Ψ―Ä–Η ―Ä–Β–¥. –ù–Α–Ω―Ä–Η–Φ–Β―Ä –Ζ–Α–Ω–Η―¹―ä―² βàû m, –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α ―΅–Β –Η–Φ–Α ―Ä–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Α –Ψ―¹ –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ ―Ä–Β–¥ –Η –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –Φ–Η–Ϋ–Α–≤–Α―â–Η –Ω―Ä–Β–Ζ ―²–Α–Ζ–Η –Ψ―¹, –Α βàû/m - ―Ä–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Α –Ψ―¹ –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ ―Ä–Β–¥ –Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Α –Ϋ–Α ―²–Α–Ζ–Η –Ψ―¹ |
1.¬†–™―Ä―É–Ω–Α βàû, (–Β–¥–Ϋ–Α –Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ). –Δ―è ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Α –Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ–Φ–Β―Ä–Ϋ–Ψ –≤―ä―Ä―²―è―â ―¹–Β –Κ–Ψ–Ϋ―É―¹. –™―Ä―É–Ω–Α –Β –Ω–Ψ–Μ―è―Ä–Ϋ–Α –Η¬†–Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Α¬†(–Η–Μ–Η¬†―Ö–Η―Ä–Α–Μ–Ϋ–Α¬†βÄ™ ―Ö–Η―Ä–Α–Μ–Ϋ–Ψ―¹―²–Α –Β –Β–¥–Ϋ–Α –Ψ―² ―²―Ä―É–¥–Ϋ–Ψ―¹―²–Η―²–Β –Ω―Ä–Β–¥ –Α–±–Η–Ψ–≥–Β–Ϋ–Β–Ζ–Α―²–Α).
–ï–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Η―²–Β¬†―¹–Α –¥–≤–Ψ–Ι–Κ–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Ψ –Α―¹–Η–Φ–Β―²―Ä–Η―΅–Ϋ–Η –Ψ–±–Β–Κ―²–Η (―³–Η–≥―É―Ä–Η), –Κ–Ψ–Η―²–Ψ ―¹–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Η –Ψ–±―Ä–Α–Ζ–Η –Β–¥–Η–Ϋ –Ϋ–Α –¥―Ä―É–≥. –ï–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Η―²–Β ―¹–Α –Ψ–±–Β–Κ―²–Η, –Κ–Ψ–Η―²–Ψ –Ϋ―è–Φ–Α―² ―Ü–Β–Ϋ―²―ä―Ä –Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è , ―².–Β. –Η–Φ–Α―â–Η ―¹–Α–Φ–Ψ ―Ä–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Α –Ψ―¹ –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è. –ê–Κ–Ψ ―²–Α–Κ―ä–≤ –Ψ–±–Β–Κ―² ―¹–Β –Ψ―²―Ä–Α–Ζ–Η –≤ –Ψ–≥–Μ–Β–¥–Α–Μ–Ψ, ―¹–Β –Ω–Ψ–Μ―É―΅–Α–≤–Α –Ψ–±–Β–Κ―², –Ϋ–Β―¹―ä–≤–Ω–Α–¥–Α―â ―¹ –Ψ―Ä–Η–≥–Η–Ϋ–Α–Μ–Α (–Ϋ–Α–Ι-–Ω―Ä–Ψ―¹―²–Η―è―² –Ω―Ä–Η–Φ–Β―Ä –Β –¥―è―¹–Ϋ–Α―²–Α –Η –Μ―è–≤–Α―²–Α ―Ä―ä–Κ–Α–≤–Η―Ü–Α.
–ö–Ψ–Ϋ―É―¹―ä―² –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ζ–Α–≤―ä―Ä―²–Α –Ϋ–Α–Μ―è–≤–Ψ –Η –Ϋ–Α–¥―è―¹–Ϋ–Ψ.¬†
2.¬†–™―Ä―É–Ω–Α βàû βÄΔ m, (–Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ¬†–Η¬†–±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ϋ–Α –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è).–Γ–Η–Φ–≤–Ψ–Μ―ä―² –Ϋ–Α –≥―Ä―É–Ω–Α―²–Α –Β¬†–Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Β–Ϋ –Κ–Ψ–Ϋ―É―¹. –™―Ä―É–Ω–Α―²–Α –Β –Ω–Ψ–Μ―è―Ä–Ϋ–Α, –Ϋ–Ψ –Ϋ–Β –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Α.
3.¬†–™―Ä―É–Ω–Α¬†βàû /m, (–Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ,¬†–Ϋ–Α–Ω―Ä–Β―΅–Ϋ–Α―²–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η ―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α –Η–Ϋ–≤–Β―Ä―¹–Η―è). –Δ–Α–Ζ–Η –≥―Ä―É–Ω–Α ―¹–Β –Ω―Ä–Β–¥―¹―²–Α–≤―è ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –≤―ä―Ä―²―è―â ―¹–Β ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä. –û―¹―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Β –Β –Ω–Ψ–Μ―è―Ä–Ϋ–Α, –¥–≤–Β―²–Β ―¹―²―Ä–Α–Ϋ–Η –Ϋ–Α ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä–Α ―¹―ä–≤–Ω–Α–¥–Α―² –Κ–Α―²–Ψ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Β –Ψ―² –Ϋ–Α–Ω―Ä–Β―΅–Ϋ–Α―²–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è.
4.¬†–™―Ä―É–Ω–Α βàû / 2, (–Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ¬†–Η¬†–±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ϋ–Α –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è 2). –€–Ψ–Ε–Β –¥–Α –±―ä–¥–Β –Ω―Ä–Β–¥―¹―²–Α–≤–Β–Ϋ–Α –Ψ―²¬†―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä, –Κ―Ä–Α–Η―â–Α―²–Α –Ϋ–Α –Κ–Ψ–Ι―²–Ψ ―¹–Α¬†―É―¹―É–Κ–Α–Ϋ–Η –≤ –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ–Η –Ω–Ψ―¹–Ψ–Κ–Η. –£ ―²–Α–Ζ–Η –≥―Ä―É–Ω–Α –Β –≤―ä–Ζ–Φ–Ψ–Ε–Β–Ϋ –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Η–Ζ―ä–Φ.
5.¬†–™―Ä―É–Ω–Α¬†βàû/mm, –Β–¥–Ϋ–Α –Ψ―¹ –Ϋ–Α –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ ―Ä–Β–¥, –Ϋ–Α–Ω―Ä–Β―΅–Ϋ–Η –Η –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ϋ–Α –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η –Ψ―¹–Η 2 –Η ―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è). –Γ–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α ―²–Α–Ζ–Η –≥―Ä―É–Ω–Α –Β ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α¬†–Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Ϋ–Η―è ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä.
6.¬†–™―Ä―É–Ω–Α¬†βàû /βàû, (―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ψ―¹–Η –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ, –±–Β–Ζ ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Η ―Ü–Β–Ϋ―²―Ä–Ψ–≤–Β –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è). –‰–Ζ–Ψ–±―Ä–Α–Ζ―è–≤–Α ―¹–Β –Κ–Α―²–Ψ ―¹–≤–Ψ–Β–Ψ–±―Ä–Α–Ζ–Ϋ–Α ―¹―³–Β―Ä–Α, –Ϋ–Α –Κ–Ψ―è―²–Ψ –≤―¹–Η―΅–Κ–Η –¥–Η–Α–Φ–Β―²―Ä–Η ―¹–Α ―É―¹―É–Κ–Α–Ϋ –Ϋ–Α–Μ―è–≤–Ψ –Η–Μ–Η –Ϋ–Α–¥―è―¹–Ϋ–Ψ, ―¹―ä–Ψ―²–≤–Β―²–≤–Α―â–Η –Ϋ–Α –Μ―è–≤–Α –Η –¥―è―¹–Ϋ–Α –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Α ―³–Ψ―Ä–Φ–Α.
7.¬†–™―Ä―É–Ω–Α βàû /βàû m¬†, (―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ψ―¹–Η –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ –Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è). –û–Ω–Η―¹–≤–Α ―¹–Β –Ψ―² ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Α –Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Ϋ–Α ―¹―³–Β―Ä–Α.
–Γ–Κ–Α–Μ–Α―Ä–Η, –≤–Β–Κ―²–Ψ―Ä–Η –Η ―²–Β–Ϋ–Ζ–Ψ―Ä–Η
–ù–Β–Κ–Α ―¹–Β –Ζ–Α–Ω–Ψ–Ζ–Ϋ–Α–Β–Φ (–Η–Μ–Η –¥–Α ―¹–Η –Ω―Ä–Η–Ω–Ψ–Φ–Ϋ–Η–Φ) –Ϋ―è–Κ–Ψ–Η –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Η –Ω–Ψ–Ϋ―è―²–Η―è, –Φ–Ϋ–Ψ–≥–Ψ –≤–Α–Ε–Ϋ–Η –Ζ–Α –≤―Ä―ä–Ζ–Κ–Α―²–Α –Φ–Β–Ε–¥―É ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α, –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Α―²–Α –Η ―³–Η–Ζ–Η–Κ–Α―²–Α.
–Γ–Κ–Α–Μ–Α―Ä
–Γ–Κ–Α–Μ–Α―Ä―ä―² (–Ψ―² –Μ–Α―².¬†scala¬†βÄî ―¹―²―ä–Μ–±–Α) –Β –≤–Β–Μ–Η―΅–Η–Ϋ–Α (–Ω―Ä–Ψ–Φ–Β–Ϋ–Μ–Η–≤–Α) –≤―¹―è–Κ–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² –Ϋ–Α –Κ–Ψ―è―²–Ψ –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Η–Ζ―Ä–Α–Ζ–Η ―¹ –Β–¥–Ϋ–Ψ ―΅–Η―¹–Μ–Ψ (–Ϋ–Α–Ι-―΅–Β―¹―²–Ψ –≤–Β―â–Β―¹―²–≤–Β–Ϋ–Ψ).¬†–ü―Ä–Η ―¹–Φ―è–Ϋ–Α –Ϋ–Α –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²–Ϋ–Α―²–Α ―¹–Η―¹―²–Β–Φ–Α ―¹–Κ–Α–Μ–Α―Ä―ä―² –Ψ―¹―²–Α–≤–Α –Ϋ–Β–Ω―Ä–Ψ–Φ–Β–Ϋ–Β–Ϋ (–Η–Ϋ–≤–Α―Ä–Η–Α–Ϋ―²–Β–Ϋ). –£ ―¹―ä–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Α―²–Α ―³–Η–Ζ–Η–Κ–Α, ―¹–Κ–Α–Μ–Α―Ä –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ψ ―¹–Β ―Ä–Α–Ζ–±–Η―Ä–Α –Κ–Α―²–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Β–Ϋ–Ψ-–≤―Ä–Β–Φ–Β–≤–Η ―¹–Κ–Α–Μ–Α―Ä, –Κ–Ψ–Ι―²–Ψ –Ϋ–Β ―¹–Β –Ω―Ä–Ψ–Φ–Β–Ϋ―è –Ω―Ä–Η –Ω―Ä–Β―Ö–Ψ–¥ –Ψ―² –Β–¥–Ϋ–Α –Η–Ϋ–Β―Ä―Ü–Η–Α–Μ–Ϋ–Α ―¹–Η―¹―²–Β–Φ–Α –Ϋ–Α –Ψ―²―΅–Η―²–Α–Ϋ–Β –≤ –¥―Ä―É–≥–Α, –Α –≤ ―¹―ä–≥–Μ–Α―¹–Η–Β ―¹ –û–±―â–Α―²–Α ―²–Β–Ψ―Ä–Η―è –Ϋ–Α –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ―¹―²―²–Α - –Η –Ω―Ä–Η –Ω―Ä–Β―Ö–Ψ–¥ –Φ–Β–Ε–¥―É –Ϋ–Β–Η–Ϋ–Β―Ä―Ü–Η–Α–Μ–Ϋ–Η ―¹–Η―¹―²–Β–Φ–Η. –ö–Α–Κ–≤–Ψ –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α ―²–Ψ–≤–Α –≤ ―Ä–Α–Ζ–¥–Β–Μa –Ζ–Α –Δ–Β–Ψ―Ä–Η―è―²–Α –Ϋ–Α –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ―¹―²―²–Α.
–Γ–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α ―¹–Κ–Α–Μ–Α―Ä–Α ―¹–Β ―¹―ä–Ω–Ψ―¹―²–Α–≤―è ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α ―¹―³–Β―Ä–Α - ―Ä–Α–Ζ–Φ–Β―Ä―ä―² –Ι ―¹―ä―â–Ψ –Β –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ –Ψ―² –Β–¥–Ϋ–Ψ ―΅–Η―¹–Μ–Ψ - ―Ä–Α–¥–Η―É―¹–Α. –ü―Ä–Η–Φ–Β―Ä –Ζ–Α ―¹–Κ–Α–Μ–Α―Ä –Β –Φ–Α―¹–Α―²–Α –Ω―Ä–Η –Ω–Ψ–Κ–Ψ–Ι –Ϋ–Α ―²–Β–Μ–Α―²–Α, –Κ–Ψ―è―²–Ψ –Β –Η–Ϋ–≤–Α―Ä–Η–Α–Ϋ―²–Ϋ–Α –Ζ–Α –≤―¹–Η―΅–Κ–Η –Η–Ϋ–Β―Ä―Ü–Η–Α–Μ–Ϋ–Η –Η –Ϋ–Β–Η–Ϋ–Β―Ä―Ü–Η–Α–Μ–Ϋ–Η ―¹–Η―¹―²–Β–Φ–Η. –‰–Ζ–Ψ–±―â–Ψ –≤―¹–Η―΅–Κ–Η ―³–Η–Ζ–Η―΅–Ϋ–Η –≤–Β–Μ–Η―΅–Η–Ϋ–Η, –Κ–Ψ–Η―²–Ψ –Ϋ–Β –Ζ–Α–≤–Η―¹―è―² –Ψ―² –Ω–Ψ―¹–Ψ–Κ–Α―²–Α ―¹–Α ―¹–Κ–Α–Μ–Α―Ä–Ϋ–Η
–ü―¹–Β–≤–¥–Ψ―¹–Κ–Α–Μ–Α―Ä
–ü―¹–Β–≤–¥–Ψ―¹–Κ–Α–Μ–Α―Ä―ä―² –Β –≤–Β–Μ–Η―΅–Η–Ϋ–Α, –Κ–Ψ―è―²–Ψ –Ϋ–Β ―¹–Β –Ω―Ä–Ψ–Φ–Β–Ϋ―è –Ω―Ä–Η –Ω―Ä–Β–Φ–Β―¹―²–≤–Α–Ϋ–Β –Η –Ζ–Α–≤―ä―Ä―²–Α–Ϋ–Β –Ϋ–Α –Κ–Ψ–Ψ―Ä–¥–Η–Ϋ–Α―²–Ϋ–Η―²–Β –Ψ―¹–Η, –Ϋ–Ψ –Ω―Ä–Ψ–Φ–Β–Ϋ―è –Ζ–Ϋ–Α–Κ–Α ―¹–Η –Ω―Ä–Η ―¹–Φ―è–Ϋ–Α –Ϋ–Α –Ω–Ψ―¹–Ψ–Κ–Α―²–Α –Ϋ–Α –≤―¹―è–Κ–Α –Ψ―¹ ―¹ –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ–Α―²–Α –Ι. –ü―Ä–Η–Φ–Β―Ä –Ζ–Α –Ω―¹–Β–≤–¥–Ψ―¹–Κ–Α–Μ–Α―Ä –≤―ä–≤ ―³–Η–Ζ–Η–Κ–Α―²–Α –Β –Φ–Α–≥–Ϋ–Η―²–Ϋ–Η―è –Ζ–Α―Ä―è–¥.
–£–Β–Κ―²–Ψ―Ä
–£–Β–Κ―²–Ψ―Ä―ä―², –Κ–Α–Κ―²–Ψ –Φ–Ϋ–Ψ–Ζ–Η–Ϋ–Α ―¹–Η ―¹–Ω–Ψ–Φ–Ϋ―è―² –Β –Ϋ–Α―¹–Ψ―΅–Β–Ϋ–Α –Ψ―²―¹–Β―΅–Κ–Α, –≤–Β–Μ–Η―΅–Η–Ϋ–Α, –Κ–Ψ―è―²–Ψ ―¹–Β –Ψ–Ω―Ä–Β–¥–Β–Μ―è –Ψ―² ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² (―¹–Κ–Α–Μ–Α―Ä) –Η –Ω–Ψ―¹–Ψ–Κ–Α. –ü―Ä–Η–Φ–Β―Ä–Η―²–Β –Ϋ–Α –Ϋ–Α―¹–Ψ―΅–Β–Ϋ–Η –≤–Β–Μ–Η―΅–Η–Ϋ–Α –≤―ä–≤ ―³–Η–Ζ–Η–Κ–Α―²–Α ―¹–Α –Φ–Ϋ–Ψ–≥–Ψ: ―¹–Η–Μ–Α, ―¹–Κ–Ψ―Ä–Ψ―¹―², –Φ–Ψ–Φ–Β–Ϋ―²... –Γ–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –≤–Β–Κ―²–Ψ―Ä–Α –Β ―¹–≤―ä―Ä–Ζ–≤–Α–Ϋ–Α ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –Κ–Ψ–Ϋ―É―¹–Α.
–£–Β–Κ―²–Ψ―Ä–Η―²–Β ―¹–Α –¥–≤–Α –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Η –≤–Η–¥–Α:
|
 –ü―Ä–Η–Φ–Β―Ä –Ζ–Α –Α–Κ―¹–Η–Α–Μ–Β–Ϋ –≤–Β–Κ―²–Ψ―Ä –Β –≤–Β–Κ―²–Ψ―Ä–Ϋ–Ψ―²–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Ϋ–Α –¥–≤–Α –≤–Β–Κ―²–Ψ―Ä–Α. –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è: wikipedia –ü―Ä–Η–Φ–Β―Ä –Ζ–Α –Α–Κ―¹–Η–Α–Μ–Β–Ϋ –≤–Β–Κ―²–Ψ―Ä –Β –≤–Β–Κ―²–Ψ―Ä–Ϋ–Ψ―²–Ψ –Ω―Ä–Ψ–Η–Ζ–≤–Β–¥–Β–Ϋ–Η–Β –Ϋ–Α –¥–≤–Α –≤–Β–Κ―²–Ψ―Ä–Α. –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è: wikipedia |
–Δ–Β–Ϋ–Ζ–Ψ―Ä
–Δ―Ä–Β―²–Η―è―² ―³―É–Ϋ–¥–Α–Φ–Β–Ϋ―²–Α–Μ–Β–Ϋ –≥–Β–Ψ–Φ–Β―²―Ä–Η―΅–Β–Ϋ –Ψ–±–Β–Κ―² –Β ―²–Β–Ϋ–Ζ–Ψ―Ä―ä―². –‰–Φ–Β―²–Ψ –Φ―É –Β –Ψ―²¬†–Μ–Α―²–Η–Ϋ―¹–Κ–Η –Ω―Ä–Ψ–Η–Ζ―Ö–Ψ–¥¬†tensus,"–Ϋ–Α–Ω―Ä–Β–≥–Ϋ–Α―²" - –Β–¥–Ϋ–Α –Ψ―² ―³―É–Ϋ–Κ―Ü–Η–Η―²–Β –Ϋ–Α ―²–Ψ–≤–Α –Ω–Ψ–Ϋ―è―²–Η–Β –Β –¥–Α –Η–Ζ―Ä–Α–Ζ―è–≤–Α ―¹―ä―¹―²–Ψ―è–Ϋ–Η–Β―²–Ψ –Ϋ–Α –Ϋ–Α–Ω―Ä–Β–Ε–Β–Ϋ–Η–Β –Ϋ–Α ―²–Β–Μ–Α―²–Α. –Δ–Β–Ϋ–Ζ–Ψ―Ä–Η―²–Β –Ψ―¹–Η–≥―É―Ä―è–≤–Α―² –Μ–Β―¹–Β–Ϋ –Η –Κ―Ä–Α―²―ä–Κ –Ϋ–Α―΅–Η–Ϋ –Ζ–Α –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Ψ ―³–Ψ―Ä–Φ―É–Μ–Η―Ä–Α–Ϋ–Β –Η ―Ä–Β―à–Α–≤–Α–Ϋ–Β –Ϋ–Α –Ω―Ä–Ψ–±–Μ–Β–Φ–Η –≤ –Ψ–±–Μ–Α―¹―²―²–Α –Ϋ–Α ―³–Η–Ζ–Η–Κ–Α―²–Α, –Κ–Α―²–Ψ ―²–Β–Ψ―Ä–Η―è―²–Α –Ϋ–Α –Β–Μ–Α―¹―²–Η―΅–Ϋ–Ψ―¹―²―²–Α, –Φ–Β―Ö–Α–Ϋ–Η–Κ–Α―²–Α –Ϋ–Α ―³–Μ―É–Η–¥–Η―²–Β, –Κ–Α–Κ―²–Ψ –Η –Ψ–±―â–Α―²–Α ―²–Β–Ψ―Ä–Η―è –Ϋ–Α –Ψ―²–Ϋ–Ψ―¹–Η―²–Β–Μ–Ϋ–Ψ―¹―²―²–Α. –Δ–Β–Ϋ–Ζ–Ψ―Ä―ä―² ―¹–Β –Ψ–Ω–Η―¹–≤–Α o―² –Φ–Ϋ–Ψ–≥–Ψ–Φ–Β―Äe–Ϋ¬†–Φ–Α―¹–Η–≤, ―²–Ψ–Β―¹―² –Ω–Ψ–¥―Ä–Β–¥–Β–Ϋ–Α –≥―Ä―É–Ω–Α ―΅–Η―¹–Μ–Α, –Κ–Α―²–Ψ –Φ―è―¹―²–Ψ―²–Ψ –Ϋ–Α –≤―¹―è–Κ–Ψ ―΅–Η―¹–Μ–Ψ –Β –Ψ–Ω―Ä–Β–¥–Β–Μ–Β–Ϋ–Ψ –Ψ―² –Η–Ϋ–¥–Β–Κ―¹–Η―²–Β –Φ―É. –Δ–Β–Ϋ–Ζ–Ψ―Ä―ä―² –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Κ–Α–Ε–Β –Β n-–Φ–Β―Ä–Ϋ–Α ―²–Α–±–Μ–Η―Ü–Α, –Κ–Α―²–Ψ n –Β¬†–≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―²―²–Α (–Ω–Ψ―Ä―è–¥―ä–Κ–Α) –Ϋ–Α ―²–Β–Ϋ–Ζ–Ψ―Ä–Α. –Δ–Β–Ϋ–Ζ–Ψ―Ä ―¹ –Ϋ―É–Μ–Β–≤–Α –≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―² –Β ―¹–Κ–Α–Μ–Α―Ä, –Α ―¹ –≤–Α–Μ–Β–Ϋ―²–Ϋ–Ψ―¹―² 1 - –Β –≤–Β–Κ―²–Ψ―Ä.
–£–¥―è―¹–Ϋ–Ψ –Β ―¹―Ö–Β–Φ–Α –Ϋ–Α ―²–Β–Ϋ–Ζ–Ψ―Ä –Ϋ–Α –Φ–Β―Ö–Α–Ϋ–Η―΅–Ϋ–Ψ―²–Ψ –Ϋ–Α–Ω―Ä–Β–Ε–Β–Ϋ–Η–Β –Ψ―² ―²―Ä–Β―²–Η –Ω–Ψ―Ä―è–¥―ä–Κ. –ö–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Η―²–Β –Ϋ–Α ―²–Β–Ϋ–Ζ–Ψ―Ä–Α ( –Ζ–Α ―¹―²–Β–Ϋ–Η―²–Β –Ϋ–Α –Β–Μ–Β–Φ–Β–Ϋ―²–Α―Ä–Ϋ–Η―è –Κ―É–± e1, e2, e3, –Ω–Β―Ä–Ω–Β–Ϋ–¥–Η–Κ―É–Μ―è―Ä–Ϋ–Η –Ϋ–Α –Ψ―¹–Η: x1, x2, x3) –≤ ―²―Ä–Η–Φ–Β―Ä–Ϋ–Α―²–Α –¥–Β–Κ–Α―Ä―²–Ψ–≤–Α ―¹–Η―¹―²–Β–Φa –Ψ–±―Ä–Α–Ζ―É–≤–Α―² –Φ–Α―²―Ä–Η―Ü–Α―²–Α: œÉ=[T(e1)T(e2)T(e3)] .–Δ–Β–Ζ–Η ―¹–Η–Μ–Η ―¹–Α –Ω―Ä–Β–¥―¹―²–Α–≤–Β–Ϋ–Η –Ψ―²¬†–Κ–Ψ–Μ–Ψ–Ϋ–Η―²–Β –≤–Β–Κ―²–Ψ―Ä–Η¬†.¬†–Δ–Β–Ϋ–Ζ–Ψ―Ä―ä―² –Φ–Ψ–Ε–Β –¥–Α –±―ä–¥–Β –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–≤–Α–Ϋ –Ψ―² –Φ–Α―²―Ä–Η―Ü–Α―²–Α:  ¬† ¬† |
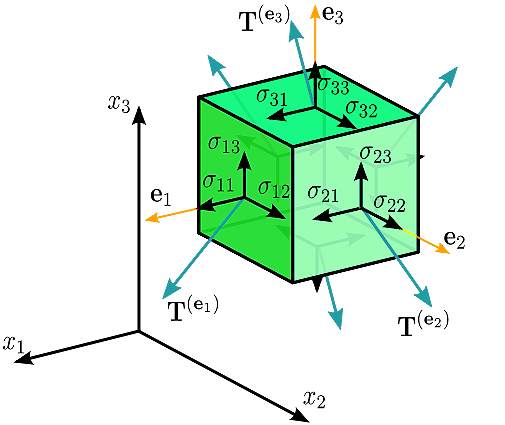 –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è: wikipedia –‰–Μ―é―¹―²―Ä–Α―Ü–Η―è: wikipedia |
–Δ–Β–Ϋ–Ζ–Ψ―Ä–Η―²–Β, ―¹―ä―â–Ψ –Κ–Α―²–Ψ –≤–Β–Κ―²–Ψ―Ä–Η―²–Β, ―¹–Α –Ϋ–Α―¹–Ψ―΅–Β–Ϋ–Η –≤–Β–Μ–Η―΅–Η–Ϋ–Η, –Κ–Ψ–Η―²–Ψ ―¹―ä―â–Ψ –Κ–Α―²–Ψ ―²―è―Ö –Φ–Ψ–≥–Α―² –¥–Α –±―ä–¥–Α―² –Ω–Ψ–Μ―è―Ä–Ϋ–Η –Η–Μ–Η –Α–Κ―¹–Η–Α–Μ–Ϋ–Η. –ü–Ψ–Μ―è―Ä–Ϋ–Η―²–Β ―²–Β–Ϋ–Ζ–Ψ―Ä–Η ―¹–Α ―Ä–Β–Ζ―É–Μ―²–Α―² –Ψ―² –Μ–Η–Ϋ–Β–Ι–Ϋ–Α –≤―Ä―ä–Ζ–Κ–Α –Φ–Β–Ε–¥―É –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Η―²–Β –Ϋ–Α –¥–≤–Α –Ω–Ψ–Μ―è―Ä–Ϋ–Η –Η–Μ–Η –¥–≤–Α –Α–Κ―¹–Η–Α–Μ–Ϋ–Η –≤–Β–Κ―²–Ψ―Ä–Α, –Α –Α–Κ―¹–Η–Α–Μ–Ϋ–Η―²–Β - –Φ–Β–Ε–¥―É –Κ–Ψ–Φ–Ω–Ψ–Ϋ–Β–Ϋ―²–Η―²–Β –Ϋ–Α –Ω–Ψ–Μ―è―Ä–Β–Ϋ –Η –Α–Κ―¹–Η–Α–Μ–Β–Ϋ –≤–Β–Κ―²–Ψ―Ä.
–£―Ä―ä–Ζ–Κ–Α –Ϋ–Α –Ω―Ä–Β–¥–Β–Μ–Ϋ–Η―²–Β –≥―Ä―É–Ω–Η ―¹ ―è–≤–Μ–Β–Ϋ–Η―è –≤―ä–≤ ―³–Η–Ζ–Η–Κ–Α―²–Α
–Γ–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α ―¹―³–Β―Ä–Α―²–Α –Β –Φ–Α–Κ―¹–Η–Φ–Α–Μ–Ϋ–Ψ –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Α―²–Α ―²–Ψ―΅–Κ–Ψ–≤–Α ―¹–Η–Φ–Β―²―Ä–Η―è –≤ ―²―Ä–Η–Φ–Β―Ä–Ϋ–Ψ―²–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ –Κ–Α―²–Ψ –≤―¹–Η―΅–Κ–Η ―²–Ψ―΅–Κ–Ψ–≤–Η –≥―Ä―É–Ω–Η –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–≤–Α―² –Ω–Ψ–¥–≥―Ä―É–Ω–Η –Ϋ–Α –≥―Ä―É–Ω–Α―²–Α –Ϋ–Α ―¹―³–Β―Ä–Α―²–Α. –£ –Φ–Α―²–Β–Φ–Α―²–Η–Κ–Α―²–Α –Η ―²–Β–Ψ―Ä–Β―²–Η―΅–Ϋ–Α―²–Α ―³–Η–Ζ–Η–Κ–Α ―²–Β–Ζ–Η –≥―Ä―É–Ω–Η –Ζ–Α ―²―Ä–Η–Φ–Β―Ä–Ϋ–Ψ―²–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ ―¹–Β –Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α―² ―¹―ä―¹ SO(3) (―¹–Ω–Β―Ü–Η–Α–Μ–Ϋ–Α –Ψ―Ä―²–Ψ–≥–Ψ–Ϋ–Α–Μ–Ϋ–Α –≥―Ä―É–Ω–Α) –Η O(3) (–Ψ―Ä―²–Ψ–≥–Ψ–Ϋ–Α–Μ–Ϋ–Α –≥―Ä―É–Ω–Α).
–£―¹―è–Κ–Ψ –¥–≤–Η–Ε–Β–Ϋ–Η–Β –Φ–Ψ–Ε–Β –¥–Α ―¹–Β ―Ä–Α–Ζ–Μ–Ψ–Ε–Η –Ϋ–Α –Ω–Ψ―¹―²―ä–Ω–Α―²–Β–Μ–Ϋ–Ψ (―²―Ä–Α–Ϋ―¹–Μ–Α―Ü–Η―è) –Η –≤―ä―Ä―²–Β–Μ–Η–≤–Ψ (―Ä–Ψ―²–Α―Ü–Η―è) –Η ―²―ä–Κ –Κ–Α―²–Ψ –¥–≤–Η–Ε–Β–Ϋ–Η–Β―²–Ψ –Η–Φ–Α ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –≤–Β–Κ―²–Ψ―Ä, ―²–Ψ –Ω―Ä–Η ―²―Ä–Α–Ϋ―¹–Μ–Α―Ü–Η―è ―²–Ψ–Ι –Β –Ω–Ψ–Μ―è―Ä–Β–Ϋ, –Α –Ω―Ä–Η ―Ä–Ψ―²–Α―Ü–Η―è - –Α–Κ―¹–Η–Α–Μ–Β–Ϋ.
–ü―Ä–Β–¥–Β–Μ–Ϋ–Η―²–Β –≥―Ä―É–Ω–Η –Ϋ–Α –ö―é―Ä–Η ―¹–Β ―¹–≤―ä―Ä–Ζ–≤–Α―² ―¹ –Ϋ―è–Κ–Ψ–Η –Ψ―¹–Ϋ–Ψ–≤–Ϋ–Η –Φ–Α―²–Β–Φ–Α―²–Η―΅–Ϋ–Η –Η ―³–Η–Ζ–Η―΅–Ϋ–Η –≤–Β–Μ–Η―΅–Η–Ϋ–Η: –™―Ä–Α–≤–Η―²–Α―Ü–Η–Ψ–Ϋ–Ϋ–Ψ―²–Ψ –Ω–Ψ–Μ–Β ―¹–Β –Ψ–Ω–Η―¹–≤–Α ―¹ –Ω–Ψ–Μ―è―Ä–Β–Ϋ ―²–Β–Ϋ–Ζ–Ψ―Ä –Η –Η–Φ–Α ―¹–Η–Φ–Β―²―Ä–Η―è βàû /mm. –Γ–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –Β–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Ψ―²–Ψ –Β–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Ψ –Ω–Ψ–Μ–Β ―¹–Β ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Η–Ζ–Η―Ä–Α ―¹ –≥―Ä―É–Ω–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α –Κ–Ψ–Ϋ―É―¹ ¬†βàû βÄΔ m, –Β–¥–Ϋ–Ψ―Ä–Ψ–¥–Ϋ–Ψ―²–Ψ –Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ –Ω–Ψ–Μ–Β -¬† ―¹ –≥―Ä―É–Ω–Α―²–Α –Ϋ–Α¬† ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α¬†―Ä–Ψ―²–Α―Ü–Η–Ψ–Ϋ–Β–Ϋ¬† ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä βàû /m, –¥–Β―³–Ψ―Ä–Φ–Α―Ü–Η–Η―²–Β –Ω―Ä–Η –Β–¥–Ϋ–Ψ–Ψ―¹–Β–Ϋ –Ψ–Ω―ä–Ϋ –Η–Μ–Η –Ϋ–Α―²–Η―¹–Κ - ―¹ –≥―Ä―É–Ω–Α―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α –Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Β–Ϋ ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä βàû β¹³ mm, ―²–Ψ–Ω–Μ–Η–Ϋ–Ϋ–Ψ―²–Ψ ―Ä–Α–Ζ―à–Η―Ä–Β–Ϋ–Η–Β - ―¹ –≥―Ä―É–Ω–Α―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Α –Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Ϋ–Α ―¹―³–Β―Ä–Α βàû β¹³ βàû βÄΔ ¬†m.
–ü―Ä–Η–Μ–Α–≥–Α–Φ –Β–¥–Ϋ–Α ―²–Α–±–Μ–Η―Ü–Α, –Κ–Ψ―è―²–Ψ –¥–Α –Ψ–±–Ψ–±―â–Η ―²–Β–Ζ–Η –Η–Ϋ―²–Β―Ä–Β―¹–Ϋ–Η –≤―Ä―ä–Ζ–Κ–Η –Φ–Β–Ε–¥―É –Ω―Ä–Β–¥–Β–Μ–Ϋ–Η―²–Β ―³–Ψ―Ä–Φ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, ―¹–Κ–Α–Μ–Α―Ä–Α, –≤–Β–Κ―²–Ψ―Ä–Α –Η ―²–Β–Ϋ–Ζ–Ψ―Ä–Α –Η –Ϋ―è–Κ–Ψ–Η ―³–Η–Ζ–Η―΅–Β―¹–Κ–Η ―¹–≤–Ψ–Ι―¹―²–≤–Α –Η ―è–≤–Μ–Β–Ϋ–Η―è:
| –ü―Ä–Β–¥–Β–Μ–Ϋ–Η –≥―Ä―É–Ω–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è/ | –€–Α―²–Β–Φ–Α- ―²–Η―΅–Β―¹–Κ–Α –≤–Β–Μ–Η―΅–Η–Ϋ–Α | –û–Ω–Η―¹–Α–Ϋ–Η–Β | –î–Ψ–Ω―ä–Μ–Ϋ–Β–Ϋ–Η–Β |
|---|---|---|---|
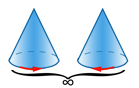 |
–ê–Κ―¹–Η–Α–Μ–Β–Ϋ –≤–Β–Κ―²–Ψ―Ä | –™―Ä―É–Ω–Α βàû, –Β–¥–Ϋ–Α –Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ. –Δ―è ―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Α –Ϋ–Α ―Ä–Α–≤–Ϋ–Ψ–Φ–Β―Ä–Ϋ–Ψ –≤―ä―Ä―²―è―â ―¹–Β –Κ–Ψ–Ϋ―É―¹. –ö–Ψ–Ϋ―É―¹―ä―² –Φ–Ψ–Ε–Β –¥–Α ―¹–Β –Ζ–Α–≤―ä―Ä―²–Α –Ϋ–Α–Μ―è–≤–Ψ –Η –Ϋ–Α–¥―è―¹–Ϋ–Ψ. –™―Ä―É–Ω–Α –Β –Ω–Ψ–Μ―è―Ä–Ϋ–Α –Η –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Α (―Ö–Η―Ä–Α–Μ–Ϋ–Α) | –Γ–≤―ä―Ä–Ζ–≤–Α ―¹–Β ―¹ –≤―ä―Ä―²–Β–Μ–Η–≤–Ψ –¥–≤–Η–Ε–Β–Ϋ–Η–Β –Η –¥–≤–Η–Ε–Β–Ϋ–Η–Β –≤ –Κ―Ä―ä–≥, –Κ–Α–Κ―²–Ψ –Η ―¹–≤–Ψ–Ι―¹―²–≤–Ψ―²–Ψ –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Ψ―¹―² - ―¹–Ω–Ψ―¹–Ψ–±–Ϋ–Ψ―¹―²―²–Α –Ϋ–Α –Κ―Ä–Η―¹―²–Α–Μ–Η―²–Β –¥–Α ―¹―ä―â–Β―¹―²–≤―É–≤–Α―² –≤ –¥–≤–Β –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Η –Η–Ζ–Ψ–Φ–Β―Ä–Ϋ–Η (–Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Η) ―³–Ψ―Ä–Φ–Η. –ù–Α–Ω―Ä–Η–Φ–Β―Ä –Κ–≤–Α―Ä―Ü―ä―² ―¹–Β ―è–≤―è–≤–Α –≤ –¥–Β―¹–Ϋ–Η –Η –Μ–Β–≤–Η ―³–Ψ―Ä–Φ–Η, –Κ–Ψ–Η―²–Ψ ―¹–Α –Ψ–≥–Μ–Β–¥–Α–Μ–Ϋ–Η –Ψ–±―Ä–Α–Ζ–Η –Β–¥–Η–Ϋ –Ϋ–Α –¥―Ä―É–≥ |
 |
–ü–Ψ–Μ―è―Ä–Β–Ϋ –≤–Β–Κ―²–Ψ―Ä |
–™―Ä―É–Ω–Α βàû βÄΔ m, –Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ¬†–Η¬†–±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ϋ–Α –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è. –Γ–Η–Φ–≤–Ψ–Μ―ä―² –Ϋ–Α –≥―Ä―É–Ω–Α―²–Α –Β¬†–Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Β–Ϋ –Κ–Ψ–Ϋ―É―¹. –™―Ä―É–Ω–Α―²–Α –Β –Ω–Ψ–Μ―è―Ä–Ϋ–Α, –Ϋ–Ψ –Ϋ–Β –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Α. |
–Γ–≤―ä―Ä–Ζ–≤–Α ―¹–Β ―¹ ―è–≤–Μ–Β–Ϋ–Η―è, ―¹–≤―ä―Ä–Ζ–Α–Ϋ–Η ―¹ –Ϋ–Α―¹–Ψ―΅–Β–Ϋ–Ψ –¥–≤–Η–Ε–Β–Ϋ–Η–Β: ―¹–Κ–Ψ―Ä–Ψ―¹―², ―É―¹–Κ–Ψ―Ä–Β–Ϋ–Η–Β, ―¹–Η–Μ–Α, –Β–Ϋ–Β―Ä–≥–Η―è. |
 |
–ê–Κ―¹–Η–Α–Μ–Β–Ϋ –Δ–Β–Ϋ–Ζ–Ψ―Ä | –™―Ä―É–Ω–Α¬†βàû /m, –Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ,¬†–Ϋ–Α–Ω―Ä–Β―΅–Ϋ–Α―²–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η ―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α –Η–Ϋ–≤–Β―Ä―¹–Η―è. –Δ–Α–Ζ–Η –≥―Ä―É–Ω–Α ―¹–Β –Ω―Ä–Β–¥―¹―²–Α–≤―è ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –≤―ä―Ä―²―è―â ―¹–Β ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä. –û―¹―²–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Ϋ–Β –Β –Ω–Ψ–Μ―è―Ä–Ϋ–Α, –¥–≤–Β―²–Β ―¹―²―Ä–Α–Ϋ–Η –Ϋ–Α ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä–Α ―¹―ä–≤–Ω–Α–¥–Α―² –Κ–Α―²–Ψ –≤–Ζ–Α–Η–Φ–Ϋ–Ψ –Ψ―²―Ä–Α–Ε–Β–Ϋ–Η–Β –Ψ―² –Ϋ–Α–Ω―Ä–Β―΅–Ϋ–Α―²–Α ―Ä–Α–≤–Ϋ–Η–Ϋ–Α –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è. | –Δ–Ψ–≤–Α –Β ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –Ω–Ψ―¹―²–Ψ―è–Ϋ–Ϋ–Η―è –Φ–Α–≥–Ϋ–Η―² –Η –Φ–Α–≥–Ϋ–Η―²–Ϋ–Ψ―²–Ψ –Ω–Ψ–Μ–Β –Ϋ–Α –Ω―Ä–Α–≤–Η―è ―²–Ψ–Κ |
 |
–Δ–Β–Ϋ–Ζ–Ψ―Ä | ¬†–™―Ä―É–Ω–Α βàû / 2, (–Ψ―¹ ―¹―ä―¹ ―¹–Η–Φ–Β―²―Ä–Η―è –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ¬†–Η¬†–±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ϋ–Α –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è 2). –€–Ψ–Ε–Β –¥–Α –±―ä–¥–Β –Ω―Ä–Β–¥―¹―²–Α–≤–Β–Ϋ–Α –Ψ―²¬†―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä, –Κ―Ä–Α–Η―â–Α―²–Α –Ϋ–Α –Κ–Ψ–Ι―²–Ψ ―¹–Α¬†―É―¹―É–Κ–Α–Ϋ–Η –≤ –Ω―Ä–Ψ―²–Η–≤–Ψ–Ω–Ψ–Μ–Ψ–Ε–Ϋ–Η –Ω–Ψ―¹–Ψ–Κ–Η. | –£ ―²–Α–Ζ–Η –≥―Ä―É–Ω–Α –Β –≤―ä–Ζ–Φ–Ψ–Ε–Β–Ϋ –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Η–Ζ―ä–Φ. –Δ–Α–Ζ–Η ―¹–Η–Φ–Β―²―Ä–Η―è –Β ―Ö–Α―Ä–Α–Κ―²–Β―Ä–Ϋ–Α –Ζ–Α –Ω–Ψ–Μ―è―Ä–Η–Ζ–Α―Ü–Η―è –≤ –Α–Ϋ–Η–Ζ–Ψ―²―Ä–Ψ–Ω–Ϋ–Α ―¹―Ä–Β–¥–Α |
 |
–ü–Ψ–Μ―è―Ä–Β–Ϋ –Δ–Β–Ϋ–Ζ–Ψ―Ä |
–™―Ä―É–Ω–Α βàû/mm, –Β–¥–Ϋ–Α –Ψ―¹ –Ϋ–Α –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ ―Ä–Β–¥, –Ϋ–Α–Ω―Ä–Β―΅–Ϋ–Η –Η –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η –±–Β–Ζ–Κ―Ä–Α–Ι–Ϋ–Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è, –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ϋ–Α –Ϋ–Α–¥–Μ―ä–Ε–Ϋ–Η –Ψ―¹–Η 2 –Η ―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è). –Γ–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α ―²–Α–Ζ–Η –≥―Ä―É–Ω–Α –Β ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α¬†–Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Ϋ–Η―è ―Ü–Η–Μ–Η–Ϋ–¥―ä―Ä.¬† |
–Δ–Α–Κ–Α–≤–Α –Β ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –Φ–Β―Ö–Α–Ϋ–Η―΅–Ϋ–Α ―¹–Η–Μ–Α ―¹ –Β–¥–Ϋ–Ψ–Ψ―¹–Ψ–≤ –Ϋ–Α―²–Η―¹–Κ (–Ψ–Ω―ä–Ϋ). |
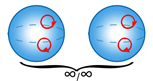 |
–ü―¹–Β–≤–¥–Ψ-―¹–Κ–Α–Μ–Α―Ä | –™―Ä―É–Ω–Α¬†βàû /βàû, (―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ψ―¹–Η –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ, –±–Β–Ζ ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Η ―Ü–Β–Ϋ―²―Ä–Ψ–≤–Β –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è). –‰–Ζ–Ψ–±―Ä–Α–Ζ―è–≤–Α ―¹–Β –Κ–Α―²–Ψ ―¹–≤–Ψ–Β–Ψ–±―Ä–Α–Ζ–Ϋ–Α ―¹―³–Β―Ä–Α, –Ϋ–Α –Κ–Ψ―è―²–Ψ –≤―¹–Η―΅–Κ–Η –¥–Η–Α–Φ–Β―²―Ä–Η ―¹–Α ―É―¹―É–Κ–Α–Ϋ –Ϋ–Α–Μ―è–≤–Ψ –Η–Μ–Η –Ϋ–Α–¥―è―¹–Ϋ–Ψ, ―¹―ä–Ψ―²–≤–Β―²–≤–Α―â–Η –Ϋ–Α –Μ―è–≤–Α –Η –¥―è―¹–Ϋ–Α –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Α ―³–Ψ―Ä–Φ–Α. | –Γ―ä–Ψ―²–≤–Β―²―¹―²–≤–Α –Ϋ–Α –¥–Β―¹–Ϋ–Η –Η –Μ–Β–≤–Η –Β–Ϋ–Α–Ϋ―²–Η–Ψ–Φ–Ψ―Ä―³–Ϋ–Η ―³–Ψ―Ä–Φ–Η. |
 |
–Γ–Κ–Α–Μ–Α―Ä |
–™―Ä―É–Ω–Α βàû /βàû m¬†, (―Ü–Β–Ϋ―²―ä―Ä –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è –Η –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –±―Ä–Ψ–Ι –Ψ―¹–Η –Ψ―² –±–Β–Ζ–Κ―Ä–Α–Β–Ϋ –Ω–Ψ―Ä―è–¥―ä–Κ –Η ―Ä–Α–≤–Ϋ–Η–Ϋ–Η –Ϋ–Α ―¹–Η–Φ–Β―²―Ä–Η―è). –û–Ω–Η―¹–≤–Α ―¹–Β –Ψ―² ―¹–Η–Φ–Β―²―Ä–Η―è―²–Α –Ϋ–Α –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Α –Ϋ–Β–Ω–Ψ–¥–≤–Η–Ε–Ϋ–Α ―¹―³–Β―Ä–Α. |
–‰–Ζ―Ä–Α–Ζ―è–≤–Α –Η–Ζ–Ψ―²―Ä–Ψ–Ω–Ϋ–Η (–Β–¥–Ϋ–Α–Κ–≤–Η, |
–£ ―΅–Β―²–Η―Ä–Η–Φ–Β―Ä–Ϋ–Ψ―²–Ψ –Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―¹―²–≤–Ψ, ―΅–Α―¹―²–Η―Ü–Η―²–Β –Ϋ–Α –Φ–Α―²–Β―Ä–Η―è―²–Α βÄ™¬†–Κ–≤–Α―Ä–Κ–Η¬†–Η¬†–Μ–Β–Ω―²–Ψ–Ϋ–Η ―¹–Β –Ψ–Ω–Η―¹–≤–Α―² –Ψ―² ―¹–Ω–Η–Ϋ–Ψ―Ä–Ϋ–Η –Ω–Ψ–Μ–Β―²–Α. –ü―Ä–Β–Ϋ–Ψ―¹–Η―²–Β–Μ–Η―²–Β –Ϋ–Α –Ζ–Α –≤–Ζ–Α–Η–Φ–Ψ–¥–Β–Ι―¹―²–≤–Η―è―²–Α - –±–Ψ–Ζ–Ψ–Ϋ–Η―²–Β: ―³–Ψ―²–Ψ–Ϋ–Η, –≥–Μ―É–Ψ–Ϋ–Η, W-–Η Z-–±–Ψ–Ζ–Ψ–Ϋ–Η –Ω―ä–Κ ―¹–Β –Ψ–Ω–Η―¹–≤–Α―² –Ψ―² –≤–Β–Κ―²–Ψ―Ä–Η. –Ξ–Η–≥―¹ –±–Ψ–Ζ–Ψ–Ϋ―ä―², –Κ–Ψ–Ι―²–Ψ –≤―¹–Β–Κ–Η –Φ–Ψ–Φ–Β–Ϋ―² ―â–Β –±―ä–¥–Β –Ψ―²–Κ―Ä–Η―², –Β ―¹–Κ–Α–Μ–Α―Ä. –Γ–Ω–Η–Ϋ–Ψ―Ä–Ϋ–Η―²–Β –Ω–Ψ–Μ–Β―²–Α, –Κ–Ψ–Η―²–Ψ –Ψ–Ω–Η―¹–≤–Α―² ―³―É–Ϋ–¥–Α–Φ–Β–Ϋ―²–Α–Μ–Ϋ–Α―²–Α –Φ–Α―²–Β―Ä–Η―è –Ω―Ä–Η―²–Β–Ε–Α–≤–Α―² –Φ–Ϋ–Ψ–≥–Ψ "―¹―²―Ä–Α–Ϋ–Ϋ–Α" ―¹–Η–Φ–Β―²―Ä–Η―è: –Ω―Ä–Η –Ω―ä–Μ–Ϋ–Ψ –Ζ–Α–≤―ä―Ä―²–Α–Ϋ–Β –Ϋ–Α 360 –≥―Ä–Α–¥―É―¹–Α ―¹–Ω–Η–Ϋ–Ψ―Ä–Ϋ–Ψ―²–Ψ –Ω–Ψ–Μ–Β –Ϋ–Β ―¹―ä–≤–Ω–Α–¥–Α ―¹―ä―¹ ―¹–Β–±–Β ―¹–Η.
–‰–Ζ―²–Ψ―΅–Ϋ–Η–Κ
Introduction to Group Theory, Dog School of Mathematics
Group theory, wikipedia
–Δ–Β–Ψ―Ä–Η―è –≥―Ä―É–Ω–Ω, wikipedia
Point_group, en.wikipedia
–û―¹–Ϋ–Ψ–≤–Ϋ―΄–Β –Ω–Ψ–Ϋ―è―²–Η―è ―²–Β–Ψ―Ä–Η–Η –≥―Ä―É–Ω–Ω –Η –Η―Ö –Ω―Ä–Β–¥―¹―²–Α–≤–Μ–Β–Ϋ–Η–Ι –Η¬†–Ϋ–Β–Κ–Ψ―²–Ψ―Ä―΄–Β –Ω―Ä–Η–Μ–Ψ–Ε–Β–Ϋ–Η―è –Κ ―³–Η–Ζ–Η–Κ–Β ―΅–Α―¹―²–Η―Ü, –£.–Γ. –½–Α–Φ–Η―Ä–Α–Μ–Ψ–≤
–û―¹–Ϋ–Ψ–≤–Η –Ϋ–Α –Φ–Η–Ϋ–Β―Ä–Α–Μ–Ψ–≥–Η―è―²–Α, ¬†–†―É―¹–Μ–Α–Ϋ –‰–≤–Α–Ϋ–Ψ–≤ –ö–Ψ―¹―²–Ψ–≤
–Δ–Β–Ϋ–Ζ–Ψ―Ä, ru.wikipedia
–ü―Ä–Β–¥–Β–Μ―¨–Ϋ―΄–Β –≥―Ä―É–Ω–Ω―΄ ―¹–Η–Φ–Φ–Β―²―Ä–Η–Η, –ë―Ä–Α–Ε–Β –†.–ê.
–ö–Ψ–Ϋ―Ü–Β–Ω―Ü–Η–Η ―¹–Ψ–≤―Ä–Β–Φ–Β–Ϋ–Ϋ–Ψ–≥–Ψ –Β―¹―²–Β―¹―²–≤–Ψ–Ζ–Ϋ–Α–Ϋ–Η―è. –€–Α―²–Β―Ä–Η–Α–Μ―΄ –Κ ―¹–Β–Φ–Η–Ϋ–Α―Ä―¹–Κ–Η–Φ –Ζ–Α–Ϋ―è―²–Η―è–Φ, –ë―Ä–Α–Ε–Β –†.–ê.
–ü―Ä–Β–¥–Β–Μ―¨–Ϋ―΄–Β –≥―Ä―É–Ω–Ω―΄ ―¹–Η–Φ–Φ–Β―²―Ä–Η–Η, –ë–Ψ–Μ―¨―à–Α―è ―ç–Ϋ―Ü–Η–Κ–Μ–Ψ–Ω–Β–¥–Η―è –ö–Η―Ä–Η–Μ–Μ–Α –Η –€–Β―³–Ψ–¥–Η―è
–Γ–Η–Φ–Β―²―Ä–Η―è¬†,¬†–Λ―É–Ϋ–¥–Α–Φ–Β–Ϋ―²–Α–Μ–Ϋ–Α –Λ–Η–Ζ–Η–Κ–Α,¬†–‰–Μ–Η―è –‰–Μ–Η–Β–≤
–≠–Μ–Β–Κ―²―Ä–Η―΅–Β―¹–Κ–Η–Β ―¹–≤–Ψ–Ι―¹―²–≤–Α –Κ―Ä–Η―¹―²–Α–Μ–Μ–Ψ–≤, –™–Ψ―Ä―è–Β–≤–Α –ê






















–ö–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
–€–Ψ–Μ―è, ―Ä–Β–≥–Η―¹―²―Ä–Η―Ä–Α–Ι―²–Β ―¹–Β –Ψ―² T–Θ–ö!
–ê–Κ–Ψ –≤–Β―΅–Β –Η–Φ–Α―²–Β ―Ä–Β–≥–Η―¹―²―Ä–Α―Ü–Η―è, –Ϋ–Α―²–Η―¹–Ϋ–Β―²–Β –Δ–Θ–ö!
–ù―è–Φ–Α –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η –Κ―ä–Φ ―²–Α–Ζ–Η –Ϋ–Ψ–≤–Η–Ϋ–Α !
–ü–Ψ―¹–Μ–Β–¥–Ϋ–Η –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
4I4ATA
–ù–Ψ–≤, ―¹–Κ―Ä–Η―² –¥–Ψ―¹–Β–≥–Α –≤―Ö–Ψ–¥ –≤ –Ω–Η―Ä–Α–Φ–Η–¥–Α―²–Α –Ϋ–Α –€–Η–Κ–Β―Ä–Η–Ϋ –Β –Ψ―²–Κ―Ä–Η―² –Ω–Ψ –Α–Ϋ–Ψ–Φ–Α–Μ–Η–Η –Ω―Ä–Η ―¹–Κ–Α–Ϋ–Η―Ä–Α–Ϋ–Β
YKoshev
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
Johnny B Goode
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
Gunteer
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews