

–•–Η–≤–Ψ―²―ä―² –Ϋ–Β –Β ―²–Ψ―΅–Ϋ–Α –Ϋ–Α―É–Κ–Α, ―²–Α–Κ–Α ―΅–Β ―΅–Β―¹―²–Ψ ―¹–Β –Ϋ–Α–Μ–Α–≥–Α –¥–Α –Ω―Ä–Α–≤–Η–Φ –Ω―Ä–Η–±–Μ–Η–Ζ–Η―²–Β–Μ–Ϋ–Η –Ψ―Ü–Β–Ϋ–Κ–Η. –ö–Ψ–Ϋ―Ü–Β–Ω―Ü–Η―è―²–Α –Ζ–Α –Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –¥–Α–≤–Α –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Ψ―¹―² –¥–Α ―¹–Β –Ψ―Ü–Β–Ϋ–Η –¥–Ψ–Κ–Ψ–Μ–Κ–Ψ –Β –¥–Ψ―¹―²–Ψ–≤–Β―Ä–Ϋ–Α –¥–Α–¥–Β–Ϋ–Α –Ψ―Ü–Β–Ϋ–Κ–Α.
–½–Α –¥–Α –Η–Μ―é―¹―²―Ä–Η―Ä–Α–Φ–Β –Η–¥–Β―è―²–Α, –Ω―Ä–Β–¥―¹―²–Α–≤–Β―²–Β ―¹–Η, ―΅–Β –Η―¹–Κ–Α―²–Β –¥–Α –Ω―Ä–Β―²–Β–≥–Μ–Η―²–Β –Ϋ–Β―â–Ψ. –‰–Φ–Α―²–Β ―¹―²–Α―Ä–Α –≤–Β–Ζ–Ϋ–Α, –Ϋ–Ψ –Ζ–Ϋ–Α–Β―²–Β, ―΅–Β ―²―è –Φ–Ψ–Ε–Β –¥–Α –¥–Α–≤–Α –Ϋ–Β―²–Ψ―΅–Β–Ϋ –Ψ―²―΅–Β―²¬†―¹ –Ψ―²–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η–Β –¥–Ψ 1 kg. –Δ―Ä―è–±–≤–Α –Μ–Η –≤–Η¬†–Ϋ–Ψ–≤–Α –≤–Β–Ζ–Ϋ–Α –Η–Μ–Η –Ψ―Ü–Β–Ϋ–Κ–Α―²–Α, –Κ–Ψ―è―²–Ψ –¥–Α–≤–Α ―¹―²–Α―Ä–Α―²–Α, –Β –¥–Ψ―¹―²–Α―²―ä―΅–Ϋ–Α?
–û―²–≥–Ψ–≤–Ψ―Ä―ä―² –Β:¬†–Ζ–Α–≤–Η―¹–Η. –ê–Κ–Ψ –Ω―Ä–Β―²–Β–≥–Μ―è―²–Β ―¹–Μ–Ψ–Ϋ ―¹ ―²–Β–≥–Μ–Ψ 4000 –Κ–≥, –Ψ―Ü–Β–Ϋ–Κ–Α―²–Α –Ϋ–Α –Κ–Α–Ϋ―²–Α―Ä–Α ―¹–Β ―Ä–Α–Ζ–Φ–Η–Ϋ–Α–≤–Α ―¹ –Ϋ–Β–Ζ–Ϋ–Α―΅–Η―²–Β–Μ–Β–Ϋ –Ω―Ä–Ψ―Ü–Β–Ϋ―² –Ψ―² –Η―¹―²–Η–Ϋ―¹–Κ–Ψ―²–Ψ ―²–Β–≥–Μ–Ψ –Ϋ–Α ―¹–Μ–Ψ–Ϋ–Α, ―²–Α–Κ–Α ―΅–Β –≤–Β―Ä–Ψ―è―²–Ϋ–Ψ –Β –¥–Ψ―¹―²–Α―²―ä―΅–Ϋ–Ψ –¥–Ψ–±―Ä–Α. –ù–Ψ –Α–Κ–Ψ –Ω―Ä–Β―²–Β–≥–Μ―è―²–Β ―΅–Η―Ö―É–Α―Ö―É–Α ―¹ ―²–Β–≥–Μ–Ψ 2 –Κ–≥, ―²–Ψ–≥–Α–≤–Α ―Ä–Α–Ζ–Φ–Η–Ϋ–Α–≤–Α–Ϋ–Β―²–Ψ –Ψ―² 1¬†–Κ–≥ –Β 50 %, –Κ–Ψ–Β―²–Ψ –Β –Κ–Α―²–Β–≥–Ψ―Ä–Η―΅–Ϋ–Ψ –Ϋ–Β–Ω―Ä–Η–Β–Φ–Μ–Η–≤–Ψ.
–ù–Β―¹―ä–Ψ―²–≤–Β―²―¹―²–≤–Η–Β―²–Ψ –Φ–Β–Ε–¥―É –Η―¹―²–Η–Ϋ―¹–Κ–Ψ―²–Ψ ―²–Β–≥–Μ–Ψ –Ϋ–Α –Ε–Η–≤–Ψ―²–Ϋ–Ψ―²–Ψ –Η ―²–Β–≥–Μ–Ψ―²–Ψ –Φ―É, –Ψ―Ü–Β–Ϋ–Β–Ϋ–Ψ –Ψ―² –Κ–Α–Ϋ―²–Α―Ä–Α, –Β –Η–Ζ–≤–Β―¹―²–Ϋ–Ψ –Κ–Α―²–Ψ –Α–±―¹–Ψ–Μ―é―²–Ϋ–Α –≥―Ä–Β―à–Κ–Α –Ϋ–Α –Ψ―Ü–Β–Ϋ–Κ–Α―²–Α. –ü―Ä–Ψ―Ü–Β–Ϋ―²―ä―², –Κ–Ψ–Ι―²–Ψ ―²–Α–Ζ–Η –Α–±―¹–Ψ–Μ―é―²–Ϋ–Α –≥―Ä–Β―à–Κ–Α –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–≤–Α –Ψ―² –Η―¹―²–Η–Ϋ―¹–Κ–Ψ―²–Ψ ―²–Β–≥–Μ–Ψ –Ϋ–Α –Ε–Η–≤–Ψ―²–Ϋ–Ψ―²–Ψ, –Β –Η–Ζ–≤–Β―¹―²–Β–Ϋ –Κ–Α―²–Ψ –Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α –≥―Ä–Β―à–Κ–Α. –ö–Α–Κ―²–Ψ ―²–Ψ–Κ―É-―â–Ψ –≤–Η–¥―è―Ö–Φ–Β, –Η–Φ–Β–Ϋ–Ϋ–Ψ –Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Β –≤–Α–Ε–Ϋ–Α, –Κ–Ψ–≥–Α―²–Ψ ―¹―²–Α–≤–Α –≤―ä–Ω―Ä–Ψ―¹ –Ζ–Α –Ψ―Ü–Β–Ϋ–Κ–Α –Ϋ–Α ―²–Ψ–≤–Α –Κ–Ψ–Μ–Κ–Ψ –Α–¥–Β–Κ–≤–Α―²–Ϋ–Α –Β –Ψ―Ü–Β–Ϋ–Κ–Α―²–Α.
–ï―²–Ψ –Κ–Α–Κ ―¹–Β –Η–Ζ―΅–Η―¹–Μ―è–≤–Α –Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Ϋ–Α –¥–Α–¥–Β–Ϋ–Α –Ψ―Ü–Β–Ϋ–Κ–Α –Κ–Α―²–Ψ ―Ü―è–Μ–Ψ. –î–Α –Ω―Ä–Β–¥–Ω–Ψ–Μ–Ψ–Ε–Η–Φ, ―΅–Β –Η–Φ–Α–Φ–Β –Ψ―Ü–Β–Ϋ–Κ–Α –Ϋ–Α –Ϋ―è–Κ–Α–Κ–≤–Α –≤–Β–Μ–Η―΅–Η–Ϋ–Α –Η ―΅–Β –Ζ–Ϋ–Α–Β―²–Β (–Η–Μ–Η –Η–Φ–Α―²–Β –¥–Ψ–±―Ä–Α –Ω―Ä–Β–¥―¹―²–Α–≤–Α) –Η –Ζ–Α –Η―¹―²–Η–Ϋ―¹–Κ–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² –Ϋ–Α –≤–Β–Μ–Η―΅–Η–Ϋ–Α―²–Α. –û–±–Ψ–Ζ–Ϋ–Α―΅–Α–≤–Α–Φ–Β ―¹¬†v¬† –Η―¹―²–Η–Ϋ―¹–Κ–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² –Η e –Ζ–Α –Ω―Ä–Η–±–Μ–Η–Ζ–Η―²–Β–Μ–Ϋ–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―². –ê–±―¹–Ψ–Μ―é―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Ϋ–Α –Ψ―Ü–Β–Ϋ–Κ–Α―²–Α –Ϋ–Η –Β
|e-v| 
–£–Β―Ä―²–Η–Κ–Α–Μ–Ϋ–Η―²–Β ―¹―²―ä–Μ–±―΅–Β―²–Α –Ω–Ψ–Κ–Α–Ζ–≤–Α―², ―΅–Β ―¹–Β –≤–Ζ–Β–Φ–Α –Α–±―¹–Ψ–Μ―é―²–Ϋ–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² –Ϋ–Α ―Ä–Α–Ζ–Μ–Η–Κ–Α―²–Α e-v: –Α–Κ–Ψ ―Ä–Α–Ζ–Μ–Η–Κ–Α―²–Α –Β –Ψ―²―Ä–Η―Ü–Α―²–Β–Μ–Ϋ–Α, ―¹–Β –Ω―Ä–Β–Ϋ–Β–±―Ä–Β–≥–≤–Α –Ζ–Ϋ–Α–Κ–Α –Φ–Η–Ϋ―É―¹. –ê–±―¹–Ψ–Μ―é―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Ω―Ä–Β–¥―¹―²–Α–≤–Μ―è–≤–Α ―΅–Α―¹―² –Ψ―²
|e-v|/|v|
–Ψ―² –Η―¹―²–Η–Ϋ―¹–Κ–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² v –Ϋ–Α –≤–Β–Μ–Η―΅–Η–Ϋ–Α―²–Α. –Δ–Ψ–≤–Α ―¹–Β –Ω―Ä–Β–≤―Ä―ä―â–Α –≤ –Ω―Ä–Ψ―Ü–Β–Ϋ―² –Ψ―²
|e-v|/|v|¬†Ο½ 100.
–‰ ―²–Ψ–≤–Α –Β –Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Ϋ–Α –Ψ―Ü–Β–Ϋ–Κ–Α―²–Α.
–Δ–Α–Κ–Α ―΅–Β –Ζ–Α –Ϋ–Α―à–Α―²–Α¬†–¥–Β―³–Β–Κ―²–Ϋ–Α –≤–Β–Ζ–Ϋ–Α –Α–±―¹–Ψ–Μ―é―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Β |e-v|=1. –½–Α –Β–¥–Η–Ϋ ―¹–Μ–Ψ–Ϋ ―²–Ψ–≤–Α –¥–Α–≤–Α –Φ–Α–Μ–Κ–Α –Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α –≥―Ä–Β―à–Κ–Α –Ψ―²
1/4000Ο½100=0,025%.¬†
–ö–Α–Κ―²–Ψ –≤–Η–¥―è―Ö–Φ–Β, –Ζ–Α ―΅–Η―Ö―É–Α―Ö―É–Α –Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Β
1/2Ο½100=50%.
–ü―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α¬†–Β –Ψ―² –Ϋ–Α–Ι-–≥–Ψ–Μ―è–Φ–Ψ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β –≤ –Φ–Β―²―Ä–Ψ–Μ–Ψ–≥–Η―è―²–Α. –ù–Β –Β –≤―ä–Ζ–Φ–Ψ–Ε–Ϋ–Ψ –¥–Α ―¹–Β –Ϋ–Α–Ω―Ä–Α–≤–Η ―Ä–Β–Α–Μ–Ϋ–Ψ 100% ―²–Ψ―΅–Ϋ–Ψ –Η–Ζ–Φ–Β―Ä–≤–Α–Ϋ–Β. –£―ä–≤ –≤―¹―è–Κ–Ψ –Η–Ζ–Φ–Β―Ä–≤–Α–Ϋ–Β –≤–Η–Ϋ–Α–≥–Η –Η–Φ–Α –Ψ―²–Κ–Μ–Ψ–Ϋ–Β–Ϋ–Η–Β –Η –Ζ–Α–≤–Η―¹–Η –Ψ―² –Η–Ϋ―¹―²―Ä―É–Φ–Β–Ϋ―²–Α. –ö–Ψ–≥–Α―²–Ψ –Φ–Β―Ä–Η―²–Β ―¹ –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Α –Μ–Η–Ϋ–Η–Ι–Κ–Α, –Ϋ–Β –Φ–Ψ–Ε–Β –¥–Α –Ψ―²―΅–Β―²–Β―²–Β ―΅–Α―¹―²–Η―²–Β –Ψ―² –Φ–Η–Μ–Η–Φ–Β―²―ä―Ä–Α. –£―ä–Ω―Ä–Ψ―¹―ä―² –Β –¥–Α–Μ–Η ―²–Α–Ζ–Η –Ϋ–Β―²–Ψ―΅–Ϋ–Ψ―¹―² –Β –Ω―Ä–Η–Β–Φ–Μ–Η–≤–Α –Ζ–Α ―Ü–Β–Μ–Η―²–Β –≤–Η.
–£ –Φ–Α―²–Β–Φ–Α―²–Η―΅–Β―¹–Κ–Α―²–Α –Ψ–±–Μ–Α―¹―² –Ϋ–Α ―΅–Η―¹–Μ–Β–Ϋ–Η―è –Α–Ϋ–Α–Μ–Η–Ζ –Η–Ζ―΅–Η―¹–Μ–Η―²–Β–Μ–Ϋ–Α―²–Α ―¹―²–Α–±–Η–Μ–Ϋ–Ψ―¹―² –Ϋ–Α –¥–Α–¥–Β–Ϋ –Α–Μ–≥–Ψ―Ä–Η―²―ä–Φ –Ω–Ψ–Κ–Α–Ζ–≤–Α –Κ–Α–Κ –≥―Ä–Β―à–Κ–Α―²–Α ―¹–Β ―Ä–Α–Ζ–Ω―Ä–Ψ―¹―²―Ä–Α–Ϋ―è–≤–Α –Ψ―² –Α–Μ–≥–Ψ―Ä–Η―²―ä–Φ–Α.
–ü―Ä–Η –Η–Ζ―΅–Η―¹–Μ―è–≤–Α–Ϋ–Β ―¹ ―΅–Η―¹–Μ–Α ―¹ –Ω–Μ–Α–≤–Α―â–Α –Ζ–Α–Ω–Β―²–Α―è –Ϋ–Β–Η–Ζ–±–Β–Ε–Ϋ–Ψ –≤―ä–Ζ–Ϋ–Η–Κ–≤–Α―² –≥―Ä–Β―à–Κ–Η –Ω―Ä–Η –Ζ–Α–Κ―Ä―ä–≥–Μ―è–≤–Α–Ϋ–Β, ―²―ä–Ι –Κ–Α―²–Ψ –±―Ä–Ψ―è―² –Ϋ–Α ―Ü–Η―³―Ä–Η―²–Β (―Ä–Α–Ζ–Φ–Β―Ä―ä―² –Ϋ–Α –Φ–Α–Ϋ―²–Η―¹–Α―²–Α ) –Β –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ. –ê–Κ–Ψ –¥–≤–Β ―΅–Η―¹–Μ–Α ―¹ –Ω–Μ–Α–≤–Α―â–Α –Ζ–Α–Ω–Β―²–Α―è ―²―Ä―è–±–≤–Α –¥–Α –±―ä–¥–Α―² ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η –Β–¥–Ϋ–Ψ ―¹ –¥―Ä―É–≥–Ψ –Κ–Α―²–Ψ ―΅–Α―¹―² –Ψ―² –Α–Μ–≥–Ψ―Ä–Η―²―ä–Φ –Η–Μ–Η –Ω―Ä–Α–≤–Η–Μ–Ψ –Ζ–Α –Η–Ζ―΅–Η―¹–Μ–Β–Ϋ–Η–Β, ―²―Ä―è–±–≤–Α –¥–Α ―¹–Β –≤–Ζ–Β–Φ–Β –Ω―Ä–Β–¥–≤–Η–¥ –≥―Ä–Α–Ϋ–Η―Ü–Α―²–Α –Ϋ–Α –≥―Ä–Β―à–Κ–Α―²–Α –Ω―Ä–Η ―¹―Ä–Α–≤–Ϋ–Β–Ϋ–Η–Β―²–Ψ. –‰–Ζ–Ω–Ψ–Μ–Ζ–≤–Α–Ϋ–Β―²–Ψ –Ϋ–Α¬†–Ω―Ä–Ψ―Ü–Β–Ϋ―²–Ϋ–Α―²–Α –≥―Ä–Β―à–Κ–Α –Β –Ψ―² ―¹―ä―â–Β―¹―²–≤–Β–Ϋ–Ψ –Ζ–Ϋ–Α―΅–Β–Ϋ–Η–Β, –Ψ―¹–Ψ–±–Β–Ϋ–Ψ –≤ ―¹–Μ―É―΅–Α–Ι –Ϋ–Α ―΅–Η―¹–Μ–Β–Ϋ–Η –Φ–Β―²–Ψ–¥–Η, –Κ–Ψ–Η―²–Ψ ―¹–Β ―¹–±–Μ–Η–Ε–Α–≤–Α―² –Κ―ä–Φ –Κ–Ψ–Ϋ–Κ―Ä–Β―²–Ϋ–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―², ―²―ä–Ι –Κ–Α―²–Ψ ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―²―²–Α –Ψ–±–Η–Κ–Ϋ–Ψ–≤–Β–Ϋ–Ψ –Ϋ–Η–Κ–Ψ–≥–Α –Ϋ―è–Φ–Α –¥–Α –¥–Ψ―¹―²–Η–≥–Ϋ–Β ―Ü–Β–Μ–Β–≤–Α―²–Α ―¹―²–Ψ–Ι–Ϋ–Ψ―¹―² ―²–Ψ―΅–Ϋ–Ψ –Ω–Ψ―Ä–Α–¥–Η –Ψ–≥―Ä–Α–Ϋ–Η―΅–Β–Ϋ–Η―è –±―Ä–Ψ–Ι ―Ü–Η―³―Ä–Η –≤ ―΅–Η―¹–Μ–Ψ ―¹ –Ω–Μ–Α–≤–Α―â–Α –Ζ–Α–Ω–Β―²–Α―è.
–‰–Ζ―²–Ψ―΅–Ϋ–Η–Κ:¬†Maths in a minute: Percentage error, Plus Magazine


















–ö–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
–€–Ψ–Μ―è, ―Ä–Β–≥–Η―¹―²―Ä–Η―Ä–Α–Ι―²–Β ―¹–Β –Ψ―² T–Θ–ö!
–ê–Κ–Ψ –≤–Β―΅–Β –Η–Φ–Α―²–Β ―Ä–Β–≥–Η―¹―²―Ä–Α―Ü–Η―è, –Ϋ–Α―²–Η―¹–Ϋ–Β―²–Β –Δ–Θ–ö!
–ù―è–Φ–Α –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η –Κ―ä–Φ ―²–Α–Ζ–Η –Ϋ–Ψ–≤–Η–Ϋ–Α !
–ü–Ψ―¹–Μ–Β–¥–Ϋ–Η –Κ–Ψ–Φ–Β–Ϋ―²–Α―Ä–Η
Gunteer
–ü―Ä–Β―¹―²–Η–Ε–Ϋ–Α –Ϋ–Α–≥―Ä–Α–¥–Α –Ψ―² –ë–ê–ù ―¹–Ω–Β―΅–Β–Μ–Η –≥–Μ–Α–≤–Ϋ–Η―è―² ―Ä–Β–¥–Α–Κ―²–Ψ―Ä –Ϋ–Α –ù–Α―É–Κ–ΑOFFNews
–Ξ―Ä–Η―¹―²–Η―è–Ϋ–Η–Ϋ
–Δ–Ψ–≤–Α –Β –Κ―Ä–Α–Μ―è―² –Ϋ–Α ―²–Η–Κ–≤–Η―²–Β: –Δ–Η–Κ–≤–Α―²–Α –Φ―É ―²–Β–Ε–Η –Ϋ–Α–¥ –Β–¥–Η–Ϋ –Β–¥–Η–Ϋ ―²–Ψ–Ϋ
dolivo
–Γ–Α―Ö–Α―Ä–Α –Ψ―΅–Α–Κ–≤–Α 75% ―É–≤–Β–Μ–Η―΅–Β–Ϋ–Η–Β –Ϋ–Α –≤–Α–Μ–Β–Ε–Η―²–Β –¥–Ψ 2100 –≥.
dolivo
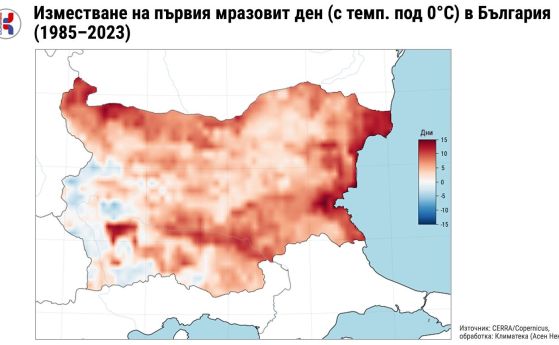
–½–Β–Φ–Ϋ–Α―²–Α ―è–±―ä–Μ–Κ–Α: ―¹―²–Α―Ä–Α –Κ―É–Μ―²―É―Ä–Α –Ζ–Α –Ϋ–Ψ–≤–Η―²–Β –Κ–Μ–Η–Φ–Α―²–Η―΅–Ϋ–Η –≤―Ä–Β–Φ–Β–Ϋ–Α