
Тригонометрията е клон на математиката, който изучава триъгълниците и по-специално - връзките между ъглите и дължините на съответните страни.
Интересно е, че тригонометричните функции, които определят тези взаимоотношения, са тясно свързани с окръжността.
Излишно е да се каже, това прави една от най-трудните теми в математиката за учениците, но тя може да се разбере интуитивно и това е част от начина, по който се преподава. Учениците се обучават за връзката на кръга с тригонометрия, но мнозина не успяват да остзнаят дълбочината на тази връзка.
Със статични графики и уравнения е възможно да се справите с правилата какво означават различните функции, но определено е по-лесно с анимирани GIF-ове, защото се добавя още едно измерение - времето. Как се променят тригонометричните функции с течение на времето е от решаващо значение за разбирането им.
Изданието Business Insider представя подбор от анимирани тригонометрични GIF-ове.
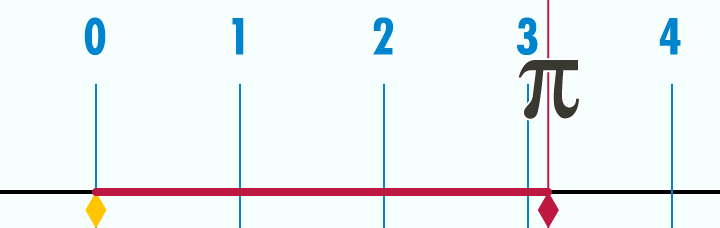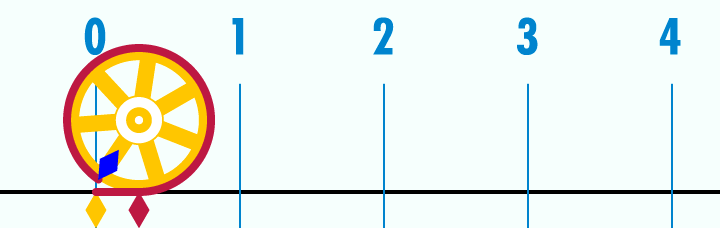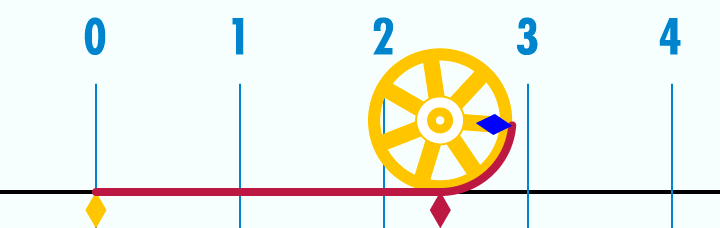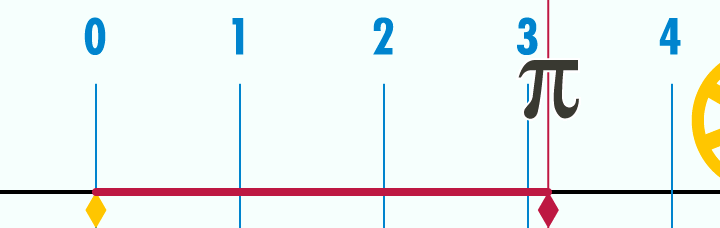
За начало ето какво представлява числото π:
А ето как може да лесно може да се разбере какво са радианите:
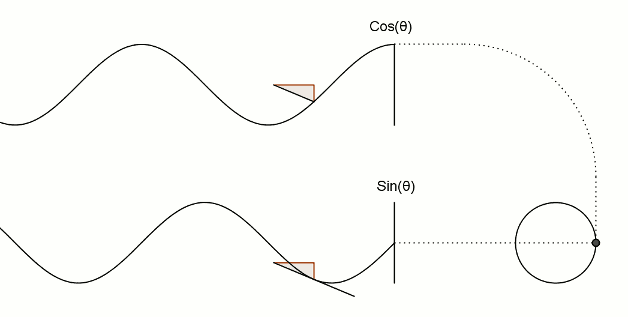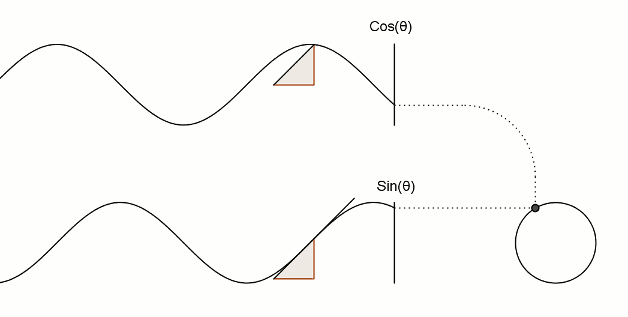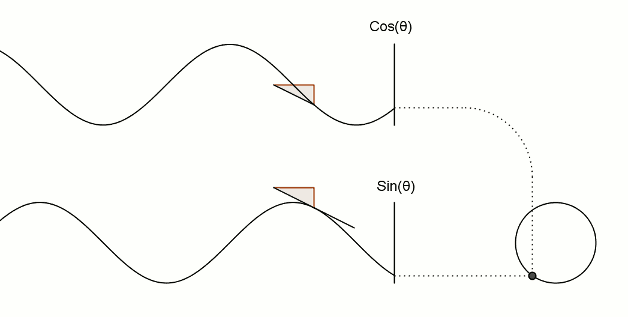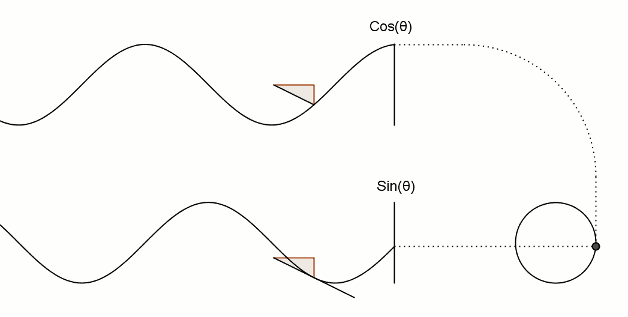
Сега да видим връзката между синусите, косинуса и кръга. Ето илюстрация на основните взаимоотношения между трите.
Забележете как манивелата се движи в кръг, а плъзгачите, които съответстват на синуса и косинуса, се движат нагоре-надолу във вълнообразна форма:
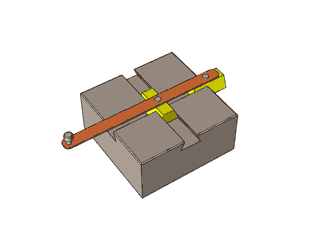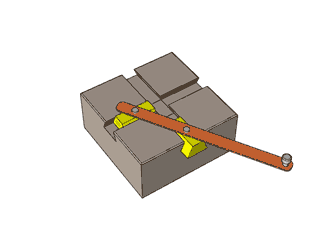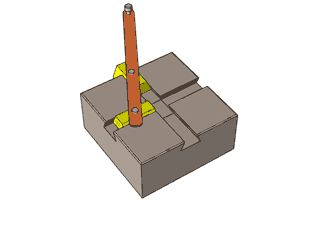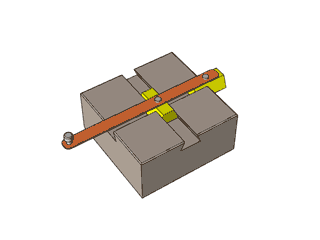
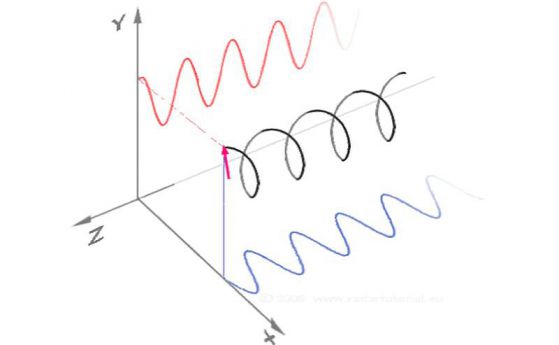
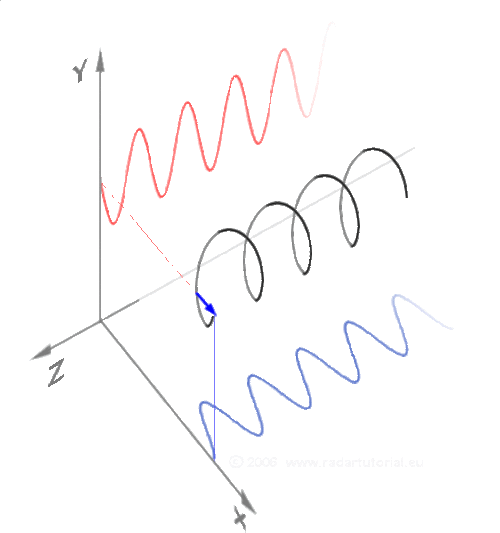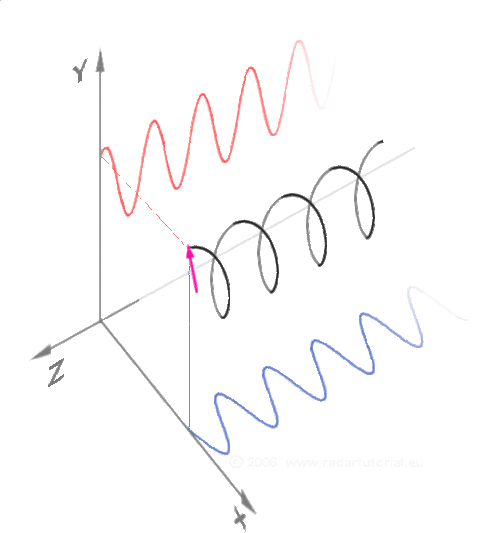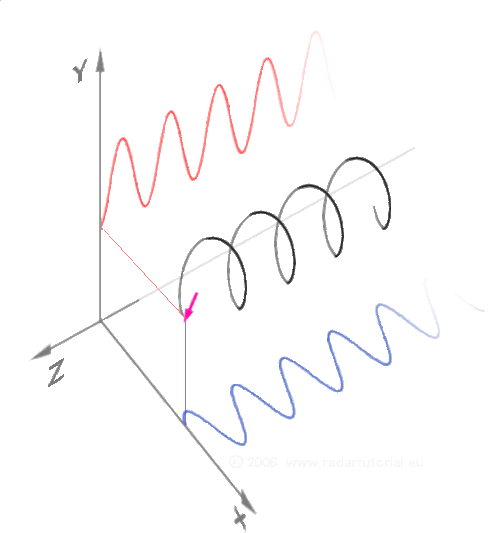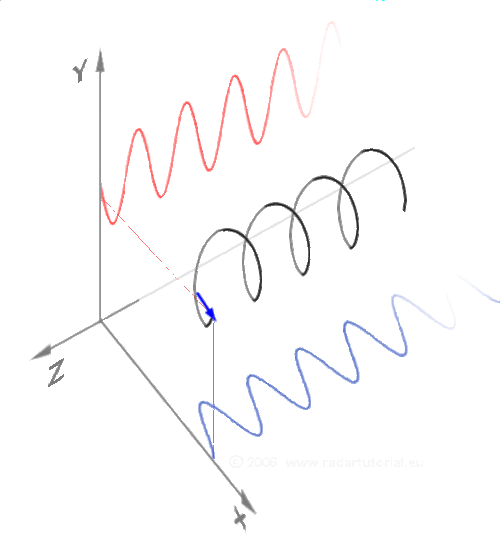
Ето една по-традиционна демонстрация на синус и косинус. Черна точка едновременно обикаля в кръг и по оста Z. По този начин стойностите по Y се трансформират на синусоида (червената линия) и стойностите по X се трансформират на косинусоида (синя линия):
Сега можем да свържем тази връзка между функциите и кръговете с триъгълници:
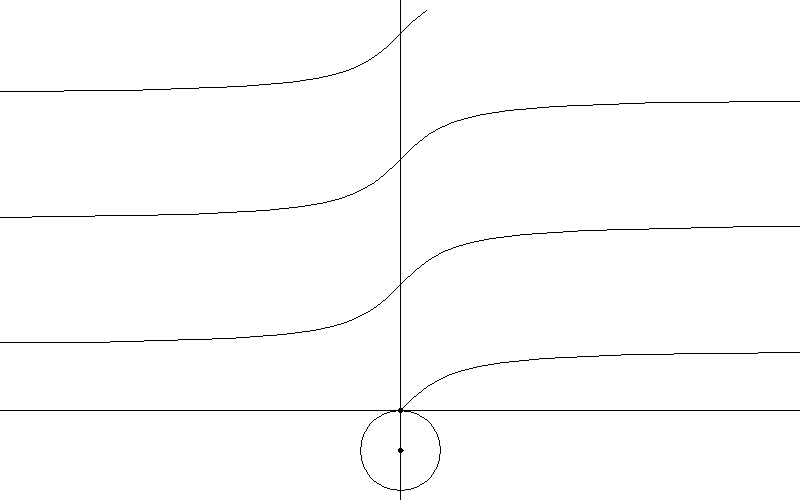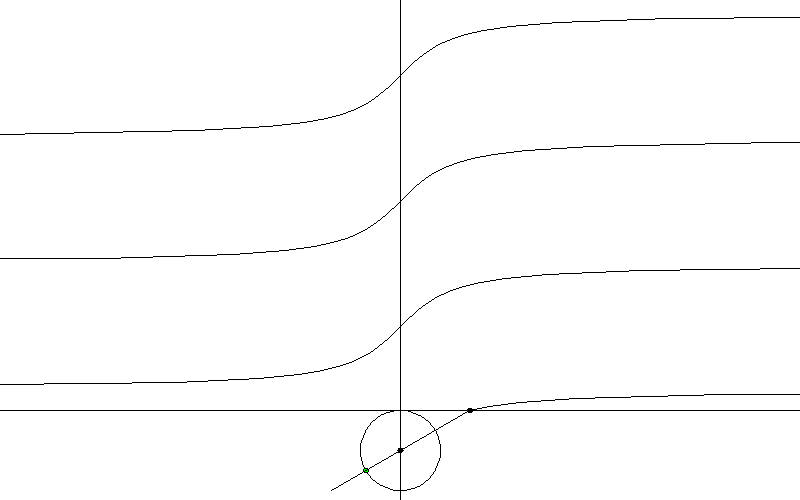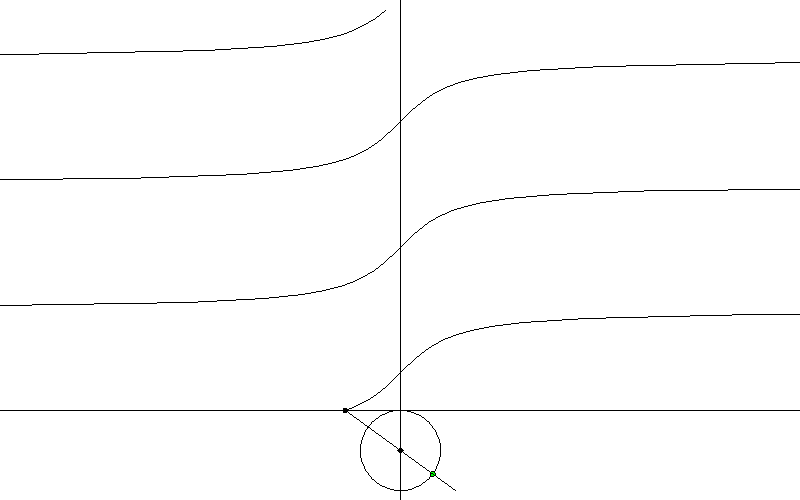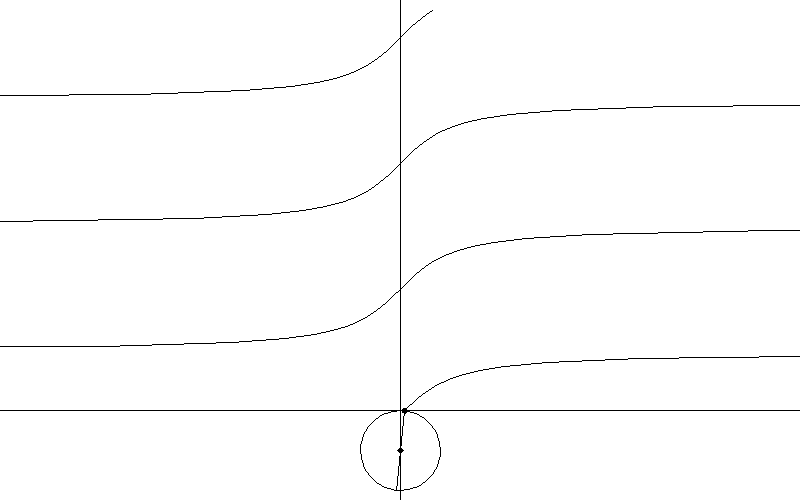
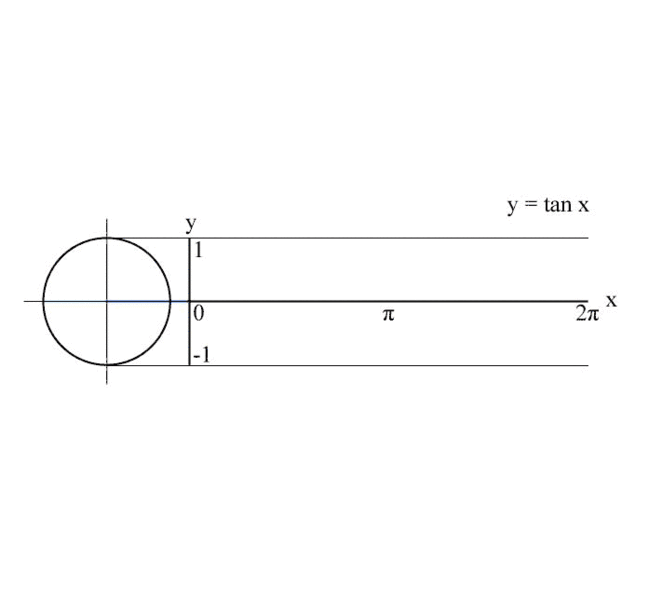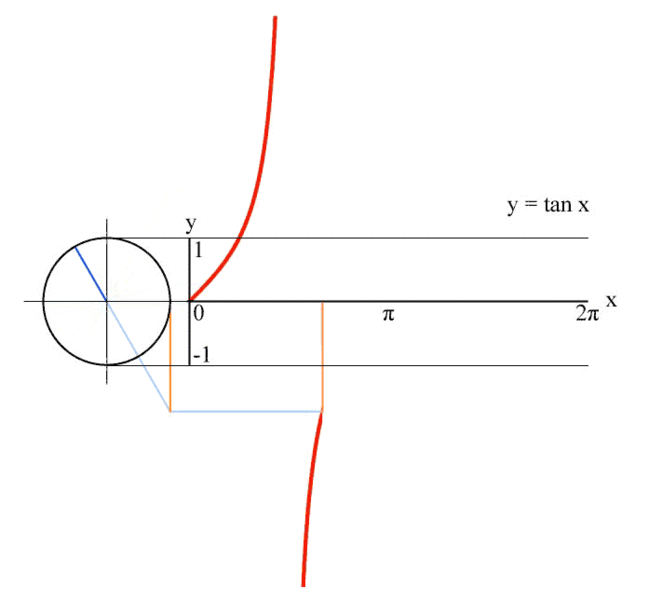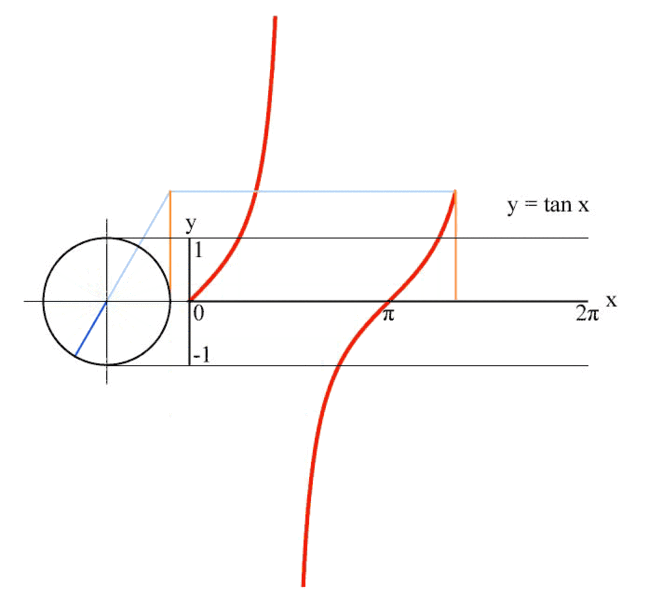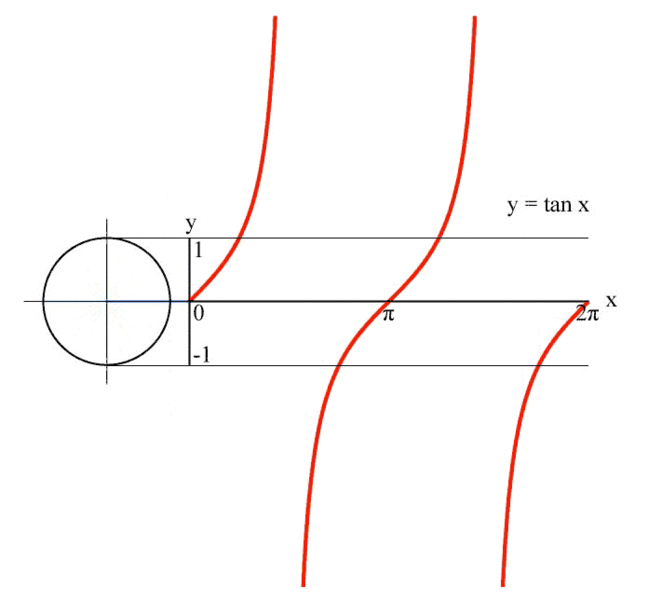
Връзката на триъгълника е от решаващо значение за дефинирането на функцията тангенс - tan(). Пресечната точка на линията на хипотенузата на триъгълника с вертикалната линия от дясната страна на кръга определя функцията.
Друг начин да се покаже без триъгълник:





















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
4I4ATA
Нов, скрит досега вход в пирамидата на Микерин е открит по аномалии при сканиране
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews