
Много хора смятат, че математиката е човешко изобретение. За тях този начин на мислене математиката е като език - математиката може да описва реални неща в света около нас, но не „съществува” извън умовете на хората, които я използват.
Но според питагорейската философска школа в древна Гърция реалността в основата си е математическа.
Повече от 2000 години по-късно философи и физици започват да приемат сериозно тази идея.
Една нова статия на доцент Сам Барън (Sam Baron) от Австралийския католически университет твърди, че математиката е основен компонент на природата, който придава структура на физическия свят.
Пчелите решават задача за математическа оптимизация: отговорът е "шестоъгълници"
Пчелите в кошерите произвеждат пчелни пити на шестоъгълници. Защо?
Шестоъгълниците са най-ефективната форма за облицовка на равнината. За да се покрие напълно повърхност с плочки с еднаква форма и размер, като същевременно общата дължина на периметърите им е минимална, фигурата, която трябва да се използва е шестоъгълник.
Чарлз Дарвин смята, че пчелите са еволюирали, за да използват тази форма, тъй като тя произвежда най-големите клетки за съхранение на мед с най-малко количество енергия за производство на восък.
Хипотезата за пчелна пита е предложена за първи път в древни времена, но е доказана едва през 1999 г. от математика Томас Хейлс.
 Кредит: Piqsels
Кредит: Piqsels
Математическата оптимизация е селекцията на най-добрия елемент според определен критерий - в случая максимално оградено пространство върху плоскост с използване на минимум материал. Шестоъгълниците са решение на тази задача, поставена не само пред пчелите - природата също е пестелива:
Дисипацията (разсейването) на енергия в течности зависи от отношенето на площта на клетката към обема й (специфичната повърхност): колкото е по-малко това отношение, толкова е по-малка дисипацията. Не е трудно да се убедим, че с най-малката специфичната повърхност се характеризира именно шестостенната клетка. С други думи, в пълно съответствие с изложените принципи, в експеримента на Бенар се реализира наи-изгодната енергийно конфигурация на клетките.
 |
 |
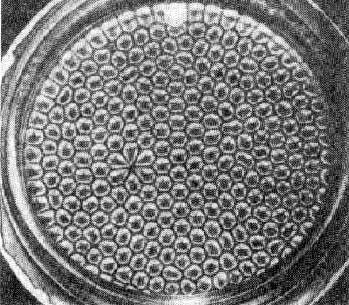
| При нагряване отдолу на слой живак в плосък широк съд, слоят се разпада на еднакви вертикални шестостенни призми, наречени клетки на Бенар. | Аналози на клетките на Бенар в стълбчатите шестостенни структури при базалти и гранити. Това са "подредени структури", които спонтанно се образуват в неравновесна среда. Такива структури се наричат дисипативни структури от фр. dissipation – разсейване. |
|
Дисипацията (разсейването) на енергия в течности зависи от отношенето на площта на клетката към обема й (специфичната повърхност): колкото е по-малко това отношение, толкова е по-малка дисипацията. Не е трудно да се убедим, че с най-малката специфичната повърхност се характеризира именно шестостенната клетка. С други думи, в пълно съответствие с изложените принципи, в експеримента на Бенар се реализира наи-изгодната енергийно конфигурация на клетките. |
|
Цикади и прости числа
Сам Барън привежда още един пример. Периодичните цикади (Magicicada) са род цикади, обитаващи източната част на Северна Америка. Тези насекоми имат изненадващо дълъг жизнен цикъл, с продължителност 13 или 17 години в зависимост от подвида си. Те прекарват по-голямата част от живота си в почвата и се появяват на големи рояци за период от около две седмици.
Но защо са 13 и 17 години? Защо не 12 и 14? Или 16 и 18?
Съществува хипотеза, че продължителността на циклите на повечето цикади не е случайна, а представлява интервали от прости числа (числа, делими без остатък само на себе си -.. 3, 5, 7, 11, 13, 17 и така нататък) и че това е най-ефективната стратегия за оцеляване и размножаване.
Проучванията показват, че числеността на животните, които се хранят с цикади - обикновено птици, паяци, оси, богомолки, риби и змии - често има по-кратък цикъл от 2-6 години между пика и спада на популацията. Ако цикадите се появяваха, например, на всеки 12 години, то всеки хищник с жизнения цикъл 2, 3, 4 или 6 години може да синхронизира циклите си на възход на числеността си с редовната поява на цикадите.
Такъв жизнен цикъл позволява на цикадите "да се разминат" не само с хищниците, но и със своите роднини, които имат различна продължителност на жизнения цикъл. Може би, ако различните видове цикади се появяваха едновременно, това щеше да доведе до близковидово кръстосване и появата на потомство с нередовен цикъл.
 Кредит: Sam Baron
Кредит: Sam Baron
Вижте графиката по-горе: P1–P9 представляват циклични хищници. Числовата права представлява години. Подчертаните пропуски показват как 13 и 17-годишните цикади успяват да избегнат своите хищници.
Ако сравните 13-годишен жизнен цикъл и 12-годишен жизнен цикъл, ще видите, че когато цикада с 12-годишен жизнен цикъл излезе на повърхността, 2-годишните, 3-годишните и 4-годишните хищници също ще бъдат заплаха, защото 2, 3 и 4 всички делят 12 без остатък.
Когато цикада с 13-годишен жизнен цикъл излезе от почвата, никой от нейните хищници няма да бъде готов за нападение, защото нито едното от числата 2, 3, 4, 5, 6, 7, 8 или 9 не дели без остатък 13. Същото важи и за 17.
Изглежда, че цикадите са еволюирали, за да използват основни факти за числата.
Създаваме или откриваме математиката?
Ако търсим, лесно ще намерим други примери. От формата на сапунените мехури до местоположението и размера на пролуките в пръстените на Сатурн, математиката е навсякъде.

Ако математиката обяснява толкова много неща, които виждаме около нас, тогава е малко вероятно математиката да е нещо, което сме създали. Алтернативата е, че математическите факти се откриват не само от хората, но и от насекоми, сапунени мехурчета и планети.
Какво е мислил Платон?
Но ако откриваме нещо, какво е то?
Отговорът на древногръцкия философ Платон е, че математиката описва обекти, които наистина съществуват. За Платон тези обекти са числа и геометрични фигури. Днес бихме могли да добавим по-сложни математически обекти като групи, категории, функции, полета и др. към списъка.
Платон смята, че математическите обекти съществуват извън пространството и времето. Но такъв възглед само задълбочава мистерията как математиката обяснява нещата.
Обяснението се състои в това, как едно нещо в света зависи от друго. Ако математическите обекти съществуват в област, различна от света, в който живеем, как тези математически обекти ще се свържат с нещо физическо?
 За Платон числата съществуват в сфера, отделена от физическия свят. Кредит: Geralt / Pixabay
За Платон числата съществуват в сфера, отделена от физическия свят. Кредит: Geralt / Pixabay
Барън въвежда питагорейството
Древните питагорейци са били съгласни с Платон, че математиката описва свят от обекти. Но за разлика от Платон, те не смятат, че математическите обекти съществуват извън пространството и времето, а че физическата реалност е изградена от математически обекти по същия начин, както материята е направена от атоми.
Ако реалността е направена от математически обекти, лесно е да се види как математиката може да играе роля в обяснението на света около нас.
През последното десетилетие двама физици изграждат солидна защита на питагорейската позиция: шведско-американският космолог Макс Тегмарк (Max Tegmark) и австралийският физик-философ Джейн Макдонъл (Jane McDonnell), разказва Сам Барън.
Тегмарк твърди, че реалността е просто един голям математически обект. Ако това изглежда странно, помислете за идеята, че реалността е симулация. Симулацията е компютърна програма, която е вид математически обект.
Погледът на Макдонъл е по-радикален. Тя смята, че реалността е съставена от математически обекти и разум. Математиката е начинът, по който Вселената, която е съзнателна, опознава себе си.
Сам Барън защитава различен възглед - светът се състои от две части, математика и материя. Математиката дава на материята нейната форма, а материята дава на математиката нейната същност.
Математическите обекти осигуряват структурна рамка за физическия свят.
Бъдещето на математиката
Логично е, че питагорейството се преоткрива във физиката.
През миналия век физиката стана все по-математическа, обръщайки се към привидно абстрактни области на изследване като теория на групите и диференциална геометрия в опит да обясни физическия свят.
"Тъй като границата между физика и математика се размива, става по-трудно да се каже кои части на света са физически и кои са математически. Но е странно, че питагорейството е било пренебрегвано от философите толкова дълго. Вярвам, че това е на път да се промени. Дойде времето за питагорейска революция, която обещава да промени радикално нашето разбиране за реалността", заключава Сам Барън.
Сам Барън е доцент от Австралийския католически университет.
Тази статия е препубликувана от The Conversation под лиценз Creative Commons. Прочетете оригиналната статия.
Справка: Mathematical Explanation: A Pythagorean Proposal
Samuel Baron
British Journal for the Philosophy of Science, https://www.journals.uchicago.edu/doi/pdf/10.1086/716181





















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон
dolivo
Сахара очаква 75% увеличение на валежите до 2100 г.
dolivo
Земната ябълка: стара култура за новите климатични времена