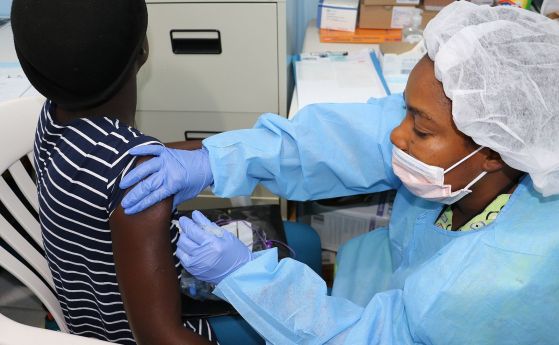
Преди 80 г. най-удачният междупланетен превоз е изглеждал снарядът, изстрелян от оръдие
В два от най-известните романи, писани през ХІХ век и посветени на космически пътешествия или междупланетни контакти ("От Земята до Луната" на Жюл Верн и "Война на световете" на Х. Уелс) пътуванията се извършват в големи снаряди (прожектили), изстреляни от топове и впоследствие движещи се свободно в космическото пространство.
Дали само писателите са вярвали в такъв способ или и учените? През 1935 г. в България е публикувана статията на американския астроном Хенри Норис Ръсел "Възможно ли е отиването ни на Марс". Нека да дадем думата на автора:
"Няма нищо абсурдно в схващането на изстреляния снаряд, макар днешната балистика все още да не е в състояние да се справи с тази задача.
Кой е най-добрият начин за изстрелване на снаряд, който да може да достигне Марс или някоя друга планета? Как ще бъде извършено прицелването? Кога трябва да бъде изстрелян и каква начална скорост трябва да му бъде придадена?
Двете големи препятствия, както се знае, са земното притегляне и въздушното съпротивление. Нека за момент да се абстрахираме от тях и да се заемем с една по-проста задача. Да предположим, че обитаваме не нашата планета, а се намираме на малък астероид, който се движи около земната орбита. Разполагаме със средствата на днешната човешка техника и артилерия. Тъй като съпротивление на въздуха на практика отсъства, а гравитацията на малкото небесно тяло е твърде незначително, бихме ли могли да очакваме успех?
Ако пренебрегнем още и привличането на планетата, към която сме се прицелили, въпросът ще се опрости още повече, като се имат предвид законите за движението на планетите. Формулата за пресмятане скоростта на някое тяло – планета, астероид или снаряд – е лесна и си позволяваме да я дадем тук:

Тук V е скоростта по орбитата (относително Слънцето, разбира се), r – разстоянието на тялото от Слънцето, а - "средното отстояние" на тялото от Слънцето, тоест средното отстояние между най-голямото и най-малкото му отдалечаване от Слънцето по време на движението на това тяло около орбитата си. С е константа – а ко приемем разстоянието между Земята и Слънцето за мярка за a и r, а скоростите в км/сек, то С = 866 км. За Земята V = 29,76 км/сек. Нататък няма да взимаме предвид ексцентритета на земната орбита, но тази на Марс е твърде ексцентрична, за да бъде пренебрегната. Неговото средно отстояние от Слънцето е 1,524 (ако се вземе средното земно отстояние за единица), когато неговото действително отстояние се движи между 1,382 при перихелия до 1,664 в афелия.
Нашата формула дава за скоростта на Марс около орбитата му 26,50 км/сек при първото му положение и 21,95 км/сек при второто.
Ако, след като напусне астероида ни, изстреляният от нас снаряд се движи бавни по земния път, неговото средно отстояние по отношение на Слънцето ще бъде по-малко. По-голямата част от неговата орбита (макар и не изцяло) ще бъде отвъд земната, а това е най-сигурният начин, за да се прицелим в Марс. Очевидно, оръдието трябва да се насочи така, че снарядът да се движи по-бързо около Слънцето, отколкото самото то. Това ще се постигне най-добре, ако дулото на оръдието се насочи по посока на движението на планетата-стартова площадка около орбитата й. Така снарядът ще се движи на по-голямо средно отстояние в сравнение със Земята. Щом бъде изстрелян, той ще се ориентира под прав ъгъл спрямо посоката, съединяваща ни със Слънцето и ще бъде на разстояние 1 – следователно, целият му път ще лежи извън земната орбита.
Ако скоростта му бъде увеличена, орбитата му ще се отдалечава все повече и повече от Слънцето и накрая ще отиде по-далеч от Марс. Ще бъде по-добре, ако се подбере най-близката точка от орбитата на Марс (фиг. 1).

Най-голямото отдалечение на снаряда от Слънцето по неговата орбита и земята ще бъде равно на най-малкото отстояние на Марс. Средно то е равно на онова между Земята и Марс, тоест 1,191. От формулата следва, че по отношение на Слънцето снарядът ще се движи със скорост 31,80 км/сек при перихелия си. Тя е твърде висока, но само със 2,04 км/сек по-висока в сравнение със скоростта на Земята. Твърде лесно оръдието ще може да се насочи напред, по посока на еклиптиката, на 90 градуса западно от Слънцето, и ще се получи 94 % от исканата скорост – оръдието ще трябва да даде само малко повече от 6 %.
Ако се допусне грешка и оръдието бъде насочено в погрешна посока, ще е необходимо снарядът да има начална скорос 61,56 км /сек, или 30 пъти по-висока.
Но и в най-добрия случай минималната скорост от 2040 метра в секунда е достатъчно голяма. Според съобщенията, които се дадоха по време на войната (Първата световна война – бел. моя, А. О.) оръдието, с което германците бомбардираха Париж ("Дебелата Берта"), е давало на своите снаряди скорост, близка до тази.
Следователно, ако не бе земното притегляне и атмосферното съпротивление, с една малко усъвършенствана "Дебела Берта" ние бихме могли да "бомбардираме" Марс.
В афелия един такъв снаряд би имал скорост 2392 км/сек, а тази на Марс е с 2,59 км/сек по-висока. Поради това Марс ще го задмине, а за един марсианец би сметнал, че снарядът пада от небето по посока на планетата му.
Времето на летеж може да се определи по третия закон на Кеплер – 237 дни – или около 8 месеца. Отначало снарядът ще се движи по-бързо от Земята, но отдалечавайки се от Слънцето, той ще забавя движението си и накрая ще се движи по-бавно от Марс. Отначало, в момента на изстрела, снарядът ще се намира почти на една линия с Марс, но това няма да е така, ако целта е по-далечна – напр. Юпитер. Би било възможно срещата да стане в друга точка от марсианската орбита, ако се увеличи скоростта на снаряда. Пресметне ли се тя при тези случаи, ще се види, че за да се достигне афелият на Марс, снарядът трябва да има скорост 3,57 км/сек. Това би било една доста трудна задача за съвременната ни артилерия, но тогава снарядът би стигнал до Марс с относителна скорост 1,98 км/сек. Ако пък някой марсианец би желал да достигне по такъв начин Земята, ще направи най-добре да изстреля снаряда си наобратно, от афелия на своята планета, със същата скорост.
Но ако вземем под внимание привличането на Земята и това на Марс, нещата ще се развият по съвсем друг начин. Ако приемем, че липсва въздушно съпротивление, на снаряда ще бъде необходима начална скорост от 11,4 км/сек, за да може той да напусне повърхността на Земята. Дори и със съвсем малко да се превиши тази начална скорост, и проблеми с напускането на Земята снарядът няма да има. Например, повиши ли се тя само с 6,18 км, ще получим 2,04 км/сек на онова разстояние, за което говорихме вече (при това трябва да се вземе под внимание кинетичната енергия). Но на едно толкова бързо движещо се тяло атмосферата ще окаже неимоверно съпротивление, а последиците от това биха били твърде тежки. И без това необходимата скорост е много по-висока от онази, която би могла да се получи от някой уред от Земята, така че цялата работа засега остава в бъдещето.

Ако се върнем на нашия астероид, ще имаме неблагоприятна начална позиция за изстрел по Марс, защото на това разстояние той е само един малък диск. И една малка промяна в началната скорост би удължила орбитата на снаряда, така че Р4 би останало извън М4, планетата би преминала край снаряда, без да го срещне. Едно твърде просто пресмятане чрез нашата формула показва, че промяна в скоростта V с 1 см/сек ще отмести Р4 на 81 км.
Диаметърът на Марс е около 6700 км. Ако сега оръдието придаде на снаряда скорост в секунда, по-висока само с 45 см, той вероятно няма да улучи планетата, защото днешната балистика все още не е постигнала такава точност.
Доста интересно е, че за посоката на цевта необходимата точност не е така голяма. Едно слабо отклонение навън от Е0 ще принуди снаряда да се движи извън равнината по почти целия си път, но ще я пресече твърде близо до Р4, така че той ще удари Марс отзад. Същото би било, ако посоката на прицелването се промени в посока малко по-нагоре или по-долу – извън равнината на еклиптиката, предполагайки, че се намираме в нея. С това ще се предизвикат и много нови усложнения, за които не е мястото да говорим тук.
При всяка подобно пресмятане на траектория трябва да се вземат предвид още много неща – движението на оръдието поради земното въртене, привличането на Луната и другите планети, а специално и това на Марс в момента на падането на снаряда. А това би било една непосилна задача даже и в случай, че началното движение е точно определено.
В своя велик роман Хърбърт Уелс изстрелва десетки снаряди от Марс. За съжаление обаче трябва да кажем, че едва ли космически пътешественици в такъв снаряд биха достигнали Земята живи. За да се отделят от Марс, те трябва да получат скорост 5 км/сек, а за да достигнат Земята – 5,4 км/сек. За да се придаде тази скорост, при цев на оръдието с дължина 16 км е необходимо средно ускорение около сто пъти по-голямо от силата на земното притегляне. А такова едно ускорение веднага ще сплеска всяко същество, по-голямо от мравка, а даже и от микроб. Да не говорим за удара при сблъсъка със земната ос, който би бил ужасен.
Но безнадежно е почти живи същества да преминат някога междузвездното пространство. Наистина можем да си представим ракетни кораби, но техният успех е твърде съмнителен. Няма също и надежда, че живи същества биха преживели на някоя от другите планети. Но ако бъдещите кораби биха носили гориво колкото за един кръгов път, би било добре пилотът да следва пътя, който скицирахме тук."
Наистина интересно е да се види порочете песимистичното заключение на статията. Защото хората вече стигнаха до Луната. Със сигурност ще кацнат и на Марс!
Антон Оруш, Sandacite.net – www.sandacite.net
Източници:
Сп. Наука за всички, г. ІV, кн. 5 (януари 1935)
Сп. Природа, г. ХХІ, кн. 7 (март 1922)



















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон