
Днес е 14 март, "Денят на пи". Пи (π) е най-важната математическа константа и в нейна чест през 2009 г. Камарата на представителите на САЩ определя за неин празник този ден, който се пише 3.14 по американски маниер.
За по-голяма прецизност, може да отбележим празника точно в 1 часа и 59 минути, защото π≈3,14159.
Гръцката буква "π" изразява съотношението на обиколката на кръга и нейния диаметър.

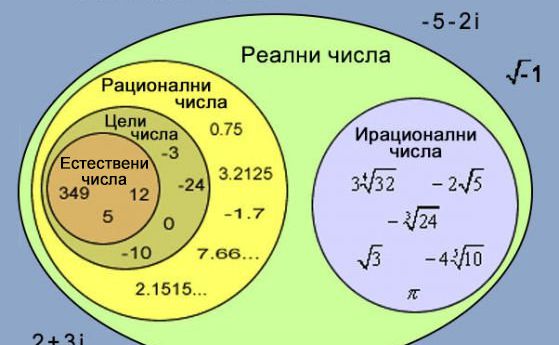
Пи e „ирационално число", защото не може да бъде записано като съотношение, като обикновена дроб. При ирационалните числа, цифрите след десетичната точка продължават безкрайно, без да се повтарят или да показват някаква периодичност. Числото π може да се изчислява хилядолетия, компютърни програми са определили милиарди цифри след запетайката и всяка следваща чифра е неизвестна.
π=3.1415926535897932384626433832795 (и още до безкрай)
Популярното приближение 22 / 7 = 3,1428571428571 ... е близко, но не точно.
Събрахме малко интересни факти за числото π:
- За първи буквата π - 16-ата буква от гръцката азбука е използвана през 1706 година от английския математик Уилям Джонс, за да се обозначи отношението на дължината на окръжността към нейния диаметър. Това обозначение става общоприето след публикуването на произведенията на Леонард Ойлер през 1737 г.

- Още самият Архимед се е опитвал да изчисли π. Легендата разказва, че заради това ученият е убит от римски войник. Персийският математик Ал-Хорезми (780г. - 850г.) е успял да намери първите четири цифри.
- Някои хора са посветили много години от своя живот за изчисляването на числото π. Например, холандският математик Лудолф ван Цейленг е прекарал десет години, за да изчисли числото π до 20 цифри след десетичната точка, Неговият резултат е публикуван през 1596. "Който има желание, да продължи"' - пише ученият в края на труда си. След смъртта му в неговите ръкописи са били открити още 15 цифри от числото. Намерените от него цифри на числото π са издълбани върху надгробния му камък. В чест на него понякога пи се нарича "лудолфово число". Да не забравяме, че това се случва през 17-ти век, когато всички изчисления се правят на ръка.
- Днес с помощта на суперкомпютри са изчислени 13 трилиона цифри след десетичната точка. В телевизионния сериал "Стар Трек" един от героите побеждава едил "зъл" компютър, като му задава да изчисли последната цифра на числото.
- В първия милион десетични цифри след десетичната точка комбинацията 12345 се появява повече от един път.
- Никой не знае дали древните египтяни са познавали числото π, но съотношението на височината на египетските пирамиди към периметъра е същото като отношението на дължината на окръжността към дължината на диаметъра.
- В щата Индиана през 1897 г. бил пуснат законопроект № 246, предложен от любителят математик Едуин Гудуин. Това е един от най-известните опити за налагане на научна истина със закон. Основната цел на законопроекта била да се създаде метод за квадратура на кръга, а не да налага определена стойност за константата π , законопроектът косвено установява няколко неправилни стойности на π , включително 3.2.
Предложението никога не става закон, благодарение на намесата на Кларънс A. Уолдо, професор по математика, случайно присъствал по време на дебата за закона.
Числото π участва в най-важните формули и уравнения на физиката:
- Принцип на неопределеността на Хайзенберг:
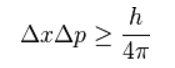
- Полевите уравнения на Айнщайн от Общата теория на относителността:
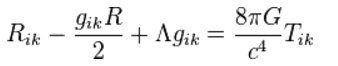
- Закон на Кулон за електрическата енергия:
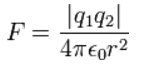





















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
15.03 2016 в 11:02
15.03 2016 в 08:47
Имаме 113355. След това се взима втората половина от полученото число за числител, а първата за знаменател и се получава 355/113. Това приближение съвпада с пи до седмия знак. По-добро приближение е било намерено едва 800 години по-късно.
Последни коментари
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон
dolivo
Сахара очаква 75% увеличение на валежите до 2100 г.
dolivo
Земната ябълка: стара култура за новите климатични времена
dolivo
Земята потъмнява. Какво означава тази тревожна климатична тенденция за бъдещето?
Nikor
На 30 септември 1928 е открит пеницилинът