Математици от Университета на Манчестър са отговорили на въпроса: Колко лотарийни билета трябва да купите, за да си гарантирате печалба в Националната лотария на Великобритания?
Фокусирайки се върху водещата игра на Националната лотария "Лото", която тегли шест случайни числа от 1 до 59, д-р Дейвид Стюарт (David Stewart) и д-р Дейвид Къшинг (David Cushing) установяват, че 27 е най-малкият възможен брой билети, необходими за гарантиране на печалба - макар и, което е важно, без гаранция за печалба.
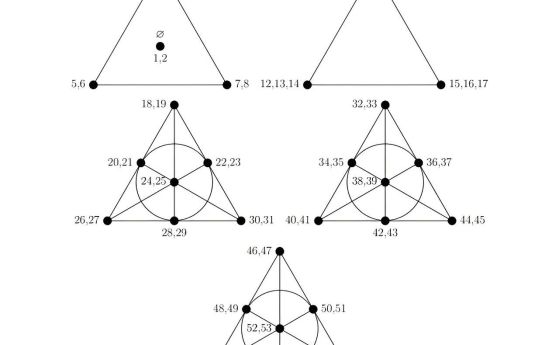
Те описват решението с помощта на математическа система, наречена крайна геометрия, която е фокусирана около триъгълна структура, наречена равнина на Фано. Всяка точка от структурата е начертана с двойки числа и е свързана с линии - всяка линия генерира набор от шест числа, което се равнява на един билет.
Необходими са три равнини на Фано и два триъгълника, за да се обхванат всички 59 числа и да се генерират 27 комплекта билети.
Избирането на билети по този начин гарантира, че независимо от това кое от 45 057 474 възможни тегления се случи, поне един от билетите ще има поне две съвпадащи числа. От всяко теглене на шест числа две трябва да се появят в една от петте геометрични структури, което гарантира, че те ще се появят поне в един билет.
Но д-р Стюарт и д-р Къшинг отбелязват, че всъщност работата им показва, че постигането на същия резултат с 26 билета е невъзможно.
27-те набора от числа на лотарийните билети. Кредит: University of Manchester
Д-р Дейвид Стюарт, преподавател по чиста математика в Университета в Манчестър, казва: "В основата си има противоречие, което идва от факта, че в 26 билета има само 156 резултата. Това означава, че много числа не могат да се появят многократно. В крайна сметка се вижда, че ще може да се намерят шест числа, които не се появяват на нито един билет едновременно. На езика на теорията на графите в крайна сметка доказваме съществуването на независимо множество с размер шест."
Въпреки че гарантира печалба, изследователите казват, че шансовете за реализиране на печалба са много малко вероятни и не трябва да се използват като причина за хазарт.
27-те лотарийни билета ще ви струват 54 паунда. А Питър Роулет, математик от уебсайта The Aperiodical, е показал, че в почти 99% от случаите няма да си върнете тези пари.
При изпробването на теорията в тегленето на лотарията на 1 юли 2023 г.; изследователите са уцелили само две топки на три от билетите, като наградата е била три опита за късмет при следваща лотария, всеки от които е останал без резултат.
Изследователите заявяват, че откритието е интересно от изчислителна гледна точка. Те използват петдесетгодишен език за програмиране, наречен Prolog, което според тях го прави един от най-старите примери за истински изкуствен интелект.
Източник: How many lottery tickets do you need to buy to guarantee a win? Mathematicians find the answer, University of Manchester
Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари