

–ē–ļ–ł–Ņ –ĺ—ā —É—á–Ķ–Ĺ–ł –ĺ–Ī—Ź–≤–ł, —á–Ķ –Ķ –Ņ–ĺ–Ľ—É—á–ł–Ľ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į –∑–į–ī–į—á–į –∑–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ –Ĺ–į¬†–Ņ–ł—ā–į–≥–ĺ—Ä–ĺ–≤–ł —ā—Ä–ĺ–Ļ–ļ–ł. –†–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ķ –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ–ĺ —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į —Ā—É–Ņ–Ķ—Ä–ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–į Stampede –≤ –£–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –Ĺ–į –ļ–į–Ľ–ł—Ą–ĺ—Ä–Ĺ–ł—Ź, –į –ĺ–Ī–Ķ–ľ—ä—ā –ľ—É –Ķ 200 —ā–Ķ—Ä–į–Ī–į–Ļ—ā–į.
–í –ļ–ĺ–ľ–Ņ—Ä–Ķ—Ā–ł—Ä–į–Ĺ–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ—ā–ĺ –∑–į–Ķ–ľ–į 68 –≥–ł–≥–į–Ī–į–Ļ—ā–į. –ó–į –ī–į —Ā–Ķ —Ä–į–∑–≥—ä—Ä–Ĺ–Ķ –į—Ä—Ö–ł–≤–į –ī–į–Ĺ–Ĺ–ł –ł –∑–į –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–į—ā–į –ł–ľ —Ā–į –Ĺ—É–∂–Ĺ–ł –ĺ–ļ–ĺ–Ľ–ĺ 30 000 —á–į—Ā–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ĺ –≤—Ä–Ķ–ľ–Ķ, –į –∑–į –ī–į —Ā–Ķ –Ņ—Ä–ĺ–≤–Ķ—Ä–ł –ĺ—ā —á–ĺ–≤–Ķ–ļ, –Ĺ–Ķ –Ī–ł –ľ—É —Ā—ā–ł–≥–Ĺ–į–Ľ —Ü—Ź–Ľ –∂–ł–≤–ĺ—ā —Ä–į–Ī–ĺ—ā–į, –ĺ—ā–Ī–Ķ–Ľ—Ź–∑–≤–į Nature.¬†
–Ę–ĺ–≤–į –Ĺ–Ķ –Ķ –Ņ—ä—Ä–≤–ĺ—ā–ĺ –Ņ–ĺ–ī–ĺ–Ī–Ĺ–ĺ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ - —Ā–Ķ–≥–į –ī–ĺ—Ā—ā–į –ĺ–Ī—Č–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–ł, –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ –≤ –ļ–ĺ–ľ–Ī–ł–Ĺ–į—ā–ĺ—Ä–ł–ļ–į—ā–į, —Ā–Ķ —Ä–Ķ—ą–į–≤–į—ā —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –ľ–ĺ—Č–Ĺ–ł –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–ł —Ā–ł—Ā—ā–Ķ–ľ–ł, —ā—ä–Ļ –ļ–į—ā–ĺ –Ĺ–Ķ —Ā–į –Ņ–ĺ —Ā–ł–Ľ–ł—ā–Ķ –Ĺ–į —á–ĺ–≤–Ķ–ļ.¬†
–ü—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā –Ĺ–į –Ď—É–Ľ–Ķ–≤–ł—ā–Ķ –Ņ–ł—ā–į–≥–ĺ—Ä–ĺ–≤–ł —ā—Ä–ĺ–Ļ–ļ–ł –∑–į–Ĺ–ł–ľ–į–≤–į –ī—ä–Ľ–≥–ł –≥–ĺ–ī–ł–Ĺ–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ. –ü—Ä–Ķ–∑ 1980 –≥. –Ķ –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–į –ĺ—ā –†–ĺ–Ĺ–į–Ľ–ī –ď—Ä–Ķ—ä–ľ –ī–ĺ—Ä–ł –Ņ–į—Ä–ł—á–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā¬†100 –ī–ĺ–Ľ–į—Ä–į –∑–į –≤—Ā–Ķ–ļ–ł, –ļ–ĺ–Ļ—ā–ĺ —Ä–Ķ—ą–ł –∑–į–ī–į—á–į. –°–į–ľ–ĺ –Ķ–ļ–ł–Ņ—ä—ā, –ļ–ĺ–Ļ—ā–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ, —Ā–Ľ–Ķ–ī –Ņ—Ä–ĺ–≤–Ķ—Ä–ļ–į,¬†¬† –Ņ–ĺ–Ľ—É—á–ł —Ā–ł–ľ–≤–ĺ–Ľ–ł—á–Ĺ–ĺ—ā–ĺ –≤—ä–∑–Ĺ–į–≥—Ä–į–∂–ī–Ķ–Ĺ–ł–Ķ.
–ó–į–ī–į—á–į—ā–į —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā —Ā–Ľ–Ķ–ī–Ĺ–ĺ—ā–ĺ. –í—ä–∑–ľ–ĺ–∂–Ŗ嬆–Ľ–ł –Ķ –ī–į —Ā–Ķ –ĺ—Ü–≤–Ķ—ā–ł –≤—Ā—Ź–ļ–ĺ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ –ł–Ľ–ł —Ā–ł–Ĺ—Ć–ĺ, —ā–į–ļ–į —á–Ķ —ā—Ä–ĺ–Ļ–ļ–į –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ł —á–ł—Ā–Ľ–į a, b –ł c, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź–≤–į—Č–ł –ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į, a2 + b2 = c2¬†–ī–į –Ĺ–Ķ —Ā–į –Ī–ĺ—Ź–ī–ł—Ā–į–Ĺ–ł –≤ –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł —Ü–≤—Ź—ā.
–Ě–į–Ņ—Ä–ł–ľ–Ķ—Ä, –ī–į —Ä–į–∑–≥–Ľ–Ķ–ī–į–ľ–Ķ –ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–į—ā–į —ā—Ä–ĺ–Ļ–ļ–į 3,¬†4 –ł 5. –ź–ļ–ĺ 3 –ł 5 —Ā–į ‚Äč‚Äč–ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł –≤ —Ā–ł–Ĺ—Ć–ĺ, —ā–ĺ —á–ł—Ā–Ľ–ĺ—ā–ĺ 4 —ā—Ä—Ź–Ī–≤–į –∑–į–ī—ä–Ľ–∂–ł—ā–Ķ–Ľ–Ĺ–ĺ –ī–į –Ķ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ĺ –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ.
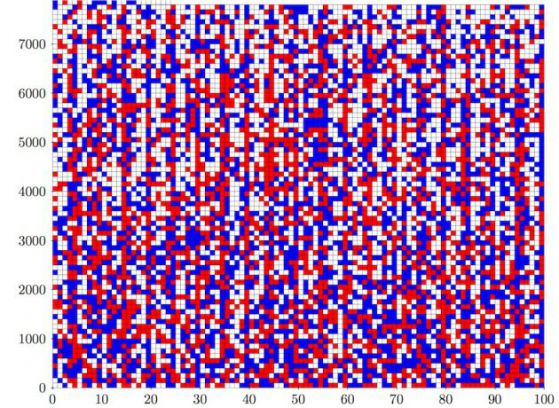 –ß–ł—Ā–Ľ–į—ā–į –ĺ—ā 1 –ī–ĺ 7824 –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł –ł–Ľ–ł –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ –ł–Ľ–ł —Ā–ł–Ĺ—Ć–ĺ, —ā–į–ļ–į —á–Ķ —ā—Ä–ĺ–Ļ–ļ–į—ā–į a, b –ł c, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź–≤–į—Č–į –ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į, a2 + b2 = c2¬†–ī–į –Ĺ–Ķ –Ķ –Ķ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–į –≤ –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł —Ü–≤—Ź—ā. –†–Ķ—ą–Ķ—ā–ļ–į—ā–į –ĺ—ā 7,824 –ļ–≤–į–ī—Ä–į—ā—á–Ķ—ā–į —ā—É–ļ –Ņ–ĺ–ļ–į–∑–≤–į –Ķ–ī–Ĺ–ĺ —ā–į–ļ–ĺ–≤–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ, —Ā —á–ł—Ā–Ľ–į, –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ –ł–Ľ–ł —Ā–ł–Ĺ—Ć–ĺ (–Ī–Ķ–Ľ–ł—ā–Ķ –ļ–≤–į–ī—Ä–į—ā–ł –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–į—ā –ł –Ķ–ī–ł–Ĺ–ł—Ź—ā, –ł –ī—Ä—É–≥–ł—Ź—ā —Ü–≤—Ź—ā).¬†
–ß–ł—Ā–Ľ–į—ā–į –ĺ—ā 1 –ī–ĺ 7824 –ľ–ĺ–≥–į—ā –ī–į –Ī—ä–ī–į—ā –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł –ł–Ľ–ł –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ –ł–Ľ–ł —Ā–ł–Ĺ—Ć–ĺ, —ā–į–ļ–į —á–Ķ —ā—Ä–ĺ–Ļ–ļ–į—ā–į a, b –ł c, —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź–≤–į—Č–į –ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–į—ā–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į, a2 + b2 = c2¬†–ī–į –Ĺ–Ķ –Ķ –Ķ –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–į –≤ –Ķ–ī–ł–Ĺ –ł —Ā—ä—Č–ł —Ü–≤—Ź—ā. –†–Ķ—ą–Ķ—ā–ļ–į—ā–į –ĺ—ā 7,824 –ļ–≤–į–ī—Ä–į—ā—á–Ķ—ā–į —ā—É–ļ –Ņ–ĺ–ļ–į–∑–≤–į –Ķ–ī–Ĺ–ĺ —ā–į–ļ–ĺ–≤–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ, —Ā —á–ł—Ā–Ľ–į, –ĺ—Ü–≤–Ķ—ā–Ķ–Ĺ–ł –≤ —á–Ķ—Ä–≤–Ķ–Ĺ–ĺ –ł–Ľ–ł —Ā–ł–Ĺ—Ć–ĺ (–Ī–Ķ–Ľ–ł—ā–Ķ –ļ–≤–į–ī—Ä–į—ā–ł –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–į—ā –ł –Ķ–ī–ł–Ĺ–ł—Ź—ā, –ł –ī—Ä—É–≥–ł—Ź—ā —Ü–≤—Ź—ā).¬†
–í –ī–ĺ–ļ–Ľ–į–ī, –Ņ—É–Ī–Ľ–ł–ļ—É–≤–į–Ĺ –Ĺ–į —Ā—ä—Ä–≤—ä—Ä–į arXiv –Ĺ–į 3 –ľ–į–Ļ, —É—á–Ķ–Ĺ–ł—ā–Ķ –Ņ–ĺ–ļ–į–∑–≤–į—ā, —á–Ķ –ī–ĺ 7824 –≤—Ā–ł—á–ļ–ł –Ņ–ł—ā–į–≥–ĺ—Ä–ĺ–≤–ł —ā—Ä–ĺ–Ļ–ļ–ł —É–ī–ĺ–≤–Ľ–Ķ—ā–≤–ĺ—Ä—Ź–≤–į—ā —É—Ā–Ľ–ĺ–≤–ł—Ź—ā–į –Ĺ–į –∑–į–ī–į—á–į—ā–į. –ě—ā —á–ł—Ā–Ľ–ĺ—ā–ĺ –Ĺ–į—ā–į—ā—ä–ļ 7825 —ā–ĺ–≤–į –Ķ –≤–Ķ—á–Ķ –Ĺ–Ķ–≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ. –ė–ľ–į 102300 –Ĺ–į—á–ł–Ĺ–ł –∑–į –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ –Ĺ–į —ā—Ä–ĺ–Ļ–ļ–ł—ā–Ķ –≤ —Ä–į–∑–Ľ–ł—á–Ķ–Ĺ —Ü–Ķ—Ź—ā –ī–ĺ —á–ł—Ā–Ľ–ĺ—ā–ĺ 7825. –ó–į –ī–į –ī–ĺ–Ļ–ī–į—ā –ī–ĺ —ā–ĺ–≤–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ, –ł–∑—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–ł—ā–Ķ –ł–∑–Ņ–ĺ–Ľ–∑–≤–į—ā 2 –ī–Ĺ–ł —Ä–į–Ī–ĺ—ā–į –Ĺ–į —Ā—É–Ņ–Ķ—Ä–ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–į Stampede, –ļ–ĺ–Ļ—ā–ĺ –ł–ľ–į 800 –Ņ—Ä–ĺ—Ü–Ķ—Ā–ĺ—Ä–į. –ü–ĺ—Ā–Ľ–Ķ —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ķ –Ņ—Ä–ĺ–≤–Ķ—Ä–Ķ–Ĺ–ĺ —Ā –ī—Ä—É–≥–į –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä–Ĺ–į –Ņ—Ä–ĺ–≥—Ä–į–ľ–į.¬†
–ü—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā –Ĺ–į –ü–ł—ā–į–≥–ĺ—Ä–ĺ–≤–ł—ā–Ķ —ā—Ä–ĺ–Ļ–ļ–ł –Ķ —á–į—Ā—ā –ĺ—ā —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –†–į–ľ–∑–ł. –Ę—Ź –Ķ –ļ–Ľ–ĺ–Ĺ –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į, –ļ–ĺ–Ļ—ā–ĺ –ł–∑—É—á–į–≤–į —É—Ā–Ľ–ĺ–≤–ł—Ź—ā–į, –Ņ—Ä–ł –ļ–ĺ–ł—ā–ĺ —Ā–Ľ—É—á–į–Ļ–Ĺ–ĺ –≥–Ķ–Ĺ–Ķ—Ä–ł—Ä–į–Ĺ–ł –≥–ĺ–Ľ–Ķ–ľ–ł –Ĺ–į–Ī–ĺ—Ä–ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ĺ–Ī–Ķ–ļ—ā–ł –Ņ—Ä–ĺ—Ź–≤—Ź–≤–į—ā –Ņ–ĺ–ī—Ä–Ķ–ī–Ķ–Ĺ–ł —Ā—ā—Ä—É–ļ—ā—É—Ä–ł.
–ó–į–ī–į—á–ł—ā–Ķ –≤ —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –†–į–ľ–∑–ł¬†–ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ĺ —Ā–į –Ņ–ĺ–ī —Ą–ĺ—Ä–ľ–į—ā–į –Ĺ–į –≤—ä–Ņ—Ä–ĺ—Ā "–ļ–ĺ–Ľ–ļ–ĺ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į —ā—Ä—Ź–Ī–≤–į –ī–į –ł–ľ–į –Ĺ—Ź–ļ–į–ļ—ä–≤ –ĺ–Ī–Ķ–ļ—ā, –ļ–ĺ–Ķ—ā–ĺ –ī–į –≥–į—Ä–į–Ĺ—ā–ł—Ä–į –ī–į —Ā–Ķ –ł–∑–Ņ—ä–Ľ–Ĺ–ł –Ņ—Ä–Ķ–ī–≤–į—Ä–ł—ā–Ķ–Ľ–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ł–Ľ–ł —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –Ņ—Ä–Ķ–ī–≤–į—Ä–ł—ā–Ķ–Ľ–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ –ľ–ĺ–ī–Ķ–Ľ.
–Ě–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ –ĺ—ā —Ą–į–ļ—ā–į, —á–Ķ –ļ–ĺ–ľ–Ņ—é—ā—ä—Ä—ä—ā –Ķ —Ä–Ķ—ą–ł–Ľ –Ņ—Ä–ĺ–Ī–Ľ–Ķ–ľ–į, —ā–ĺ–Ļ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –ī–į–ī–Ķ –ĺ—ā–≥–ĺ–≤–ĺ—Ä –Ĺ–į –≤—ä–Ņ—Ä–ĺ—Ā–į –∑–į—Č–ĺ —á–ł—Ā–Ľ–ĺ—ā–ĺ 7825 –Ķ —ā–ĺ–Ľ–ļ–ĺ–≤–į —Ā–Ņ–Ķ—Ü–ł–į–Ľ–Ĺ–ĺ –ł–Ľ–ł –∑–į—Č–ĺ –ĺ—Ü–≤–Ķ—ā—Ź–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į —ā—Ä–ĺ–Ļ–ļ–ł—ā–Ķ –Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ –≤ —Ä–į–∑–Ľ–ł—á–Ĺ–ł —Ü–≤–Ķ—ā–ĺ–≤–Ķ.
–ú–į—ą–ł–Ĺ–ł—ā–Ķ –Ĺ–Ķ –ľ–ĺ–≥–į—ā –ī–į –ī–į–≤–į—ā —ā–į–ļ–ł–≤–į –ĺ—ā–≥–ĺ–≤–ĺ—Ä–ł, —ā–Ķ –ľ–ĺ–≥–į—ā –ī–į –ļ–į–∂–į—ā —Ā–į–ľ–ĺ –ī–į–Ľ–ł –Ķ –≤—Ź—Ä–Ĺ–ĺ. –∑–į—Ā–Ķ–≥–į –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ —Ā–į –Ĺ–Ķ–∑–į–ľ–Ķ–Ĺ–ł–ľ–ł.
–ě—Č–Ķ –Ņ–ĺ —ā–Ķ–ľ–į—ā–į
–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–Ě–ĺ–≤–ĺ –ĺ—Ä–ł–≥–ł–Ĺ–į–Ľ–Ĺ–ĺ –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –Ĺ–į —ā–Ķ–ĺ—Ä–Ķ–ľ–į—ā–į –Ĺ–į –ü–ł—ā–į–≥–ĺ—Ä

–§–ł–∑–ł–ļ–į
–ú—É–∑–ł–ļ–į—ā–į –Ĺ–į –í—Ā–Ķ–Ľ–Ķ–Ĺ–į—ā–į. –Ę–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į —Ā—ā—Ä—É–Ĺ–ł—ā–Ķ

–ú–į—ā–Ķ–ľ–į—ā–ł–ļ–į
–ö–ĺ–Ľ–ļ–ĺ –ļ—Ä–į—Ā–ł–≤–į –ľ–ĺ–∂–Ķ –ī–į –Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į (–ł–Ĺ—ā–Ķ—Ä–≤—é —Ā –í–Ľ–į–ī–ł–ľ–ł—Ä –°–ĺ—ā–ł—Ä–ĺ–≤)





















–ö–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
–ú–ĺ–Ľ—Ź, —Ä–Ķ–≥–ł—Ā—ā—Ä–ł—Ä–į–Ļ—ā–Ķ —Ā–Ķ –ĺ—ā T–£–ö!
–ź–ļ–ĺ –≤–Ķ—á–Ķ –ł–ľ–į—ā–Ķ —Ä–Ķ–≥–ł—Ā—ā—Ä–į—Ü–ł—Ź, –Ĺ–į—ā–ł—Ā–Ĺ–Ķ—ā–Ķ –Ę–£–ö!
–Ě—Ź–ľ–į –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł –ļ—ä–ľ —ā–į–∑–ł –Ĺ–ĺ–≤–ł–Ĺ–į !
–ü–ĺ—Ā–Ľ–Ķ–ī–Ĺ–ł –ļ–ĺ–ľ–Ķ–Ĺ—ā–į—Ä–ł
YKoshev
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Johnny B Goode
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
Gunteer
–ü—Ä–Ķ—Ā—ā–ł–∂–Ĺ–į –Ĺ–į–≥—Ä–į–ī–į –ĺ—ā –Ď–ź–Ě —Ā–Ņ–Ķ—á–Ķ–Ľ–ł –≥–Ľ–į–≤–Ĺ–ł—Ź—ā —Ä–Ķ–ī–į–ļ—ā–ĺ—Ä –Ĺ–į –Ě–į—É–ļ–įOFFNews
–•—Ä–ł—Ā—ā–ł—Ź–Ĺ–ł–Ĺ
–Ę–ĺ–≤–į –Ķ –ļ—Ä–į–Ľ—Ź—ā –Ĺ–į —ā–ł–ļ–≤–ł—ā–Ķ: –Ę–ł–ļ–≤–į—ā–į –ľ—É —ā–Ķ–∂–ł –Ĺ–į–ī –Ķ–ī–ł–Ĺ –Ķ–ī–ł–Ĺ —ā–ĺ–Ĺ