

Според великия немски математик Карл Фридрих Гаус: "Математиката е кралицата на науките, а аритметиката е кралицата на математиката". Съвременното наименование на клона на математиката, който Гаус нарича аритметика, е "Теория на числата" - изследване на свойствата на целите числа. Математикът от 19-ти век Кронекер казва, че "Бог е направил целите числа, всичко останало е дело на човека".
Основните градивни елементи на теорията на числата са простите числа. Това са числата: 2, 3, 5, 7, 11, 13,... дефинирани като цели числа, които не могат да бъдат разложени точно на друго цяло число, с изключение на тривиалното деление на числото 1.
Простите числа не могат да бъдат разложени на по-прости компоненти - те играят роля в математиката, подобна на ролята на елементите в химията. От около 100 химически елемента е възможно да се синтезират милиони съединения, които се изучават от химиците. Основната теорема на аритметиката, която е доказана от Евклид, гласи:
Всички положителни цели числа са или прости, или могат да бъдат уникално разложени на произведение от прости числа.
Например:

Ако вземем всички прости числа под 300, ще открием, че има само 62 от тях:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29,
31, 37, 41, 43, 47, 53, 59, 61, 67, 71
, 73, 79, 83, 89, 97, 101 , 103, 107, 109, 113,
127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179,
181, 191, 193, 197, 199, 211, 223, 227, 229,
2 33 , 239, 241, 251, 257, 263, 269, 271, 277, 281,
283, 293.
25 от тези прости числа са под 100, 21 са между 100 и 200 и 16 са между 200 и 300. Изглежда, че простите числа се разреждат все повече с увеличаването на стойността им. Ако погледнем по-нататък, ще открием, че между 10 000 и 10 100 има само 11 прости числа, между 100 000 и 100 100 има само 6.
Това потвърждава, че простите числа стават все по-редки, когато стават все по-големи, но дали в крайна сметка ще изчезнат напълно? Знаем, че на Земята няма естествено срещащи се елементи над номер 92 – уран.
Но вярно ли е същото и за простите числа? Кое е най-голямото просто число?
Няма най-голямо просто число
Свойствата на простите числа са изучавани от математиците от древността. Древните гърци първи доказват, че има безкрайно много прости числа, така че всъщност няма най-голямо просто число.
Евклид в "Елементи" представя най-старото известно доказателство. Доказателството показва, че ако приемем, че има най-голямо просто число, възниква противоречие. Можем да номерираме всички прости числа във възходящ ред, така че P1=2, P2=3, P3=5 т.н. Ако приемем, че има само n прости числа, тогава най-голямото просто число ще бъде обозначено като Pn. Сега можем да образуваме числото, Q като умножим всички тези прости числа и добавим 1, така че
Q = (P1 х P2 х P3 х P4... х Pn) + 1
Сега можем да видим, че ако разделим Q на някое от нашите n прости числа, винаги има остатък от 1, така че Q не се дели на нито едно от простите числа. Но знаем, че всички положителни числа са или прости, или могат да бъдат разложени на произведение на прости числа. Това означава, че или Q трябва да бъде просто, или Q трябва да се дели на прости числа, които са по-големи от Pn. Нашето предположение, че Pn е най-голямото просто число, ни доведе до противоречие, следователно това предположение трябва да е невярно, така че няма най-голямо просто число.
Как се разпределят простите числа?
Сега знаем, че простите числа стават по-редки, когато стават по-големи, но не намаляват напълно. Следващият въпрос е можем ли да разберем как са разпределени простите числа? Могат ли простите числа да следват някаква закономерност по начина, по който елементите могат да бъдат организирани в периодичната таблица? Това е един от най-важните проблеми в цялата математика.
Разстоянието между простите числа изглежда доста неравномерно, но изглежда има тенденция разстоянието да се увеличава, както отбелязахме по-горе. Теоремата за прости числа гласи, че функцията x/ln(x), където ln(x) е натурален логаритъм от x, дава разумно приближение за броя на простите числа, по-малък от x, който ще представим като Pi (x). С нарастването на x това приближение става все по-точно. Следната таблица сравнява тези две функции:
| х | Pi( x ) | x /ln( x ) | Pi( x )/( x ln( x )) |
| 1000 | 168 | 145 | 1,159 |
| 10 000 | 1,229 | 1086 | 1.132 |
| 100 000 | 9,592 | 8,686 | 1.104 |
| 1 000 000 | 78,498 | 72,382 | 1,084 |
| 10 000 000 | 664,579 | 620,420 | 1,071 |
| 100 000 000 | 5,761,455 | 5,428,681 | 1,061 |
Няма проста формула, която да генерира всички прости числа, но Ойлер показа, че формулата:
ƒ(n) = n² - n + 41
е забележително, защото е равно на просто число за всяка стойност на цяло число n до 40. Простите числа, генерирани от формулата, са:
41, 43, 47, 53, 61, 71, 83, 97, 113, 131, 151,
173, 197, 223, 251, 281, 313, 347, 383, 421, 461, 503,
547, 593, 641, 691, 743, 797, 853, 911,
971, 1033, 1097, 1163, 1231, 1301, 1373, 1447, 1523, 1601.
Формулата по необходимост не успява да произведе просто, когато n = 41, защото в този случай ƒ(n) = n²=41²
Ойлер измисля и една много по-важна функция, която сега е известна като дзета функция:
ζ (s) = Σ (1/ns) = 1-s + 2-s + 3-s + 4-s + ...
Ойлер показа, че дзета функцията е равна на безкрайно произведение:

където произведението е върху всички прости числа p. Това е забележителен резултат: когато дзета функцията е изразена като сума от безкраен брой членове, сумата включва член, който приема стойност за всяко положително цяло число, но когато е изразена като безкрално произведение, единствените включени членове са тези, които приемат стойност за просто число.
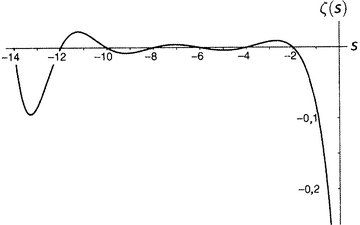
Дзета функцията, както е дефинирана от Ойлер, е валидна само за стойности s, които са по-големи от 1. За тези стойности на s дзета функцията може да се сумира до крайна стойност, въпреки че броят на членовете е безкраен. Но ако s е равно или по-малко от 1, редът е разходящ, така че функцията не е добре дефинирана. Например за s = -2 дава
Σ(1/n-2) = Σn2 = 1 + 4 + 9 + 16 + ....
ред, който се увеличава безкрайно. За сравнение, когато s = -2,
ζ (2) = Σ (1/n2) = 1-2 + 2-2 + 3-2 + 4-2 + ... = 1 + 1/4 + 1/9 + 1/16 + ...
Резултатите, които се получават, ще бъдат все по-близки до числото π2/6=1.644934..., но никога няма да го надскочат. Казано по математически: редът клони към π2/6, или сумата на реда е равна на π2/6.
Установихме до тук, че за всяко s > 1 редът на Ойлер е сходящ.
Продължение на дзета-функцията на Ойлер
Излезе, че разглежданата дзета-функция на Ойлер ζ (s) е определена за реални числа x по-големи от 1. Реалните числа са част от по-голяма група числа, наречени комплексни числа. И докато реалните числа съответстват на всички точки на числовата ос, комплексните числа съответстват на всички точки на равнината, съдържаща реалната числова права. Тази равнина се нарича комплексна равнина. И точно както функцията се определя от аргументи, които са реални числа, точно така може да дефинираме функцията като аргументи са й комплексни числа.
Един интересен факт, свързан с функциите на комплексните променливи е, че ако знаете стойностите на функцията за някакво множество данни, то може да се научат стойностите на функцията във всяка точка в комплексната равнина.
Този метод за разширяване на областта на функцията е известен като аналитично продължение. Дзета-функцията на Ойлер е определена за реални числа по-големи от 1. Тъй като реалните числа са частен случай на комплексни числа, можем да считаме тази функция като комплексна функция, а след това да използваме аналитичното продължаване, за да получим нова функция, дефинирана за цялата равнина, но съгласувана с дзета функцията на Ойлер за реални числа по-големи от 1.
Дзета функцията на Риман
Риман разбира, че дзета функцията е ключът към теоремата за разпределението на простите числа, но за да се приложи този подход, трябва да се разшири, да се определи дзета функцията не само за реални, но и за комплексни променливи.
Има още едно нещо, което може да се направи. С помощта на комплексния математичен анализ, може да се разшири областта на определение на дзета-функцията на Ойлер така, че за числа по-малки или равни на 1 функцията да приема крайни стойности. С други думи, има начин да се определи нова функция, която ще наречем ζ (x) :
ζ(x) = 1/1x + 1/2x + 1/3x + 1/4x + … .
За x > 1 и за x < 1 функцията ζ(x) ще приема определени крайни стойности. Този метод се нарича аналитично продължение и новата функция, която се получава, се нарича дзета-функцията на Риман. Създаването на тази нова функция приемаща крайни стойности и за x < 1 се състои в изваждането от несходящия ред на друг несходящ ред. Така от безкрайността, получаваща се от първата разходяща сума минус безкрайността, която дава втората разходяща сума, се получава нещо крайно.
Риман разширява определението на ζ (x) за всички комплексни числа освен 1. Единицата е изключена, защото за x = 1, стойността на дзета-функцията става безкрайна.
Интуицията на Риман е доста забележителна при свързването на свойствата на непрекъсната функция на комплексна променлива със свойствата на простите числа, които са реални и дискретни. По-конкретно, Риман показва, че броят на простите числа, по-малки от x, е свързан с точките, в които дзета функцията е равна на нула - тези точки са известни като нули на функцията.
Тривиални и нетривиални нули
Риман успял да покаже, че разпределението на простите числа зависи от това къде дзета-функцията се нулира. Тя има така наречените тривиални нули в четните отрицателни числа (–2, –4, –6, …). Те са тривиални в смисъл, че тяхното съществуване може да се докаже сравнително лесно (например използвайки функционалното уравнение).
Всички останали нули се наричат нетривиални. Задачата се състои в това, да се опишат всички останали нули на дзета-функцията. А всички нетривиални нули на дзета-функцията се получават за комплексни числа. Те лежат на критичната линия, а реалната им част, равна на 1/2.
Това е и забележителната хипотеза на Риман.
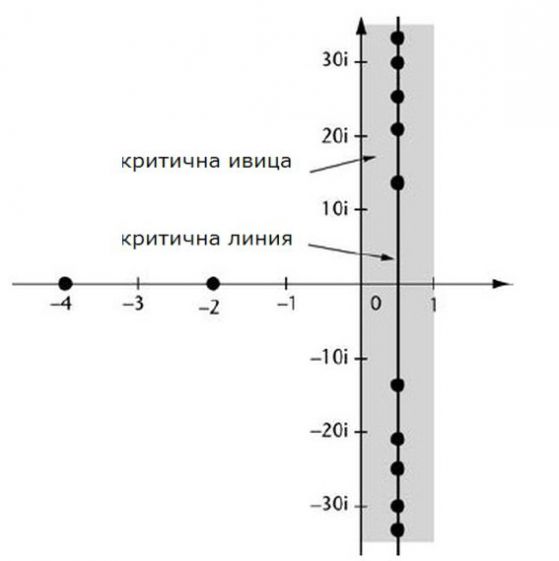
Нулите на дзета-функцията, критичната линия и критичната ивица
Хипотезата става известна като хипотезата на Риман и е ключът към разбирането на разпределението на простите числа и все още няма доказателство, че няма изключения от този модел.
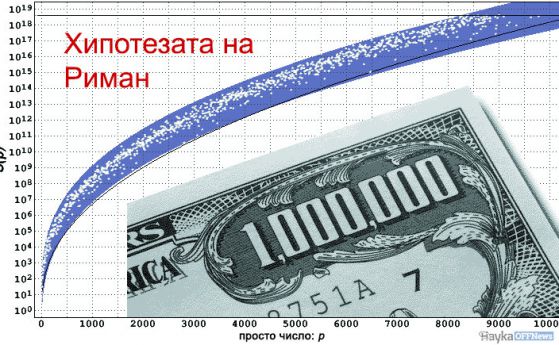
Коя е най-трудната задача в цялата математика?
Доказателството на хипотезата на Риман е проблемът, който вече 150 години измъчва най-талантливите математици на Земята. Местоположението на нулите на дзета-функцията е от огромна важност за теорията на числата. Информацията за нетривиалните нули дава отговори и на други въпроси извън математиката.
Никой досега не я е доказал, но малцина са тези, които се съмняват, че хипотезата на Риман е вярна. Числените експерименти са повече от убедителни - вече са изчислени първите 1013 нули на Римановата дзета-функция и строго е установено, че повече от 40% от нулите на дзета-функции удовлетворяват хипотезата.
От друга страна последната теорема на Ферма е постигнала легендарен статут сред математиците, защото през 17-ти век френският държавен служител и аматьор математик Пиер дьо Ферма, една от най-великите фигури в историята на теорията на числата, е надраскал в полето на книга, че е имал чудесно доказателство на теоремата, но полето е твърде малко, за да го запише. Книгата е издание от 17-ти век на класическия гръцки текст за Теория на числата, написан през първи век от новата ера, Аритметика на Диофант. Впоследствие Ферма умира, оставяйки математиците да търсят 350 години доказателство на теоремата.
През 150-те години от статията на Риман никой никога не е успял да докаже или отхвърли предположението му, но последната теорема на Ферма най-накрая е доказана от Андрю Уайлс през 1994 г.
Хипотезата на Риман сега е най-известната изключителна задача в математиката. Но хипотезата на Риман има много по-важни последствия за математиката от последната теорема на Ферма.
Всъщност има области на математиката, които са разработени от математиците въз основа на предположението, че хипотезата на Риман е вярна. Хипотезата на Риман също изглежда дори по-трудна задача от последната теорема на Ферма.
Спиралата на простите числа на Улам
Всяка неявна закономерност в простите числа, която е кодирана в дзета функцията, все още не е изрично дешифрирана. Въпреки това, има много по-прост модел, показан в разпределението на прости числа.
През 1963 г. полският математик Станислав Улам, който работи върху американската ядрена програма, проекта Манхатън, по време на Втората световна война, рисува абстрактно в паузата между два семинара на конференция.
Той начертава матрица от квадрати, след това написва числото 1 в центъра на мрежата и продължава да изписва последователността от всички положителни числа във възходящ ред, излизащи спираловидно от центъра. Улам забелязва за своя голяма изненада, че когато целите числа са организирани по този начин, има тенденция простите числа да се подреждат по диагонални линии в матрицата.
Резултатът е толкова неочакван, че снимка на спиралата на простите числа е представена на корицата на изданието от март 1964 г. на Scientific American, което включва статия от Мартин Гарднър за спиралата: "Математически развлечения: Забележителното знание за простото число". Sci. амер. 210, 120-128, март 1964 г.
 Спиралата на простите числа на Улам
Спиралата на простите числа на Улам
Илюстрацията по-горе показва спиралата за първите 100 000 цели числа. Съставните числа са показани като черни точки, а простите числа са показани като бели точки. В решетката ясно се виждат множество дълги диагонални бели линии. Ако за начално число на спиралата се вземат числа, различни от 1, общият вид на матрицата е същият. Никой не е дал ясно обяснение защо това трябва да е така. Но това предполага, че има дълги поредици от прости числа, които могат да бъдат генерирани от формули като f ( n )= an 2 + bn + c , където a, b и c са цели числа.
Ако започнем с числото 41 в центъра на спиралата, ще открием, че числата по диагонала образуват последователността f ( n )= n 2 - n +41, което е формулата, открита от Ойлер, която дава като стойности прости числа за всички цели числа от n до 40.
На илюстрацията по-долу числото 41 е разположено в центъра и числата продължават в спирала, обратна на часовниковата стрелка. Квадратите на матрицата, които съдържат съставни числа, са оцветени в жълто, а квадратите, които съдържат прости числа, са оцветени в бяло. Първите 15 числа, генерирани по формулата:
ƒ ( n )= n 2 - n +41, се появяват по един от главните диагонали на квадрата.
 Простите числа (в бяло) са разположени по диагонала на спиралата
Простите числа (в бяло) са разположени по диагонала на спиралата
Въпреки че Станислав Улам обикновено се смята за откриването на спиралата на простите числа, изглежда, че Улам може да не е първият човек, направил това откритие. Глава 6 от класическия роман на Артър К. Кларк от 1956 г. "Градът и звездите" започва с героя Йезерак, който анализира "водовъртеж" от цели числа на компютърния си монитор и вижда простите числа, нанизани "по повърхността му като мъниста, които могат да бъдат подредени на пресечните точки на мрежа". Изглежда, че Артър Кларк вече е открил спиралата на простите числа седем години преди да бъде открита от Улам.
Водовъртеж от числа
Математиците изучават свойствата на простите числа за свой собствен присъщ интерес. Но простите числа имат и модерни научни приложения, особено в криптографията.
Правителствената разузнавателна агенция на Съединените щати, NSA, е най-големият работодател в света на чистата математика.
Всеки път, когато правите транзакция в интернет, като например покупка с кредитна карта, сигурността на транзакцията се гарантира чрез използването на криптиране с публичен ключ, като се използва метод, базиран на някаква фина теория на числата, създадена от Рон Ривест, Ади Шамир и Лен Адлеман, известен също като RSA.
RSA криптирането използва цифров ключ, който се формира чрез умножаване заедно на две много големи прости числа. Сигурността на системата зависи от трудността на факторизирането (разлагането на множители) на много големи числа. Броят на стъпките, които са необходими за факторизиране на голямо число с помощта на всички известни алгоритми, нараства експоненциално с размера на числото.
Това означава, че криптографът винаги може да бъде една крачка пред компютъра. Ако компютърните процесори станат достатъчно бързи, за да факторизират 128-цифрените числа, които се използват за шифроване, можем да започнем да използваме 512-цифрени числа. Въпреки това, ако някой математик намери нов по-ефективен алгоритъм за факторизация, сигурността на нашите шифровани транзакции може да бъде застрашена. Криптографите се чувстват сигурни, защото въпреки че водещи математици са търсили такъв алгоритъм в продължение на много векове, никой никога не е бил намерен.
Но трима индийски математици – проф. Маниндра Агравал (Manindra Agrawal) и двама от неговите аспиранти, Нирадж Каял и Нитин Саксена (Neeraj Kayal and Nitin Saxena) – са публикували алгоритъм за тестване дали едно число е просто или съставно. Алгоритъмът използва доста елементарна аритметика и е изложен от авторите само в 13 реда. Важната нова характеристика на алгоритъма е, че времето, необходимо за проверка дали числото N е просто, нараства полиномно с размера на N, а не експоненциално. Всъщност времетото нараства като дванадесета степен на N.
 След това откритие, може би не трябва да бързаме да изключим възможността, че може да има и прост алгоритъм за разлагане на множители, който също е бил пренебрегнат.
След това откритие, може би не трябва да бързаме да изключим възможността, че може да има и прост алгоритъм за разлагане на множители, който също е бил пренебрегнат.
Наскоро изследователи от Градския университет в Хонконг (CityUHK) и Държавния университет на Северна Каролина, САЩ, заявиха, че простите числа могат да бъдат предвидени. Резултатът от изследването на екипа е удобна периодична таблица на простите числа, посочваща местоположенията на простите числа.
Авторът на статията Никълъс Мий (Nicholas Mee) е учил математика в университета в Кеймбридж, бил е Senior Wrangler през 1985 г. и е защитил докторска степен с дисертация със заглавие "Суперсиметрична квантова механика и геометрия".
Източник: A whirlpool of numbers, Plus maths magazine





















Коментари
Моля, регистрирайте се от TУК!
Ако вече имате регистрация, натиснете ТУК!
Няма коментари към тази новина !
Последни коментари
YKoshev
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Johnny B Goode
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Gunteer
Престижна награда от БАН спечели главният редактор на НаукаOFFNews
Християнин
Това е кралят на тиквите: Тиквата му тежи над един един тон